2) College of Marine Geosciences, Ocean University of China, Qingdao 266100, China;
3) Marine Ecological Restoration and Smart Ocean Engineering Research Center of Hebei Province, Qinhuangdao 066000, China
A submarine landslide is a common marine geological disaster that occurs worldwide. It threatens the safe operation of marine infrastructure such as offshore wind turbines, drilling platforms, submarine pipelines, and cables due to its characteristics of large volume, high speed, and long runout distance (Rzadkiewicz et al., 1997; Perez-Gruszkiewicz, 2012; Dong et al., 2022). For example, the oil pipeline of Texaco Company in the United States was damaged by a submarine landslide, causing the leakage of 2100 gallons of crude oil into the sea (Zhao et al., 2021). In 2006, many submarine cables were damaged by a submarine landslide induced by the Pingtung earthquake in Taiwan, resulting in a major failure of international communication and substantial financial losses (Hsu et al., 2008). In 2009, two deepwater pipelines were destroyed by a submarine landslide triggered by the Suruga Bay earthquake in Japan (Matsumoto et al., 2010). In addition, submarine landslides may generate huge waves and lead to secondary disasters such as tsunamis. For example, the 1998 Papua New Guinea submarine landslide-induced tsunami resulted in over 2000 fatalities, destroyed numerous villages, and left more than 12000 people homeless (Tappin et al., 2001). In 2011, an earthquake-induced submarine landslide occurred in northeastern Japan and triggered a huge tsunami, killing tens of thousands of people and causing extensive damage to coastal buildings (Strasser et al., 2013). Moreover, in 2018, a submarine landslide-induced tsunami was triggered by a 7.5 magnitude earthquake in Sulawesi, Indonesia, which killed and injured more than 2000 people and caused extensive property damage (Pakoksung et al., 2019). Therefore, the safety of marine infrastructure can be ensured by obtaining a comprehensive understanding of the kinetic characteristics of submarine landslides and their impact on surrounding structures.
The extremely complicated submarine environment increases the difficulty of directly observing and monitoring the occurrence and movement processes of submarine landslides. Hence, physical model tests and numerical simulations are still the leading methods for studying the kinetic characteristics of submarine landslides. In terms of model tests, Watts (1998, 2000) established a series of flume model experiments to qualitatively and quantitatively investigate the wave characteristics generated by underwater landslides in solid blocks. Wiegel (1995) studied the influences of different initial submerged states, sliding angles, and water depths on the height and period of tsunami waves triggered by underwater landslides. Ataie-Ashtiani and Najafi-Jilani (2008) conducted 120 laboratory tests to analyze the effect of seabed slope angle, initial inundation, sliding geometry, shape, and deformation on shock wave properties, such as amplitude and period. Pilvar et al. (2019) studied the sliding forms of three different slopes, material types, and bed roughness and established a non-constant theoretical model to forecast the average velocity of underwater granular landslides. Zakeri et al. (2008) investigated the effect of clay-rich submarine mudflows on pipelines with two different placement forms (suspended and laid on the seafloor) by performing extensive flume model tests. They also proposed an equation to estimate the impact force of submarine landslides on the pipeline. Sahdi et al. (2014) explored the influence of soil strength, density, and the relative pipe-soil velocity on the impact force based on centrifuge model tests. They evaluated the impact forces of the submarine landslide by introducing a method that comprehensively considers geomechanics and hydrodynamics. Dai et al. (2017) discussed the relationship between the impact force and the sliding velocity, landslide volume, and cable diameter. Some achievements have been obtained through the above research. However, constraints such as scale effect, cost, and space limitation may be encountered by experimental studies.
Numerical simulation has recently been rapidly developed as an important alternative approach to investigating the motion and impact behavior of submarine landslides. For example, Yavari-Ramshe and Ataie-Ashtiani (2017) used the finite volume method (FVM) with nonlinear wet/dry transition treatment to investigate the submarine landslidetriggered wave. Zakeri et al. (2009) simulated the impact of submarine landslides on the suspended and laid-on-seafloor pipelines by applying the FVM method combined with the Herschel-Bulkley rheological model and validated the numerical results by comparing them with the experimental data. Considering three-phase media, Zhao et al. (2021) developed a coupled immersed boundary model to investigate the hydrodynamic load and vibration of pipelines exerted by submarine landslides. Fu and Jin (2015) employed the moving particle semi-implicit method to simulate the submarine landslide surge phenomenon and improved the model through a smoothing term and a pressure oscillation reduction method. Zhang et al. (2019) simulated the submarine landslide impact on pipelines at various impact angles using the computational fluid dynamics (CFD) model. Guo et al. (2022) introduced a CFD-based approach to quantitatively analyze the composition of drag forces on suspended pipelines exerted by submarine landslides. Dong et al. (2017) simulated the effect of the transient process of submarine landslides on the pipeline embedded in the seabed using the material point method combined with the Herschel-Bulkley rheological model. The smooth particle hydrodynamics (SPH) method has recently been widely used in multiphase or multiphysics problems due to its unique advantages in handling large deformations, free surfaces, and moving interfaces. For example, Ritchie and Thomas (2001) adapted the SPH technique to enable a multiphase fluid, which facilitates the free intermixing of SPH particles with widely different densities. Zhu et al. (2018) presented an SPH model for simulating multiphase fluid flows with large density ratios, which demonstrated the effective capture of inherent multiphase flow physics. Shimizu et al. (2020) introduced an enhanced multiphase ISPH-based method to simulate oil spill problems. Small-scale turbulence and the oil-water mixing effects were reproduced and captured in the simulations. Khayyer et al. (2023) improved the resolution of the continuity equation in the explicit weakly compressible SPH (WCSPH) model for the simulation of incompressible free-surface fluid flows. Enhanced satisfaction with incompressibility conditions and invariant density conditions were achieved. In addition, Luo et al. (2021) provided a state-of-the-art review of the applications of the SPH method in multiphase and multiphysics problems and emphasized the future perspectives of extending this method to a wide range of ocean and coastal engineering applications. The SPH method has been extensively applied in the simulation of submarine landslides in the past decade. For instance, Capone et al. (2010) applied the SPH method and established the underwater landslide as a non-Newtonian Bingham fluid to simulate the process of submarine landslide motion as well as wave generation. Qi et al. (2022) introduced a new multiphase SPH method for simulating various types of submarine landslides in surge experiments. Yeylaghi et al. (2017) simulated subaerial and submarine landslides through the development of an incompressible SPH (ISPH) model. Zhang et al. (2022) simulated the production and propagation of tsunami waves from submarine and subaerial landslides by developing a WCSPH model based on two-phase mixing theory and a large eddy simulation (LES) turbulence model. SPH has recently been coupled with other numerical algorithms for submarine landslide simulation. For instance, Qiu et al. (2017) simulated tsunamis generated by submerged, rigid, and deformed landslides using a combination of the discrete element method (DEM) and SPH. They employed a combination of the Papanastasiou and Herschel-Bulkley rheological models to capture the viscoplastic behavior of non-Newtonian flows in submarine-deformed landslides. Peng et al. (2020) developed an SPH model coupled with (discontinuous deformational analysis) DDA to address the fluid-solid interaction involved in submarine landslide propagation. The above studies reveal the unique advantages of the SPH method in simulating submarine landslide movement due to its meshfree and self-adaptability characteristics. Mean-while, SPH simulations of the impact behavior of fluids on structures have also produced some research results (Marrone et al., 2011; Pan et al., 2016; Li et al., 2020). However, investigations into the impact behavior of submarine landslides are still limited.
An SPH-based multiphase flow model is established in this paper to simulate the motion and impact behavior of submarine landslides. This model considers the landslide body and the ambient water as non-Newtonian and Newtonian fluids, respectively. The influence of particle resolution and rheological parameters on the motion behavior of submarine landslides is investigated, and the accuracy of the model in predicting the submarine landslide impact force on cable is validated.
2 Multiphase Flow SPH Model 2.1 SPH FormulationThe SPH method was originally applied to the simulation of astrophysical problems (Gingold and Monaghan, 1977; Lucy, 1997). Owing to its continuous improvement (Tafuni et al., 2018; Khayyer et al., 2023), the SPH method is increasingly used in the simulation of problems in the multiphase flow field, such as submarine landslides, wave impacts, and oil spills (Shimizu et al., 2020; Luo et al., 2021; Mahallem et al., 2022; Su et al., 2022). In the SPH method, the continuous fluid (or solid) is replaced by finitely interacting particles. Each particle contains field variables such as mass, pressure, and velocity, and the approximate values of the field variables are calculated using the weighted average of the interactions with other particles in the support domain (Gomez-Gesteira et al., 2010; Snelling et al., 2020). The SPH discretization of the governing equation is performed in two separate steps: 1) kernel approximation, which applies an integral representation to an arbitrary function, and 2) particle approximation, which transforms the integral form into a discretized one. Therefore, the approximate field variable functions f (xi) and their derivatives ∇f (xi) in the SPH method are shown as follows (Liu and Liu, 2010):
| $ f\left({{{\boldsymbol{x}}_i}} \right) \approx \sum\limits_{j = 1}^N {\frac{{{m_j}}}{{{\rho _j}}}} f\left({{{\boldsymbol{x}}_j}} \right){W_{ij}}, $ | (1) |
| $ \nabla f\left({{{\boldsymbol{x}}_i}} \right) \approx \sum\limits_{j = 1}^N {\frac{{{m_j}}}{{{\rho _j}}}} f\left({{{\boldsymbol{x}}_i}} \right){\nabla _i}{W_{ij}}, $ | (2) |
| $ {\nabla _i}{W_{ij}} = \frac{{{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}}}{{\left| {{{\boldsymbol{r}}_{ij}}} \right|}}\frac{{\partial W\left({\left| {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right|, h} \right)}}{{\partial {{\boldsymbol{r}}_{ij}}}}, $ | (3) |
where x is the coordinate of the SPH particle, m is the mass of the particle, ρ is the density, h is the smooth length, rij = xi – xj is the distance between particles, N is the total number of neighboring particles in the support domain, and W is the smooth kernel function. The quintic spline kernel function proposed by Morris (1996) is applied in this study, as shown in Eq. (4):
| $ W(q, h)=\alpha_d \times\left\{\begin{array}{l} (3-q)^5-6(2-q)^5+15(1-q)^5, 0 \leq q <1 \\ (3-q)^5-6(2-q)^5, 1 \leq q <2 \\ (3-q)^5, 2 \leq q <3 \\ 0, q \geq 3 \end{array}\right., $ | (4) |
where q = |rij|/h, αd = 7/(478πh2).
2.2 Governing EquationsThe underwater landslide is treated as a weakly compressible viscous flow, which satisfies the law of mass and momentum conservation, and the corresponding governing equations are shown below:
| $ \frac{\mathrm{d} \rho}{\mathrm{~d} t}=-\rho \nabla \cdot \boldsymbol{v}, $ | (5) |
| $ \frac{\mathrm{d} v}{\mathrm{~d} t}=-\frac{1}{\rho} \nabla p+\frac{1}{\rho} \boldsymbol{F}_{\mathrm{vis}}+g, $ | (6) |
where t is the time, v is the velocity vector, g is the gravitational acceleration, Fvis is the viscous force of the fluid, and p is the pressure term of the fluid, which is calculated using the following equation of state (Monaghan, 2012):
| $ p = {\rho _0}c_s^2\left[ {\left({\frac{\rho }{{{\rho _0}}} - 1} \right)} \right] + \chi, $ | (7) |
where ρ0 is the reference density, cs is the sound velocity, and χ is the background pressure. cs should be greater than 10 times the maximum velocity to ensure that the density fluctuations are within 1% and substantially less than the true velocity, thereby avoiding extremely small time steps. cs is typically limited by the following equation (Meringolo et al., 2018):
| $ {c_s} \geqslant 10\max \left({\sqrt {\frac{{{p_{\max}}}}{{{\rho _0}}}}, {v_{\max}}} \right), $ | (8) |
where pmax and vmax are the estimated maximum pressure and velocity in the flow field, respectively. As shown below, the two phases are required to satisfy the ρ0cs2 conservation (Colagrossi and Landrini, 2003) and enhance the stability and accuracy of the simulations:
| $ {\rho _{{0_1}}}c_{{s_1}}^2 = {\rho _{{0_2}}}c_{{s_2}}^2, $ | (9) |
where subscripts 1 and 2 indicate the landslide particle and water phases, respectively.
During calculation in the pressure field, numerical oscillations in the traditional WCSPH method may be attributed to the density approximation. Therefore, in this study, an artificial diffusion term Di is added to the continuity equation to effectively eliminate the high-frequency numerical noise.
| $ {D_i} = 2\delta {h_i}{c_s}\sum\limits_{j = 1}^N {{\boldsymbol{\psi}_{ij}}} {V_j}{\nabla _i}{W_{ij}}, $ | (10) |
where V denotes the volume of the particle, and δ is the dimensionless coefficient, which is usually taken as δ = 0.1. The term ψij uses the modified form proposed by Molteni and Colagrossi (2009) and Krimi et al. (2018):
| $ {\boldsymbol{\psi}_{ij}} = \left({{\beta _{{\rho _i}}} - {\beta _{{\rho _j}}}} \right){\rho _{0i}}\frac{{{\boldsymbol{r}_{ij}}}}{{{{\left| {{\boldsymbol{r}_{ij}}} \right|}^2}}}, $ | (11) |
where βρ is the density ratio of a particle in terms of its initial reference density, i.e., βρ = ρ/ρ0.
2.3 Viscous ItemThe acceleration due to viscous forces is shown as follows (Adami et al., 2010):
| $ \frac{1}{\rho} \boldsymbol{F}_{\mathrm{vis}}=\frac{1}{m_i} \sum\limits_{j=1}^N \frac{2 \mu_i \mu_j}{\mu_i+\mu_j}\left(V_i^2+V_j^2\right) \times \frac{\boldsymbol{r}_{i j} \cdot \nabla_i W_{i j}}{\left|\boldsymbol{r}_{i j}\right|^2} \boldsymbol{v}_{i j}, $ | (12) |
where μ is the dynamic viscosity of the particle. The viscosity for water particles is calculated based on the Newtonian fluid model, while μ for landslide particles is derived using the non-Newtonian Herschel-Bulkley rheological model. The expression is as follows:
| $ \mu = \eta {\left| {\dot \gamma } \right|^{K - 1}} + \frac{{{\tau _y}}}{{\left| {\dot \gamma } \right|}}, $ | (13) |
where τy is the yield stress, η is the viscosity coefficient, K is the power-law exponent, and their magnitude is determined by the specific material.
| $ \dot{\gamma}=\nabla \boldsymbol{v}+(\nabla \boldsymbol{v})^{\mathrm{T}},, $ | (14) |
where ∇ν and (∇ν)T represent the velocity gradient and transpose tensors, respectively.
2.4 Boundary ConditionsIn the simulation of the submarine landslides, the support domain of fluid particles near the solid wall is truncated by the wall boundary, leading to a reduction in computational accuracy. Adami et al. (2012) proposed a solidwall virtual particle boundary condition that discretizes the solid-wall boundary into a series of virtual particles with physical quantities, as shown in Fig.1. This method not only prevents the penetration of the fluid particles near the boundary but also maintains the continuity of the pressure, density, and other physical fields of the fluid particles near the boundary to improve the computational accuracy of the simulation. Therefore, this paper applied the aforementioned boundary condition in the simulation of the multiphase flow problem of submarine landslides. The physical quantity of ghost particles is obtained by interpolating the neighboring fluid particles, and the pressure can be expressed by Eq. (14):
| $ {p_b} = \frac{{\sum\limits_f {{p_f}{W_{bf}} + \left({g - {{a}_w}} \right)\sum\limits_f {{p_f}\left({{{x}_b} - {{x}_f}} \right){W_{bf}}} } }}{{\sum\limits_f {{W_{bf}}} }}, $ | (15) |
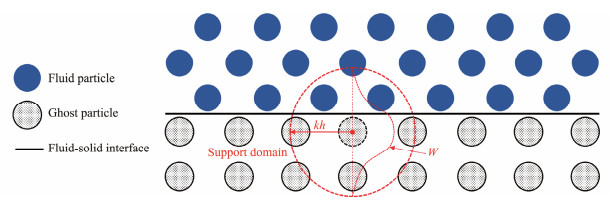
|
Fig. 1 Schematic illustration of the solid boundary treatment. |
where the subscript b denotes solid-wall ghost particles, the subscript f denotes fluid particles, and aw is the acceleration at the wall boundary.
A free slip boundary condition is implemented by the model by ignoring the viscous force interaction between fluid particles and neighboring ghost particles. Ghost particles for the no-slip boundary condition are imposed via interpolation with the interacting fluid particles to obtain the velocity. The expression for the ghost particle velocity is given as follows:
| $ \boldsymbol{v}_b=2 \boldsymbol{v}_w-\frac{\sum\limits_f \boldsymbol{v}_f W_{b f}}{\sum\limits_f W_{b f}}, $ | (16) |
where vw is the velocity of the solid wall.
Solid boundary particles are used to build the structure to simulate the impact force of submarine landslides on the structure, and the virtual acceleration of the structure can be obtained by solving Eq. (5). The total impact force can then be calculated by multiplying the acceleration with the particle mass (Crespo et al., 2015; Klapp et al., 2020). The specific expression is shown below:
| $\frac{\mathrm{d} \boldsymbol{v}_s}{\mathrm{~d} t}=-\frac{1}{m_s} \sum\limits_f\left(p_s V_s^2+p_f V_f^2\right) \nabla_s W_{s f}+\frac{1}{m_s} \sum\limits_f \frac{2 \mu_s \mu_f}{\mu_s+\mu_f}\left(V_s^2+V_f^2\right) \times \frac{\boldsymbol{r}_{s f} \cdot \nabla_s W_{s f}}{\left|\boldsymbol{r}_{s f}\right|^2} \boldsymbol{v}_{s f}, $ | (17) |
| $ \boldsymbol{F}=m \sum\limits_s \frac{\mathrm{~d} \boldsymbol{v}_s}{\mathrm{~d} t}, $ | (18) |
where the subscript s denotes the structure particle, the subscript f denotes the fluid particle, and F denotes the impact force on the structure.
2.5 Time-Step SchemeRestricting the size of the time step by imposing an artificial term that is related to the sound velocity, viscous diffusion term, and fluid maximum acceleration conditions is necessary to ensure the stability of the simulation (Monaghan, 1992, 2005; Morris et al., 1997). The time-step constraints are shown below:
| $ \Delta t \leq \min \left(1.25 \frac{h}{c_s}, 0.125 \frac{h^2}{\max \left(\frac{\mu_i}{\rho_i}\right)}, 0.25 \mathrm{~min} \sqrt{\frac{h}{\left|\boldsymbol{a}_i\right|}}\right), $ | (19) |
where a is the acceleration of the particle.
3 Model Validation and Application 3.1 Two-Phase Hydrostatic TankThe stability and accuracy of multiphase flow models are validated by widely simulating the two-phase hydrostatic tank as a benchmark problem (Krimi et al., 2018; Rezavand et al., 2020). As shown in Fig.2, a two-dimensional rectangular tank with a width of 0.4 m is filled with two stratified fluids. The upper and lower layers are light and heavy fluids with densities of 1000 and 2000 kg m−3, respectively. Both fluids are subjected to a vertical gravitational acceleration of 9.81 m s−2. The upper fluid behaves as a Newtonian fluid with a constant viscosity of η1 = 0.02 Pa s, while the lower fluid behaves as a Herschel-Bulkley rheological fluid with a viscosity coefficient η2 = 0.001 Pa s, a power-law exponent N = 2, and a yield strength τy = 250 Pa.
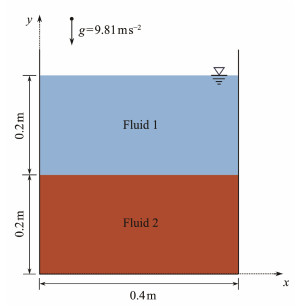
|
Fig. 2 Geometric configuration of the two-phase hydrostatic tank case. |
The two-phase hydrostatic tank model is replaced by SPH particles with three different sizes (dp = 0.001, 0.002, and 0.004 m) to investigate the influence of SPH particle size on the simulation accuracy. Fig.3 shows the simulated pressure field of the model with three particle sizes. The pressure distributions are smooth, and pressure discontinuity and oscillation are absent. The model with fine particle resolutions can obtain highly stable results.
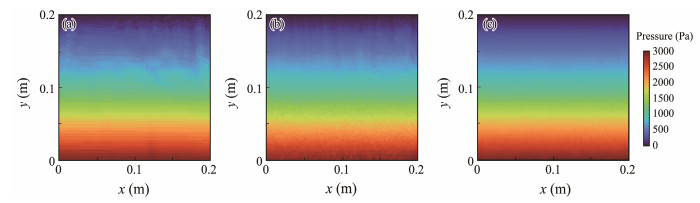
|
Fig. 3 SPH simulated pressure field of the hydrostatic tank with different particle sizes. (a), dp = 0.004 m; (b), dp = 0.002 m; (c), dp = 0.001 m. |
The numerical results are compared with the analytical solution to validate the simulation accuracy of the multiphase flow SPH model. As shown in Fig.4, the vertical pressure distribution obtained using SPH simulation is close to the analytical solution.
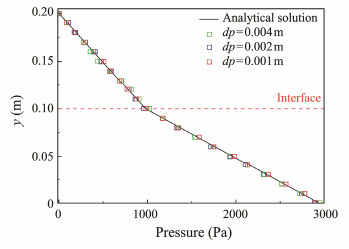
|
Fig. 4 Comparison of the pressure distribution along the y-direction. |
The L2 error in pressure is calculated using the following equation to quantify the error between the numerical and analytical results:
| $ {L_2}{\kern 1pt} {\rm error} = \frac{{\left\| {p - \hat p} \right\|}}{{\left\| {\hat p} \right\|}}, $ | (20) |
where p is the calculated pressure in the SPH simulation, and
| $ \|p\|=\left(\int\limits_{\Omega_0} p \cdot p \mathrm{~d} \Omega_0\right)^{1 / 2}. $ | (21) |
Fig.5 shows the convergence curves of the multiphase flow SPH model. These curves indicate the small L2 error of the model, which decreases as the number of particles increases.

|
Fig. 5 Convergence curve with different discretization. |
The numerical experiment in this section shows consistency between the simulated pressures of the multiphase flow SPH model and those of the analytical solution, and the SPH model with fine particle resolution can obtain highly accurate results.
3.2 Waves Generated by the Submarine LandslideA physical model test designed by Rzadkiewicz et al. (1997) is simulated as a case study in this paper to validate the computational accuracy of the multiphase flow SPH model. The test was conducted in a 4 m × 2 m water tank with a maximum water depth of 1.6 m. The slide body with a cross-sectional area of 0.65 m × 0.65 m was placed on the slope with an inclined angle of 45˚. Fig.6 shows the schematic of the model test. The densities of the landslide body and ambient water were 1950 and 1000 kg m−3, respectively. The Herschel-Bulkley rheological model is introduced to describe the landslide behavior, and the Newtonian fluid model is used for the simulation of the surrounding water.
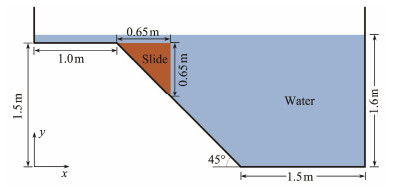
|
Fig. 6 Geometric configuration of underwater deformation landslide experiment. |
The rheological parameters used in this paper are selected in accordance with the simulations performed by Ataie-Ashtiani and Shobeyri (2008), τy = 750 Pa and η = 0.15 Pa s. Fig.7 shows the pressure field of the water at different moments. The figure shows the absence of pressure oscillation and a relatively continuous and smooth pressure field. Fig.8 shows the velocity vector of the fluid phase, which describes the interaction between a landslide and water. When the landslide body slides downward under the effect of gravity, its kinetic energy is transferred to the ambient water, thus inducing surge waves at the water surface and creating a vortex above the front of the slide.

|
Fig. 7 SPH simulated results of the pressure field at typical times. (a), t = 0.4 s; (b), t = 0.6 s; (c), t = 1.2 s. |
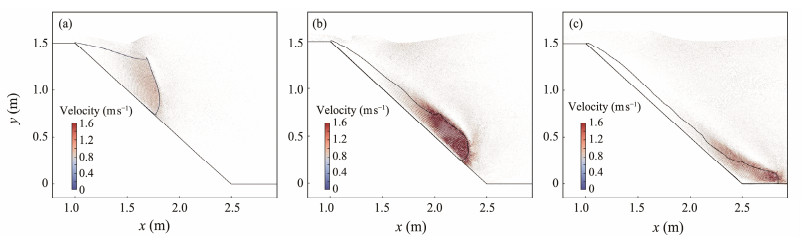
|
Fig. 8 SPH simulated results of the velocity vector at typical times. (a), t = 0.4 s; (b), t = 0.6 s; (c), t = 1.2 s. |
The landslide profiles at the moments of 0.4 and 0.8 s are compared with the experimental results recorded in Rzadkiewicz et al. (1997) and the ISPH results presented in Ataie-Ashtiani and Shobeyri (2008) to validate the accuracy of the multiphase flow SPH model. Fig.9 shows some discrepancies between measured and simulated landslide profiles. When t = 0.8 s, the sliding velocity of the landslide body is relatively high, resulting in a strong interaction between soil particles and the ambient water. Therefore, water erodes the soil particles in the landslide front, leading to a thick landslide front. However, the SPH particles in the numerical model are substantially larger than the real soil particles and are thus difficult to erode by the water. Therefore, the simulated landslide profile near the front cannot accurately match the experimental results.
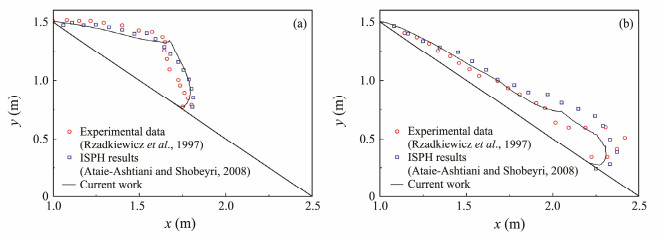
|
Fig. 9 Comparison of the underwater landslide profiles at typical times. (a), t = 0.4 s; (b), t = 0.8 s. |
The simulated surface wave profiles are compared with the experimental observations in Rzadkiewicz et al. (1997) and the numerical results in Capone et al. (2010) and Bu et al. (2022) (as shown in Fig.10) to further validate the simulation accuracy of the SPH model. The goodness of fit R2 is applied for the quantitative analysis of the results, and the calculated expression is shown in Eq. (21). In this case, the y-direction coordinates (y1, y2, y3, ···, y35) of 35 points with equal horizontal distances on the wave profile are selected for the analysis.
| $ {R^2} = 1 - \frac{{\sum\limits_{i = 1}^n {{{\left({{y_i} - {{\hat y}_i}} \right)}^2}} }}{{\sum\limits_{i = 1}^n {{{\left({{y_i} - {{\bar y}_i}} \right)}^2}} }} . $ | (22) |
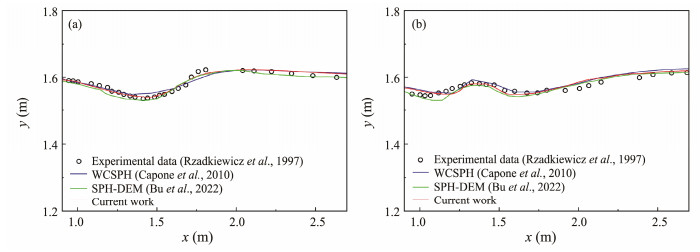
|
Fig. 10 Comparison of the experimental and simulated wave profiles at typical times. (a), t = 0.4 s; (b), t = 0.8 s. |
Table 1 shows the calculated goodness of fit. The calculated fitness is greater than 0.8, which indicates that the numerical results agree well with those from the experimental and existing numerical models. Therefore, the landslide-induced wave phenomenon can be effectively reproduced by the SPH model established in this paper.
|
|
Table 1 Goodness of fit between the numerical and experimental results on the wave profiles |
Sensitivity analysis of η and τy of the Herschel-Bulkley rheological model is conducted based on the above results to analyze the influence of rheological parameters of landslides on the characteristics of landslide motion. The maximum frontal velocity vf-max of the granular landslide and the landslide body profile at 0.8 s are simulated, and the results are shown in Fig.11. The vf-max of the submarine landslide gradually increases with the decrease in η and τy, and τy has a notable influence on the vf-max, as shown in Figs. 11a and 11b. Fig.11c shows that the landslide configuration at 0.8 s slightly changes with the variation of η when the η value is small. The landslide movement distance considerably shortens only when the η value is large. Fig.11d shows the acceleration of landslide flows and the extension of the sliding distance at 0.8 s with the reduction in τy. Therefore, the rheological parameter τy has a more notable influence on the mobility of the landslide body compared with the viscosity coefficient η.

|
Fig. 11 Sensitivity analysis of rheological parameters. (a), vf-max against different η; (b), vf-max against different τy; (c), landslide profiles for different η at 0.8 s; (d), landslide profiles for different τy at 0.8 s. |
A rotating flume experiment conducted by Wang et al. (2018) to replicate the impact of an underwater landslide on a cable is simulated to validate the SPH impact model established in this work. Fig.12 shows the schematic of the model test. The main part of the apparatus is an annular trough with an axle in the center. The outer radius, inner radius, and width of the trough are 0.9, 0.6, and 0.4 m, respectively. The axle of the apparatus is connected to a motor to facilitate rotation in a vertical plane at a controlled velocity. A certain amount of water and soil material is placed in the apparatus to simulate the submarine landslide. The fine silica sand used in the experiment as the landslide body is assumed to be a Herschel-Bulkley fluid in the simulation. A cable is installed in the bottom of the annular trough parallel to the axel. The cable comprises stainless steel with a length of 370 mm. The height of the cable from the frame bottom is 0.2 m.
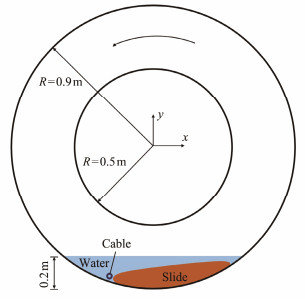
|
Fig. 12 Geometric configuration of the submarine landslide impact on a cable experiment. |
Two load cells are set at two sides of the cable to measure the impact force from the water and landslide mass. The measurement range of the load cell is 20 N, and the measuring precision is 0.1 N. A water pressure transducer with a measurement range of 10 kPa and a precision of 0.1 kPa is fixed inside the frame bed to measure the water pressure during the experiment.
The water and the landslide body remain at the bottom during the rotation due to the effect of gravity. The cable moves at a certain speed and impacts the water and the landslide, simulating the process of a submarine landslide impacting the cable. Fig.13 shows the SPH-simulated velocity fields at different times with the flume rotation at 0.38 m s−1. The dry weight of the landslide body is 30 kg, and the cable diameter is 20 mm. The cable has a certain effect on the velocity field of the surrounding fluid, and a vortex appears near the cable as it moves. The initial state of the soilwater mixture is disturbed when the cable starts to move, and the surrounding water agitates the sand particles. Turbid fluid appears along the cable trace. Fig.14 shows that the initial smooth pressure field of the soil-water mixture is also disturbed due to the impact of the cable.
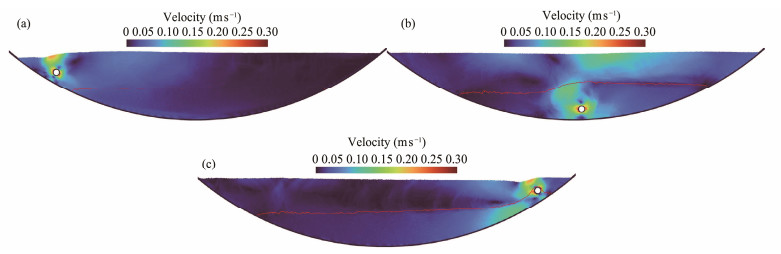
|
Fig. 13 SPH simulated results for the velocity field at different time. (a), t = 5.0 s; (b), t = 7.0 s; (c), t = 9.0 s. |

|
Fig. 14 SPH simulated results for the pressure field at typical time. (a), t = 5.0 s; (b), t = 7.0 s; (c), t = 9.0 s. |
The impact force and water pressure are compared with the experimental data to validate the simulation accuracy of the SPH model. As shown in Fig.15, the evolution of the simulated impact force and water pressure curves agrees well with the experimental data, and the peak values of the calculated impact force and water pressure are close to the measured data. The goodness of fit R2 is calculated and listed in Table 2. The R2 of impact force and water pressure are both greater than 0.8, indicating that the SPH simulation results fit well with the measured data in the experiments. Convergence analysis of impact force and pressure time history curves is conducted, and the L2 error formula (Eqs. (20) and (21)) is used to calculate the error of different particle spacing (dp = 0.001, 0.002, and 0.004 m), as shown in Fig.16. The simulated results of impact force and pressure are closer to the test data as the number of particles increases.
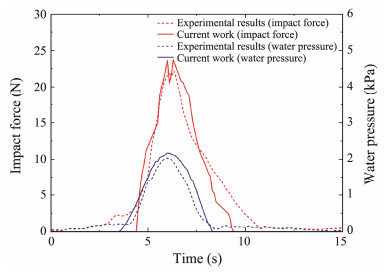
|
Fig. 15 Contrast curve of impact force and water pressure. |
|
|
Table 2 Goodness of fit between the numerical and experimental results on impact force and water pressure |
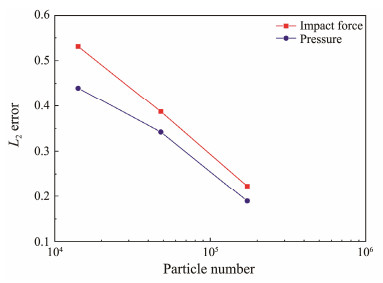
|
Fig. 16 Convergence curves for impact force and pressure. |
Fig.17 shows a comparison between the measured peak impact force F and the results obtained from the SPH simulation under different silica sand mass m. The diameter of the pipe is 20 mm, and the velocity of the landslide body is 0.38 m s−1. The simulated peak impact forces are closer to the experimental data. Therefore, the submarine landslide-cable interaction can be reproduced by the SPH model with certain accuracy.
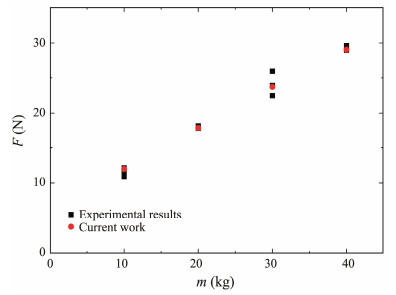
|
Fig. 17 Impact force under different sand mass. |
Submarine landslides seriously threaten coastal marine infrastructure as well as human life due to their immense impact force and the generation of huge waves. An SPH-based multiphase flow model is presented in this paper to simulate submarine landslide motion and impact behavior. The Herschel-Bulkley and Newton fluid models are introduced to simulate the submarine landslide body and the ambient water, respectively. The model is improved by applying artificial diffusion terms and multiphase flow corrections to the equation of state to ensure numerical accuracy and stability.
The accuracy and stability of the multiphase flow SPH model are validated by simulating and analyzing three benchmark cases. The computational accuracy of the SPH model increases with particle resolution. Sensitivity analysis shows that the rheological parameter τy has a more notable influence on the mobility of the landslide body compared with the viscosity coefficient η. The numerical results are compared with the analytical solution, experimental data, and simulated results obtained from other numerical models. Therefore, the SPH model is suitable for predicting the impact force of submarine landslides exerted on cables.
The multiphase model presented in this paper demonstrates good performance in simulating the motion and impact behavior of submarine landslides in two dimensions. However, the real submarine landslide occurs in a three-dimensional space with complex submarine topography. Therefore, a 3D model with high-efficiency parallel computing technology is necessary to reproduce the real motion and impact behavior of submarine landslides.
AcknowledgementsThis work was supported by the National Natural Science Foundation of China (Nos. 42472332, 42102318 and 42006143), the Open Research Fund Program of Zhoushan Field Scientific Observation and Research Station for Marine Geo-Hazards, China Geological Survey (No. ZSORS-22-07), the Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning (No. TP2019037), and the Open Research Fund Program of Marine Ecological Restoration and Smart Ocean Engineering Research Center of Hebei Province (No. HB MESO2312).
Author Contributions
All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Baisen Lan. The draft of the manuscript was written by Zili Dai, and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Data Availability
All data generated and analyzed during this study are included in this published article and its additional files.
Declarations
Ethics Approval and Consent to Participate
This article does not contain any studies with human participants or animals performed by any of the authors.
Consent for Publication
Informed consent for publication was obtained from all participants.
Conflict of Interests
The authors declare that they have no conflict of interests.
Adami, S., Hu, X. Y., and Adams, N. A., 2010. A new surfacetension formulation for multi-phase SPH using a reproducing divergence approximation. Journal of Computational Physics, 229(13): 5011-5021. DOI:10.1016/j.jcp.2010.03.022 (  0) 0) |
Adami, S., Hu, X. Y., and Adams, N. A., 2012. A generalized wall boundary condition for smoothed particle hydrodynamics. Journal of Computational Physics, 231(21): 7057-7075. DOI:10.1016/j.jcp.2012.05.005 (  0) 0) |
Ataie-Ashtiani, B., and Najafi-Jilani, A., 2008. Laboratory investigations on impulsive waves caused by underwater landslide. Coastal Engineering, 55(12): 989-1004. DOI:10.1016/j.coastaleng.2008.03.003 (  0) 0) |
Ataie-Ashtiani, B., and Shobeyri, G., 2008. Numerical simulation of landslide impulsive waves by incompressible smoothed particle hydrodynamics. International Journal for Numerical Methods in Fluids, 56(2): 209-232. DOI:10.1002/fld.1526 (  0) 0) |
Bu, S., Li, D., Chen, S., Xiao, C., and Li, Y., 2022. Numerical simulation of landslide-generated waves using a SPH-DEM coupling model. Ocean Engineering, 258: 111826. DOI:10.1016/j.oceaneng.2022.111826 (  0) 0) |
Capone, T., Panizzo, A., and Monaghan, J. J., 2010. SPH modelling of water waves generated by submarine landslides. Journal of Hydraulic Research, 48: 80-84. DOI:10.1080/00221686.2010.9641248 (  0) 0) |
Colagrossi, A., and Landrini, M., 2003. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. Journal of Computational Physics, 191(2): 448-475. DOI:10.1016/S0021-9991(03)00324-3 (  0) 0) |
Crespo, A. J., Domínguez, J. M., Rogers, B. D., Gómez-Gesteira, M., Longshaw, S., Canelas, R. J. F. B., et al., 2015. DualSPH-ysics: Open-source parallel CFD solver based on Smoothed Particle Hydrodynamics (SPH). Computer Physics Communications, 187: 204-216. DOI:10.1016/j.cpc.2014.10.004 (  0) 0) |
Dai, Z., Wang, F., and Nakahara, Y., 2017. Experimental study on impact behavior of submarine landslides on communication cables. In: Advancing Culture of Living with Landslides. WLF2017. Springer, Cham, 617-622, DOI: 10.1007/978-3-319-53485-5_71.
(  0) 0) |
Dong, Y., Cui, L., and Zhang, X., 2022. Multiple‐GPU parallelization of three‐dimensional material point method based on single-root complex. International Journal for Numerical Methods in Engineering, 123(6): 1481-1504. DOI:10.1002/nme.6906 (  0) 0) |
Dong, Y., Wang, D., and Randolph, M. F., 2017. Investigation of impact forces on pipeline by submarine landslide using material point method. Ocean Engineering, 146: 21-28. DOI:10.1016/j.oceaneng.2017.09.008 (  0) 0) |
Fu, L., and Jin, Y. C., 2015. Investigation of non-deformable and deformable landslides using meshfree method. Ocean Engineering, 109: 192-206. DOI:10.1016/j.oceaneng.2015.08.051 (  0) 0) |
Gingold, R. A., and Monaghan, J. J., 1977. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Monthly Notices of the Royal Astronomical Society, 181(3): 375-389. DOI:10.1093/mnras/181.3.375 (  0) 0) |
Gómez-Gesteira, M., Rogers, B. D., Dalrymple, R. A., and Crespo, A. J., 2010. State-of-the-art of classical SPH for free-surface flows. Journal of Hydraulic Research, 48: 6-27. DOI:10.1080/00221686.2010.9641242 (  0) 0) |
Guo, X. S., Zheng, D. F., Zhao, L., Fu, C. W., and Nian, T. K., 2022. Quantitative composition of drag forces on suspended pipelines from submarine landslides. Journal of Waterway, Port, Coastal, and Ocean Engineering, 148(1): 04021050. DOI:10.1061/(ASCE)WW.1943-5460.0000680 (  0) 0) |
Hsu, S. K., Kuo, J., Lo, C. L., Tsai, C. H., Doo, W. B., Ku, C. Y., et al., 2008. Turbidity currents, submarine landslides and the 2006 Pingtung earthquake off SW Taiwan. Terrestrial, Atmospheric and Oceanic Sciences, 19(6): 767-772. DOI:10.3319/TAO.2008.19.6.767(PT) (  0) 0) |
Khayyer, A., Shimizu, Y., Gotoh, T., and Gotoh, H., 2023. Enhanced resolution of the continuity equation in explicit weakly compressible SPH simulations of incompressible free-surface fluid flows. Applied Mathematical Modelling, 11: 84-121. DOI:10.1016/j.apm.2022.10.037 (  0) 0) |
Klapp, J., Areu-Rangel, O. S., Cruchaga, M., Aránguiz, R., Bonasia, R., Godoy, M. J., et al., 2020. Tsunami hydrodynamic force on a building using a SPH real-scale numerical simulation. Natural Hazards, 100: 89-109. DOI:10.1007/s11069-019-03800-3 (  0) 0) |
Krimi, A., Khelladi, S., Nogueira, X., Deligant, M., Ata, R., and Rezoug, M., 2018. Multiphase smoothed particle hydrodynamics approach for modeling soil-water interactions. Advances in Water Resources, 121: 189-205. DOI:10.1016/j.advwatres.2018.08.004 (  0) 0) |
Li, S., Peng, C., Wu, W., Wang, S., Chen, X., Chen, J., et al., 2020. Role of baffle shape on debris flow impact in step-pool channel: An SPH study. Landslides, 17: 2099-2111. DOI:10.1007/s10346-020-01410-w (  0) 0) |
Liu, M. B., and Liu, G., 2010. Smoothed particle hydrodynamics (SPH): An overview and recent developments. Archives of Computational Methods in Engineering, 17: 25-76. DOI:10.1007/s11831-010-9040-7 (  0) 0) |
Lucy, L. B., 1977. A numerical approach to the testing of the fission hypothesis. Astronomical Journal, 82: 1013-1024. DOI:10.1086/112164 (  0) 0) |
Luo, M., Khayyer, A., and Lin, P., 2021. Particle methods in ocean and coastal engineering. Applied Ocean Research, 114: 102734. DOI:10.1016/j.apor.2021.102734 (  0) 0) |
Mahallem, A., Roudane, M., Krimi, A., and Gouri, S. A., 2022. Smoothed particle hydrodynamics for modelling landslide-water interaction problems. Landslides, 19(5): 1249-1263. DOI:10.1007/s10346-021-01807-1 (  0) 0) |
Marrone, S., Antuono, M. A. G. D., Colagrossi, A., Colicchio, G., Le Touzé, D., and Graziani, G., 2011. δ-SPH model for simulating violent impact flows. Computer Methods in Applied Mechanics and Engineering, 200(13-16): 1526-1542. DOI:10.1016/j.cma.2010.12.016 (  0) 0) |
Matsumoto, H., Baba, T., Kashiwase, K., Kaneda, Y., Misu, T., and Hori, T., 2010. Damage of deep ocean water pipes due to the Suruga Bay earthquake on 11 August, 2009. Journal of Japan Society of Civil Engineers, Series B2 (Coastal Engineering), 66(1): 1341-1345. DOI:10.2208/kaigan.66.1341 (  0) 0) |
Meringolo, D. D., Liu, Y., Wang, X. Y., and Colagrossi, A., 2018. Energy balance during generation, propagation and absorption of gravity waves through the δ-LES-SPH model. Coastal Engineering, 140: 355-370. DOI:10.1016/j.coastaleng.2018.07.007 (  0) 0) |
Molteni, D., and Colagrossi, A., 2009. A simple procedure to improve the pressure evaluation in hydrodynamic context using the SPH. Computer Physics Communications, 180(6): 861-872. DOI:10.1016/j.cpc.2008.12.004 (  0) 0) |
Monaghan, J. J., 1992. Smoothed particle hydrodynamics. Annual Review of Astronomy and Astrophysics, 30(1): 543-574. DOI:10.1146/annurev.aa.30.090192.002551 (  0) 0) |
Monaghan, J. J., 2005. Smoothed particle hydrodynamics. Reports on Progress in Physics, 68(8): 1703-1759. DOI:10.1088/0034-4885/68/8/R01 (  0) 0) |
Monaghan, J. J., 2012. Smoothed particle hydrodynamics and its diverse applications. Annual Review of Fluid Mechanics, 44: 323-346. DOI:10.1146/annurev-fluid-120710-101220 (  0) 0) |
Morris, J. P., 1996. Analysis of smoothed particle hydrodynamics with applications. PhD thesis. Monash University.
(  0) 0) |
Morris, J. P., Fox, P. J., and Zhu, Y., 1997. Modeling low Reynolds number incompressible flows using SPH. Journal of Computational Physics, 136(1): 214-226. DOI:10.1006/jcph.1997.5776 (  0) 0) |
Pakoksung, K., Suppasri, A., Imamura, F., Athanasius, C., Omang, A., and Muhari, A., 2019. Simulation of the submarine landslide tsunami on 28 September 2018 in Palu Bay, Sulawesi Island, Indonesia, using a two-layer model. Pure and Applied Geophysics, 176: 3323-3350. DOI:10.1007/s00024-019-02235-y (  0) 0) |
Pan, K., IJzermans, R. H. A., Jones, B. D., Thyagarajan, A., Van Beest, B. W. H., and Williams, J. R., 2016. Application of the SPH method to solitary wave impact on an offshore platform. Computational Particle Mechanics, 3: 155-166. DOI:10.1007/s40571-015-0069-0 (  0) 0) |
Peng, X. Y., Yu, P. C., Chen, G. Q., Xia, M. Y., and Zhang, Y. B., 2020. Development of a coupled DDA-SPH method and its application to dynamic simulation of landslides involving solid-fluid interaction. Rock Mechanics and Rock Engineering, 53(1): 113-131. DOI:10.1007/s00603-019-01900-x (  0) 0) |
Perez-Gruszkiewicz, S. E., 2012. Reducing underwater-slide impact forces on pipelines by streamlining. Journal of Waterway, Port, Coastal, and Ocean Engineering, 138(2): 142-148. DOI:10.1061/(ASCE)WW.1943-5460.0000113 (  0) 0) |
Pilvar, M., Pouraghniaei, M. J., and Shakibaeinia, A., 2019. Twodimensional sub-aerial, submerged, and transitional granular slides. Physics of Fluids, 31(11): 113303. DOI:10.1063/1.5121881 (  0) 0) |
Qi, Y., Chen, J., Zhang, G., Xu, Q., and Li, J., 2022. An improved multi-phase weakly-compressible SPH model for modeling various landslides. Powder Technology, 397: 117120. (  0) 0) |
Qiu, L. C., Jin, F., Lin, P. Z., Liu, Y., and Han, Y., 2017. Numerical simulation of submarine landslide tsunamis using particle based methods. Journal of Hydrodynamics, 29(4): 542-551. DOI:10.1016/S1001-6058(16)60767-9 (  0) 0) |
Rezavand, M., Zhang, C., and Hu, X. Y., 2020. A weakly compressible SPH method for violent multi-phase flows with high density ratio. Journal of Computational Physics, 402: 109092. DOI:10.1016/j.jcp.2019.109092 (  0) 0) |
Ritchie, B. W., and Thomas, P. A., 2001. Multiphase smoothedparticle hydrodynamics. Monthly Notices of the Royal Astronomical Society, 323(3): 743-756. DOI:10.1046/j.1365-8711.2001.04268.x (  0) 0) |
Rzadkiewicz, S. A., Mariotti, C., and Heinrich, P., 1997. Numerical simulation of submarine landslides and their hydraulic effects. Journal of Waterway, Port, Coastal, and Ocean Engineering, 123(4): 149-157. DOI:10.1061/(ASCE)0733-950X(1997)123:4(149) (  0) 0) |
Sahdi, F., Gaudin, C., White, D. J., Boylan, N., and Randolph, M. F., 2014. Centrifuge modelling of active slide-pipeline loading in soft clay. Géotechnique, 64(1): 16-27. DOI:10.1680/geot.12.P.191 (  0) 0) |
Shimizu, Y., Khayyer, A., Gotoh, H., and Nagashima, K., 2020. An enhanced multiphase ISPH-based method for accurate modeling of oil spill. Coastal Engineering Journal, 62(4): 625-646. DOI:10.1080/21664250.2020.1815362 (  0) 0) |
Snelling, B. E., Collins, G. S., Piggott, M. D., and Neethling, S. J., 2020. Improvements to a smooth particle hydrodynamics simulator for investigating submarine landslide generated waves. International Journal for Numerical Methods in Fluids, 92(7): 744-764. DOI:10.1002/fld.4804 (  0) 0) |
Strasser, M., Kölling, M., Ferreira, C. D. S., Fink, H. G., Fujiwara, T., Henkel, S., et al., 2013. A slump in the trench: Tracking the impact of the 2011 Tohoku-Oki earthquake. Geology, 41(8): 935-938. DOI:10.1130/G34477.1 (  0) 0) |
Su, X., Luo, M., Zhao, X., and Khayyer, A., 2022. Oil spill spreading simulation based on an enhanced multi-phase consistent particle method. International Journal of Offshore and Polar Engineering, 32(4): 377-385. DOI:10.17736/ijope.2022.jc873 (  0) 0) |
Tafuni, A., Domínguez, J. M., Vacondio, R., and Crespo, A. J. C., 2018. A versatile algorithm for the treatment of open boundary conditions in Smoothed particle hydrodynamics GPU models. Computer Methods in Applied Mechanics and Engineering, 342: 604-624. DOI:10.1016/j.cma.2018.08.004 (  0) 0) |
Tappin, D. R., Watts, P., McMurtry, G. M., Lafoy, Y., and Matsumoto, T., 2001. The Sissano, Papua New Guinea tsunami of July 1998 – Offshore evidence on the source mechanism. Marine Geology, 175(1-4): 1-23. DOI:10.1016/S0025-3227(01)00131-1 (  0) 0) |
Wang, F., Dai, Z., Nakahara, Y., and Sonoyama, T., 2018. Experimental study on impact behavior of submarine landslides on undersea communication cables. Ocean Engineering, 148: 530-537. DOI:10.1016/j.oceaneng.2017.11.050 (  0) 0) |
Watts, P., 1998. Wavemaker curves for tsunamis generated by underwater landslides. Journal of Waterway, Port, Coastal, and Ocean Engineering, 124(3): 127-137. DOI:10.1061/(ASCE)0733-950X(1998)124:3(127) (  0) 0) |
Watts, P., 2000. Tsunami features of solid block underwater landslides. Journal of Waterway, Port, Coastal, and Ocean Engineering, 126(3): 144-152. DOI:10.1061/(ASCE)0733-950X(2000)126:3(144) (  0) 0) |
Wiegel, R. L., 1995. Laboratory studies of gravity waves generated by the movement of a submerged body. Eos, Transactions American Geophysical Union, 36(5): 759-774. DOI:10.1029/TR036I005P00759 (  0) 0) |
Yavari-Ramshe, S., and Ataie-Ashtiani, B., 2017. A rigorous finite volume model to simulate subaerial and submarine landslidegenerated waves. Landslides, 14: 203-221. DOI:10.1007/s10346-015-0662-6 (  0) 0) |
Yeylaghi, S., Moa, B., Buckham, B., Oshkai, P., Vasquez, J., and Crawford, C., 2017. ISPH modelling of landslide generated waves for rigid and deformable slides in Newtonian and non-Newtonian reservoir fluids. Advances in Water Resources, 107: 212-232. (  0) 0) |
Zakeri, A., Høeg, K., and Nadim, F., 2008. Submarine debris flow impact on pipelines – Part Ⅰ: Experimental investigation. Coastal Engineering, 55(12): 1209-1218. DOI:10.1016/j.coastaleng.2008.06.003 (  0) 0) |
Zakeri, A., Høeg, K., and Nadim, F., 2009. Submarine debris flow impact on pipelines – Part Ⅱ: Numerical analysis. Coastal Engineering, 56(1): 1-10. DOI:10.1016/j.coastaleng.2008.06.005 (  0) 0) |
Zhang, G., Chen, J., Qi, Y., Li, J., and Xu, Q., 2022. A WCSPH two-phase mixture model for tsunami waves generated by granular landslides. Computers and Geotechnics, 144: 104657. DOI:10.1016/j.compgeo.2022.104657 (  0) 0) |
Zhang, Y., Wang, Z. T., Yang, Q., and Wang, H. Y., 2019. Numerical analysis of the impact forces exerted by submarine landslides on pipelines. Applied Ocean Research, 92: 101936. DOI:10.1016/j.apor.2019.101936 (  0) 0) |
Zhao, E. J., Dong, Y. K., Tang, Y. Z., and Cui, L., 2021. Numerical study on hydrodynamic load and vibration of pipeline exerted by submarine debris flow. Ocean Engineering, 239: 109754. DOI:10.1016/j.oceaneng.2021.109754 (  0) 0) |
Zhu, G. X., Zou, L., Chen, Z., Wang, A. M., and Liu, M. B., 2018. An improved SPH model for multiphase flows with large density ratios. International Journal for Numerical Methods in Fluids, 86(2): 167-184. DOI:10.1002/fld.4412 (  0) 0) |
 2025, Vol. 24
2025, Vol. 24


