2) Key Laboratory of Unconventional Oil & Gas Development (China University of Petroleum (East China)), Ministry of Education, Qingdao 266580, China
As the water depth of oil and gas development advances, vortex-induced vibration (VIV) is one of the main contributors to the fatigue failure of marine structures. Studies have focused on the structural parameters, fluid parameters, and the arrangements and quantity of marine risers (Liu et al., 2020). VIV control is essential for avoiding fatigue damage to structures. Typically, rotating cylinders can be used to suppress vibration (Hong and Shah, 2018). Strong vibrations are used for energy harvesting in the field of clean wind and water energy (Zhu and Gao, 2017; Raza et al., 2020). Riserless drilling has been typically applied in offshore oil and gas engineering at an early stage of offshore drilling, deep-sea drilling, and scientific drilling, among others (Rheem and Kato, 2011). Riserless drilling technology can reduce the load-bearing capacity of floating drilling devices and drilling costs and can be used to address drilling problems under complex seabed conditions. However, the characteristics of the VIV of the drill string differ from those of the riser because the drill string rotates during operations, and it has complex motion rules and stress distribution (Inoue et al., 2013).
Extensive studies have been conducted on the flow-induced vibration of bluff bodies, and elastically mounted rotating cylinders have attracted considerable attention. The dynamic response of a one-degree-of-freedom (1-DOF) rotating body coupling VIV was first considered. Zhao et al. (2014) investigated the vibration of a rotating circular cylinder at a low Reynolds number. Numerical results revealed that amplitudes increased and that the range of the lock-in region in the cross-flow (CF) direction widened. Two-dimensional and three-dimensional numerical simulation methods were used to analyze the VIV of a cylinder that freely oscillated in the CF direction; the result shows that the vibration amplitude exhibited a bell shape and reached 1.9 times diameter (D), which is three times the maximum amplitude under the nonrotating condition (Bourguet and Jacono, 2014). The VIV of a rotating cylinder in the CF direction was experimentally investigated, and the responses were measured (Seyed-Aghazadeh and Modarres-Sadeghi, 2015). The effects of rotation on the VIV in the CF direction of a sphere were investigated numerically; the dimensionless rotation rate was defined as α (α = ωD/(2U)), with ω and U as the angular velocity and current velocity, respectively. The result revealed that VIV was suppressed completely for α > 1.3 (Rajamuni et al., 2018). Similarly, the 1-DOF rotating cylinder motion constrained to the in-line (IL) direction was also studied, and the wake structure was identified using the particle image velocimetry technique (Zhao et al., 2018).
Few studies have considered the rotation coupling VIV in two-degrees-of-freedom (2-DOF) cylinder motion. Kloven and Huang (2009) studied the VIV responses and motion trajectories of a cylinder early with a dimensionless rotation rate of 0.5-infinity within the reduced velocity range of 3 – 9. The vibration response of the rotating body was closely related to the flow velocity, and it exhibited various dynamic characteristics in distinctly reduced velocities. The response was characterized as VIV at a lower reduced velocity (Ur < 10), and galloping occurred at the highest reduced velocities (Braaten et al., 2007). Rotation can enhance or suppress responses because of the rotating body and the interference characteristics of the flow field. Enhancement and suppression can be used in energy harvesting and vibration control, respectively (Wong et al., 2017). Yu et al. (2015) numerically studied VIV elimination by using a freely rotating fairing and revealed that VIV was completely suppressed at both low and high Reynolds numbers. Large oscillations and nonsymmetric trajectories were observed at a critical Reynolds number. Rotating control cylinders with a reasonable rotation velocity were used to control the vibration of the main cylinder by injecting sufficient momentum into the boundary layer, thus resulting in a 64.56% reduction in the CF direction (Zhu et al., 2015). Furthermore, the gap range of rotating rods is critical; the reattachment of the flow on the leeward side of the main cylinder led to a reasonable and narrow wake, and the vibration was suppressed (Zhu and Gao, 2018). Similarly, Silva-Ortega and Assi (2017) used eight wake-control cylinders to control the VIV of a circular cylinder by changing the rotation speed and diameter of the control cylinders. The rotating cylinders suppressed the peak amplitudes by approximately 70%. In contrast, eight nonrotating control cylinders achieved less than 99% vibration suppression. Nonlinear traveling wave vibrations were studied by Sun et al. (2018), and some complex dynamic characteristics of wave vibrations were revealed. Tumkur et al. (2017) studied a nonlinear energy sink, which consisted of mass rotating cylinders and allowed for vibration in the CF direction only.
The hydrodynamic performance of the rotating cylinder is a complex problem in fluid mechanics. Rotating cylinders find considerable applications in aerospace, energy development, and ocean engineering. Riserless drilling technology presents advantages in marine structures. Few studies have been conducted on the VIV of a 2-DOF rotating cylinder in a uniform flow, and the coupling mechanism of rotation angular velocity and flow velocity remains unclear. Therefore, clarifying the VIV response characteristics in the current of the rotating cylinder is critical. In this study, the flow velocity and the rotation angular velocity before and after the critical rotation angular velocity were used as independent variables. The dynamic response of the 2-DOF cylinder coupling VIV was then studied by using FLUENT fluid simulation software with the user-defined function (UDF) embedded. The dynamic evolution of the cylinder and its flow-field distribution under the variation of the rotation angular velocity were also investigated.
The basic theory of numerical simulations is introduced in Section 2. The numerical simulation processes are presented in Section 3. The simulation conducted in this study is compared with results in the literature on a 2-DOF cylinder and a rotating cylinder in Section 4. In Section 5, the dynamic response (structural displacement, vibration frequency, motion trajectory, etc.) and flow-field distribution of the cylinder were discussed under various rotational angular velocities and flow velocities. Conclusions are presented in Section 6.
2 Numerical Methods 2.1 Flow ModelTwo-dimensional unsteady Reynolds-averaged Navier-Stokes equations and the SST k-ω turbulence model are used to describe the incompressible turbulent current
| $ \frac{{\partial ({{\bar u}_i})}}{{\partial {x_i}}} = 0, $ | (1) |
| $ \rho {\bar u_i}\frac{{\partial ({{\bar u}_i})}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ { - \bar p{\delta _{ij}} + \mu \left({\frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}} + \frac{{\partial {{\bar u}_j}}}{{\partial {x_i}}}} \right) - \rho \overline {{{u'}_i}{{u'}_j}} } \right], $ | (2) |
where
| $ - \overline {{{u'}_i}{{u'}_j}} = {v_t}{S_{ij}} - \frac{2}{3}{\delta _{ij}}k, $ | (3) |
where
| $ {S_{ij}} = \frac{1}{2}(\frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}} + \frac{{\partial {{\bar u}_j}}}{{\partial {x_i}}}), {v_t} = {C_\mu }\frac{{{k^2}}}{\varepsilon }, $ |
in which ui and uj are the velocities along the i and j directions, respectively; vt is the turbulence kinematic viscosity; and ρ and p are the density and pressure, respectively.
The element-based finite volume method and the turbulence model SST k-ω are adopted
| $ \frac{\partial }{{\partial t}}(\rho k) + \frac{\partial }{{\partial {x_i}}}(\rho k{u_i}) = \frac{\partial }{{\partial {x_i}}}\left({{\Gamma _k}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} - {Y_k} + {S_k}, $ | (4) |
| $ \frac{\partial }{{\partial t}}(\rho \omega) + \frac{\partial }{{\partial {x_i}}}(\rho \omega {u_i}) = \frac{\partial }{{\partial {x_i}}}\left({{\Gamma _\omega }\frac{{\partial \omega }}{{\partial {x_j}}}} \right) + {G_\omega } - {Y_\varpi } + {D_\omega } + {S_\omega }, $ | (5) |
where Gk and Gω are the turbulent kinetic energy and the equation for ω, respectively; Гk and Гω are the effective diffusion terms for k and ω, respectively; Yk and Yω are the divergent terms for k and ω, respectively; and Dω, Sk, and Sω are the orthogonal divergence term and custom terms.
2.2 Structural ModelAn elastically supported mass spring damping system is used to ensure equivalent structural vibration, which is depicted in Fig. 1. The vibration control equations of a 2-DOF cylinder considering elastic support are second-order ordinary differential equations
| $ m{\ddot x_{(t)}} + c{\dot x_{(t)}} + k{x_{(t)}} = {F_{D(t)}}, $ | (6) |
| $ m{\ddot y_{(t)}} + c{\dot y_{(t)}} + k{y_{(t)}} = {F_{L(t)}}, $ | (7) |
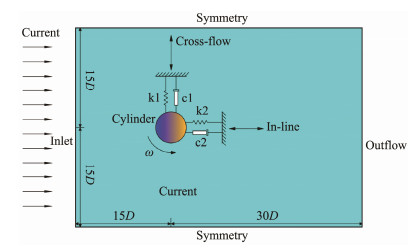
|
Fig. 1 Structural model of the rotating cylinder. |
where m, k, and c are the unit length mass, stiffness coefficient, and damping coefficient, respectively; FD(t) and FL(t) are the lift and drag forces, respectively; and
| $ {F_{L(t)1}} = \frac{1}{2}\rho \dot y_{(t)}^2A{C_{L1}}, $ | (8) |
where ρ is the fluid density, A is the cross-sectional area of the cylinder, and CL1 is the lift coefficient due to the Magnus effect.
2.3 Discrete MethodUniform velocity was set as the boundary condition of the inlet
| $ u = U, {\text{ }}v = 0 . $ | (9) |
Zero gradient for velocity was set as the boundary condition of the outlet
| $ \frac{{\partial u}}{{\partial x}} = 0, \frac{{\partial v}}{{\partial x}} = 0 . $ | (10) |
The boundary conditions of the top and the bottom are specified as a no-slip wall. Thus,
| $ \frac{{\partial u}}{{\partial y}} = 0, v = 0 . $ | (11) |
The no-slip condition is applied on the surface of the rotating cylinder. The initial conditions for the cylinder are
| $ {u_{(0)}} = 0, {\text{ }}{v_{(0)}} = 0, $ | (12) |
| $ {x_{(0)}} = 0, {\text{ }}{y_{(0)}} = 0 . $ | (13) |
The four-step Runge-Kutta method (Zou et al., 2019; Lou et al., 2021) is adopted to discretize and solve Eqs. (6) and (7), and the function f(v, y) is as follows:
| $ f(v, y) = \frac{{{F_{L(t)}}}}{m} - 2\zeta {\omega _0}{\dot y_{(t)}} - \omega _0^2{y_{(t)}} . $ | (14) |
| $ {v_{({t_{n + 1}})}} = {v_{({t_n})}} + \frac{{\Delta t}}{6} \times \left({{K_1} + 2{K_2} + 2{K_3} + {K_4}} \right), $ | (15) |
| $ {y_{({t_{n + 1}})}} = {y_{({t_n})}} + \Delta t \times {v_{({t_n})}} + \frac{{{{(\Delta t)}^2}}}{6} \times ({K_1} + {K_2} + {K_3}), $ | (16) |
in which K1, K2, K3, and K4 are
| $ {K_1} = \frac{{{F_{y(t)}}}}{m} - 2\zeta {\omega _0}{v_{({t_n})}} - \omega _0^2{y_{({t_n})}}, $ | (17) |
| $ {K_2} = \frac{{{F_{y(t)}}}}{m} - 2\zeta {\omega _0}\left({{v_{({t_n})}} + \frac{{\Delta t}}{2} \cdot {K_1}} \right) - \omega _0^2\left({{y_{({t_n})}} + \frac{{\Delta t}}{2} \cdot {v_{({t_n})}}} \right), $ | (18) |
| ${K_3} = \frac{{{F_{y(t)}}}}{m} - 2\zeta {\omega _0}\left({{v_{({t_n})}} + \frac{{\Delta t}}{2} \cdot {K_2}} \right) - \\ \;\;\;\omega _0^2\left({{y_{({t_n})}} + \frac{{\Delta t}}{2} \cdot {v_{({t_n})}} + \frac{{{{\left({\Delta t} \right)}^2}}}{4} \cdot {K_1}} \right), $ | (19) |
| $ {K_4} = \frac{{{F_{y(t)}}}}{m} - 2\zeta {\omega _0}\left({{v_{({t_n})}} + \Delta t \cdot {K_3}} \right) - \\ \;\;\;\omega _0^2\left({{y_{({t_n})}} + \Delta t \cdot {v_{({t_n})}} + \frac{{{{(\Delta t)}^2}}}{2} \cdot {K_2}} \right) . $ | (20) |
The initial conditions are v(t = 0) = v0 and y(t = 0) = y0. Therefore, the calculation method in IL direction is similar to the above.
3 Numerical Description and Solution 3.1 Numerical ParametersThe distance between the inlet and cylinder's center and the distance between two sides of the boundary are all 15.0 D, and the distance between the outlet and cylinder's center is 30.0 D, beyond the influence range of the boundary effect (Prasanth et al., 2006). The mesh density and size of the computing domain obtain a suitable mesh, acceptable computing time, and accurate resolution (Lou et al., 2021). The fluid calculation area is set to the area of 45.0 D × 30.0 D.
The rotating cylinder can vibrate with 2-DOF, and the parameters of spring and damping are the same in two directions. Overlapping mesh technology is adopted in this paper. This technology has lower requirements for mesh topology compared with the traditional mesh and can avoid the negative volume problem that tends to occur during the dynamic update of traditional moving mesh. Thus, high mesh quality can always be maintained during the mesh movement, as shown in Fig. 2. To ensure the reliability of the parameters, the structural parameters such as mass ratio, damping ratio, and mass are based on the experimental results obtained by Wong et al.(2017, 2018). The parameters of the cylinder model are shown in Table 1.
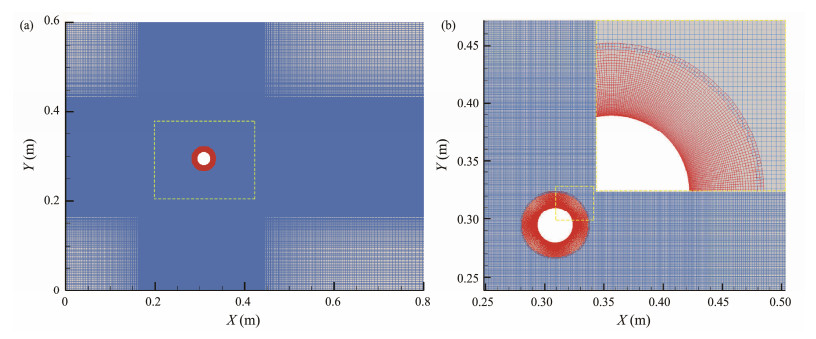
|
Fig. 2 Mesh of the computational domain. (a), overall mesh; (b), mesh near the cylinder. |
|
|
Table 1 Parameters of the cylinder model |
A uniform current is allowed to flow along the X-direction. The velocity is U, the reduced velocity range was 3 – 14, and the Reynolds number range was 1800 – 8400. The riserless drill string is simplified as a cylinder that rotates counterclockwise around the axis. The rotation angular velocities before and after the critical rotation angular velocity were used as independent variables. According to the required rotation velocity of the drill string (Hu et al., 2010), the rotation velocity range was 40 – 120 r min−1, and the corresponding rotation angular velocity ω ranged from 4.19 to 12.57 rad s−1. The specific conditions and the corresponding dimensionless rotation angular velocities are presented in Table 2.
|
|
Table 2 Numerical simulation cases |
The two-dimensional URANS modeling of the fixed riser at Re = 3900 was verified, as shown in Table 3. The comparative analysis shows that the drag coefficient and Strouhal number obtained by the simulation in this paper are in good agreement with existing results (Norberg, 1987; Ong and Wallace, 1996; Franke and Frank, 2002; Cui, 2014; Yang, 2015). The comparison between the calculated results in this paper and those in Chen et al. (2018) is shown in Fig. 3. The simulated frequency ratio fs / f1 and the CF peak amplitude yMax / D are close to the results of the references. Therefore, the calculation results of the flow around the cylinder and the two-dimensional URANS modeling are reliable.
|
|
Table 3 Comparison between the results of this paper and related references |
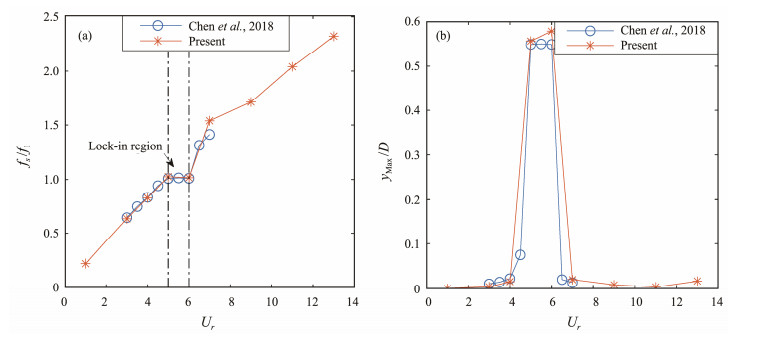
|
Fig. 3 Comparison of calculation results. (a), frequency ratio; (b), peak amplitude. |
The dynamic response of a rotating cylinder coupling VIV is less studied than that of a 2-DOF VIV model. The authors chose the same structural parameters as those used by Zou et al. (2019) and obtained the average dimensionless displacement of the rotating cylinder under the excitation of the current. When the direction of rotation was consistent with the direction of the incoming flow, low pressure was generated on one side of the cylinder, and high pressure was generated on the other side. Fig. 4(a) reveals that the lift of a rotating cylinder increases with the rotation angular velocity, leading to an increased magnitude of average dimensionless displacement, which is consistent with the conclusion obtained by Zou et al. (2019). Few differences are found between the calculation results in this paper and the literature results, and the maximum error in the CF direction is 8.9%, which is within the allowable error range. Thus, the accuracy of the custom function UDF and the reliability of the fluid-structure coupling calculation model are ensured.
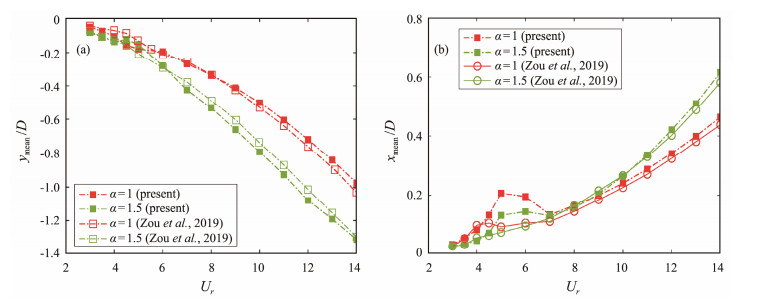
|
Fig. 4 Average dimensionless displacement of the rotating cylinder. (a), CF; (b), IL. |
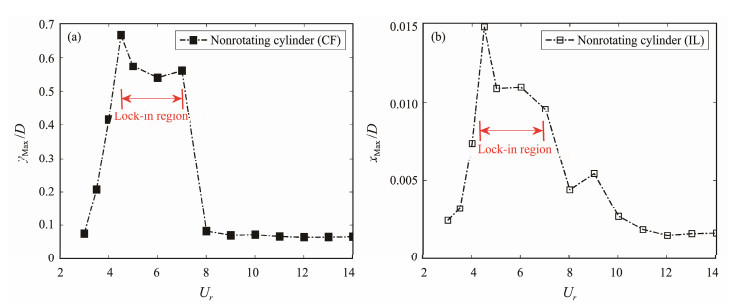
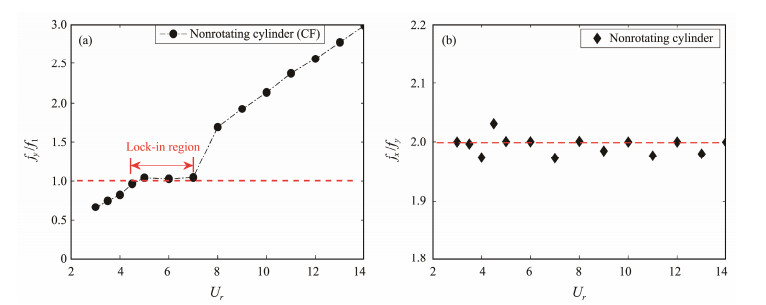
The VIV responses of a nonrotating cylinder with 2-DOF are given. Figs. 5 and 6 show the dimensionless displacement and frequency response of the VIV of a 2-DOF nonrotating cylinder, respectively. Figs. 5(a) and 5(b) present the maximum values of the dimensionless displacements of the cylinder. Fig. 6(a) reveals the variation of the dimensionless dominant frequency fy / f1 of lift versus the reduced velocity, where f1 is the first-order natural frequency obtained from the free attenuation test (Wong et al., 2017, 2018), with a value of 0.671 Hz. The analysis revealed that in the range of 4.5 ≤ Ur ≤ 7, the dimensionless dominant frequency of the lift remained stable, and the vortex shedding frequency of the cylinder was close to its natural frequency. The dimensionless displacement amplitude increased sharply, especially in the CF direction, and the lock-in region was achieved. Fig. 6(b) shows the ratio of dimensionless dominant frequencies in CF and IL directions fluctuates around 2, which is consistent with the findings of other studies (Gao et al., 2015).
|
Fig. 5 Amplitude response of the 2-DOF nonrotating cylinder. (a), CF; (b), IL. |
|
Fig. 6 Frequency response of the 2-DOF nonrotating cylinder. (a), dominant frequency in the CF direction; (b), frequency ratio of IL and CF directions. |
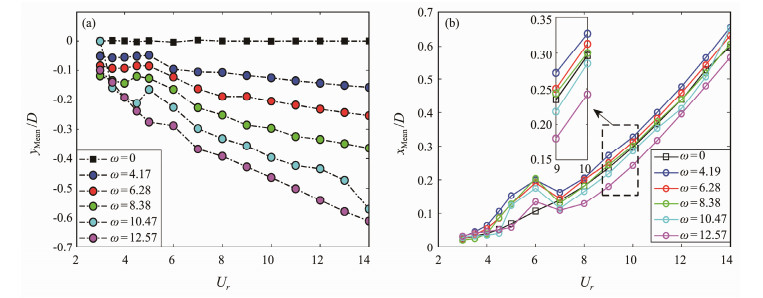
Fig. 7 shows average dimensionless displacements of the cylinder in the CF and IL directions under a uniform current at various rotation angular velocities. In the CF direction, the average dimensionless displacement of the rotating cylinder versus the rotation angular velocity exhibited an increasing trend due to the increased pressure difference between the two sides of the cylinder with the rotation angular velocity. As a result, the Magnus effect became more pronounced. This finding is consistent with the conclusions of Bourguet and Jacono (2014) and Munir et al. (2018).
|
Fig. 7 Average dimensionless displacement of the rotating cylinder at ω = 4.19, 6.28, 8.38, 10.47, and 12.57 rad s−1. (a), CF; (b), IL. |
In the IL direction, the average dimensionless displacements of the rotating cylinder were larger than that of the nonrotating cylinder when ω = 4.19 and 6.28 rad s−1, closest to that of the nonrotating cylinder when ω = 8.38 rad s−1, and lower than that of the nonrotating cylinder when ω = 10.47 and 12.57 rad s−1 in the range Ur ≤ 13. This result indicates that the average dimensionless displacement in the IL direction increased at a certain rotation angular velocity. However, with the continued increase in the rotation angular velocity, the IL dimensionless displacement was suppressed to a certain extent. The overall CF and IL average dimensionless displacements revealed an increasing trend versus reduced velocity but within 4.5 ≤ Ur ≤ 7, the CF average dimensionless displacements appeared to first decrease and then increase; this phenomenon was more pronounced especially in the IL direction. The corresponding range of this phenomenon was the lock-in region of the nonrotating cylinder, during which the VIV influenced the average dimensionless displacement of the rotating cylinder considerably.
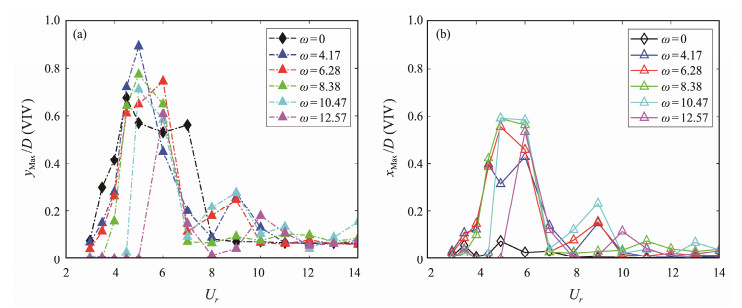
To study the influence of VIV on the dimensionless displacement of the rotating cylinder and eliminate the influence of the Magnus effect and the flow on the initial displacement of the cylinder, Fig. 8 illustrates a comparison of the maximum dimensionless amplitude of the rotating cylinder at the equilibrium position and the nonrotating cylinder.
|
Fig. 8 Maximum dimensionless amplitude of the rotating cylinder at ω = 4.19, 6.28, 8.38, 10.47, and 12.57 rad s−1. (a), CF; (b), IL. |
In the CF direction, for the lower-rotation angular velocity conditions (ω = 4.19, 6.28, and 8.38 rad s−1), the rotating cylinder functioned as a nonrotating cylinder at low reduced velocities. The maximum dimensionless amplitude versus the reduced velocity displayed an increasing trend, and a peak value was reached near the lock-in region of the nonrotating cylinder. The amplitude revealed a downward trend. However, for high-rotation angular velocity conditions (ω = 10.47, 12.57 rad s−1), the maximum dimensionless amplitude was small (in the range of Ur ≤ 4.5), and the dimensionless rotation angular velocity (2–3) of the rotating cylinder was larger than in other conditions, which reveals that the CF amplitude of VIV can be restrained under high nondimensional rotation angular velocities. Moreover, the high-amplitude region became narrower as the rotation angular velocity increased. When Ur ≥ 8, the maximum dimensionless amplitude of the rotating cylinder was larger than that of the nonrotating cylinder. In this range, the dimensionless rotation angular velocity α ≤ 1 can promote the amplitude of VIV.
In the IL direction, the peak values of the maximum dimensionless amplitude corresponding to the conditions of ω = 4.19, 6.28, 8.38, 10.47, and 12.57 rad s−1 were 0.428, 0.557, 0.591, 0.592, and 0.537, respectively. With the increase in the rotation angular velocity, the peak value of the maximum dimensionless amplitude first increased and subsequently decreased. However, under most simulation conditions, the peak value of IL maximum dimensionless amplitude was greater than that of the nonrotating cylinder, especially in the nonrotating cylinder lock-in region (4.5 ≤ Ur ≤ 7). As a result of the Magnus effect, the IL amplitude reached the CF amplitude, which caused a larger variation in the IL amplitude than that in the CF direction.
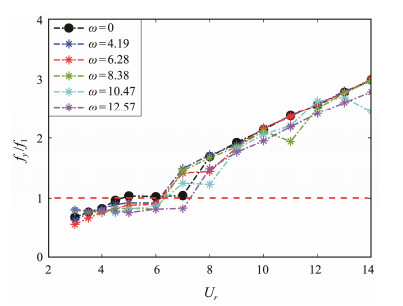
5.1.2 Frequency responseFig. 9 displays the CF dimensionless dominant frequency of the rotating cylinder under uniform incoming flow versus the reduced velocity and reveals the result of a nonrotating cylinder for comparison. At the same reduced velocity, the dimensionless dominant frequency of the rotating cylinder was generally smaller than that of the nonrotating cylinder. At low-rotation angular velocities (ω = 4.19, 6.28 rad s−1), the amplitude and trend of the CF dimensionless dominant frequency of the rotating cylin der were almost the same as those of the nonrotating cylinder. At high-rotation angular velocities (ω = 8.38, 10.47, and 12.57 rad s−1) and low reduced velocities, the trend of the dimensionless dominant frequency of a rotating cylinder differed considerably from that of a nonrotating cylinder.
|
Fig. 9 Dimensionless dominant frequencies of the rotating cylinder in the CF direction at ω = 4.19, 6.28, 8.38, 10.47, and 12.57 rad s−1. |
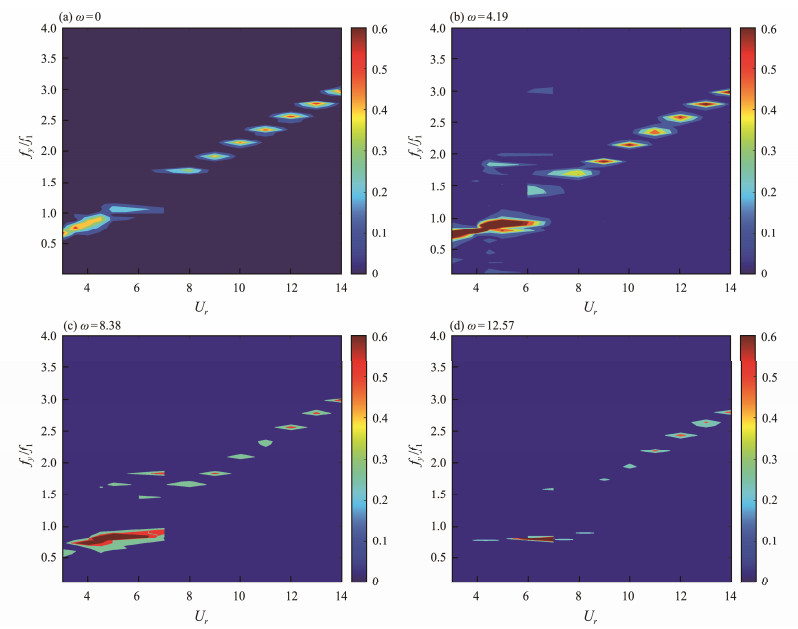
In Fig. 10, the ordinate represents the dimensionless dominant frequency, the abscissa represents the reduced velocity, and the color represents the power spectral density. Figs. 9 and 10 present that the rotating cylinder does not have a definite lock-in region, but a frequency stability region of 0.5 < fy / f1 < 1 is found in the range of 3 ≤ Ur ≤ 8. The dimensionless dominant frequency remained unchanged within this range. Although the frequency stability region of the ω = 12.57 rad s−1 condition was the widest, its vibration intensity was the weakest. Compared with that in nonrotating conditions, the vibration energy accumulation of the rotating cylinder in the stable frequency range was considerable, and the frequency step phenomenon appeared near Ur = 6, revealing high-order harmonic vibration characteristics.
|
Fig. 10 Power spectral density contour of the rotating cylinder (ω = 4.19, 8.38, and 12.57 rad s−1) and nonrotating cylinder (ω = 0) versus the reduced velocity in the CF direction. |
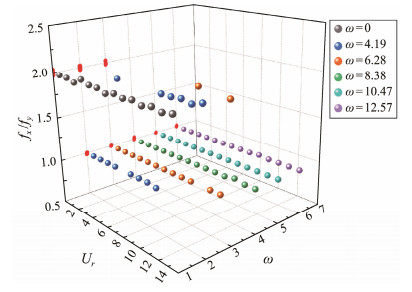
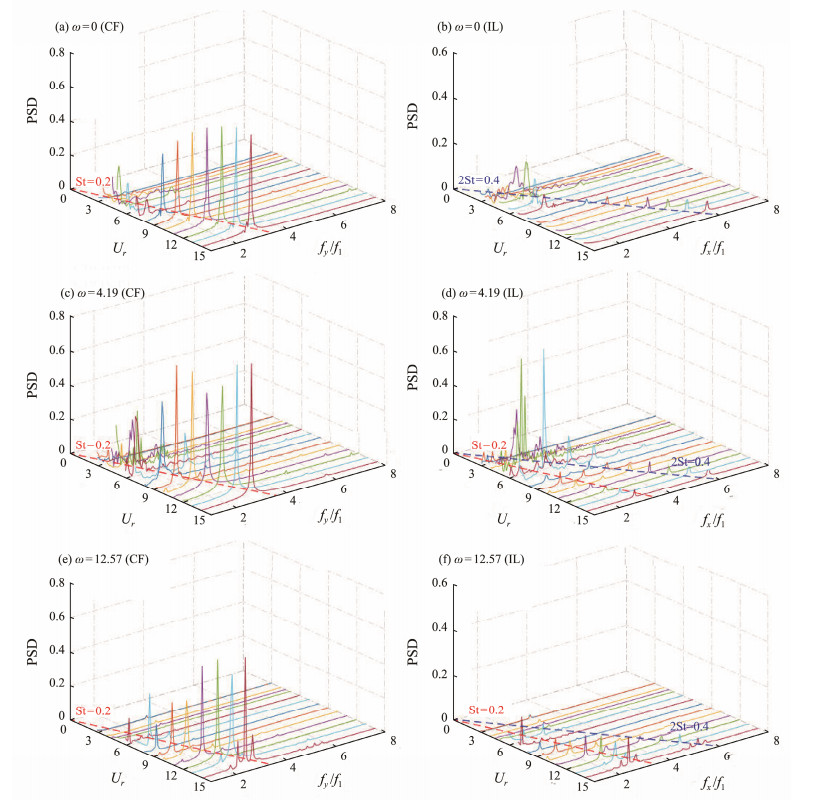
For a nonrotating cylinder under a uniform current, the ratio of the dominant frequency in the IL direction to the CF direction is always 2 (Jiménez-González and Huera-Huarte, 2018; Ma et al., 2020); without a current, this ratio is always 1 (Zou et al., 2019). Fig. 11 displays the ratio of the IL dominant frequency to the CF dominant frequency under uniform flow. The CF dominant frequency of the rotating cylinder is the same as the IL dominant frequency at high-rotation angular velocities (ω = 8.38, 10.47, and 12.57 rad s−1). However, at low-rotation angular velocities (ω = 4.19, 6.28 rad s−1) and higher flow velocities (Ur ≥ 10), the ratio of the dominant frequency in the IL direction to the CF direction is 2 because of the combined action of the forced rotation load and the uniform current. At low-rotation angular velocities (ω = 4.19, 6.28 rad s−1) and higher flow velocities (Ur ≥ 10), the rotating angular velocity was lower than the flow velocity, and the vibration frequency of the rotating cylinder was dominated by VIV, which revealed typical characteristics of VIV. The frequency responses of two extreme-rotation angular velocities (ω = 4.19, 12.57 rad s−1) are presented in Fig. 12 for further analysis of this phenomenon. A comparison of Figs. 12(b), 12(d), and 12(f) reveals that the rotating cylinder has both VIV and rotating Magnus effect under uniform currents and at a highly reduced velocity when ω = 4.19 rad s−1, the power spectral density of VIV exceeds that caused by rotation. In contrast, at ω = 12.57 rad s−1, the VIV frequency in the IL direction is almost suppressed by rotation. Therefore, the ratio of the domi nant frequency is 1.
|
Fig. 11 Dominant frequency ratios of the rotating cylinder at ω = 4.19, 6.28, 8.38, 10.47 and 12.57 rad s−1. |
|
Fig. 12 Frequency responses of the rotating cylinder and nonrotating cylinder versus the reduced velocity in the CF and IL directions. (a) (b), ω = 0; (c) (d), ω = 4.19 rad s−1; (e) (f), ω = 12.57 rad s−1. |
The trajectory could be used to visualize the dynamic response of the structure. Fig. 13 illustrates the trajectories versus the reduced velocity at t = 40 – 55 s; the nonrotating cylinder was provided for comparison, as displayed in Fig. 13(a). The trajectory of the nonrotating cylinder presents a standard figure-eight shape, which appeared because the vibration frequency in the IL direction is twice that in the CF direction, and the CF amplitude differs greatly from that in the IL direction. Kang et al. (2016) and Wang et al. (2021) experimentally observed the typical figure-eight phenomenon in the VIV of a 2-DOF cylinder. Before the lock-in region, the vibration trajectory increased as the reduced velocity increased. In the lock-in region, the CF amplitude suddenly increased, especially when Ur = 5 – 7. The initial CF position of the nonrotating cylinder trajectory was always maintained at y/D = 0, which corresponded to the average dimensionless displacement in Fig. 7(a). Non-rotating conditions can provide a reference for the vibration trajectory of a rotating cylinder. Next, the trajectory coupling rotation effect is discussed in detail.

|
Fig. 13 Trajectories of the rotating cylinder at different rotational angular velocities. |
The vibration trajectories of the cylinder at various rotation velocities are displayed in Figs. 13(b) – (f). The vibration trajectory of the cylinder was not always a figure-eight shape, especially in the region of 4.5 ≤ Ur ≤ 7. The vibration trajectory presented a closed circular ring shape, such as when ω = 4.19 rad s−1 at Ur = 4, because the CF and IL frequencies were equal and the CF and IL dimensionless displacement amplitudes were similar. The cylinder vibration trajectory was unstable in the IL direction when ω = 4.19 rad s−1 at Ur = 5. The IL amplitude was considerably higher than the nonrotating conditions with a periodic elliptical shape. As the reduced velocity increased, the vibration trajectory tended to be stable, and the CF amplitude was generally lower than that of the nonrotating conditions. Trajectories were circular and elliptical shapes at ω = 6.28, 8.38 rad s−1, and flat figure-eight vibration trajectories appeared at Ur = 12–14 at the two rotation angular velocities, which differed from that of the ω = 4.19 rad s−1. When the rotation angular velocity increased, the amplitudes in the two directions were close. As the reduced velocity and rotation angular velocity increased, the centroid of the forced rotating cylinder's trajectory deviated from the initial position (x/D = 0, y/D = 0). The former (trajectory deviated from x/D = 0) was the initial position caused by the increase in the flow velocity and the latter (trajectory deviated from y/D = 0) was due to the Magnus effect. The trend is consistent with the average dimensionless displacement result in Fig. 7.
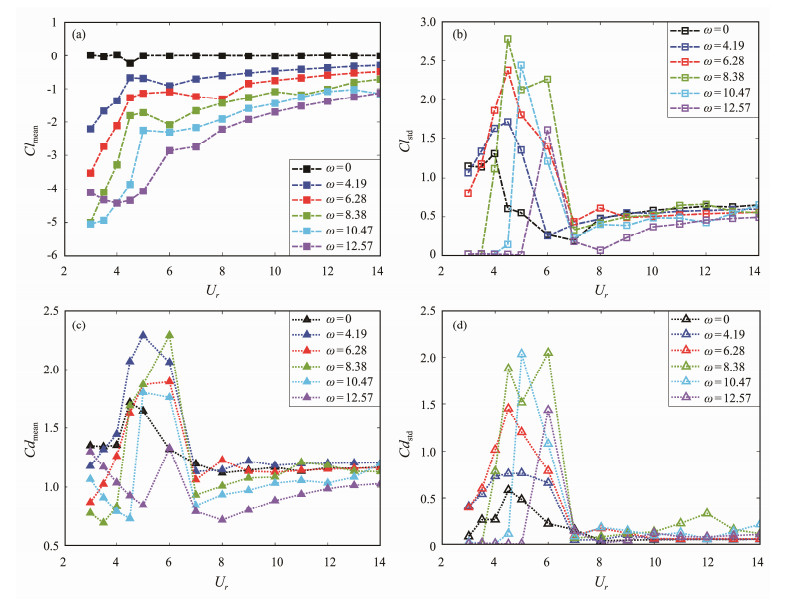
5.2 Flow-Field Analysis 5.2.1 Lift and drag coefficientsFig. 14 illustrates the average lift and drag coefficients (Clmean, Cdmean) and the standard deviation of the lift and drag coefficients (Clstd, Cdstd) versus reduced velocity. The average value of lift and drag coefficients can reflect the characteristics under the combined effect of rotation and VIV. Standard deviation can describe the degree of data deviation from the average value, and the degree of dispersion reflects the amplitude variation of VIV.
|
Fig. 14 Lift and drag coefficients. (a) (c), average value; (b) (d), standard deviation. |
As shown in Fig. 14(a), the mean lift coefficient (Clmean) of the nonrotating cylinder under the uniform flow is maintained at 0. As a result of the Magnus effect, the absolute value of the average lift coefficient of the rotating cylinder is considerably greater than that of the nonrotating cylinder and is larger at reduced velocities. At all reduced velocities when ω = 4.19, 6.28, 8.38, and 10.47 rad s−1, the average lift coefficient increases with the rotation angular velocity; at the same rotation angular velocity, the average lift coefficient first increases and subsequently decreases in the lock-in region of the nonrotating cylinder. Simultaneously, as shown in Fig. 14(b), the standard deviation of the lift coefficient (Clstd) increases with the reduced velocity and reaches the maximum value at Ur = 4.5 (ω = 4.19, 6.28, 8.38 rad s−1), Ur = 5 (ω = 10.47 rad s−1), and Ur = 6 (ω = 12.57 rad s−1), which were within the lock-in region of the nonrotating cylinder. Khalak and Williamson (1999) and Munir et al. (2018) observed the maximum Clstd between the initial branch and the upper branch in free vibration experiments, and the maximum value was observed at Ur = 4 of the nonrotating cylinder in this study. At the upper and lower branch boundaries for the low-mass damping system, Khalak and Williamson (1999) revealed that the phase difference between the lift coefficient and the displacement varies from 0˚ to 180˚ (Fig. 14(b)). This variation in phase corresponded to a considerable reduction in the standard deviation of the lift coefficient.
Figs. 14(c) and 14(d) reveal that the drag coefficient is closer to the nonrotating cylinder at a low-rotation angular velocity, and the mean and standard deviation of the drag coefficient of the rotating cylinder reached the peak value in the lock-in region of the nonrotating cylinder. The high-amplitude vibration increased the resistance. In the range of Ur ≥ 8, the average value of the drag coefficient increased gradually, and the ascent speed versus the reduced velocity decreased gradually, stabilized, and moved closer to the nonrotating cylinder. When ω = 8.38, 10.47, and 12.57 rad s−1, in the ranges of Ur ≤ 3.5, Ur ≤ 4.5, and Ur ≤ 5, the average drag coefficient decreased versus reduced velocity, and the drag coefficient of ω = 12.57 rad s−1 was lower than that in the nonrotating condition. Similar to the standard deviation of the lift coefficient, when the cylinder was subjected to a single-frequency harmonic external load, the phase between the displacement and the force of the cylinder can be 0˚ or 180˚, and the coefficient standard deviation exhibited the largest decrease at the lower boundary of the lock-in region.
5.2.2 Near-wake structureFig. 15 displays the vorticity of the rotating cylinder wake vortices at various rotation angular velocities. The equivalent vorticity values are marked with contour lines in the diagram, and the scale was limited to the range of [−5, 5]. First, a nonrotating condition was compared (Fig. 15(a)). For the rotating cylinder, the wake vorticity diagram revealed that at a relatively low-rotation angular velocity, two counter-rotating vortices fall off in each period, and the wake deflects marginally to the positive direction of the Y-axis, as displayed in Figs. 15(b) and 15(c). In essence, the deflection of the wake was caused by the asymmetry of the lift caused by the Magnus effect. The rotation resulted in the asymmetry of positive and negative eddy current strength and the upward deviation of wake flow (Mittal and Kumar, 2003).
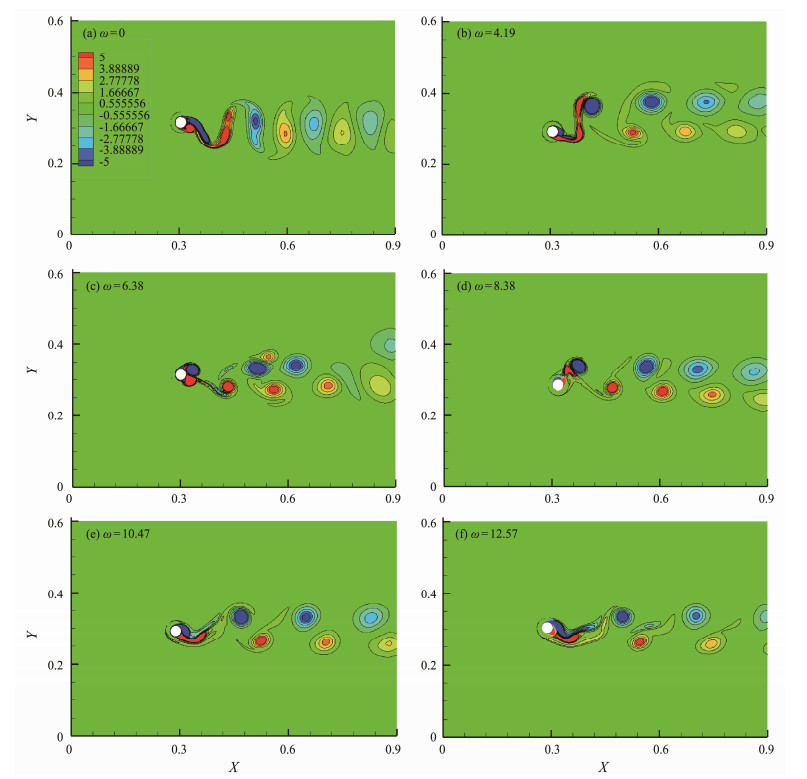
|
Fig. 15 Near-wake structure of the rotating cylinder at Ur = 6. |
To study the near-wake structure of a rotating cylinder versus the rotation angular velocity, Figs. 16(a) – (c) display how the vorticity contour image versus the reduced velocity changed, with ω = 12.57 rad s−1 taken as an example. For high-rotation angular velocity and low reduced velocity, the wake width was narrow and no vortex shedding occurred from the cylinder, which corresponded to the U-shaped wake (Bourguet and Jacono, 2014). The U-shaped wake itself will lead to a large amplitude. However, because no vortex shedding occurs, a small amplitude is caused by VIV, which is consistent with the conclusion in Fig. 8. Typically, U-shaped wakes generally appear at higher nondimensional rotation angular velocities for a rotating cylinder.
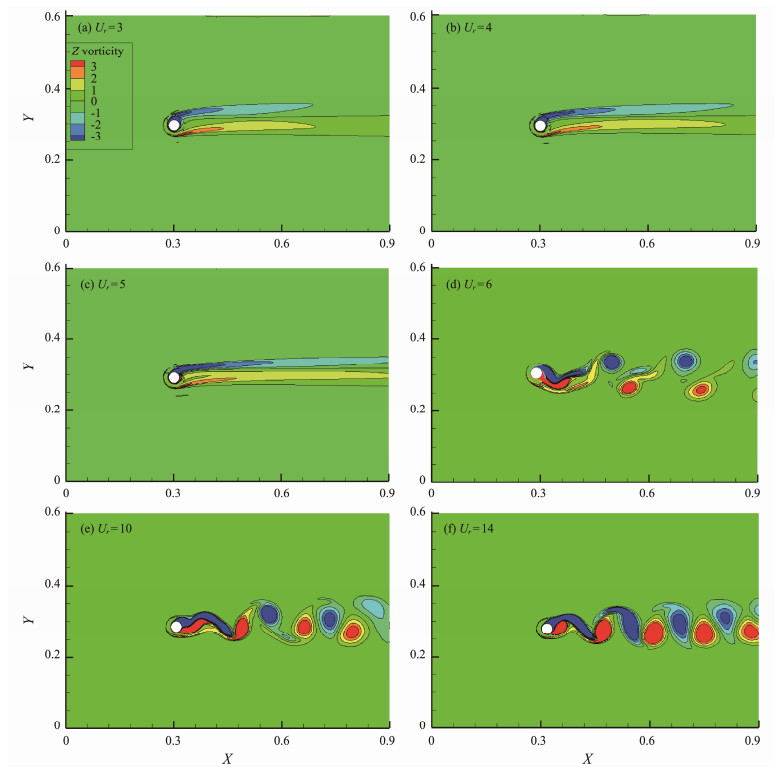
|
Fig. 16 Near-wake structure of the rotating cylinder at ω = 12.57 rad s−1. (a), Ur = 3; (b), Ur = 4; (c), Ur = 5; (d), Ur = 6; (e), Ur = 10; (f), Ur = 14. |
At high reduced velocities (Ur ≥ 6), the vortex mode changed to 2S (Gabbai and Benaroya, 2005). First, one vortex (S) fell off the cylinder, another vortex (S) was generated, and two vortices (2S) were separated from the surface of the rotating cylinder. As the reduced velocity increased gradually, the vortex shedding steadily became regular and gradually moved closer to the nonrotating cylinder vortex shedding mode. However, the difference was that the nonrotating cylindrical wake had a wider range. In contrast, the vortex shedding was compact and the wake width was narrow under the condition of the rotating angular velocity. This feature became obvious as the reduced velocity increased.
6 ConclusionsThe dynamic response of a 2-DOF rotating cylinder coupling VIV was simulated numerically based on the UDF program. The dynamic response of the drill string without a riser under various rotation angular velocities, such as vibration frequency, displacement, vibration trajectory, force coefficient, and vortex off mode, is obtained. The conclusions are as follows:
1) Under uniform flow, the nonrotating cylinder is always in the equilibrium position to generate self-excited and self-limiting periodic vibrations. As a result of the Magnus effect, the CF average dimensionless displacement of the rotating cylinder increases with the rotation angular velocity, whereas the IL average dimensionless displacement decreases versus rotation angular velocity. The upper and lower branches of the VIV are visible in the CF amplitude response of the rotating cylinder. At high dimensionless rotation angular velocities, the CF amplitude of VIV is suppressed, whereas it is promoted at lower dimensionless rotation angular velocities.
2) Rotation causes the CF vibration frequency to be equal to the IL vibration frequency, and the IL displacement approaches the CF displacement. In addition, the Magnus effect has a greater influence on the IL displacement than on the CF displacement. However, for the higher reduced velocity with low-rotation angular velocity conditions, the vibration frequency of the rotating cylinder is dominated by the VIV, and typical VIV characteristics appear.
3) The vibration trajectory of the rotating cylinder deviates from the figure-eight shape and tends to be oval or circular. The wake of the cylinder is deflected in the CF direction because of the asymmetry of the lift caused by the forced rotation. 2S and U-shaped vortices are obtained in the wake structure of the rotating cylinder. VIV is suppressed because no vortex shedding occurs behind the cylinder at high-rotation angular velocities with low reduced velocities.
AcknowledgementsThis work was supported by the National Natural Science Foundation of China (No. U2006226), and the National Key Research and Development Program of China (No. 2016YFC0303800).
Bourguet, R., and Lo Jacono, D., 2014. Flow-induced vibrations of a rotating cylinder. Journal of Fluid Mechanics, 740: 342-380. DOI:10.1017/jfm.2013.665 (  0) 0) |
Braaten, H., Lie, H., Soreide, M., and Svardal, S., 2007. Galloping 2D tests of a two cylinder bundle. ASME 2007 26th International Conference on Offshore Mechanics and Arctic Engineering. San Diego, California: 771-780. (  0) 0) |
Chen, D. Y., Abbas, L. K., Wang, G. P., Rui, X. T., and Marzocca, P., 2018. Numerical study of flow-induced vibrations of cylinders under the action of nonlinear energy sinks (NESs). Nonlinear Dynamics, 94(2): 925-957. DOI:10.1007/s11071-018-4402-z (  0) 0) |
Cui, X. N., 2014. Hydrodynamic characteristics of viscous flow past two side-by-side cylinders. Master thesis. Ocean University of China (in Chinese).
(  0) 0) |
Fleming, P. D., and Probert, S. D., 1984. The evolution of wind-turbines: An historical review. Applied Energy, 18: 163-177. DOI:10.1016/0306-2619(84)90007-2 (  0) 0) |
Franke, J., and Frank, W., 2002. Large eddy simulation of the flow past a circular cylinder at Re = 3900. Journal of Wind Engineering and Industrial Aerodynamics, 90(10): 1191-1206. DOI:10.1016/S0167-6105(02)00232-5 (  0) 0) |
Gabbai, R. D., and Benaroya, H., 2005. An overview of modeling and experiments of vortex-induced vibration of circular cylinders. Journal of Sound and Vibration, 282: 575-616. DOI:10.1016/j.jsv.2004.04.017 (  0) 0) |
Gao, Y., Fu, S. X., Ren, T., Xiong, Y. M., and Song, L. J., 2015. VIV response of a long flexible riser fitted with strakes in uniform and linearly sheared currents. Applied Ocean Research, 52: 102-114. DOI:10.1016/j.apor.2015.05.006 (  0) 0) |
Hong, K. S., and Shah, U. H., 2018. Vortex-induced vibrations and control of marine risers: A review. Ocean Engineering, 152: 300-315. DOI:10.1016/j.oceaneng.2018.01.086 (  0) 0) |
Hu, Y., Di, Q., Wang, W., Yao, J., and Yao, Y., 2010. Influence of rotary table speed on the dynamic characteristics of drillsting in inclined straight hole. Engineering Mechanics, 27: 184-190. (  0) 0) |
Inoue, T., Rheem, C. K., Kyo, M., Sakaguchi, H., and Matsuo, M. Y., 2013. Experimental study on the characteristics of VIV and whirl motion of rotating drill pipe. ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering. Nantes.
(  0) 0) |
Jiménez-González, J. I., and Huera-Huarte, F. J., 2018. Vortex-induced vibrations of a circular cylinder with a pair of control rods of varying size. Journal of Sound and Vibration, 431: 163-176. DOI:10.1016/j.jsv.2018.06.002 (  0) 0) |
Kang, Z., Ni, W. C., and Sun, L. P., 2016. An experimental investigation of two-degrees-of-freedom VIV trajectories of a cylinder at different scales and natural frequency ratios. Ocean Engineering, 126: 187-202. DOI:10.1016/j.oceaneng.2016.08.020 (  0) 0) |
Khalak, A., and Williamson, C., 1999. Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. Journal of Fluids and Structures, 13: 813-851. DOI:10.1006/jfls.1999.0236 (  0) 0) |
Kloven, A., and Huang, S., 2009. Motion response of a rotating cylinder in currents. ASME 2009 28th International Conference on Ocean, Offshore and Arctic Engineering. Honolulu, Hawaii.
(  0) 0) |
Liu, G. J., Li, H. Y., Qiu, Z. Z., Leng, D. X., Li, Z. X., and Li, W. H., 2020. A mini review of recent progress on vortex-induced vibrations of marine risers. Ocean Engineering, 195: 106704. DOI:10.1016/j.oceaneng.2019.106704 (  0) 0) |
Lou, M., Wang, Y., Qian, G. W., and Dong, W. Y., 2021. Investigation on the vortex-induced vibration active control of the riser in the 'lock-in' region based on adaptive fuzzy sliding mode theory. Ocean Engineering, 238: 109697. DOI:10.1016/j.oceaneng.2021.109697 (  0) 0) |
Ma, Y., Xu, W., Pang, T., Wang, Q., and Lai, J., 2020. Dynamic characteristics of a slender flexible cylinder excited by concomitant vortex-induced vibration and time-varying axial tension. Journal of Sound and Vibration, 485: 115524. DOI:10.1016/j.jsv.2020.115524 (  0) 0) |
Mittal, S., and Kumar, B., 2003. Flow past a rotating cylinder. Journal of Fluid Mechanics, 476: 303-334. DOI:10.1017/S0022112002002938 (  0) 0) |
Munir, A., Zhao, M., Wu, H., Lu, L., and Ning, D. Z., 2018. Three-dimensional numerical investigation of vortex-induced vibration of a rotating circular cylinder in uniform flow. Physics of Fluids, 30(5): 053602. DOI:10.1063/1.5025238 (  0) 0) |
Norberg, C., 1987. Effects of Reynolds number and a low-intensity freestream turbulence on the flow around a circular cylinder. Technical report. Chalmers University of Technology, Goteborg, Publikation Nr 87/2, 54pp.
(  0) 0) |
Ong, L., and Wallace, J., 1996. The velocity field of the turbulent very near wake of a circular cylinder. Experiments in Fluids, 20(6): 441-453. DOI:10.1007/BF00189383 (  0) 0) |
Prasanth, T. K., Behara, S., Singh, S. P., Kumar, R., and Mittal, S., 2006. Effect of blockage on vortex-induced vibrations at low Reynolds numbers. Journal of Fluids and Structures, 22: 865-876. DOI:10.1016/j.jfluidstructs.2006.04.011 (  0) 0) |
Rajamuni, M. M., Thompson, M. C., and Hourigan, K., 2018. Vortex-induced vibration of a transversely rotating sphere. Journal of Fluid Mechanics, 847: 786-820. DOI:10.1017/jfm.2018.309 (  0) 0) |
Raza, S. A., Chern, M.-J., Susanto, H., and Zhou, Y.-H., 2020. Numerical investigation of the effects of a small fixed sphere in tandem arrangement on VIV of a sphere. Journal of Wind Engineering and Industrial Aerodynamics, 206: 104368. DOI:10.1016/j.jweia.2020.104368 (  0) 0) |
Rheem, C., and Kato, K., 2011. A basic research on the VIV response of rotating circular. ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering. Rotterdam.
(  0) 0) |
Seyed-Aghazadeh, B., and Modarres-Sadeghi, Y., 2015. An experimental investigation of vortex-induced vibration of a rotating circular cylinder in the crossflow direction. Physics of Fluids, 27(6): 067101. DOI:10.1063/1.4921683 (  0) 0) |
Silva-Ortega, M., and Assi, G. R. S., 2017. Suppression of the vortex-induced vibration of a circular cylinder surrounded by eight rotating wake-control cylinders. Journal of Fluids and Structures, 74: 401-412. DOI:10.1016/j.jfluidstructs.2017.07.002 (  0) 0) |
Sun, S., Liu, L., and Cao, D., 2018. Nonlinear travelling wave vibrations of a rotating thin cylindrical shell. Journal of Sound and Vibration, 431: 122-136. DOI:10.1016/j.jsv.2018.05.042 (  0) 0) |
Tumkur, R. K. R., Pearlstein, A. J., Masud, A., Gendelman, O. V., Blanchard, A. B., Bergman, L. A., et al., 2017. Effect of an internal nonlinear rotational dissipative element on vortex shedding and vortex-induced vibration of a sprung circular cylinder. Journal of Fluid Mechanics, 828: 196-235. DOI:10.1017/jfm.2017.504 (  0) 0) |
Wang, Y., Li, P., Liu, Y., Guo, H. Y., and Lou, M., 2021. Experimental investigation on the vortex-induced vibration of a three-riser group coupling interference effect. Journal of Sound and Vibration, 491: 115740. DOI:10.1016/j.jsv.2020.115740 (  0) 0) |
Wong, K. W. L., Zhao, J., Lo Jacono, D., Thompson, M. C., and Sheridan, J., 2017. Experimental investigation of flow-induced vibration of a rotating circular cylinder. Journal of Fluid Mechanics, 829: 486-511. DOI:10.1017/jfm.2017.540 (  0) 0) |
Wong, K. W. L., Zhao, J., Lo Jacono, D., Thompson, M. C., and Sheridan, J., 2018. Experimental investigation of flow-induced vibration of a sinusoidally rotating circular cylinder. Journal of Fluid Mechanics, 848: 430-66. DOI:10.1017/jfm.2018.379 (  0) 0) |
Yang, Z., 2015. Numerical simulation of cylinder vortex-induced vibration using RANS. Master thesis. Tianjin university (in Chinese).
(  0) 0) |
Yu, Y., Xie, F. F., Yan, H. M., Constantinides, Y., Oakley, O., and Karniadakis, G. E., 2015. Suppression of vortex-induced vibrations by fairings: A numerical study. Journal of Fluids and Structures, 54: 679-700. DOI:10.1016/j.jfluidstructs.2015.01.007 (  0) 0) |
Zhao, J., Lo Jacono, D., Sheridan, J., Hourigan, K., and Thompson, M. C., 2018. Experimental investigation of in-line flow-induced vibration of a rotating circular cylinder. Journal of Fluid Mechanics, 847: 664-699. DOI:10.1017/jfm.2018.357 (  0) 0) |
Zhao, M., Cheng, L., and Lu, L., 2014. Vortex induced vibrations of a rotating circular cylinder at low Reynolds number. Physics of Fluids, 26(7): 073602. DOI:10.1063/1.4886196 (  0) 0) |
Zhu, H. J., and Gao, Y., 2017. Vortex induced vibration response and energy harvesting of a marine riser attached by a free-to-rotate impeller. Energy, 134: 532-544. DOI:10.1016/j.energy.2017.06.084 (  0) 0) |
Zhu, H. J., and Gao, Y., 2018. Effect of gap on the vortex-induced vibration suppression of a circular cylinder using two rotating rods. Ships and Offshore Structures, 13: 119-131. DOI:10.1080/17445302.2017.1328756 (  0) 0) |
Zhu, H. J., Yao, J., Ma, Y., Zhao, H. N., and Tang, Y. B., 2015. Simultaneous CFD evaluation of VIV suppression using smaller control cylinders. Journal of Fluids and Structures, 57: 66-80. DOI:10.1016/j.jfluidstructs.2015.05.011 (  0) 0) |
Zou, Q. F., Ding, L., Wang, H. B., Wang, J. L., and Zhang, L., 2019. Two-degree-of-freedom flow-induced vibration of a rotating circular cylinder. Ocean Engineering, 191: 106505. DOI:10.1016/j.oceaneng.2019.106505 (  0) 0) |
 2023, Vol. 22
2023, Vol. 22


