2) Marine Resources and Environment Research Group on the Maritime Silk Road, Dalian 116018, China;
3) Dalian Naval Academy, Dalian 116018, China;
4) State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics (LASG), Institute of Atmospheric Physics, The Chinese Academy of Sciences, Beijing 100029, China
The overexploitation of traditional resources, such as coal, oil, and natural gas, has led to three global crises: resource shortage, environmental pollution, and ecological devastation. The development of renewable energy plays an important role in meeting the growing demand for energy. At present, the development of new energy sources, such as solar and wind energy, has become the focus of attention of domestic and foreign scholars. However, high temperature, high humidity, high salt, and other complex ocean conditions affect the conversion and exploitation of solar energy. Offshore wind power is widely distributed; however, it suffers from high cost, difficulty of grid power, and other problems. In addition, the ocean area accounts for more than 70% of the total area of the earth, and the ocean is rich in natural resources, including marine, mineral, and energy resources. Wave energy is one of the most promising ocean energy resources, and it has become the darling of the new era because of its abundant reserves and nonpollution. The study area is located around SL waters, which is a cricial area of the 21st Century Maritime Silk Road. Located southeast of SL is the important Strait of Malacca; situated northwest is the Persian Gulf and the Gulf of Aden. Moreover, SL is located in a pivotal region of the Indian Ocean, which also has a vital strategic position by guarding the channel of oil output from the Persian Gulf to the east.
Chen et al. (2002) found three tongue swell pools, which are located in the Atlantic Ocean, the Pacific Ocean, and the tropical waters of the Indian Ocean. The main body of the southern Indian Ocean westerly swells spread to SL waters, whereas the small branch propagates to the Christmas Island waters (Semedo et al., 2011; Zheng and Li, 2017). In addition, they calculated the swell index of the global ocean and found that the swell index in tropical waters of low latitudes is at a high level all year round, confirming the fact that the swell dominates the mixed waves. Bhowmick et al. (2011) found that monsoons and tropical cyclones have a remarkable impact on the propagation of swells in the southern Indian Ocean; they also confirmed that swells spread to the Arabian Sea and the Bay of Bengal. Zheng et al. (2013b) determined the global ocean dominated by swells under the energy balance of wave fields. Previous studies have analyzed the causes of the formation of wave energy but have not provided a detailed assessment of wave energy reserves and have not analyzed the seasonal and regional distribution characteristics of wave energy in SL. Thus, the seasonal of swell propagation from the seasonal distribution differences of wave energy must be verified. In this study, the thirdgeneration wave model WAVEWATCH-Ⅲ (WW3) driven by ERA-Interim wind field was utilized to analyze the seasonal and regional distribution of wave energy resources in SL waters. Moreover, the dominant season that contributes most to total wave power was determined. The exploitation of wave energy provides not only a detailed reference material for the current situation of wave energy but also guidance for disaster prevention and mitigation and coastal management and development at critial area in the future. The bathymetric topographic map of SL waters is shown in Fig.1.
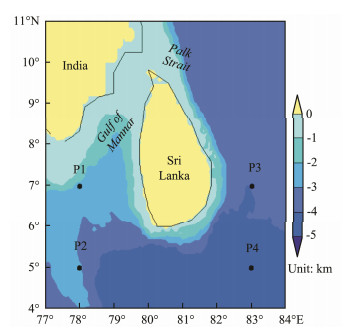
|
Fig. 1 Bathymetric topographic map of SL waters. |
WW3 is one of the most popular wave numerical models and is a popular option for evaluation of marine waves. Many experts and scholars have studied the distribution of wave energy resources through the WW3 model, and they made tremendous contributions to the development of wave energy. Zheng et al. (2016) used WW3 to design a short-term wave energy forecasting structure and found that the China Sea would generate abundant wave energy under the influence of cold air. Soares et al. (2014) used WW3 and SWAN simulation data to evaluate the wave energy along the Atlantic European coast in detail. Wang et al. (2018) once used WW3 to study the reserves and the long-term of wind and wave energy in the South China Sea. Zheng et al. (2013a) and Zheng and Li (2015) analyzed the long-term variation of the WPD and SWH, and assessed the wave energy using WW3 simulated data. Bento et al. (2015) used the coupling model of SWAN and WW3 to describe the wave conditions of the Galway Bay and evaluate its wave energy reserves. This paper used the WW3 simulated wave model to analyze the seasonal and regional distribution of wave energy in SL waters. Then, the seasons and optimum areas with the most abundant wave energy are identified. The rest of this paper is organized as follows: Section 2 introduces the available data and methodology and model validation. Section 3 analyzes the distribution of SWH and WPD. Section 4 shows the analysis results of available SWH and rich WPD. Sections 5 and 6 analyze the contribution and stability of wave energy. Lastly, some important conclusions are summarized.
2 Data and Methodology 2.1 Available DataThis study used two kinds of data sources, including ERA-Interim reanalysis wind field data and the observational data of Jason-2 satellite altimeter. ERA-Interim is a global atmospheric reanalysis that has been available from January 1, 1979 to August 31, 2019 and is the ECM- WF to manage and update the latest global atmospheric numerical data (Aarnes et al., 2015; Taszarek et al., 2018). ERA-Interim shows multiple improvements in the measurement of data, the incorporation of four-dimension variational data assimilation approach, the increase in system resolution, or the enhancement of forecast system physics (Ulazia et al., 2017; Gopalakrishnan et al., 2019; Marcos et al., 2019). Meanwhile, Jason-2 is a joint satellite program between the National Aeronautics and Space Administration and the Center National d'Etudes Spatiales, flying at an identical orbit altitude with an inclination angle of 66˚ and a period of 112 min (Idris et al., 2017; Liu et al., 2018). To reflect real sea conditions accurately, the scientific objectives of Jason-2 include improving the measure of the time averaged ocean circulation and the measure of global sea-level change. Additionally, the spatial range of the altimeter data is 4˚–11˚N, 77˚–84˚E. The spatial resolution is 1˚×1˚. The time range is from January 1, 2017 to December 31, 2017.
2.2 Methodology and Model 2.2.1 Model validationWW3 is the third-generation of full-spectrum space wave models and is developed at the Marine Modeling and Analysis Branch of the Environmental Modeling Center of the National Centers for Environmental Prediction (Tolman, 1991; Langodan et al., 2016). It further improves control equation, program structure, and numerical and physical processing methods on the basis of the WAM model. The model solves the spectral action balance equation and directly calculates the nonlinear energy interaction of different frequency waves. It is especially suitable for long time horizons and regional scale modeling (Uihlein and Magagna, 2016; Lavidas and Venugopal, 2018). The balance equation of wave propagation can be defined as follows:
| $\frac{{\operatorname{d} N(k, \theta)}}{{\operatorname{d} t}} = \frac{{S(k, \theta)}}{\sigma }, $ | (1) |
where N(k, θ) ≡ F(k, θ)/σ represents the wave action density spectrum, which is obtained by the conversion of the wave number direction spectrum N(k, θ); σ is intrinsic frequency; k and θ represent wave number and wave direction, respectively; S represents the source's net effect, which generally contains linear input term Sln, wind-wave interaction term Sin, dissipation term Sds, and wave-bottom interaction term Sbot. S can be defined as follows:
| $S = {S_{{\rm{ln}}}} + {S_{{\rm{in}}}} + {S_{{\rm{ds}}}} + {S_{{\rm{bot}}}}.$ | (2) |
To verify the precision of WW3 simulated wave data, the correlation coefficient (CC), the Bias, and the root mean square error (RMSE) of SWH were calculated on the basis of WW3 simulated data and observed data from Jason-2 satellite altimeter. The formulas involved are as follows:
| $CC{\rm{ = }}\frac{{\sum\nolimits_{i = 1}^n {({x_i} - \bar x)} ({y_i} - \bar y)}}{{\sqrt {{{\sum\nolimits_{i = 1}^n {({x_i} - \bar x)} }^2}\sum\nolimits_{i = 1}^n {{{({y_i} - \bar y)}^2}} } }}, $ | (3) |
| $RMSE = \sqrt {\frac{1}{N}\sum\nolimits_{i = 1}^n {{{({y_i} - {x_i})}^2}} }, $ | (4) |
| $Bias = {y_i} - {x_i}, $ | (5) |
where xi represents the observed SWH; yi represents the simulated SWH;
As shown in Table 1, the Bias of four reference points does not exceed 0.210 m, and their minimum value is 0.046 m. The CCs are generally around 0.9. In summary, the simulated data of WW3 are close to the observed data of the satellite altimeter. The WW3 model is suitable for wave field simulation in the North Indian Ocean. Samiksha et al. (2012) used the WW3 model to analyze the propagation characteristics of Indian Ocean swells.
|
|
Table 1 Parameters of four reference points |
The southern Indian swells propagate northward to the Bay of Bengal and the waters off SL all year round and contribute to the wave height of the northern Indian Ocean. Samiksha et al. (2012) analyzed the propagation characteristic of Indian Ocean swells. They set the study area from latitudes 60˚S to 30˚N and from longitudes 15˚E to 120˚E. The paper have conducted four nested schemes for the WW3 model by taking the southern boundary up to 70˚S. In four schemes, keeping the nested region was set to the west of 30˚E, the north of 30˚N, and the east of 130˚E; the southern boundary was set as 40˚S, 50˚S, 60˚S, and 70˚S in turn. When the southern boundary was set to 60˚S or 70˚S, the SWH not found any change.
To analyze the accuracy of four simulated schemes, the Bias, CC, and RMSE at each grid point was computed by the model-simulated SWH and the measured SWH of the altimeter. Then, the average value of the Bias, CC, and RMSE of the entire region was calculated, as shown in Table 2. With the expansion of the nested region, the Bias and RMSE decrease gradually, and the CC increases continuously. When the southern boundary is set to 60˚S or 70˚S, the Bias, RMSE, and CC remain unchanged. Given the full consideration of swell components, the wave parameters in the study area do not change, thus proving the rationality of the last two schemes.The comparision of the simulated SWH and the ovserved SWH, as shown in Fig.2. In addition, Zhang et al. (2018) assessed the wave energy resources in the global ocean and found that WPD in most sea areas of SL is basically above 2 kW m−1. WPD in the southern sea area is the largest, and its maximum value is greater than 12 kW m−1. When the south nested boundary is set as 60˚S or 70˚S, the spatial distribution of WPD is basically the same, as shown in Fig.3 and Fig.4. The above analysis shows that the south nested boundary set to the south of 60˚S can achieve accurate wave energy evaluation.
|
|
Table 2 Precision of simulated SWH |
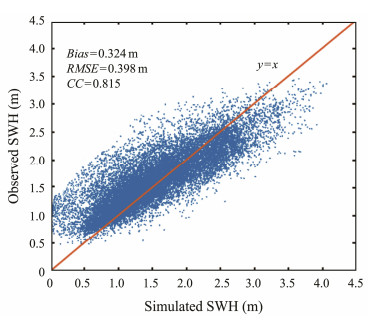
|
Fig. 2 Simulated and observed SWH in SL waters. |
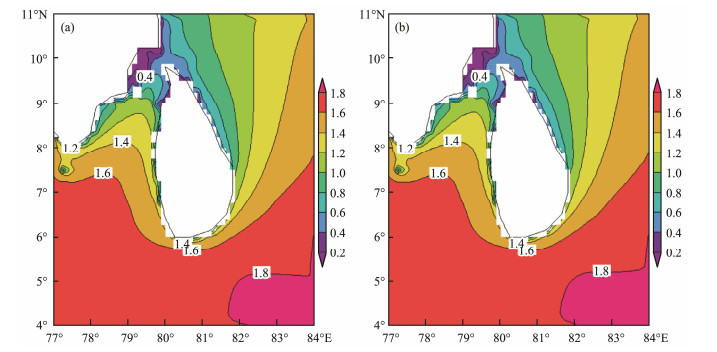
|
Fig. 3 SWH of the south nested boundary at 60˚S and 70˚S. Figs. 3a and 3b show the south nested boundary set at 60˚S and 70˚S, respectively. |
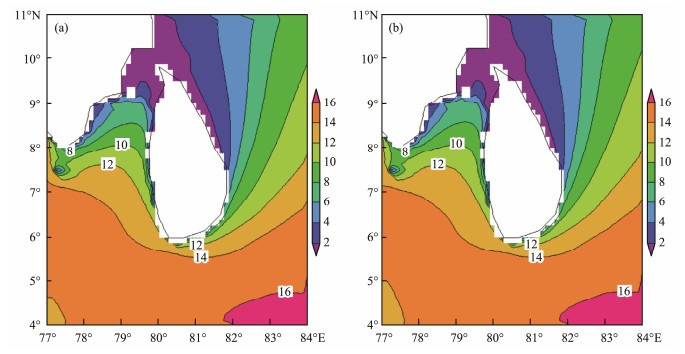
|
Fig. 4 WPD of the south nested boundary at 60˚S and 70˚S. Figs. 4a and 4b show the south nested boundary set at 60˚S and 70˚S, respectively. |
Furthermore, drive WW3 wave model with ERA- interim surface wind to simulate the three-hourly wave field of SL waters from 0000 UTC January 1, 1989 to 2100 UTC on December 31, 2018. WW3 hindcast wave data, the seasonal and spatial of SWH, and available SWH were used to analyze WPD and its stability, energy level frequency, and effective storage of wave energy. The specific method is as follows: the seasonal distribution differences were obtained through the calculation of the average SWH and WPD (frequency of available SWH and rich WPD, coefficient of variation, effective storage of wave energy) at each 0.125˚×0.125˚ grid point in each season. Regional distribution characteristics were analyzed through the calculation of the annual average SWH and WPD (frequency of available SWH and rich WPD, coefficient of variation, effective storage of wave energy) at each 0.125˚×0.125˚ grid point.
3 Seasonal and Regional Distribution of SWH and WPDEvaluating the seasonal and regional distribution characteristics of wave energy in an area is crucial for determining the most suitable position for wave energy harvesting and the optimal season for wave energy development. WPD as a momentous parameter of wave energy assessment was utilized in the research (Kamranzad et al., 2016). In accordance with the computational methods of Iglesias and Carballo (2011), Cornett (2008), and Vosough (2011), the average seasonal WPD at each 0.125˚×0.125˚ grid point in SL waters was calculated on the basis of 30yr hindcast wave data.
In deep water, the calculation formula is as follows:
| ${P_w} = \frac{{\rho {g^2}}}{{64{\rm{ \mathsf{ π} }}}}H_s^2{T_e} = 0.49H_s^2{T_e}.$ | (6) |
In shallow water, the calculation formula is as follows:
| ${P_w} = \frac{{\rho g}}{{16}}H_s^2\sqrt {gd}, $ | (7) |
where Pw is the wave power density (unit: kW m−1), Te represents the energy period (unit: s), d is the water depth (unit: m), ρ is the seawater density (about 1028 kg m−3), Hs is the SWH (unit: m). The SWH can be defined by the following formula:
| ${H_s} = {H_{m0}} = 4{({m_0})^{1/2}}, $ | (8) |
where mn is the spectral moment of order n.
| ${m_n} = \int_0^{2{\rm{ \mathsf{ π} }}} {\int_0^\infty {{f^n}S(f, \theta)} } {\rm{d}}f{\rm{d}}\theta, $ | (9) |
where S(f, θ) signifies the directional spectral density function; f and θ represent frequency and directions, respectively. Energy period can be defined as
| ${T_e} = \frac{{{m_{ - 1}}}}{{{m_0}}}.$ | (10) |
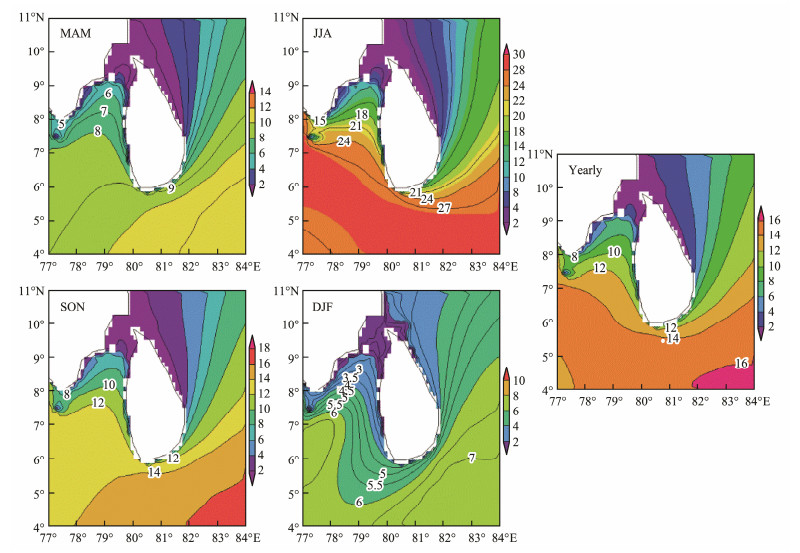
In accordance with 30-year hindcast wave data, seasonal and annual average values of SWH at each 0.125˚× 0.125˚ grid point in SL waters were obtained. The same method was used to obtain seasonal and annual average WPD, as shown in Figs. 5 and 6. Overall, SWH and WPD in SL waters show significant seasonal and spatial differences. The large value areas are mainly concentrated in the south and west of SL. The values of SWH and WPD in the deep waters are larger than those in the shallow waters. The spatial distribution of SWH in each season is basically consistent with that of WPD. Moreover, the overall level of SWH and WPD during JJA and SON is relatively high. In particular, the SWH and WPD during JJA are at the maximum all year round, the large value area of SWH and WPD are mainly concentrated west and south of SL and present a zonal distribution from west to south; their maximum values reach 2.4 m and 28 kW m−1, respectively. In addition, the value of most sea areas are smaller during DJF, the SWH and WPD in the western and southern waters of SL are larger than that in the Gulf of Mannar and the Palk Strait, and the maximum values of SWH and WPD are 1.4 m and 7 kW m−1, respectively. Moreover, the spatial distribution of annual average SWH and WPD is similar to their seasonal spatial distribution, and the maximum values of the SWH and WPD are 1.8 m and 16 kW m−1, respectively. Sabique et al. (2012) once analyzed the propagation of swells in the Indian Ocean and indicated that swells make the largest contribution to WPD during JJA. Zheng and Pan (2014) evaluated global wave energy resources. The seasonal distribution of mixed wave density and swell density indicates that the wave energy resources during JJA are the most abundant. Gunn and Stock-Williams (2012) quantified the wave energy resources in the global ocean in detail, and the results showed that the WPD of SL waters is maintained above 2 kW m−1, and the maximum value of annual average WPD reaches 14 kW m−1. According to the seasonal distribution of SWH and WPD, the seasonal distribution difference of wave energy is closely related to the seasonal characteristics of swell propagation. The analysis results of this study are also consistent with those of its predecessors. In addition, the higher SWH and WPD during JJA are due to the winds of the roaring Westerlies with the huge amount of energy, and the wild wind provides a powerful force for the northward propagation of swells.

|
Fig. 5 Spatial distribution of SWH (unit: m). |
|
Fig. 6 Spatial distribution of WPD (unit: kW m−1). |
In the evaluation of wave energy, the abundance of wave energy resource and exploitable SWH and WPD is closely related to the development and conversion of wave energy. Typically, wave heights between 1.3 and 4.0 m are regarded as the available SWH. Additionally, the energy level frequency is used to characterize the enrichment degree of WPD in this study, in which a WPD greater than 2 kW m−1 is considered exploitable WPD, whereas a WPD greater than 20 kW m−1 is represented by the rich WPD.
On the basis of the 30-year simulated wave data, the frequency value of available SWH at each 0.125˚×0.125˚ grid point was calculated, and then an average frequency value of the exploitable SWH was obtained through regional mean calculation. Through the same method, exploitable and rich WPD were also calculated. Moreover, by traversing the frequency at each grid point (57×57), the maximum value of their frequency was obtained, as shown in Figs. 7a and 7b.

|
Fig. 7 Histogram of availability and energy level frequency. (a) The average availability and energy level frequency. (b) The maximum value of availability and energy level frequency. |
As shown in Fig.5, the average and maximum frequency of rich WPD, available SWH, and WPD present significant differences. During JJA, the value of frequency is the highest all year round, the second is SON, whereas the frequency of DJF and MAM is the lowest. Moreover, a slight difference is observed between the average frequency and the maximum frequency of available WPD, both of which are over 82%. During JJA, the average and maximum frequency of exploitable WPD even reach 93.794% and 100%, and the average frequency of rich WPD reaches 47.535%. The average and maximum frequency of annual available WPD also reach 84.85% and 98.73%; during JJA, indicating that the WPD in the study area is basically above 2 kW m−1. In conclusion, the above analysis shows that SL waters are rich in wave energy resources, and SL waters are suitable for the exploitation of wave energy.
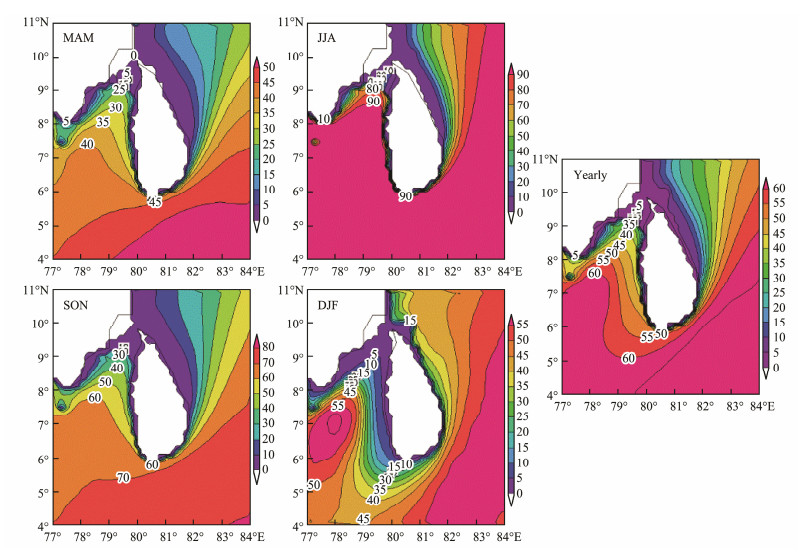
4.2 Seasonal and Annual Distribution Characteristics of Available SWH and Rich WPDTo analyze the seasonal distribution characteristics of available SWH, the occurrence of seasonal and annual available SWH at each 0.125˚×0.125˚ grid point was obtained by using the 30-year WW3 hindcast wave data, as shown in Fig.8. The seasonal variation of available SWH in deep water is greater than that in shallow waters. Large value areas are mainly distributed in the western, southern, and southeastern waters of SL, whereas the occurrence of available SWH in the Gulf of Mannar and the Palk Strait is relatively low. During JJA, the sea area with a frequency of 90% covers almost the entire SL waters. During SON, the high-value area is mainly located in the southern and southeastern parts of SL, and the occurrence of available SWH in most of the waters is above 60%. The occurrence of exploitable SWH in MAM and DJF is relatively low, but the frequency of available SWH in most of the southern waters of SL is also above 50%. Moreover, the annual average available SWH shows evident regional distribution, and the frequencies of exploitable SWH in the southern waters of SL are also above 60%.
|
Fig. 8 Occurrence of seasonal exploitable SWH (unit: %). |
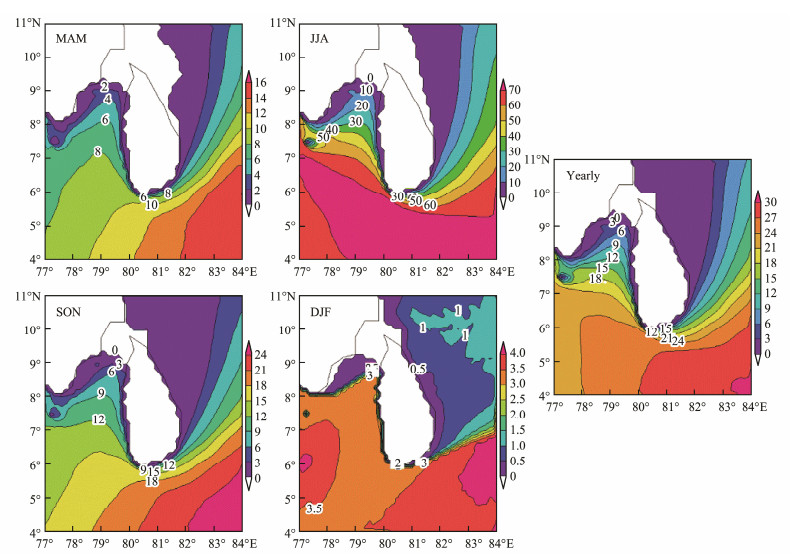
The last section has revealed that WPD in most sea areas are basically above 2 kW m−1, and the spatial distribution of available SWH is not significantly different. Therefore, the analysis of the seasonal distribution characteristics of rich WPD is meaningful. The frequency of rich WPD in JJA and SON is larger than that of MAM and DJF. The frequency of deep waters is larger than that of shallow waters. The occurrence of rich WPD in JJA is relatively large, and the large value areas are located west and south of SL, presenting zonal distribution. During DJF, the frequency of rich WPD is relatively low, and the large value area is mainly concentrated in the western and south-eastern waters of SL, with a maximum frequency of less than 5%. In accordance with the spatial distribution of annual rich WPD, the high-value area is concentrated in the south of SL; moreover, it presents a significant stratification phenomenon, and the maximum value is above 30%. Overall, the advantage of wave energy resources during JJA is evident, and the dominant areas are mainly concentrated in the south and southeast of SL.
5 Quantification of Wave Energy Resources 5.1 Effective Storage of Wave EnergyResource reserves play a crucial part in the quantification of wave energy resources. The total and effective reserves of resources can characterize energy enrichment, but the total storage only represents the overall characteristics of energy resources and has no practical engineering application value; by contrast, the effective storage of resources is related to the conversion and output efficiency of energy. Zheng and Pan (2014) assessed the total and effective reserves of global ocean wind energy. By using their computational formula, the seasonal average effective reserves of wave energy at each 0.125˚×0.125˚ grid point was obtained.
| $E = \bar P \times H \times f, $ | (11) |
where E is the effective storage of wave energy,
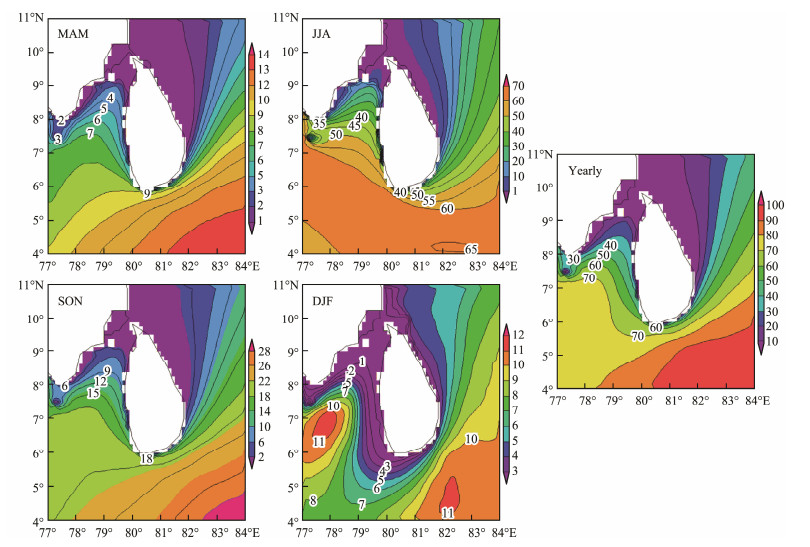
As shown in Fig.10, considerable differences are found in the seasonal distribution of the effective reserves. The high-value areas are mainly distributed in the western, southern, and northeastern waters of SL, and the effective storage of wave energy in the adjacent waters of Palk Strait is relatively low. The variation of the southern sea area of SL is most prominent. The season with the most abundant effective reserves is JJA, whereas the overall level of effective reserves in DJF are the lowest around the year. During JJA, the high-value area is located south of SL, showing an east–west zonal distribution, with a maximum value of 6.5×104 kWh m−1. During DJF, the large-value areas are mainly concentrated in the west and southeast of SL, and the maximum value is 1.1×104 kWh m−1. Moreover, significant differences are observed in the spatial distribution of annual effective reserves, and the effective energy storage in the southeastern waters of SL is the largest, with a maximum of 1×105 kWh m−1. In conclusion, the seasonal distribution of effective reserves in SL waters is consistent with the previous analysis; moreover, JJA is the dominant season of wave energy resources, and the southeastern waters of SL are the dominant area.
|
Fig. 9 Occurrence of seasonal rich WPD (unit: %). |
|
Fig. 10 Effective storage of wave energy resources (unit: 1×103 kWh m−1). |
The contributions of the waves with different SWH and energy period to total power must be explored. In accordance with the values of SWH and energy period, the contribution of waves to wave power under different wave conditions at each season was calculated, as shown in Fig.11. The wave energy contribution of JJA is dominant. Moreover, the contribution rate of wave energy accounts for 46.56% in JJA. The largest contribution to wave power is provided by wave conditions with an SWH of 2–3 m and an energy period of 7–11 s. The typical wave power of such waves is on the order of 20 kW m−1. Therefore, using wave energy converters designed for these wave parameters in SL waters is reasonable. Although much higher levels of instantaneous wave power flux may appear at the study area, such waves are infrequent. The wave power flux exceeds 100 kW m−1 on few occasions.
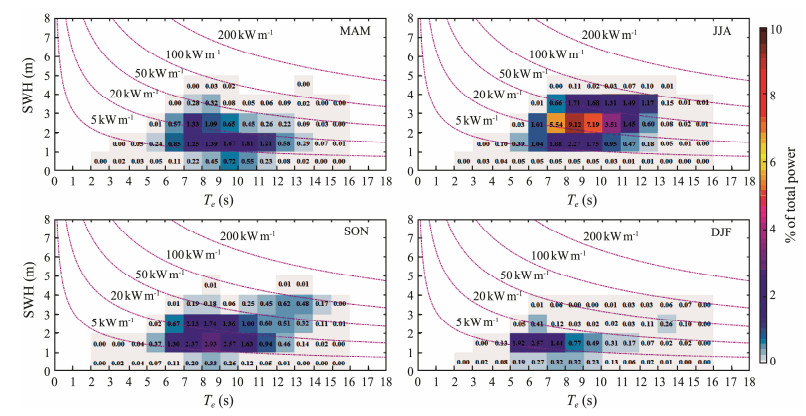
|
Fig. 11 Bivariate distributions of occurrences corresponding to the sea states defined by SWH and energy period. The color scale is used to represent the contribution of the sea state to the total incident energy as a percentage. The wave power isolines are indicated by the purple dotted lines. |
The stability of energy resources is concerned with the collection and conversion efficiency of the equipment, and it affects the service life of the device. In this study, the variation coefficient (Cv) of WPD is used to characterize the stability of energy resources. The smaller the Cv, the higher the stability of wave energy resources. To analyze the regional and seasonal differences of wave energy stability in SL waters, the average Cv of WPD at each 0.125˚×0.125˚ grid point was obtained on the basis of the quarterly and yearly WPD. The calculation formulas are as follows:
| ${C_v} = \frac{S}{{\bar x}}, $ | (12) |
| $S = \sqrt {\frac{{\sum\nolimits_{i = 1}^n {x_i^2 - (\sum\nolimits_{i = 1}^n {x_i^2})} /n}}{{n - 1}}}, $ | (13) |
where Cv is the coefficient of variation, x is the mean value of WPD, S is the standard deviation, and n represents the total number of samples.
As shown in Fig.12, Cv presents significant spatial and seasonal differences. Cv of most sea areas is less than 1.0, and the stability of wave energy resources is relatively high. The spatial distribution of Cv in MAM is similar to that in SON, and Cv of almost the entire study area stays below 1.0. The sea areas with a Cv of 0.5 appear in JJA and DJF. Especially during JJA, Cv in the western and southern waters of SL is no more than 0.5, and the stability of wave energy resources is higher than that of other months. During JJA, the southern hemisphere experiences winter; furthermore, the wind speed of the southern Indian Ocean westerlies is strongest throughout the year and more conducive to the northward propagation of swells. That is, southern Indian Ocean swells have a greater effect on SL waters in JJA that in other months. In addition, according to the spatial distribution of the annual mean Cv, Cv in most sea areas is less than 1.0; thus, the wave energy resources in the entire study area are relatively stable.

|
Fig. 12 Seasonal distribution characteristics of the coefficient of variation. |
In previous analyses, regardless of SWH, WPD, and the effective storage of wave energy, the wave energy resources in JJA are superior to that of other months. Additionally, Cv of WPD in JJA is smaller and far more favorable for the development of wave energy resources and the location selection of wave energy conversion equipment.
7 ConclusionsOn the basis of 30-year hindcast wave data, the SWH and WPD, the occurrence of exploitable SWH and rich WPD, the effective storage of wave energy, and the contribution and stability of wave energy were analyzed. The significant seasonal and regional differences of wave energy resources in SL waters were also found. The important results are as follows:
1) The spatial distribution of SWH and WPD have significant seasonal and regional characteristics in SL waters. An optimistic SWH and WPD is found in JJA, with maximum values of 2.4 m and 28 kW m−1, respectively. From the perspective of the occurrence of exploitable SWH and rich WPD, their seasonal spatial distribution also exhibits the characteristics mentioned above, and the overall level of JJA is high. In accordance with their spatial distribution, the large-value area is concentrated in the western, southern, and southeastern of SL.
2) Through the calculation of the effective storage of wave energy, the maximum effective storage is found during JJA. The energy contribution of JJA is dominant, and the largest contribution to wave power is provided by wave conditions with an SWH of 2–3 m and an energy period of 7–11 s. In accordance with the spatial distribution of the effective storage of annual wave energy, the dominant region of wave energy is mainly concentrated in the western, southern, and southeastern waters of SL.
3) On the basis of the variable coefficients of WPD, the stability of wave energy resources in the study area was analyzed. The stability of wave energy in JJA is higher than that of other months, and Cv in most sea areas remains at approximately 0.5. According to the spatial distribution of the annual mean Cv, Cv in most sea areas is less than 1.0.
On these bases, the dominant regions are located in the western, southern, and southeastern waters of SL, and the optimal season with the largest contribution to wave power is JJA. The dominant season and regions for energy supply must be focused on for the coastal zone management and development of crucial regions.
AcknowledgementsWe sincerely thank the European Center for Medium-Range Weather Forecasts for providing ERA-Interim reanalysis dataset, and appreciate the numerical simulation model (WW3) provided by WAM. The work was supported by the Key Technology Research and Development Program of Shandong (Nos. 2019GHY112072, 2019GHY112051), and the State Key Laboratory of Precision Measuring Technology and Instruments (No. pilab1906). We also got a grant from the Key Research and Development Program of Tianjin (Nos. 18YFZCSF00620, 18YFYSZC001 20).
Aarnes, O. J., Abdalla, S. and Bidlot, J. R., 2015. Marine wind and wave height trends at different ERA-Interim forecast ranges. Journal of Climate, 28(2): 819-837. DOI:10.1175/JCLI-D-14-00470.1 (  0) 0) |
Aboobacker, V. M., Samiksha, S. V. and Vethamony, P., 2012. Propagation of Atlantic Ocean swells in the North Indian Ocean: A case study. Natural Hazards and Earth System Sciences, 12(12): 3605-3615. DOI:10.5194/nhess-12-3605-2012 (  0) 0) |
Bhowmick, S. A., Kumar, R., Chaudhuri, S. and Sarkar, A., 2011. Swell propagation over Indian Ocean region. International journal of ocean and climate systems, 2(2): 87-99. DOI:10.1260/1759-3131.2.2.87 (  0) 0) |
Bento, A. R., Martinho, P. and Soares, C. G., 2015. Numerical modelling of the wave energy in Galway Bay. Renewable Energy, 78: 457-466. DOI:10.1016/j.renene.2015.01.024 (  0) 0) |
Chen, G., Chapron, B., Ezraty, R. and Vandemark, D., 2002. A global view of swell and wind sea climate in the ocean by satellite altimeter and scatterometer. Journal of Atmospheric and Oceanic Technology, 19(11): 1849-1859. DOI:10.1175/1520-0426(2002)019<1849:AGVOSA>2.0.CO;2 (  0) 0) |
Cornett, A. M., 2008. A global wave energy resource assessment. Proceedings of the Eighteenth International Offshore and Polar Engineering Conference. Ontario, Canada, 318-326.
(  0) 0) |
Gopalakrishnan, G., Hoteit, I. and Cornuelle, B. D., 2019. Comparison of 4DVAR and EnKF state estimates and forecasts in the Gulf of Mexico. Quarterly Journal of the Royal Meteorological Society, 145(721): 1354-1376. DOI:10.1002/qj.3493 (  0) 0) |
Gunn, K. and Stock, -Williams C., 2012. Quantifying the global wave power resource. Renewable Energy, 44: 296-304. DOI:10.1016/j.renene.2012.01.101 (  0) 0) |
Idris, N., Deng, X., Din, A. H. M. and Idris, N. H., 2017. CAW-RES: A waveform retracking fuzzy expert system for optimizing coastal sea levels from Jason-1 and Jason-2 satellite altimetry data. Remote Sensing, 9(6): 1-22. (  0) 0) |
Iglesias, G. and Carballo, R., 2011. Choosing the site for the first wave farm in a region: A case study in the Galician south-west (Spain). Energy, 36(9): 5525-5531. DOI:10.1016/j.energy.2011.07.022 (  0) 0) |
Kamranzad, B., Etemad-Shahidi, A. and Chegini, V., 2016. Sustainability of wave energy resources in southern Caspian Sea. Energy, 97: 549-559. DOI:10.1016/j.energy.2015.11.063 (  0) 0) |
Langodan, S., Viswanadhapalli, Y., Dasari, H. P., Knio, O. and Hoteit, I., 2016. A high-resolution assessment of wind and wave energy potentials in the Red Sea. Applied Energy, 181: 244-255. DOI:10.1016/j.apenergy.2016.08.076 (  0) 0) |
Lavidas, G. and Venugopal, V., 2018. Application of numerical wave models at European coastlines: A review. Renewable & Sustainable Energy Reviews, 92: 489-500. (  0) 0) |
Liu, L., Yao, Y., Kong, J. and Shan, L. L., 2018. Plasmaspheric electron content inferred from residuals between GNSS- derived and TOPEX/JASON vertical TEC data. Remote Sensing, 10(4): 1-20. (  0) 0) |
Marcos, R., Gonzalez-Reviriego, N., Torralba, V., Soret, A. and Doblas, -Reyes F., 2019. Characterization of the near surface wind speed distribution at global scale: ERA-Interim reanalysis and ECMWF seasonal forecasting system 4. Climate Dynamics, 52(5-6): 3307-3319. DOI:10.1007/s00382-018-4338-5 (  0) 0) |
Sabique, L., Annapurnaiah, K., Nair, T. M. B. and Srinivas, K., 2012. Contribution of southern Indian Ocean swells on the wave heights in the northern Indian Ocean – A modeling study. Ocean Engineering, 43: 113-120. DOI:10.1016/j.oceaneng.2011.12.024 (  0) 0) |
Samiksha, S. V., Vethamony, P., Aboobacker, V. M. and Rashmi, R., 2012. Propagation of Atlantic Ocean swells in the north Indian Ocean: A case study. Natural Hazards and Earth System Sciences, 12(12): 3605-3615. DOI:10.5194/nhess-12-3605-2012 (  0) 0) |
Semedo, A., Suselj, K., Rutgersson, A. and Sterl, A., 2011. A global view on the wind sea and swell climate and variability from ERA-40. Journal of Climate, 24(5): 1461-1479. DOI:10.1175/2010JCLI3718.1 (  0) 0) |
Soares, C. G., Bento, A. R., Goncalves, M., Silva, D. and Martinho, P., 2014. Numerical evaluation of the wave energy resource along the Atlantic European coast. Computers & Geosciences, 71: 37-49. (  0) 0) |
Taszarek, M., Brooks, H. E. and Czernecki, B., 2018. Climatological aspects of convective parameters over Europe: A comparison of ERA-Interim and sounding data. Journal of Climate, 31(11): 4281-4308. DOI:10.1175/JCLI-D-17-0596.1 (  0) 0) |
Tolman, H. L., 1991. A third-generation model for wind waves on slowly varying, unsteady, and inhomogeneous depths and currents. Journal of Physical Oceanography, 21(6): 782-797. DOI:10.1175/1520-0485(1991)021<0782:ATGMFW>2.0.CO;2 (  0) 0) |
Uihlein, A. and Magagna, D., 2016. Wave and tidal current energy – A review of the current state of research beyond technology. Renewable & Sustainable Energy Reviews, 58: 1070-1081. (  0) 0) |
Ulazia, A., Penalba, M., Ibarra-Berastegi, G. and Saenz, J., 2017. Wave energy trends over the Bay of Biscay and the consequences for wave energy converters. Energy, 141: 624-634. DOI:10.1016/j.energy.2017.09.099 (  0) 0) |
Vosough, A., 2011. Wave power. International Journal Of Engineering Science, 2(7): 60-63. (  0) 0) |
Wang, Z. F., Duan, C. L. and Dong, S., 2018. Long-term wind and wave energy resource assessment in the South China Sea based on 30-year hindcast data. Ocean Engineering, 163: 58-75. DOI:10.1016/j.oceaneng.2018.05.070 (  0) 0) |
Zhang, Z., Zheng, C. W. and Wang, M. X., 2018. Offshore wind energy and energy of the '21st Century Maritime Silk Road'. Ocean Development and Management, 4: 63-66 (in Chinese with English abstract). (  0) 0) |
Zheng, C. W. and Li, C. Y., 2015. Variation of the wave energy and significant wave height in the China Sea and adjacent waters. Renewable & Sustainable Energy Reviews, 43: 381-387. (  0) 0) |
Zheng, C. W. and Li, C. Y., 2017. Propagation characteristic and intraseasonal oscillation of the swell energy of the Indian Ocean. Applied Energy, 197: 342-353. DOI:10.1016/j.apenergy.2017.04.052 (  0) 0) |
Zheng, C. W. and Pan, J., 2014. Assessment of the global ocean wind energy resource. Renewable & Sustainable Energy Reviews, 33: 382-391. (  0) 0) |
Zheng, C. W., Li, C. Y. and Chen, X., 2016. Numerical forecasting experiment of the wave energy resource in the China Sea. Advances in Meteorology, 2016: 1-12. (  0) 0) |
Zheng, C. W., Pan, J. and Li, J. X., 2013a. Assessing the China sea wind energy and wave energy resources from 1988 to 2009. Ocean Energy, 65: 39-48. DOI:10.1016/j.oceaneng.2013.03.006 (  0) 0) |
Zheng, C. W., Shao, L. T. and Shi, W. L., 2014. An assessment of global ocean wave energy resources over the last 45 a. Acta Oceanologica Sinica, 33(1): 92-101. DOI:10.1007/s13131-014-0418-5 (  0) 0) |
Zheng, C. W., Zhou, L. and Huang, C. F., 2013b. The long-term trend of the sea surface wind speed and the wave height (wind wave, swell, mixed wave) in global ocean during the last 44 a. Acta Oceanologica Sinica, 32(10): 3-6. (  0) 0) |
 2021, Vol. 20
2021, Vol. 20


