Artificial reef is a submerged structure that is deliberately constructed and deployed on the seabed. It can change the flow pattern of the bottom water layer in the sea area, provide habitat for marine life to grow and reproduce, and play important roles in restoring the marine ecological environments and conserving marine fishery resources (Kim et al., 2016). When an artificial reef is deployed on the seabed, it can change the seafloor conditions. These changes may exacerbate scouring or even cause artificial reefs to sink, leading to overturning or the burial of artificial reef and ultimately affecting the ecological restoration function of artificial reefs.
In ocean engineering, the movement of sediment around the marine structure and the nearby seafloor due to the action of waves and currents is known as the local scour phenomenon (Lin and Lin, 2020). The erosion of the seabed around an artificial reef is a problem associated with the dynamic coupling of fluid, the reef, and the sediment in the seabed. Erosion is affected by various environmental factors such as flow, topography, and sediment quality. From the perspective of fluid dynamics, the scour of artificial reefs involves the unsteady motion of vortex separation. If the seabed shear force generated by the hydrodynamic force is greater than the critical stress of the sediment, the bed scour will occur, and the bed boundary will dynamically change.
For some types of subsea structures, such as submarine pipelines, the local scour problem has been widely studied (Yu et al., 2016). Scouring occurs when the local water flow is too strong, and the sediment flux brought by the water flow is smaller than the local scour outward flux (Chatanantavet and Lamb, 2014). The main reason for the formation of seabed scour is the destruction of the original underwater flow field following the placement of submarine structures (Singh et al., 2016; Wang et al., 2019), which results in the acceleration of local water flow and strong seabed shear (Sumer and Fredsøe, 2002). Simultaneously, the emergence of submarine structures changes the direction of flow, generating circumfluence and local large-scale vortexes (Castro and Robins, 1977; Bauri and Sarkar, 2016), which also accelerate seabed scouring (Dey and Barbhuiya, 2005; Keshavarzi et al., 2018; Yang et al., 2020). Therefore, the submarine structure is an important factor affecting the local scour.
The scientific problems related with the burial and scour of the artificial reef are far more complex and difficult due to their porosity and spatial structure, compared with those traditional ones of coastal and offshore marine engineering. The local scour of sediments around the artificial reefs has been identified as a key factor leading to structural failure in coastal and offshore engineering. Researchers in Singapore found that the difference in seabed sediment is the main factor affecting a tendency of a reef to scour effect. The physical model experiments and numerical simulations were performed to study the scour phenomenon around the reef, and it was found that the scour was related to the particle size of the seabed sediment and incoming water velocity (Nguyen et al., 2016; Bao and Liu, 2017). It was also found that the local scour depth of the artificial reef increases with the increase of the flow velocity under the condition of silt seabed (Ding et al., 2019). Yun and Kim (2018) found that the installation of geogrid or geogridbamboo mat reinforcements on a soft seabed floor contributes to a reduction in settlement and scour of the artificial reef. The research on the scouring of the artificial reef has become an increasingly hot topic; however, the previous studies did not systematically consider the problem of the local scour of artificial reefs under different structural parameters.
The purpose of this study is: 1) to explore the influence of various factors on the scour of an artificial reef by conducting a mechanistic study; 2) to optimize the geometry of the reef and identify a natural anti-scour design; 3) to investigate the evolving relationship of scour depth with time and determine the final time required to reach scour balance; and 4) to determine the main controlling factors that influence reef scour and establish an empirical formula for the scour depth in relation to various factors.
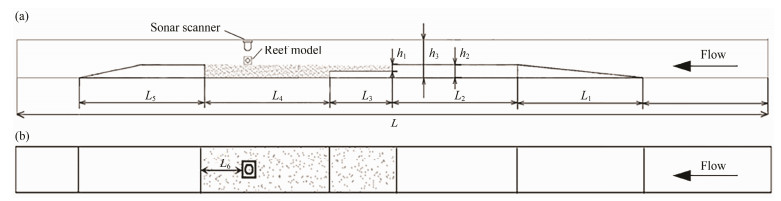
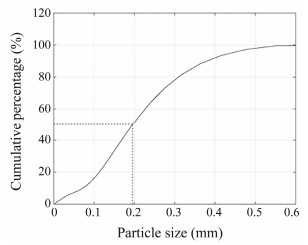
2 Test Setup and Test Conditions 2.1 Test SetupIn the present study, physical model experiments are carried out in the flume tank in the State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology. The flume tank is 22 m in length, 0.45 m in width, and 0.6 m in height. To ensure the smooth progress of the experiment and the development of the uniform incoming flow, a concrete terrain is built at the bottom of the flume tank with a total length of 9 m. The front edge of the terrain is located at 2 m from the right end of the flume tank where water flow comes from. The topography mainly includes: 1) a wedge-shaped drainage section with a length L1 = 2 m; 2) a parallel drainage section with a length L2 = 2 m; 3) a sand supplement section with a length L3 = 1 m and a thickness h1 = 0.1 m; 4) a test sand section with a length L4 = 2 m and a thickness h2 = 0.2 m; 5) a tail section and its length L5 = 2 m. The total length of the entire test section is L = 12 m, and the height between the water surface and the bottom of the flume tank is h3 = 0.5 m. The depth of the water is h = h3−h2 = 0.3 m. The side view of the flume tank is shown in Fig.1. The sand used in the experiments has a median diameter of d50 = 0.195 mm. The grading curve of the sediment is plotted in Fig.2.
|
Fig. 1 Schematic view of the flume tank. (a), side view; (b), vertical view. |
|
Fig. 2 Sediment grading curve, d50 = 0.195 mm. |
The model of the artificial reefs is placed at 0.7 m away from the back end of the test sand section. There are two main measurement instruments. One is a 50-mm 3D profiler, i.e., a sonar terrain scanning system which is placed directly above the artificial reef. The other one is an Acoustic Doppler Velocimetry (ADV) to measure the velocity. The sonar scanner is placed above the origin of the coordinate, i.e., right above the reef model, for terrain scanning and data collection. A uniform flow is generated from the right end of the flume tank.
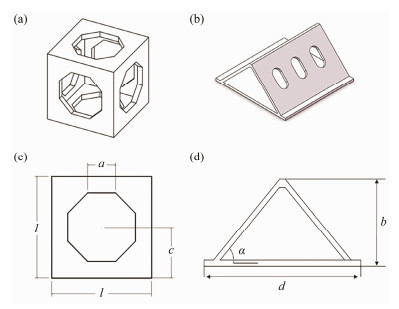
2.2 Test ModelsAs shown in Fig.3, the model experiments of two types of artificial reefs, i.e., the cubic reef and the triangular reef, are carried out. Cubic concrete artificial reefs (2.0 m × 2.0 m × 2.0 m) and triangular concrete artificial reefs (3.346 m × 3.3 m × 1.514 m) are chosen as the prototypes for the experimental design. Due to the limitation of the size of the flume tank, the scale ratios of two types of models are set as 1:20 and 1:30, respectively. The specifications of the prototypes and models are presented in Table 1. The models are made of steel because of its high density and the ability to withstand the impacts of the water flow.
|
Fig. 3 Two types of artificial reefs. (a), the cubic artificial reef; (b), the triangular artificial reef; (c), projection of cubic reef with side length of cubic reef l, opening length of the cubic reef a, opening height of cubic reef c; (d), projection of triangular reef with side length of triangular reef d, height of triangular reef b, and bottom angle α. |
|
|
Table 1 Main dimensions and parameters of two types of artificial reefs |
The cubic artificial reef is composed of six square-shaped boards as its surfaces. The side length is l. There is an octagon-shaped opening hole, with a side length a on each surface of it. To measure the size of the opening holes, a nondimensional parameter, i.e., the open-area ratio γ, is adopted, which is defined as the ratio between the area of the opening hole and the total area of the front surface. Since the opening hole is an octagon in the present study, the open-area ratio can be calculated as:
| $ \gamma = (2 + 2\sqrt 2){a^2}/{l^2}. $ | (1) |
Another parameter involving opening holes is its height on the upstream surface, which refers to the height of the center of the hole measured from the bottom edge of the front surface. It is denoted by c in Fig.3c.
For the triangular reefs, the important parameter is the bottom angle α, which is the angle between the upstream lateral surface and the bottom surface (see Fig.3d).
2.3 Experiment Arrangement and Test ConditionsIn the present study, the effect of the open-area ratios, the open-hole heights of the cubic reefs, and the bottom angles of the triangular reefs on the local scour of the models are investigated. As a phenomenon of sediment erosion, the local scour is divided into two categories, i.e., the so-called clear water scour and lived bed scour. As the current velocity is not so great, the shear stress of the seabed remains at a low level. The seabed sand maintains stationary and the seawater looks 'clean', namely 'clear water scour'. The shear stress increases with the increase of the current velocity. Once it exceeds the critical stress, the sand in the seabed will fluctuate around its balanced position. The seabed looks 'alive', referred to as 'lived bed scour' (Chiew, 1984; Yang et al., 2019). Here, the critical velocity of the current, i.e., the velocity causing the critical shear stress of seabed, should be considered in the scour experiments (Liu et al., 2018). It is determined mainly by the physical properties of seabed sand. Here it only refers to the calculation result of critical velocity from the appendix, namely Ucr = 0.274 m s−1.
The prototypes of the artificial reefs are laid in the Laoshan Bay of the Yellow Sea in China, where the flow velocity is about 1.0–1.5 m s−1. According to the Froude's similarity law, the velocity scale ratio λv is the square root of the scale ratio λL, i.e., λv =
The experiments are arranged into four groups. As shown in Table 2, each group has four runs. In the first group (run Nos. 1–4), the cubic reef model with an open-area ratio γ = 0.38 and opening height c = 0.05 m is chosen to examine the effect of flow velocity on the local scour. The flow speed is set to 0.20, 0.22, 0.24 and 0.26 m s−1, respectively.
|
|
Table 2 Experiment runs and test conditions |
In the next three groups, the effects of the shape factor of the artificial reefs on the local scour are investigated. The flow speed is fixed at U = 0.22 m s−1, which is chosen to minimize the influences of the sand movement in the seabed on test results and to amplify the impact of the shape of the structures on the scouring.
In the second group (run Nos. 5–8), the effect of the open-area ratios on the local scour is studied. Four cubic reef models with the same opening height c = 0.05 m and various open-area ratios of front surface are tested. The open-area ratios are 0, 0.12, 0.25, and 0.49, respectively. Together with the results of run No. 2 in the previous group, comparisons among five models with different open-area ratios can be made to examine the effect of open-area ratios on the local scour. In the third group (run Nos. 9–12), the effect of the open-hole heights is considered. Four cubic reef models with the same open-area ratio γ = 0.25 and various open-hole heights are tested. Together with the results of run No. 7 in the second group, the effect of open-hole heights is explored by comparing the test results of five types of models. In the last group (run Nos. 13–16), four triangular reef models with various bottom angles are tested to find out how the bottom angles of triangular reefs affect the local scour.
Before doing the scour tests, the velocity at the location where the model is to be placed, are measured firstly. The distribution of velocity over the water depth is plotted in Fig.4 with the fitting function as follows:
| $ {U_{(z)}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{{U_f}}}{{5.433}}\ln (4.44 \times {{10}^3}z)\ \ \ \ ({U_{(z)}} < 0.99{U_f})} \\ {{U_f}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (0.99{U_f} < {U_{(z)}} \leqslant {U_f})} \end{array}} \right.. $ | (2) |

|
Fig. 4 Distribution of velocity over water depth. |
Here, U(z) represents the velocity in water depth z, and Uf is the inflow velocity.
It can be obtained from the results that the greater the current velocity, the smaller the boundary layer thickness. The boundary layer thickness is about 0.05 m at the velocity of 0.20 m s−1 in this study (Soulsby, 1997).
The general procedure for each run is as follows: a) to level the model seabed; b) to fill the flume tank with water, taking caution to avoid disturbing the bed surface during the filling process; c) to scan the initial seabed profile with the 3D sonar scanner to collect the data of initial bed height; d) to install the reef model in the test section and initiate video capture; e) to start the test and run it until reaching the equilibrium stage for local scour; f) to stop the flow and video, take the model out of the tank, and scan the final scour profile with the 3D sonar scanner to obtain the final bed height; g) to end this set of experiments, and drain the water out of the tank.
3 Methods of Analyses 3.1 Determination of Scouring TimeIn order to find the 'equilibrium criteria' of scour, a number of expressions to represent the time evolution of the scour can be found in the literature (Melville and Sutherland, 1988; Baykal et al., 2015; Petersen et al., 2015; Tavouktsoglou et al., 2017). The development of the scour depth at the most-front upstream point of a vertical circular or a rectangular pile can be obtained by an exponential function (Sumer et al., 1992). Through this formula, the scouring depth at any time can be obtained, and scour depth and time can be obtained by fitting the scouring data at different times. But this formula can only be applied to the cylindrical scouring without holes.
Since two types of reef models used in the present study have their own unique designs compared with the cylinder and the caisson. They both have the hollow structure on the frontal surface, and the inclined frontal surface of the triangular artificial reef also changes the angle of the front stream, which can cause the scour process to be slow and complex. As the result, the cylindrical scouring formula proposed by predecessors might not be applicable to predict the scouring equilibrium time. Therefore, before the formal tests, a preliminary experiment is performed to determine the scouring time.
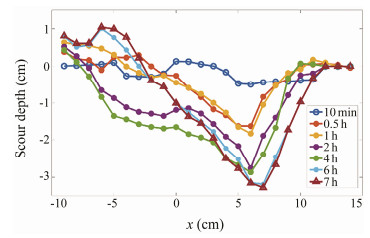
In the preliminary experiment, the velocity is set to 0.22 m s−1, and the cubic artificial reef used in run No. 2 is selected as the test model. The scour depth is detected along the line coinciding with the sharp corner on the left side of the model. This line is referred to as the x-axis, with the origin located at the middle point of the model sideline. The measurement is from the point that is 14 cm in front of the model to the point which is 9 cm behind the model, with the total length of 23 cm. The change in the height of the seabed is detected at every 1 cm along the x-axis and there is a total of 23 monitoring points. The measurement is made at 1/6 h, 0.5 h, 1 h, 2 h, 4 h, 6 h, and 7 h after scouring begins.
The results of the preliminary test are presented by seven curves of scouring depth at each measuring time, as shown in Fig.5. It can be observed that scouring developed rapidly in the early stage of the test and then the scouring rate gradually slows down. Finally, after 6–7 h, the change of seabed is not so significant. It means that the scouring equilibrium has been reached in this experiment. Therefore, the time for the formal experiments is set to 7 h.
|
Fig. 5 The distribution of bed levels along the flow direction at each measuring time. |
As mentioned in the previous section, the sonar scanner is fixed right above the reef model. It scans the points below the probe within a radius of 0.1 m to 0.5 m. The collection area is about 0.754 m2, the data points collected each time are about 60000 and the collection density is 80000 dots m−2. The 'height' here is referred to the vertical distance of each point to the bed measured from the horizontal plane where the sonar scanner is located. Once the height of each point is collected, they are input into the software MeshLab for preprocessing. By means of MeshLab, the data with obvious errors and deviations are deleted. To restore the data at these points, the method of interpolation by 'grid data' is adopted later. These data are input into the software Excel for secondary screening. Then a full topography map is drawn by the software MATLAB. This map is compared with the actual terrain in the flume tank to make sure that they are basically the same.
The data collection and processing discussed above are made twice for each run of the test, i.e., before and after the test. For each test, the initial height of the seabed surface is firstly measured after the sand bed is leveled and water is filled into the flume tank. Then, the preprocessed data from MeshLab is input into Excel. Instead of depicting a topography map, the average value of the total data is made within a rectangular area of 50 cm × 30 cm around the model to obtain the average initial bed height denoted by sbed. When each scouring test is finished, the sonar scanner is operated once again to collect the 'height' of the sand bed below, which is designated as the depth z. The difference between these two heights, i.e., s = sbed−z, indicates the results of scouring. The value of s > 0 implies that the sediment has been accumulated while the case of s < 0 means that scouring has occurred.
An example is presented in Fig.6, which is the result of a scouring test without a model, running for 5 h with the velocity of 0.22 m s−1. The initial terrain is scanned with the sonar as shown in Fig.6a. The data are imported into MeshLab for simple filtering as shown in Fig.6b. The processed data are then input into MATLAB to draw a point cloud image as shown in Fig.6c, from which the impact range of scour around the reef model and the specific location and size of subsidence and siltation can be observed. The color bar indicates the scouring (negative values) or accumulation (positive value) depth. It can be observed that the topography map (Fig.6d) is clearly depicted and comparable to the picture (Fig.6c) taken after the test.
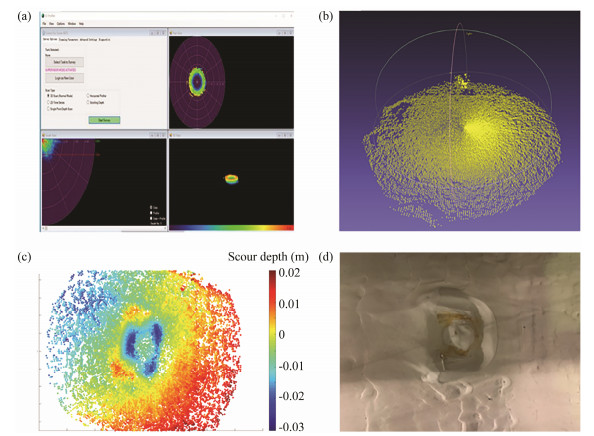
|
Fig. 6 Topographic data collection and processing steps after running test at a current speed of 0.22 m s−1 for 5 h. (a), topographic data collected by sonar scanner; (b), preprocessing using MeshLab; (c), actual topographic point map imported into MATLAB; (d), the picture taken by camera. |
The advantage of the sonar scanner used in this study is that the whole scanning process is fully automatic. It can reduce the points missed by scanningwith laser rangefinder, an instrument commonly used in the previous experiments.
4 Results and Discussion 4.1 Time Scale of the Scour DepthThe time scale of the scour describes how the scour depth varies with time. Some important physical quantities, such as the equilibrium depth of scour, time to reach equilibrium, scouring rate, and type of scour can be determined by analyzing the curve of scouring depth over time. It helps to make a comprehensive study of the erosion problem. In order to determine whether the time scale of scour changed, run Nos. 2, 7, 8 and 14 with different openings and types are chosen as examples. As shown in Table 3, new four test runs (run Nos. 17, 18, 19, and 20) are designed to explore the relationship between the scouring process and time of the four models mentioned above every 0.167 h, 0.5 h, 1 h, 2 h, 4 h, 5 h, 6 h, and 7 h. The results are presented in Fig.7, from which it can be observed that the local scour around the reef model is developed through three stages.
|
|
Table 3 Results derived from the development history of four tests |
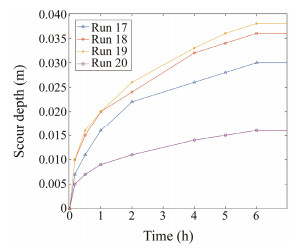
|
Fig. 7 Development of scour depth at the two upstream corners of the reef. |
In the initial stage, which occurs at about the first half an hour, the scour develops rapidly, and the scour depth increases quickly, reaching 1/3, even 1/2 of the final scour depth. In this stage, the size and number of vortices are small, but the scouring ability is the strongest. With the scouring pit getting deeper, the current speed at its bottom decreases and the scouring capacity weakens.
Then, it enters the second stage, the development stage, during which the depth of the scouring pit continues to increase, but the increasing rate (∆ht/∆t) slows down. The scouring process shows a close to stable trend, while the effect of the vertical vortex flow above the scouring pit is gradually weakened
At the final stage, the scour depth no longer changes significantly with time. It reaches a balanced state, and the scour depth approaches the maximum value asymptotically. In this stage, the scour is mainly caused by the pulsating flow and develops very slowly. The shape of scouring pit remains basically unchanged, and the scouring gradually stabilizes. At this time, there is no obvious change in the whole scour topography, and the equilibrium of local scour is finally achieved. As shown in Fig.7, all test runs have reached equilibrium at approximately 7 h. The above observation is in agreement with the conclusion made in the previous work (Gao et al., 1998).
Calculated by the scouring formula, the scouring of a cylinder with similar size usually takes more than 24 h to reach the scouring equilibrium (Pandey et al., 2017). But artificial reefs are randomly placed on the surface of the seabed, which is different from some structures designed to be fixed on the seabed. When a scouring pit appears at the bottom, the artificial reef will sink continuously into the sand, together with the expansion of the scouring pit. As the worst result, it might be buried by the sand. During this process, the contact area facing the incoming flow will become smaller and smaller as it sinks into the sand, which slows down the effect of scour. Therefore, the scour around artificial reefs will reach balance faster than around other fixed structures.
4.2 Topographic Features of the Local Scour Around the Artificial ReefThe whole procedure of scour around the reef model, including the change in the shape of scouring pit and the development of its scope, is observed and recorded by video camera during the tests. The results are summarized as follows.
Right after the scour test starts, the upstream current remains clear. The flow pattern changes significantly after the current hits the reef model, which causes local scour around the model. The scouring pits first appear at the two upstream corners. As time passes, these two scouring pits grow deeper and extend toward the central part of the model's front surface. Then the scour occurs around two downstream corners, as well as along the two sides of the model. At the same time, the downstream water behind the model becomes turbid, and the rolled sands are suspended in the water, then washed downwards to cause sedimentation. The sediment deposition in downstream is mainly due to the transport of bed-borne sediments. The volume of sediment dunes deposited behind the model appears smaller than that of sands scoured away from the scouring pits, which implies that a part of suspended sediment is transported by the current further downstream.
The results of four test runs in Group Ⅱ are selected as examples to explore the final erosion pattern. The flow velocity is set to 0.22 m s−1 in these tests. Fig.8 shows the topographic map of the scour results after 7 h. The set velocity (0.22 m s−1) is less than the critical velocity (0.274 m s−1). Therefore, the scour is only generated around the reef, and the entire bed surface is not excessively deformed. Since the incoming current is uniform and stable, the streamline at each point on the front face of the reef is the same. The resulting flow field changes are also similar. Eventually the symmetrical scouring pit is formed along the center line of the reef. The scouring areas appear mainly in front of the model, with a width varying from 10 cm to 15 cm. Moreover, as it is scoured under the 'clear water' state, the sediment scoured from the pit is transported downstream and then is rapidly buried at the rear of the model to form sand dunes, reaching a height of 4 cm in some cases. The maximum scouring depth appears at the two front corners of the model facing the current. Compared with the scour depth on the upstream surface, the scour depth on both sides of the reef is shallower, which is less than 1cm, and no sediment accumulation occurs on either side of the model body.
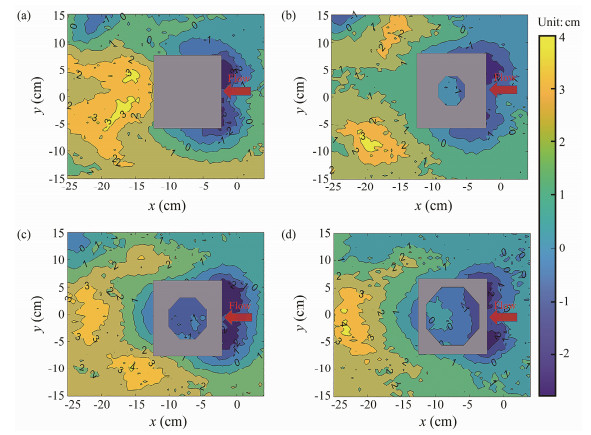
|
Fig. 8 Contours of the final bed level after scouring for 6 h at different open-area ratios. (a), run 5 with γ = 0; (b), run 6 with γ = 0.12; (c), run 7 with γ = 0.25; (d), run 8 with γ = 0.49. |
Table 4 shows the variation in scour depth for various current speeds. The scour depth around the reef model increases with the increase of current speed. It can be observed that the scour depth increases rapidly from 20 mm to 31 mm and even 42 mm as the current speed increases evenly from 0.20 m s−1 to 0.22 m s−1 and then to 0.24 m s−1. However, when the current speed increases to 0.26 m s−1, i.e., close to the critical velocity (0.274 m s−1), the scour depth becomes 0.43 mm, increasing only 1 mm from the result at velocity of 0.24 m s−1.
|
|
Table 4 Equilibrium scour depth of four test runs in group Ⅰ at various current speeds |
In the present study, the current speed is less than the critical velocity, so the tests are all run under the state of 'clear water'. The sediment disturbance in the seabed is not so severe and the local scour around the reef model is small. The bed surface is flat, leading to a small final scour depth. When the current speed increases, the sand close to the model surface is actively lifted although no obvious deformation of the sand bed is observed in front of the model. Compared with the cases of low current speed, the scour depth is increased apparently. In general, the scouring depth increases with the increase in the current speed under the state of clear water scouring. When it is approaching the critical velocity, the growth rate of the scouring depth gradually slows down. Due to the limitation of the trial number, only a rough trend can be reported in the present study. More test runs are needed to accurately reveal the relationship between scour depth and current speed.
4.4 Effect of Cut-Opening on the Maximum Equilibrium Scour DepthAs the structure shape of reefs is considered, the cutopening is the main factor affecting scour, especially the open-area ratio (γ) and open-hole height (c). In this study, the side length of the octagonal opening cut on the cubic reef models is varied to offer five sets of models with different open-area ratios. Tested at a flow velocity of 0.22 m s−1, the results are shown in Table 5 and Fig.9. When the open-area ratio is 0, the maximum equilibrium depth is 40 mm. As the open-area ratio increases, the equilibrium depth gradually decreases. When the open-area ratio is 0.49, the equilibrium depth becomes 30 mm.
|
|
Table 5 Dimensionless scour depth and corresponding parameters under different opening conditions |
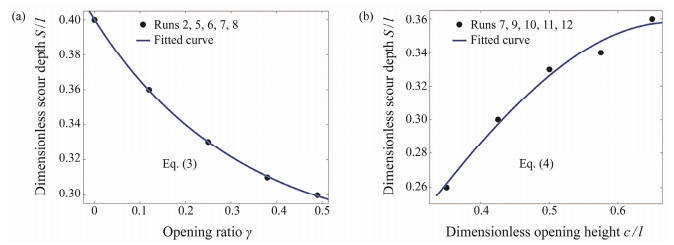
|
Fig. 9 Equilibrium scour depth plotted for models with various openings. (a), varying open-area ratio; (b), varying opening height. |
Similarly, open-hole height is various to obtain a group of models with same open-area ratio but different open-hole heights. As presented in Table 5 and Fig.9b, the equilibrium depth gradually increases as open-hole height increases. When open-hole height reaches 0.065 m, the maximum value of scour in this experiment is 0.036 m.
In order to obtain the empirical formula that equilibrium depth S is a function factor of the parameters γ and c respectively, the regression analyses are performed based on the processed data. The scour depth is expressed in a dimensionless form, i.e., S/l, where l is the side length of cubic reef models as defined before. Based on the previous research on caisson erosion (Zhao et al., 2012), and the comparisons of various fitting methods, two empirical formulas are obtained by the method of exponential regression fitting. The first one, relating the scour depth to the open-area ratio γ, is given in Eq. (3) with a coefficient of determination R2 = 0.9997:
| $ S/l = 0.1269 \times \exp (- 3.213\gamma) + 0.2732. $ | (3) |
On the other hand, the equation for the opening height c is given in Eq. (4) with a coefficient of determination R2 = 0.9996:
| $ S/l = 0.3597 \times \exp \left[ { - {{((c/l - 0.6606)/0.5473)}^2}} \right]. $ | (4) |
The curves for the above two exponential functions are also drawn in Fig.9.
The effect of the cut-opening on the scouring process is mainly associated with the impact of change in the flow patterns, such as the generation of descending flow, the formation of horseshoe vortices, and the turbulence of the side flow. When the testing reef model has a large cut-opening, the downward flow formed in front of the model is weak. It is not powerful enough to lift much sediments, which leads to a shallow scouring depth. In contrast, when the cutopening tends to small, a strong downward current is formed before the front surface of the model and large vortices are developed at the bottom, which causes a deep scouring depth.
Meanwhile, as the open-area ratios of the reef model increase, the blocking effect on the incoming flow decreases, allowing more incoming flow to pass through the reef with less block. This fact can be observed from the change in the drag coefficient Cd of the reef model. It has been reported that the drag coefficient Cd of reef decreases linearly with the increase in the open-area ratio (Tang et al., 2019). The drag coefficient indicates the blocking effect of the reef on the incoming flow. When the drag coefficient Cd decreases, the barrier effect of reefs on water flow is reduced, so that the incoming flow can pass through the reef more smoothly. The flow field is less changed by sea-bed obstacles and the scour depth decreases accordingly.
The mechanism of how the opening height affects the scouring process around the reefs is similar to the above description except that it does not change the water volume passing through the reef and the above discussion on the barrier effects cannot be applied here. The change in open-hole height mainly affects the velocity and pattern, causing downward flows. The scouring process is thus changed.
In the present work, considering the reduced material expenses and the collocations of reefs, the prototype of the cubic reef with an open-area ratio of 0.49 and open-height of 0.7 m is the optimal design for the minimum scour depth around cubic artificial reefs.
4.5 Effect of Bottom Angle on the Maximum Equilibrium Scour DepthFig.10 shows the effect of the bottom angle on the maximum equilibrium scour depth around the triangular reef. The results show that changes in the bottom angle of the triangular reef greatly affect local scour. The scour depth of the reef increases with the increase of the bottom angle. When the bottom angle is 30˚, the scour depth is only 9 mm. When the bottom angle rises to 90˚, the triangular reef becomes a cubic reef equivalently, and the scour depth reaches its maximum value, i.e., 41 mm. The variation in the bottom angle of the trapezoid reef can change the projected area heading the stream, which is a main impact on the local scour around the reef. In order to conduct a dimensionless analysis, the bottom angle is converted to a new dimensionless parameter, which is related to its sine function value. The corresponding results are shown in Table 6.
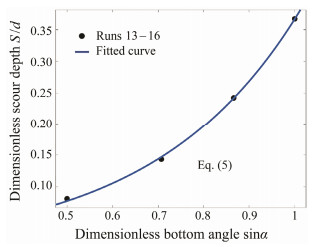
|
Fig. 10 Equilibrium scouring depth plotted against the slope of triangular reef. |
|
|
Table 6 Dimensionless scour depth and corresponding parameters caused by different bottom angles |
An empirical equation for the relationship between scour depth and the slope of the lateral plate is also derived, by means of the exponential regression method. It is presented in Eq. (5) with a coefficient of determination R2 = 0.9994.
| $ S/d = 0.01615 \times \exp (3.124\sin \alpha). $ | (5) |
The triangular artificial reef consists of three rectangular slabs. It is characterized by the large volume, low center of gravity, good stability, durable structure, and easy manufacturing. Compared with the other types of reefs, such as frame-type reefs, cylindrical reefs and composite reefs, the triangular artificial reef can maintain the integrity of its structure, no matter which side is in contact with the ground when placed on the seabed randomly. Thus, it is worthy of being popularized in the application of restoring offshore resources. The bottom of the triangular reef is not always completely enclosed by the sea bed. Some edges may still be exposed and form an additional base area. This unique design makes the scour depth much smaller than that of the cubic reef.
4.6 Comprehensive Selection of Reef OptimizationThe goal of our research is to optimize the reef design to reduce erosion. As mentioned earlier, artificial reefs might stir the flow passing by them. Disturbances in flow patterns result in upwelling and back eddy flow in the vicinity of reefs, which increase the productivity of marine life. These effects may be expressed by two indicators, the index of upwelling Iu and the efficiency index of the back eddy Iw. In our previous study, the effect of reef openings on the flow field has been detected (Wang et al., 2018). According to the results of that study, for single opening artificial reefs, the increase of open-area ratio γ tends to reduce the disturbance of ocean current, thereby reducing the value of two indicators Iu and Iw. For example, the value of Iu is reduced by 61.76% and that of Iw is reduced by 56.76% respectively when the open-area ratio increases from γ = 0.1 to γ = 0.5. Therefore, the function of reefs to disturb surrounding flow is weakened as the open-area ratio is increased. On the other hand, from the discussion in the previous subsection, increasing in the open-area ratio is to reduce scour around reefs. This means that the effect of change in open-area ratio is contradictory. It might worsen the performance of the reefs, although it is beneficial to reducing scour on the seabed. To optimize the reef design, it needs to make a good trade-off between these two incompatible conditions. Calculations are made for the models tested in our previous study by the empirical formula Eq. (4). The calculated scour depths for various values of γ are presented in Table 7 together with the values of indexes Iu and Iw obtained from previous experiments. A compromise should be made among these three terms and the maximum or minimum open-area ratio will not produce the best results. It is suggested that the open-area ratio between 0.2 to 0.3 might be a balanced choice for the design of ideal artificial reefs.
|
|
Table 7 The index of upwelling Iu, the efficiency index of the back eddy Iw, and the calculated scour depth S0 of the reefs with different open-area ratios |
In the present study, the effects of local scour on the artificial reefs are studied in the flume. In these experiments, the scour history around artificial reefs is explored, the seabed shape after scouring is scanned, and the factors that affect scouring are examined. The results of the flume experiments agree well with the previous prediction and actual observations. Regression analysis models are used to study the influence on equilibrium scour depth caused by the current speed and various reef shapes, such as the openarea ratios and height of the opening hole for a cubic artificial reef, as well as the bottom angle for a triangular artificial reef. Moreover, the empirical equations are proposed, which are the preliminary study on the local scour around the artificial reefs. More researches should be done to verify the formulas by means of the model experiments and the numerical simulations in the future work.
A brief summation is given as follows.
1) The scouring process develops in three stages, including the initial stage, the development stage and the equilibrium stage. The current speed does not affect the time to reach the equilibrium provided scouring under the clear water state. In the present study, the time to reach equilibrium is about 7 h no matter what value the current speed is. After reaching scouring equilibrium, the seabed around the reef is basically symmetric with respect to the centerline of the reef. The maximum scour depth appears at the scour pits close to the sharp corners of the upstream surface while the scour depth on the two sides of the reef is shallow.
2) Under the condition of erosion without sediment movement, the scouring depth around the reef increases with the increasing flow velocity. According to the experiment results, a sea area with a relatively slow current can be selected as the reef throwing area, which can effectively reduce local scour around the reef body.
3) Both the open-area ratio and the open-hole height significantly influence the local scour around the cubic artificial reef. In the present work, considering the reduced material expenses and the collocations of reefs, the prototype of the cubic reef with an open-area ratio of 0.49 and openheight of 0.7 m is the optimal design combination for the minimum scour depth around cubic artificial reefs.
4) Considering the effect of the opening on local scour with the upwelling and back eddies in the flow field around cubic artificial reefs, the artificial reef with an open-area ratio of 0.25 can produce large upwelling and back eddies but a small scour depth, which may be a good choice for the sustainable development of artificial reefs.
5) The bottom angle of the triangular artificial reef has a significant effect on local scour since it changes the effective area of the frontal surface facing the incoming flow. The degree of scour decreases as the bottom angle is reduced. In a sea area where scour is likely to occur due to seabed condition and current speed, the triangular reef with a small bottom angle will be a good choice for the design of an anti-scour reef.
AppendixThe shear stress θs acting on the particles in the seabed plays an important role in the field of sediment erosion. It is usually measured by a nondimensional form, i.e., the Shields parameter, which is defined as:
| $ {\theta _s} = \frac{{{\tau _s}}}{{\rho g(s - 1){d_{50}}}}, $ | (A-1) |
where τs is the shear stress experienced by the sea bed; ρ is the water density; g is the acceleration due to gravity; s is the specific gravity of sand; d50 denotes the median particle size of sand. It is a criterion to calculate the initiation of sediment motion in a fluid flow. The critical value can be determined as follows (Soulsby and Whitehouse, 1997):
| $ {\theta _{Cr}} = \frac{{0.30}}{{1 + 1.2{D_*}}} + 0.055\left[ {1 - \exp (- 0.020{D_*})} \right], $ | (A-2) |
where D* is the nondimensional particle size defined as D* = [g(s−1)/ν2]1/3d50 with ν as the kinematic viscosity of fluid. The physical properties of the sand used in the experiments are given in Table 8. Accordingly, the critical Shields parameter may be figured out as θCr = 0.0484. This value is used to judge whether sediment erosion is under the state of clear-water or live-bed according to the condition θs /θCr < 1 or θs /θCr ≥ 1.
|
|
Table 8 Parameters used in the tests |
As the shear stress τs is considered to be mainly caused by the skin friction between the fluid and seabed, an empirical formula, based on a flat sand surface, is adopted to estimate the stress value (Yao et al., 2018).
| $ {\tau _s} = \rho {C_D}{\overline U ^2}, $ | (A-3) |
where
Combining Eqs. (A-1) with (A-3) and giving the critical Shields parameter above, the critical flow velocity can be calculated as:
| ${\overline U _{Cr}} = \sqrt {\frac{{{\theta _{Cr}}g(s - 1){d_{50}}}}{{{C_D}}}} = 0.274\ ({\rm{m\ s}}^{−1}).$ | (A-4) |
The calculated value is shown in Table 8. In the present study, this is a criterion to judge whether a test is performed under the state of clear-water or live-bed according to the flow velocity less or greater than the critical velocity.
AcknowledgementsThe study is supported by the National Key R & D Program of China (No. 2019YFD0901302), and the National Natural Science Foundation of China (No. 32073025).
Bao, T., and Liu, Z.. 2017. Vibration-based bridge scour detection: A review. Structural Control & Health Monitoring, 24(7): 19. DOI:10.1002/stc.1937 (  0) 0) |
Bauri, K. P., and Sarkar, A.. 2016. Flow and scour around vertical submerged structures. Sadhana-Academy Proceedings in Engineering Sciences, 41(9): 1039-1053. DOI:10.1007/s12046-016-0539-y (  0) 0) |
Baykal, C., Sumer, B. M., Fuhrman, D. R., Jacobsen, N. G., and Fredsoe., J.. 2015. Numerical investigation of flow and scour around a vertical circular cylinder. Philosophical Transactions of the Royal Society A–Mathematical Physical and Engineering Sciences, 373(2033): 20140104. DOI:10.1098/rsta.2014.0104 (  0) 0) |
Castro, I. P., and Robins, A. G.. 1977. The flow around a surfacemounted cube in uniform and turbulent streams. Journal of Fluid Mechanics, 79(2): 307-335. DOI:10.1017/S0022112077000172 (  0) 0) |
Chatanantavet, P., and Lamb, M. P. J., 2014. Sediment transport and topographic evolution of a coupled river and river plume system: An experimental and numerical study. Journal of Geophysical Research Earth Surface, 119 (6): DOI: 0.1002/2013JF002810.
(  0) 0) |
Chiew, Y. M., 1984. Local scour at bridge piers. PhD thesis. University of Auckland.
(  0) 0) |
Dey, S., and Barbhuiya, A. K.. 2005. Flow field at a vertical-wall abutment. Journal of Hydraulic Engineering, 131(12): 1126-1135. DOI:10.1061/(ASCE)0733-9429(2005)131:12(1126 (  0) 0) |
Ding, L., Wang, J. M., Tang, Z. C., Chen, H. G., and Jia, X. P.. 2019. Model test and analysis of local scouring of artificial reefs on silt seabed under the action of water flow. Journal of Fisheries, 43(9): 2015-2024 (in Chinese with English abstract). (  0) 0) |
Gao, D. G., Tian, W. P., Zhang, Y. Q., and Wang, Y. L.. 1998. Scour mechanism and scour depth of abutments. China Journal of Highway and Transport, 11(1): 54-62 (in Chinese with English abstract). DOI:10.19721/j.cnki.1001-7372.1998.01.009 (  0) 0) |
Keshavarzi, A., Shrestha, C. K., Melville, B., Khabbaz, H., and Ball, J.. 2018. Estimation of maximum scour depths at upstream of front and rear piers for two in-line circular columns. Environmental Fluid Mechanics, 18(3): 537-550. DOI:10.1007/s10652-017-9572-6 (  0) 0) |
Kim, D., Woo, J., Yoon, H. S., and Na, W. B.. 2016. Efficiency, tranquillity and stability indices to evaluate performance in the artificial reef wake region. Ocean Engineering, 122: 253-261. DOI:10.1016/j.oceaneng.2016.06.030 (  0) 0) |
Lin, Y. J., and Lin, C.. 2020. Scour effects on lateral behavior of pile groups in sands. Ocean Engineering, 208: 107420. DOI:10.1016/j.oceaneng.2020.107420 (  0) 0) |
Liu, Q. S., Tang, H. W., Wang, H., and Xiao, J. F.. 2018. Critical velocities for local scour around twin piers in tandem. Journal of Hydrodynamics, 30(6): 1165-1173. DOI:10.1007/s42241-018-0122-6 (  0) 0) |
Melville, B. W., and Sutherland, A. J.. 1988. Design method for local scour at bridge piers. Journal of Hydraulic Engineering, 114(10): 1210-1226. DOI:10.1061/(ASCE)0733-9429(1988)114:10(1210 (  0) 0) |
Nguyen, V. B., Nguyen, Q. B., Zhang, Y. W., Lim, C. Y. H., and Khoo, B. C.. 2016. Effect of particle size on erosion characteristics. Wear, 348-349: 126-137. DOI:10.1016/j.wear.2015.12.003 (  0) 0) |
Pandey, M., Sharma, P. K., Ahmad, Z., and Singh, U. K.. 2017. Evaluation of existing equations for temporal scour depth around circular bridge piers. Environmental Fluid Mechanics, 17: 981-995. DOI:10.1007/s10652-017-9529-9 (  0) 0) |
Petersen, T. U., Sumer, B. M., Fredsoe, J., Raaijmakers, T. C., and Schouten, J. J.. 2015. Edge scour at scour protections around piles in the marine environment–Laboratory and field investigation. Coastal Engineering, 106: 42-72. DOI:10.1016/j.coastaleng.2015.08.007 (  0) 0) |
Singh, S. K., Debnath, K., and Mazumder, B. S.. 2016. Turbulence statistics of wave-current flow over a submerged cube. Journal of Waterway Port Coastal and Ocean Engineering, 142(3): 04015027.1-04015027.20. DOI:10.1061/(asce)ww.1943-5460.0000329 (  0) 0) |
Soulsby, R. L.. 1997. Dynamics of Marine Sands: A Manual for Practical Applications. Thomas Telford Publications, London, 249pp.
(  0) 0) |
Soulsby, R. L., and Whitehouse, R. J. S. W., 1997. Threshold of sediment motion in coastal environments. Proceedings of the 13th Australasian Coastal and Engineering Conference and 6th Australasian Port and Harbour Conference. Cristchurch, New Zealand.
(  0) 0) |
Sumer, B. M., and Fredsøe, J.. 2002. The Mechanics of Scour in the Marine Environment. World Scientific Press, 69pp.
(  0) 0) |
Sumer, B. M., Christiansen, N., and Fredsoe, J.. 1992. Time scale of scour around a vertical pile. Scour, 3: 308-315. (  0) 0) |
Tang, Y. L., Yang, W. Z., Sun, L. Y., Zhao, F. F., and Long, X. Y.. 2019. Studies on factors influencing hydrodynamic characteristics of plates used in artificial reefs. Journal of Ocean University of China, 18(1): 197-206. DOI:10.1007/s11802-019-3706-z (  0) 0) |
Tavouktsoglou, N. S., Asce, A. M., Harris, J. M., Asce, M., Simons, R. R., and Whitehouse, R. J. S. J.. 2017. Equilibrium scour-depth prediction around cylindrical structures. Journal of Waterway Port Coastal & Ocean Engineering, 143(5): 1-19. DOI:10.1061/(ASCE)WW.1943-5460.0000401 (  0) 0) |
Wang, G., Wan, R., Wang, X. X., Zhao, F. F., Lan, X. Z., Cheng, H., et al.. 2018. Study on the influence of cut-opening ratio, cut-opening shape, and cut-opening number on the flow field of a cubic artificial reef. Ocean Engineering, 162: 341-352. DOI:10.1016/j.oceaneng.2018.05.007 (  0) 0) |
Wang, S. Y., Wei, K., Shen, Z. H., and Xiang, Q. Q.. 2019. Experimental investigation of local scour protection for cylindrical bridge piers using anti-scour collars. Water, 11(7): 19. DOI:10.3390/w11071515 (  0) 0) |
Yang, Y., Melville, B. W., Macky, G. H., and Shamseldin, A. Y.. 2019. Local scour at complex bridge piers in close proximity under clear-water and live-bed flow regime. Water, 11(8): 1530. DOI:10.3390/w11081530 (  0) 0) |
Yang, Y. L., Qi, M. L., Wang, X., and Li, J. Z.. 2020. Experimental study of scour around pile groups in steady flows. Ocean Engineering, 195(12): 106651. DOI:10.1016/j.oceaneng.2019.106651 (  0) 0) |
Yao, W., An, H., Draper, S., Cheng, L., and Harris, J. M.. 2018. Experimental investigation of local scour around submerged piles in steady current. Coastal Engineering, 142: 27-41. DOI:10.1016/j.coastaleng.2018.08.015 (  0) 0) |
Yu, T., Lian, J., Shi, Z., and Wang, H.. 2016. Experimental investigation of current-induced local scour around composite bucket foundation in silty sand. Ocean Engineering, 117: 311-320. DOI:10.1016/j.oceaneng.2016.03.045 (  0) 0) |
Yun, D. H., and Kim, Y. T.. 2018. Experimental study on settlement and scour characteristics of artificial reef with different reinforcement type and soil type. Geotextiles & Geomembranes, 46(4): 448-454. DOI:10.1016/j.geotexmem.2018.04.005 (  0) 0) |
Zhao, M., Zhu, X., Cheng, L., and Teng, B.. 2012. Experimental study of local scour around subsea caissons in steady currents. Fuel and Energy Abstracts, 60: 30-40. DOI:10.1016/j.coastaleng.2011.08.004 (  0) 0) |
 2022, Vol. 21
2022, Vol. 21



 (Run 8)
(Run 8) (Run 2)
(Run 2) (Run 7)
(Run 7) (Run 14)
(Run 14)