2) School of Civil Engineering, Tianjin University, Tianjin 300072, China
The global energy crisis has experienced further intensification, which resulted in the increasing prominence of the shortage of onshore oil and gas resources. The world's oceans contain abundant oil and gas resources (Malde et al., 2020). Being the largest marine industry, the total offshore oil and gas account for one-third of the total value of the marine economy (Jouffray et al., 2020); offshore oil production accounted for 34% of the total oil production in 2004 and rose to 48% in 2020 (China Commercial Industry Research Institute, 2020). Therefore, the problem of energy shortage can be addressed through the development of offshore oil and gas resources, which is of great practical significance. The wellhead platform represents a crucial exploration device applied in offshore oil and gas production. At present, marginal oil fields account for the bulk of the discovered oil and gas resources. However, the risk of investment in the development of marginal oil fields is large, and the profit is small. Therefore, a simple, economical, effective, and reliable platform is essential for the development of marginal oil fields.
The bucket foundation gains favor due to its advantages, such as high bearing capacity, low cost, and convenient installation. Other practical engineering projects have applied bucket foundations to offshore platforms, and a batch of simple bucket foundation platforms were constructed. Fig.1 shows the CFD18-1 and JZ9-3 bucket foundation wellhead platforms, which adopt the three-bucket jacket foundation, and their installation in 2008 (Shan et al., 2011).

|
Fig. 1 Engineering applications of wellhead platforms with bucket foundations. |
Most scholars have performed relevant studies on the working performance of wellhead platforms. Qiu et al. (2022) established a drilling platform/riser/wellhead/conductor fully coupled dynamic model in the evaluation of dynamic stability of subsea wellhead system and proposed an algorithm to solve the fully coupled dynamic model based on finite element and Newmark integral method. Li et al. (2023) proposed a cylindrical floating, drilling, production, storage and offloading unit platform based on the platform of floating work over production storage and offloading system and added an extension cylinder and a new damping structure at the bottom; their hydrodynamic performances are calculated using the potential theory and compared with the frequency domain. Deng et al. (2019) investigated the bending moment of a deep-water subsea wellhead-shallow casing system induced by risers under the effects of offshore platform drifting and current and wave forces. Ruschel et al. (2021) proposed the utilization of the Univariate Dimension Reduction Method to compute the fatigue damage in wellhead structures. Wang and Gao (2022) established the mechanical model of the drilling system by considering the drilling riser – subsea wellhead – conductor as a whole research object to obtain the marine environmental constraints of deepwater drilling operations.
Some scholars have conducted studies on the construction process of wellhead platforms. Zhang et al. (2022) established mechanical models and governing equations based on various tubular system properties of distinct stages and solved the tubular mechanics in distinct installation processes by coupling lateral displacement boundary conditions at varied pipe string connections. The mechanical model by Wang and Gao (2021) established the mechanical model and deduced the governing equation to illustrate the static mechanics of the tubular system regarding surface casing installation, in which the model considers the gravity, buoyancy force, lateral wave-current force, and the top horizontal displacement of the floating drilling vessel.
The current research on wellhead platforms is mainly focused on the safety of their working and construction processes. However, less research has been conducted during its transportation process because traditional wellhead platforms are mostly fixed. The further development of marginal oil fields has resulted in the gradually increasing demand for movable and reusable wellhead platforms. Thus, an integrated wellhead platform with a bucket foundation will occupy a widespread application market and attain a good development prospect in the future through its integrated transportation, low cost, convenient installation, and recyclability (Wang, 2008; Li and Gao, 2013; Cui, 2014).
The integrated rounded rectangular wellhead platform with a bucket foundation consists of a rounded rectangular bucket, an arc-shaped transition section, and an upper wellhead platform (Fig.2). The rounded rectangular bucket foundation has an interior that is divided into compartments and a middle compartment without roof and is connected to the interior of the transition section, which is convenient for operation of drilling ships. The remaining compartments are closed at the top and open at the bottom, their structure enables integrated towing transportation and one-step installation (Ding et al., 2012, 2016a; Zhang et al., 2014); in addition, the bucket foundation for wellhead platform is designed to greatly simplify the offshore installation process and reduce the construction cost (Chu, 2012; Yu et al., 2020; Zhao et al., 2020).

|
Fig. 2 Integrated wellhead platform withabucket foundation. |
Some scholars have conducted relevant research based on the features of the integrated floating transportation of the bucket foundation. Le et al. (2012) conducted towing tests on a 1:20 scaled platform model with a four-bucket foundation with various angles of the trim formed by the stern in the following and head sea. In addition, the towing process of the bucket foundation platform was tested to determine the acceleration, internal air pressure, bottom water pressure of the bucket, and towing force of the platform. Ding et al. (2008) considered the bucket foundation offshore platform as the research object and conducted measurements of the platform acceleration, towing force, air pressure in the bucket, and water pressure at the bottom of the bucket under various towing combinations via a model test; then, they analyzed the test results on 10 mechanical parameters through factor and cluster analyses. Ding et al. (2022) investigated the effects of water depth and towing speed on the liquid level, compartment pressure, and pitch angles during the towing of composite bucket foundations based on field measurements data from a 3.3 MW offshore wind-power project in China. According to Ding et al. (2019), the basic hydrodynamic characteristics of the composite bucket foundation can be computed in the frequency domain and adopted multiple random wave models to assess the influence of wave heights, periods, and spectral peak factors on towing motion features of composite bucket foundation. Zhang et al. (2015) investigated the wet tow of a dedicated vessel with two bucket foundations and the upper offshore wind turbines; they performed a series of field experiments of varied air pressures inside the bucket foundations and various vessel ballasts and examined the motion behaviors of the dedicated vessel. Yan et al. (2021) introduced a new integrated wet-towing method for a 'jacket + triple-bucket foundation' composite structure based on a 6.7 MW triple-bucket jacket foundation (TBJF) project at a deep-sea wind farm in China; the method is suitable for far long-distance transportation in far-offshore applications. Zhang et al. (2019) used numerical simulation to assess the effects of draft, speed, and wave height on the towing stability of wind turbine transportation vessels in the frequency and time domains.
In this paper, the test method was used to investigate the motion response of a rounded rectangular wellhead platform with a bucket foundation during floating transformation; in addition, analysis was also focused on the feasibility of the integrated towing of the wellhead platform with bucket foundation and the influence of various factors on its floating stability (Ding et al., 2016b; Min, 2018). In addition, the Apriori algorithm was applied in the analysis of the influence of various factors on the structure's floating stability, and the influence law and mechanism of single factors on the integrated wellhead platform were obtained.
2 Design of Test 2.1 Test SiteThe model test was performed in the Tianjin University Port and Marine Engineering Test Pool, whose length, width, and depth of the pool amount to 55 m × 40 m × 1.8 m, as shown in Fig.3. The low-inertia AC servo wave pusher was used to make waves in the pool. The wave period can be controlled within 0.5 – 5.0 s, with the maximum wave height reaching 0.5 m. A wave energy absorption device is installed at the end of the pool. Based on the main dimensions of the test object and pool size, the selected scale ratio of the test model is λ = 1:30, with the water depth of the test pool set at 1.0 m.

|
Fig. 3 Test site. |
The model test was conducted in accordance with the similarity criterion, in which geometric, motion, gravity, and inertial force similarities must be satisfied.
In accordance with the similarity criterion, Froude and Strouhal numbers of the prototype and the model should be equal, i.e.:
| $ \frac{\mathit{λ}_{v}^{2}}{\mathit{λ}_{g} \mathit{λ}_{L}}=1, \frac{\mathit{λ}_{v} \mathit{λ}_{t}}{\mathit{λ}_{L}}=1, $ |
where λv refers to the similarity ratio of velocity, λg denotes the similarity ratio of gravity acceleration, λt indicates the similarity ratio of time, and λL represents the similarity ratio of length.
Based on the motion similarity, the time similarity ratio is $\mathit{λ}_{t}=\mathit{λ}_{L}^{0.5}$, the velocity scale is
In accordance with the similarity criterion, the designed model structure had a length ratio of 1:30. Table 1 provides a summary of the similarity of each physical quantity. To achieve the similar heights of the center of gravity and the moment of inertia, we placed the corresponding counterweight on the top of the model.
|
|
Table 1 Model structure parameters (1:30) |
Fig.4 shows the schematic of the internal division of the model structure. Seven compartments were considered under the transition section, and the middle compartment lacked a roof for communication with the interior of the transition section. Fig.5 shows the physical image of the model structure.
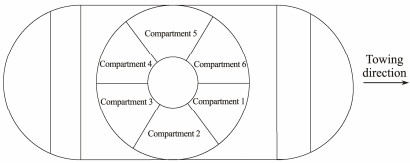
|
Fig. 4 Schematic of the internal division of the model. |

|
Fig. 5 Physical images of the test model. |
The devices used in this test comprised two Donghua dynamic acquisition instruments, six barometers, one tension sensor, one inclinometer, one triaxial acceleration sensor, and one wave height meter. The barometer was used to measure air pressure in each compartment, the tension sensor to determine the towing force, the inclinometer to monitor the swing motion of the structure during towing, the triaxial acceleration sensor to measure the structure's motion acceleration, and the wave height meter to measure wave height. Table 2 and Fig.6 provide the test sensors and Fig.7 displays the layout of sensors.
|
|
Table 2 Test devices |

|
Fig. 6 Physical images of test devices. |
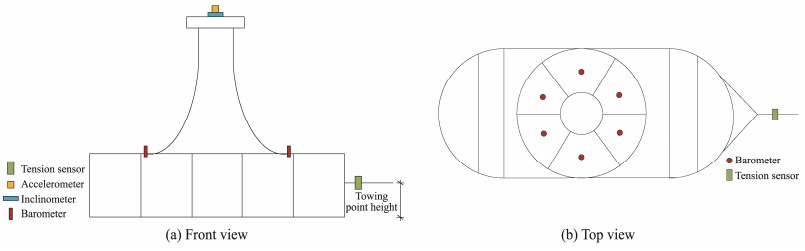
|
Fig. 7 Layout of test sensors. |
The test included still water and wave tests, with the wave test comprising regular and irregular wave tests. Table 3 displays the test conditions. Condition 1 referred to the standard group of the still water test, and condition 12 indicated the standard group of the wave test. Each test condition involved a towing speed of 32 cm s−1 and the corresponding prototype speed of 0.55 cm s−1. The model wave heights of 2.5, 7.5, 10, and 12.5 cm corresponded to the prototype wave heights of 0.75, 2.25, 3.0, and 3.75 m, respectively. In addition, the model wave periods of 1.1, 1.6, and 1.9 s corresponded to the prototype wave periods of 6.0, 8.8, and 10.4 s, respectively. In addition, the JONSWAP wave (Yu et al., 2017) was selected as the irregular wave, and its wave parameters in the test condition table were significant wave height and average period. The variables investigated in the test consisted of draft, towing point height, wave height, and wave period.
|
|
Table 3 Test condition |
The integrated wellhead platform generates buoyancy through water discharge through the bucket wall and the air inside the bucket. First, free attenuation tests of the structure, including roll, pitch, and heave attenuation tests, were carried out. The initial draft of the structure was set to 20 cm, and the initial rotational displacements were applied on the foundation along the horizontal (x and y direction) and vertical linear direction (z direction), respectively. Then, the structure was released, the sway attenuation of the structure was recorded, and the obtained results were normalized to determine the roll, pitch, and heave attenuation curve. The normalized curves were transformed via the Fourier method to acquire the natural frequencies of the roll, pitch, and heave (Fig.8). The roll had a natural frequency and period of 0.5 Hz and 2.0 s, respectively. The pitch showed a natural frequency and period of 0.688 Hz and 1.45 s, respectively. Heave has a natural frequency of 0.714 Hz and a natural period of 1.40 s.
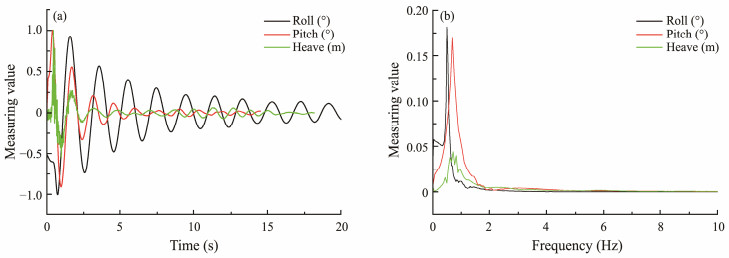
|
Fig. 8 Normalized attenuation curve (a) and spectrum diagram of attenuation curve (b). |
Half-power bandwidth method was used to determine the damping ratio, and a Fourier transform was performed on the free attenuation curve to obtain the frequency response curve (Fig.9). The damping ratio can be calculated as $\xi=\frac{f_{2}-f_{1}}{f_{2}+f_{1}}$, where ξ indicates the damping ratio, and f1 and f2 are shown in Fig.9. The roll, pitch, and heave had damping ratios equal to 0.06, 0.11, and 0.20, respectively.
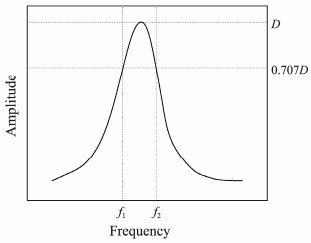
|
Fig. 9 Frequency response curve of free attenuation. |
First, an investigation was conducted on the motion response of the wellhead platform with a bucket foundation during the towing process in still water. The draft and mooring point height of the wellhead platform with a bucket foundation were changed, and the influence of these factors on the motion response when towing in still water was examined.
4.1 Motion Response of Standard Group in Still WaterCondition 1 was set as the standard group in still water, and the standard group's motion response is shown in Fig.10. In addition, the standard group had a maximum rolling angle of 0.44˚ and an average value of 0.026˚. This group also had a maximum pitch angle of 1.50˚ and an average value of 1.0˚. The maximum heave acceleration reached 0.035 m s−2, with an average value equal to 0.008 m s−2. The maximum towing force was 2.29 N, and the average value was 1.4 N.
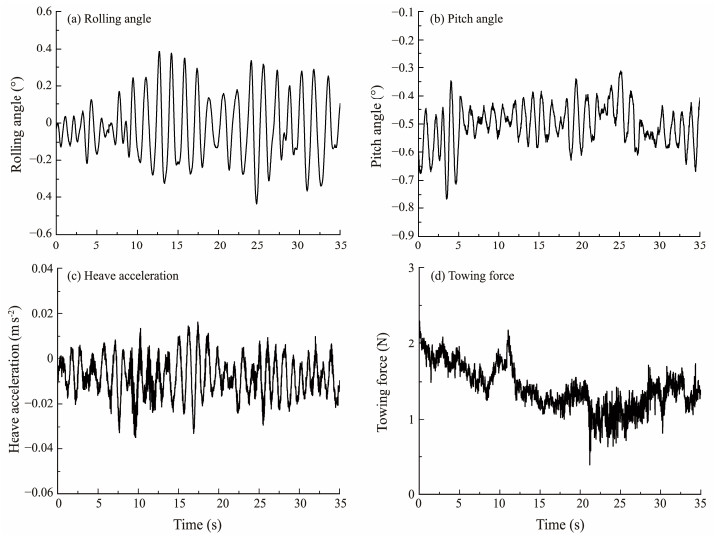
|
Fig. 10 Motion response of the standard group in still water. |
The internal air cushion generates air pressure, providing buoyancy to air floating structure. The difference between an air-floating structure and its solid counterpart is that an air cushion spring was added to the water cushion spring air-floating structure. The air pressure in the compartment determined the stiffness of the air cushion and directly affected the motion response of the structure. Therefore, the pressure inside the compartment of the structure should be studied. Fig.11 displays the air pressure in each compartment of the standard group. The air pressures in Compartments 1 and 6 were considerably higher than those in other compartments due to the effect of cable traction. The bucket foundation of the wellhead platform exhibited a forward inclination, causing the position close to the towing point to tilt downward and the position distant from the towing point to float upward. Thus, the front compartments (Compartments 1 and 6) presented a high internal pressure, and that of the rear compartments (Compartments 3 and 4) was lower. Compared with the front and rear compartments, the middle compartment exhibited a smaller fluctuation range of the interior pressure. The air pressure data of multiple groups of tests presented a similar distribution pattern; thus, in follow-up research, the air pressure of Compartment 1 was obtained and considered as the research object.
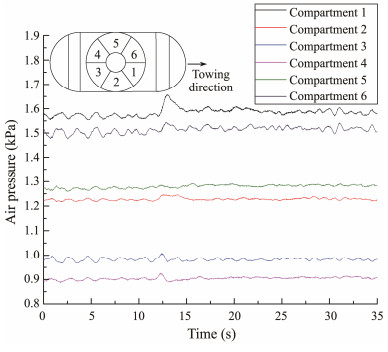
|
Fig. 11 Air pressure inside each compartment for the standard group. |
Fig.12 displays the motion response of the wellhead platform with a bucket foundation under various drafts during the towing processes in still water. The roll response of the structure during still water towing was insensitive to the draft, and the pitch, heave, towing force, and air pressure were highly sensitive to the draft. With the increase in the draft, the pitch angle first decreased and then increased. The average pitch angle reached 1.4˚, 0.5˚, and 1.0˚ when the drafts were 15, 20, and 25 cm, respectively. The pitch angle was consistently negative, which means that the structure maintained the forward tilt during the still water towing process. Fig.13 shows the force diagram during the forward tilt of the structure. T in the figure denotes the towing force, F indicates the towing resistance; Pi means the increased air pressure due to forward tilt of the structure, and Pr corresponds to the decreased air pressure due to forward tilt of the structure. G represents the self-weight of the structure, FB indicates the buoyancy of the structure. The resultant moment of towing force T and towing resistance F caused the structure to tilt forward, and the pressure difference in various compartments ∇P = Pi − Pr caused the center of buoyancy to move forward. Thus, buoyancy and gravity formed a resistance moment to prevent the tilting structure. The air pressure in the compartment decreased with the increase of the draft. Thus, the greater the draft, the smaller the air cushion stiffness and the smaller the corresponding resistance moment. On the other hand, given the height of the towing point at 20 cm, when the draft depth increased from 15 cm to 25 cm, the lever arm of the towing force and towing resistance gradually decreased. During the increase in the draft from 15 cm to 20 cm, the reduction of overturning moment plays a major role, and the pitch angle of the structure decreases. When the draft was increased from 20 cm to 25 cm, the reduction of air cushion stiffness was dominant, the greater reduction of resistance moment than that of overturning moment, and the structure pitch angle increased. The air pressure decreased with the increase in the draft. When the draft increased from 15 cm to 25 cm, the average air pressure decreased from 1.9 kPa to 1.38 kPa, and the standard deviation decreased from 0.011 kPa to 0.009 kPa. The average towing force increased from 1.09 N to 2.5 N, with the standard deviation increasing from 0.23 N to 0.35 N. The range of heave acceleration fluctuation increased, the standard deviation increased from 0.006 m s−2 to 0.016 m s−2, and the average value was almost unchanged.
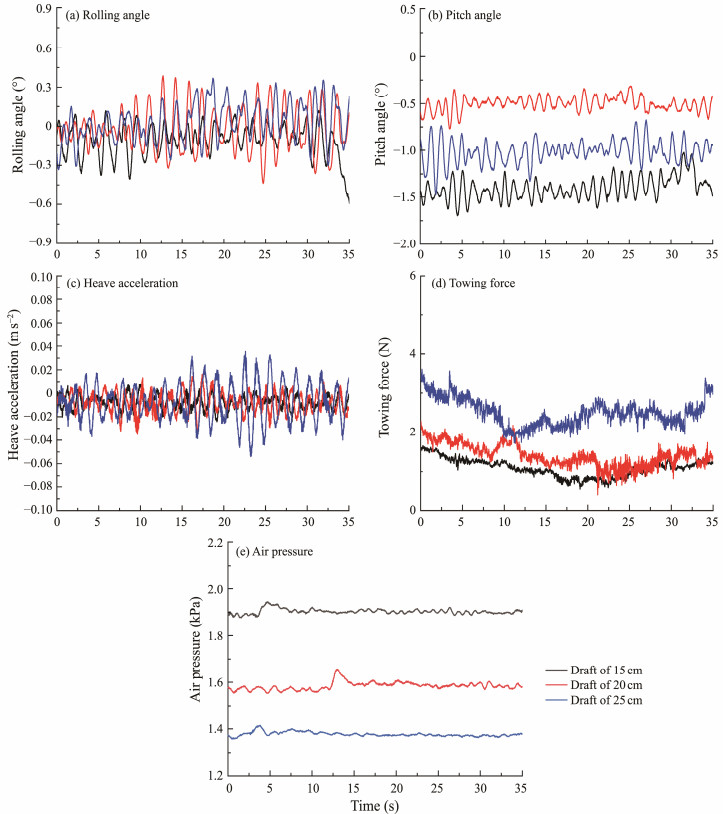
|
Fig. 12 Motion responses at various drafts during towing in still water. |
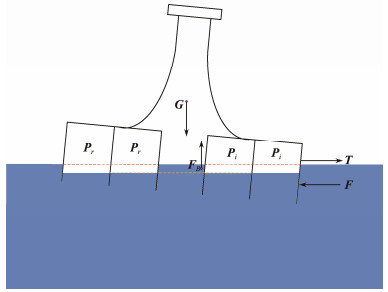
|
Fig. 13 Forces on structure in the forward tilt state. |
Fig.14 shows the motion response of the integrated wellhead platform at various towing point heights during the towing process in still water. With the increase in the height of the towline point, the pitch angle, towing force, and air pressure in the compartments gradually increased, while the fluctuation ranges of the heave acceleration became smaller, and the average value of heave acceleration remained unchanged. With the increase in the height of the towing point from 10 cm to 20 cm, the average rolling angle decreased from 0.11˚ to 0.02˚, and the standard deviation decreased from 0.32˚ to 0.13˚. The average pitch showed an increase from 0.13˚ to 0.5˚ and minimal stages in the standard deviation changed. The pitch angle constantly showed negative values, which means a constant forward tilt attitude of the structure, and the pitch angle fluctuated around 0˚ when the height of the towing point was 10 cm, which means that the structure was in horizontal posture at this time. Given that the draft of the structure was 20 cm, and the towing point was at the center of the flow impact surface when the height of the towing point was 10 cm, basically no bending moment can be found in the pitch direction. The average heave acceleration remained unchanged, and the standard deviation was reduced from 0.02 m s−2 to 0.009 m s−2. The average towing force and its standard deviation increased from 0.65 N to 1.41 N and from 0.23 N to 0.29 N, respectively. The average pressure increased from 1.39 kPa to 1.58 kPa, and its standard deviation decreased from 0.02 kPa to 0.016 kPa.
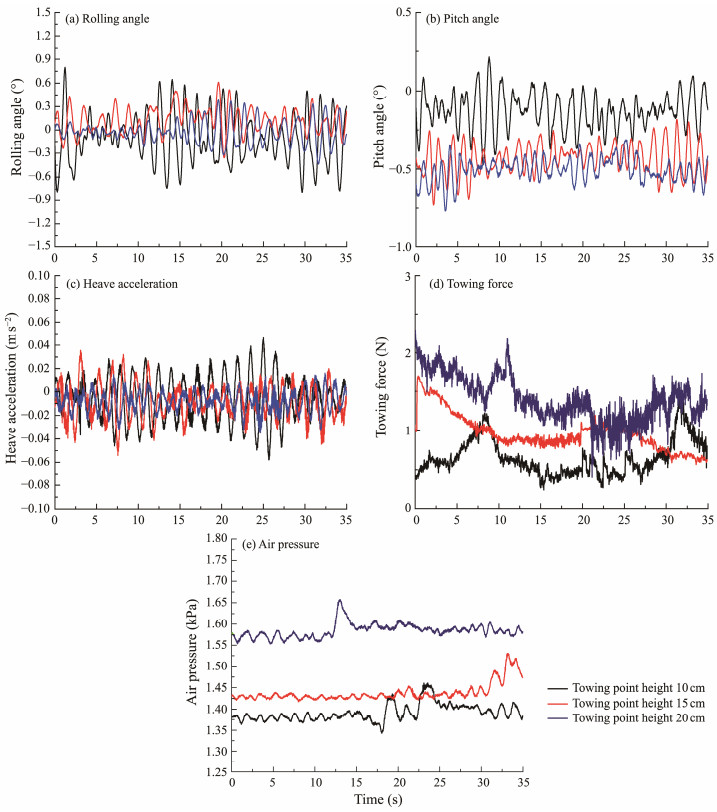
|
Fig. 14 Motion responses at various towing point heights in still water. |
The towing test in waves comprises towing in regular and irregular waves, whose results will be analyzed as follows.
5.1 Towing Test in Regular WaveThe influencing factors, such as draft, mooring point height, wave height, and wave period, were taken as variables. In addition, their motion responses to different conditions when towing in regular water are studied.
5.1.1 Influence of draft on regular wave towingFig.15 reveal the motion response of the wellhead platform with bucket foundation under various drafts during towing in regular waves. Fig.16 reveals the statistical values of motion responses at various drafts in regular waves. The rolling angle changes slightly under different drafts. When the draft increased from 15 cm to 25 cm, the average pitch angle during towing in regular waves remained unchanged, the standard deviation decreased from 18.30˚ to 10.48˚, and a negative average pitch angle was obtained, that is, the structure had a greater forward inclination than the backward reclination due to the traction of towing cable. The average heave acceleration was unchanged, and the standard deviation decreased from 0.81 m s−2 to 0.48 m s−2. The average towing force and standard deviation decreased from 6.22 N to 4.89 N and from 4.61 N to 4.58 N, respectively. The average air pressure decreased from 2.93 kPa to 1.76 kPa, and the standard deviation increased from 0.27 kPa to 0.40 kPa. Under regular waves, with the increase in the draft, the compartment pressure decreased, the range of pitch angle oscillation decreased, and the heave acceleration and towing force diminished. In addition, the relationship between the initial tension under various drafts was consistent with that in still water, i.e., the larger the draft, the larger the initial tension, which indicates that the submerged area still dominated the initial towing force.
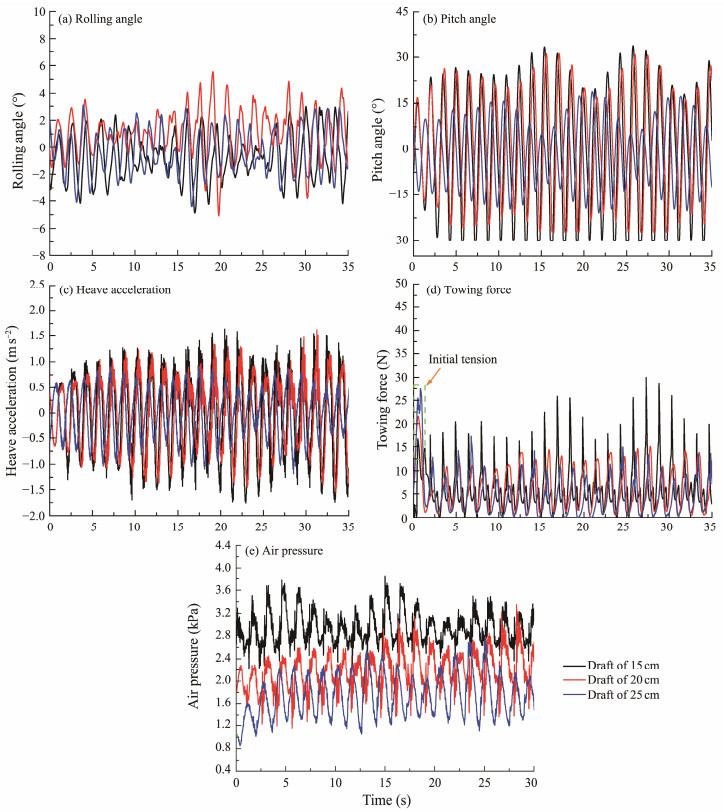
|
Fig. 15 Motion responses at various drafts in regular waves. |
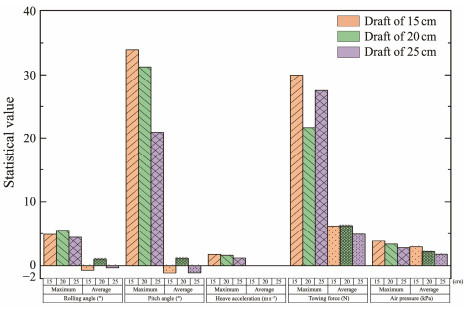
|
Fig. 16 Statistical values of motion at various drafts in regular waves. |
Table 4 shows the various motion modes of the structure in regular waves compared with those in still water. The main differences were the various change rules of pitch angle and towing force. During the towing process under waves, the pitch angle fluctuated at approximately 0˚, which indicates that the structure did not consistently tilt forward but was in a cycle of forward-backward-forward reciprocating motion. In addition, the towing force oscillated in the form of a pulse. Moreover, the effect of draft depth on the motion response of towing in regular waves varied from that in still water. When towing in still water, the pitch angle decreased and then increased with the increase in the draft. Meanwhile, the pitch angle gradually decreased as the draft depth increased during towing in waves because although the submerged area of the structure increased when the draft was large, the effect of the wave on the structure above the water surface became smaller. Thus, the larger the draft, the lower the center of gravity of the structure, and the better the towing stability, all of which result in a small pitch angle. The variation law of the towing force in regular waves varied from those in still water. During wave towing, the structure experienced periodic transient impact force, whose magnitude was directly related to the structure's motion response. When the draft was 15 cm, the structure tilted forward to a large extent, which caused an increase in the flow impact area and towing resistance. In addition, the smaller the draft, the greater the sway angle of the structure, the poorer the towing stability, and the greater the instantaneous impact force imposed by the cable on the structure. Therefore, the pulse effect of the towing force was the most evident at the draft value of 15 cm.
|
|
Table 4 Motion responses at various drafts in regular waves and still water |
To sum up, during towing in still water, the structure showed a small motion response and a towing force mainly controlled by the size of the submerged area. Thus, the towing force of the structure improved with the increase in draft. Meanwhile, when towing in waves, the structure exhibited a large motion response under the action of waves, with the towing force influenced by the motion response of the structure. In shallow drafts, the structure exhibits poor stability and low height of sealed water inside the compartment. Thus, the compartments with roofs will be prone to leaking air when the sway angle is large, which seriously affects the safety of the towing process.
5.1.2 Influence of towing point height on regular wave towingFig.17 and Table 5 provide the motion response of the wellhead platform with a bucket foundation under various towing point heights in regular waves, and Fig.18 displays the statistical values of motion responses at various towing point heights in regular waves. The towing point exhibited a small influence on the structure motion response during towing in regular waves, and the pitch responses of the structure at the height of each towing point were relatively close, which deviates from the law of towing in still water. This finding was caused by the varied motion patterns of towing in still water and waves. During towing in still water, the structure showed a small sway angle. Notably, the quasistatic method was implemented for the analysis of the force and motion of the structure. At the towing point height of 10 cm, the towing point lay at the center of the flow impact surface, and almost little bending moments can be observed in the pitch direction, which resulted in a smaller pitch response of the structure compared with other towing point heights. During towing in waves, the motion response of the structure was greatly affected by wave action, and a large motion response of the structure was obtained. At this point, changes in the height of the towing point slightly influenced the motion of the structure. However, at the towing point height of 20 cm, the motion response, towing force, and air pressure were slightly higher than those of other towing points due to the increase in the submerged area caused by the relatively large forward tilt when the height of the towing point is 20 cm. In addition, the larger the towing point height, the larger the initial tension, which is due to the larger submerged area caused by the large forward tilt.

|
Fig. 17 Motion responses at various towing point heights in regular waves. |
|
|
Table 5 Motion responses at varied towing heights in regular waves and still water |

|
Fig. 18 Statistical values of motion at various towing point heights in regular waves. |
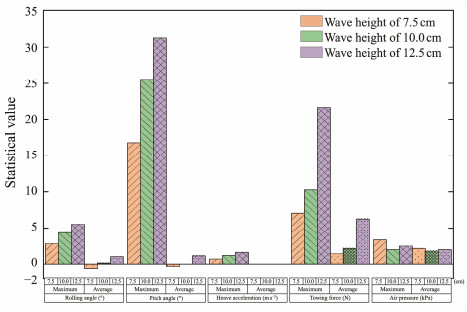
Fig.19 shows the motion response of the wellhead platform with bucket foundation under various wave heights during towing in regular waves, and Fig.20 reveals the statistical values of motion responses at various wave heights in regular waves. When the wave height increased from 7.5 cm to 12.5 cm, the average rolling angle increased from 0.6˚ to 1.0˚, and the standard deviation increased from 1.1˚ to 1.70˚. The average pitch and standard deviation increased from 0.34˚ to 1.14˚ and from 8.66˚ to 16.96˚, respectively. The average heave acceleration remained unchanged, and the standard deviation increased from 0.33 m s−2 to 0.68 m s−2. The average towing force and standard deviation increased from 1.46 N to 6.28 N and from 0.82 N to 4.43 N, respectively. The average pressure and standard deviation, respectively, increased from 1.79 kPa to 2.17 kPa and from 0.084 kPa to 0.32 kPa. Therefore, with the increase in wave height, the mean and amplitude of the pitch angle, towing force, and air pressure increased, and the amplitude of heave acceleration, whose average value remained unchanged, increased. The initial tension increased with the increase in wave height and was considerably larger than the tension during stable towing. Thus, large wave heights must be avoided during towing.
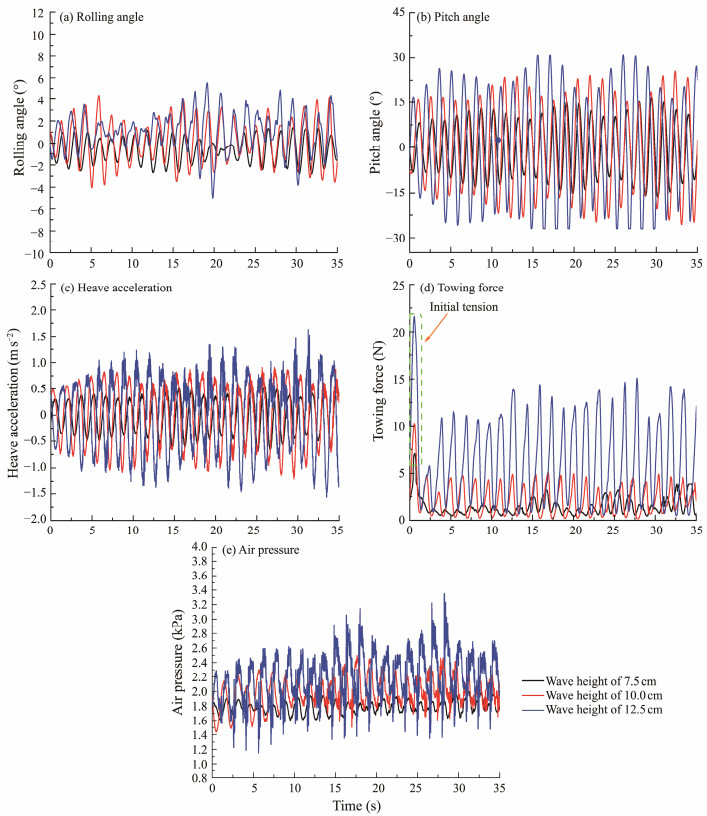
|
Fig. 19 Motion responses at various wave heights in regular waves. |
|
Fig. 20 Statistical values of motion at various wave heights in regular waves. |
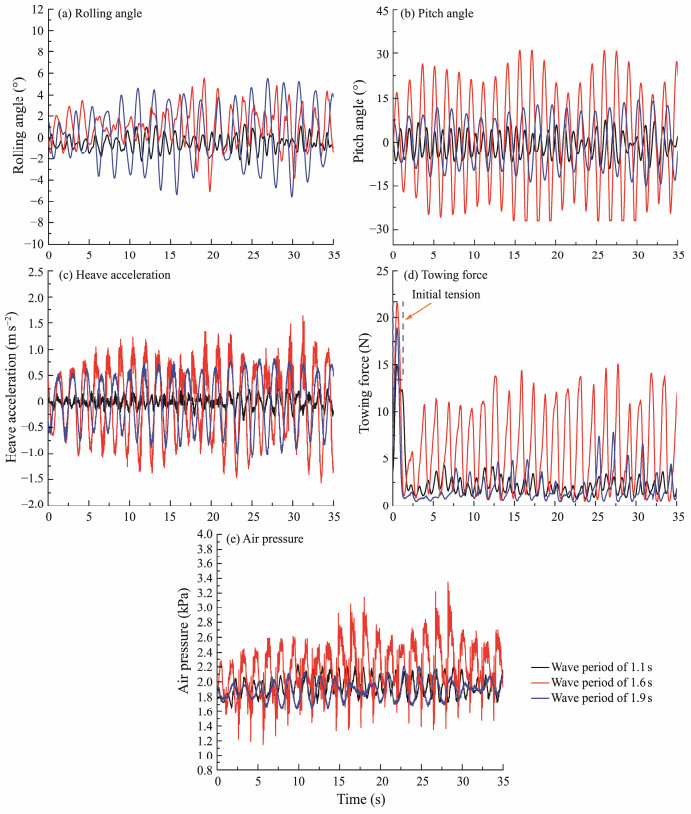
Fig.21 shows the motion response of the wellhead platform with a bucket foundation under various wave periods during towing in regular waves, and Fig.22 reveals the statistical motion responses at various wave periods in regular waves. In addition to the rolling response, the pitch, heave acceleration, towing force, and air pressure of the structure exhibited the largest response under a wave period of 1.6 s and were considerably higher than the motion response under other wave periods, and the rolling response was the largest under the wave period of 1.9 s. Based on the free attenuation test results, rolling, pitch, and heave have natural periods of 2.0, 1.45, and 1.4 s, respectively. The comparison showed the consistency between a wave period corresponding to the maximum response of structures and the natural period of the structure motion. The closer the wave period is to the natural period, the more intense the motion response of the structure becomes. Meanwhile, the towing force and pressure in the compartments were evidently affected by the wave period, and the response was the largest under a wave period of 1.6 s, which showed that the towing force and pressure were highly related to the pitch and heave of the structure. In addition, the simultaneous increase in the pitch and heave of the structure directly led to the increased fluctuation range of the towing force and interior air pressure. The initial tension was substantially larger than the tension during stable towing and sensitive to wave period. Thus, natural periods must be avoided during towing.
|
Fig. 21 Motion responses at various wave periods in regular waves. |

|
Fig. 22 Statistical motion at various wave periods in regular waves. |
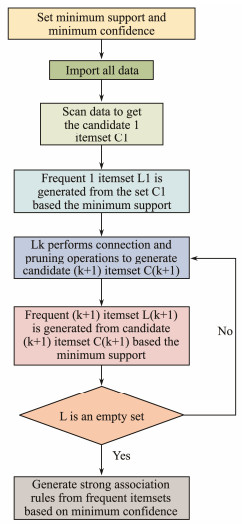
To better quantify and compare the relationships between various influencing factors and towing response, we used the classic association rule mining algorithm, Apriori algorithm, to analyze the effects of various factors on the towing response of the structure (Ding et al., 2022). The core concept of the Apriori algorithm stems from a recursive method based on the frequent item set theory, which uses a layer-by-layer search iterative procedure to mine all frequent item sets in the target database until the highest-order frequent item set is found. Finally, strong association rules were obtained through the calculation of the acquired frequent item sets. Fig.23 shows the algorithm flow chart.
|
Fig. 23 Apriori algorithm flow chart. |
In this part, the rolling and pitch angle, heave acceleration, and towing force, which pose the most concern during the towing process, were studied. Each influencing factor and its corresponding motion response can be considered as an item set ai:
| $ a_i=\left\{t_i, r_{i j}, p_{i j}, h_{i j}, f_{i j}\right\}, $ |
where ti refers to various influencing factors, including the different drafts, towing point heights, wave heights, and wave periods. rij, pij, hij, and fij, respectively, represent the rolling angle, pitch angle, heave acceleration, and towing force corresponding to the influencing factor ti at time j.
The Apriori algorithm mainly involve the concepts of support, confidence, and lift:
| $ \begin{gathered} \text { Support }(X \rightarrow Y)=\frac{\operatorname{count}(X, Y)}{\operatorname{count}(I)}, \\ \text { Confidence }(X \rightarrow Y)=\frac{\operatorname{count}(X, Y)}{\operatorname{count}(X)}, \\ \operatorname{Lift}(X \rightarrow Y)=\frac{P(Y / X)}{P(Y)}, \end{gathered} $ |
where count(X, Y) represents the number of simultaneous occurrences of items X and Y, and count(I) denotes the total number of items; P(Y/X) refers to the probability of occurrence of item Y in the item set containing the occurrence of item X, and P(Y) indicates the probability of occurrence of item Y.
In this paper, lift was used to determine the effects of various factors on towing motion characteristics. At the lift greater than 1, X has a lifting effect on Y; at the lift less than 1, X has an inhibitory effect on Y; when the lifting degree equals 1, then X is independent of Y.
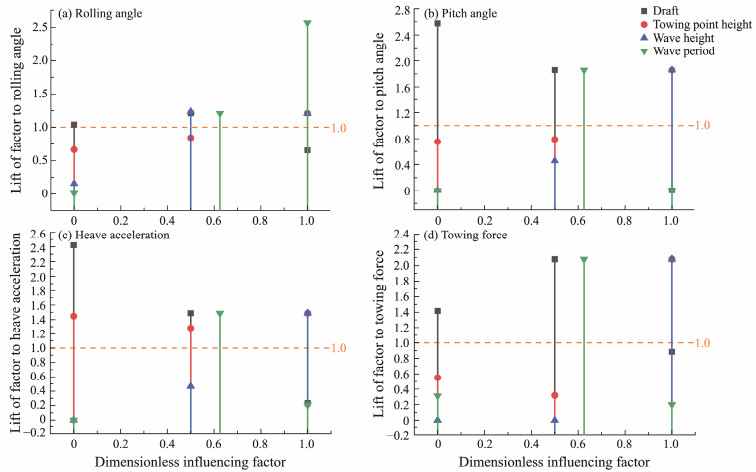
After various tests, the minimum support and confidence were both determined and set as 1% in the program. In consideration of the motion response of the standard group in waves (test condition 12) as the reference, 80% of the absolute values of a motion response were regarded as the large values of the corresponding motion response. The large values of rolling angle, pitch angle, heave acceleration, and towing force were 2.53˚, 23.13˚, 0.88 m s−2, and 10.63 N, respectively. The association rules between the influencing factor and {the absolute value of motion response > the large value} were established, and their corresponding lift, which represents the characterization value of the effect of the influencing factor on the motion response, is determined. Fig.24 shows the lift of each influencing factor on the motion response.
|
Fig. 24 Lift of each influence factor on the motion response. |
For the rolling angle of the structure, the influence of factors was inevident, except for the change in wave period. For the pitch angle, Lift(draft→pitch) decreased with the increase in the draft; that is, the greater the draft, the more evident the inhibition effect exerted on the pitch angle; the larger the wave height, the greater the Lift(wave height→pitch). Only when the wave period is close to the natural period of the structure can it exhibit a large lift to the pitch angle. The change in the towing point height showed no evident influence on the lift of the pitch angle. The variation in heave acceleration lift with various influencing factors is consistent with that of the pitch angle. For the towing force, the lift of the draft to the towing force first increased and then decreased with the increase in the draft, which deviates from the variation law presented in the maximum value of the time history curve. This finding demonstrates that although the maximum towing force at the draft of 15 cm was considerably greater than that of the other draft, on the whole, the amount of large-value data is less; that is, the large values of towing force are in the form of a pulse.
5.2 Towing Test in Irregular WaveTo simulate waves in a real sea state, we added three groups of towing tests in irregular waves for analysis. The selected significant wave height was 12.5 cm, and the wave periods were 1.1, 1.6, and 1.9 s. Fig.25 shows the towing test results for the irregular waves. The pitch, heave acceleration, towing force, and air pressure of the structure presented the largest response under the wave period of 1.6 s, and their values were substantially higher than the motion response under other wave periods. Meanwhile, the rolling response was the largest under the wave period of 1.9 s. The wave period corresponding to the maximum response was consistent with the natural period of the structure motion, which is the same as the variation law of the influence of wave periods on the structure motion response under regular waves. In addition, compared with that under regular waves, the motion response of the structure is consistent with the distribution of the wave curve, which indicates that the influence of waves on motion response becomes dominant when towing in waves.
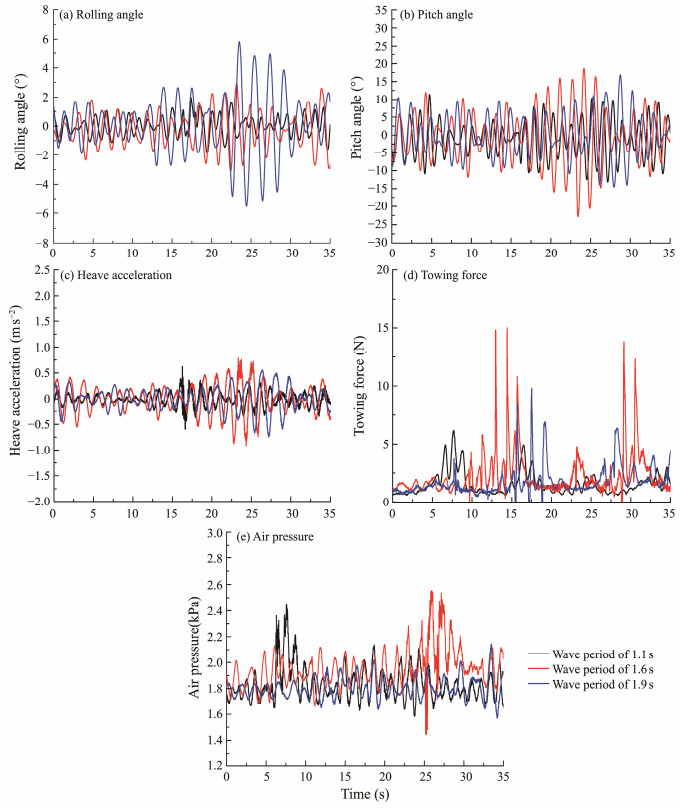
|
Fig. 25 Motion responses at various wave periods in irregular waves. |
For a demonstration of the application value of the structure in practical engineering, the test results in irregular waves were compared with industry standards. According to the relevant standards (China Classification Society, 2011), the motion standards shown in Table 6 can be accepted during towing.
|
|
Table 6 Default motion standards (China Classification Society, 2011) |
The studied wellhead platform conformed to mode condition 5, and the motion response must meet the following requirements: rolling angle < 30˚, pitch angle < 30˚, and heave acceleration < 0.2 g. Fig.25 shows that the motion response in irregular wave test conditions can reach target specifications.
The test results under irregular waves were compared to those under regular waves (Fig.26). The maximum value and standard deviation were selected for the analysis because the mean values of motion responses under various wave periods were the same. Compared with those in irregular waves, the pitch and heave responses in regular waves were more sensitive to the wave period because irregular waves contain numerous wave components of various periods, which weakened the amplification effect of single wave periods on motion response.

|
Fig. 26 Comparison of motion responses in irregular and regular waves. |
Based on the towing test of an integrated rounded rectangular wellhead platform with a bucket foundation, a comprehensive analysis of the towing stability of the structure was performed. The towing tests on the structure in still water and waves were carried out, and the effects of various factors (draft, towing point height, and wave parameters) on the towing process were investigated. The influences of various factors on the motion response were quantified and compared using the concept of lift in the Apriori algorithm. The following conclusions were obtained:
1) The motion mode of the structure during towing in still water varied from that during towing in waves, which was mainly reflected in the distribution of pitch angle and towing force. During towing in still water, the pitch angle and towing force of the structure fluctuated within a small range around a certain value, and the pitch angle of the structure during towing in waves fluctuated greatly around 0. Meanwhile, a pulse form oscillation of the towing force was observed. When towing in still water, the overall motion response and acceleration change of the structure were small. The force and motion of the structure can be analyzed via the quasistatic method. However, the overall motion response of the structure was large when towing in waves, and the wave action directly led to changes in structure acceleration. Therefore, the structure motion is consistent with that of the wave when towing in waves.
2) Given the different motion modes, the draft and height of the towing point exhibit various effects on the structure in still water and waves. One evident difference is: i) When towing in still water, with the increase in draft, the pitch angle first decreased and then increased, and the towing force gradually increased. When towing in waves, the pitch angle and towing force decreased with the increase in the draft. Thus, the draft should be appropriately increased in the actual towing process. ii) At the 10 cm towing point height during still water towing, the pitch response of the structure was considerably smaller than that of other towing point conditions. However, when towing in waves, the pitch angle of the structure was less sensitive to changes in the height of the towing point. At the towing point height of 20 cm, the pitch angle was slightly greater than that under other towing point conditions.
3) The association rules were mined using the Apriori algorithm, and the degrees of improvement of the influence factors on the motion response were obtained. With the increase in the draft, the lift of the draft on the towing force increased first and then decreased. This finding indicates that although the maximum towing force at the draft of 15 cm was notably greater than other draft conditions, the large-value data amount of the towing force was less, and large values were in the form of pulses.
4) The structure exhibited an increased motion response with the increase in wave height, and the wave period corresponding to the maximum response was consistent with the natural period of structure motion. The pitch and heave response presented weaker sensitivities to wave period in irregular waves than in regular waves.
AcknowledgementThe authors would like to acknowledge the support from the National Natural Science Foundation of China (No. 52171274).
Author Contributions
All authors contributed to the study conception and design. Material preparation and data collection were performed by Yu Bai. Data analysis and manuscript writing were performed by Jingyi Li. And Puyang Zhang, Conghuan Le and Hongyan Ding commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Data Availability
All data generated and analyzed during this study are included in this published article and its additional files.
Declarations
Ethics Approval and Consent to Participate
This article does not contain any studies with human participants or animals performed by any of the authors.
Consent for Publication
Informed consent for publication was obtained from all participants.
Conflict of Interests
The authors declare that they have no conflict of interests.
China Classification Society, 2011. GD 02-2012 Guidelines for Towage at Sea. China Classification Society: 30-31 (in Chinese). (  0) 0) |
China Commercial Industry Research Institute, 2020. Research report on market prospect and investment opportunities of China's offshore equipment industry (in Chinese).
(  0) 0) |
Chu, X. J., 2012. Study on the status of offshore oil storage technology and non-pollution oil storage technology underwater. Applied Mechanics & Materials, 110-116: 4151-4155. DOI:10.4028/www.scientific.net/AMM.110-116.4151 (  0) 0) |
Cui, W. T., 2014. The research on application of simple wellhead platform with suction pile in Weizhou Bay. Master thesis. Tianjin University.
(  0) 0) |
Deng, S., Liu, Y. L., Jiang, P. L., Zhu, S., Tao, L., and He, Y. F., 2019. Simulation and experimental study of deepwater subsea wellhead-shallow casing deflection considering system mass force. Ocean Engineering, 187: 106222. DOI:10.1016/j.oceaneng.2019.106222 (  0) 0) |
Ding, H. Y., Feng, Z. T., Zhang, P. Y., and Le, C. H., 2022. Integrated towing transportation technique for offshore wind turbine with composite bucket foundation. China Ocean Engineering, 36(1): 133-143. DOI:10.1007/s13344-022-0012-0 (  0) 0) |
Ding, H. Y., Liu, J. H., and Shen, K. L., 2008. Towing analysis of bucket foundation ocean platform based on multivariate statistics. Journal of Tianjin University, 7: 783-787. DOI:10.3969/j.issn.0493-2137.2008.07.004 (  0) 0) |
Ding, H. Y., Liu, X. Q., Zhang, P. Y., Diao, J. H., and Xu, F. F., 2012. Test research on impact of towing of ocean platform with four-bucket foundations. Journal of Tianjin University (Science and Technology), 45(1): 43-49 (in Chinese with English abstract). (  0) 0) |
Ding, H. Y., Shi, J. C., Zhang, P. Y., and Huang, X., 2016a. Analysis of effect of floating state of wind turbine group on wind turbine transport ship. Journal of Tianjin University (Science and Technology), 49(10): 1034-1040 (in Chinese with English abstract). (  0) 0) |
Ding, H. Y., Shi, J. C., Zhang, P. Y., Le, C. H., and Huang, X., 2016b. Analysis of wind turbine transport ship seakeeping performance during towing. Periodical of Ocean University of China, 46(12): 104-110 (in Chinese with English abstract). DOI:10.16441/j.cnki.hdxb.20150117 (  0) 0) |
Ding, H. Y., Zhao, X., Le, C. H., Zhang, P. Y., and Min, Q. L., 2019. Towing motion characteristics of composite bucket foundation for offshore wind turbines. Energies, 12(19): 3767. DOI:10.3390/en12193767 (  0) 0) |
Jouffray, J. B., Blasiak, R., Norstrm, A. V., Sterblom, H., and Nystrm, M., 2020. The blue acceleration: The trajectory of human expansion into the ocean – Science direct. One Earth, 2(1): 43-54. DOI:10.1016/j.oneear.2019.12.016 (  0) 0) |
Le, C. H., Ding, H. Y., Dong, G. H., and Zhang, P. Y., 2012. Model test and analysis of influence of trim angle on towing of platform with air cushion supported by bucket foundation. Journal of Huazhong University of Science and Technology (Natural Science Edition), 40(6): 86-89 (in Chinese with English abstract). DOI:10.13245/j.hust.2012.06.002 (  0) 0) |
Li, D. Q., and Cao, H. J., 2013. The application research for wellhead platform with suction pile marginal oil field development. China Offshore Platform, 28(4): 8-11 (in Chinese with English abstract). (  0) 0) |
Li, Y., Li, Y. L., Zhao, Z. M., Tang, Y. G., Li, H. R., Zhang, Y. J., et al., 2023. Dynamic responses of the cylindrical floating drilling production storage and offloading system with annular anti-motion structures under the survival sea scenario. Journal of Marine Science and Engineering, 11(1): 218. DOI:10.3390/jmse11010218 (  0) 0) |
Malde, K., Handegard, N. O., Eikvil, L., and Salberg, A. B., 2020. Machine intelligence and the data-driven future of marine science. ICES Journal of Marine Science, 77(4): 1274-1285. DOI:10.1093/icesjms/fsz057 (  0) 0) |
Min, Q. L., 2018. Analysis of stability and towing motion characteristics of composite bucket foundation. Master thesis. Tianjin University.
(  0) 0) |
Qiu, N., Liu, X. Q., Liu, Z. W., Li, Y. W., Chang, Y. J., Chen, G. M., et al., 2022. Dynamic stability evaluation of subsea wellhead based on fully coupled model. Ocean Engineering, 8: 257. DOI:10.1016/j.oceaneng.2022.111720 (  0) 0) |
Ruschel, A., Dantas, C. M. S., Sousa, F. J. M. D., Simo, M. L., and Oliveira, F. L., 2021. Wellhead fatigue analysis considering the effect of wind-sea and swell waves by using Univariate Dimension Reduction Method. Journal of Petroleum Science and Engineering, 206: 108989. DOI:10.1016/j.petrol.2021.108989 (  0) 0) |
Shan, Y. W., Liu, J. C., Zhou, G. H., Li, X. J., and Zhang, Y. X., 2011. Preliminary discussion on offshore installation and construction of CFD18-1/JZ9-3W bucket foundation platform in marginal oilfield. Engineering Construction Department of CNOOC: 5pp (in Chinese). (  0) 0) |
Wang, S. Y., 2008. Application study of bucket foundation platform in the developing marginal oilfield in Bohai Sea. Master thesis. Dalian University of Technology.
(  0) 0) |
Wang, Y. B., and Gao, D. L., 2021. On the static mechanics of the tubular system during installation of the surface casing in deepwater drilling. Applied Ocean Research, 110(1): 102599. DOI:10.1016/j.apor.2021.102599 (  0) 0) |
Wang, Y. B., and Gao, D. L., 2022. Study on the marine environment limiting conditions of deepwater drilling for natural gas hydrate. Applied Energy, 312(8): 118802. (  0) 0) |
Yan, C. J., Wang, H. J., Guo, Y. H., Wang, Z., and Liu, X., 2021. Laboratory study of integrated wet-towing of a triple-bucket jacket foundation for far-offshore applications. Journal of Marine Science and Engineering, 9(11): 1152. DOI:10.3390/jmse9111152 (  0) 0) |
Yu, H., Liu, Q., Sun, Y. Z., Guo, X. F., and Yu, G. X., 2020. Discussion on development pathway of offshore oil and gas fields from global low-carbon perspective. Modern Chemical Industry, 40(5): 1-3, 9 (in Chinese with English abstract). DOI:10.16606/j.cnki.issn0253-4320.2020.05.001 (  0) 0) |
Yu, Y., Pei, H. L., and Xu, C. Z., 2017. Parameter identification of JONSWAP spectrum acquired by airborne lidar. Journal of Ocean University of China, 16(6): 998-1002. DOI:10.1007/s11802-017-3271-2 (  0) 0) |
Zhang, M. H., Yang, J., Wang, Y. M., Zhou, Y. S., Yang, Y. X., and Long, Y., 2022. Study on the static mechanics and control method of the tubular system during subsea wellhead construction in deep water. Ocean Engineering, 266: 113108. DOI:10.1016/j.oceaneng.2022.113108 (  0) 0) |
Zhang, P. Y., Han, Y. Q., Ding, H. Y., and Zhang, S. Y., 2015. Field experiments on wet tows of an integrated transportation and installation vessel with two bucket foundations for offshore wind turbines. Ocean Engineering, 108: 769-777. DOI:10.1016/j.oceaneng.2015.09.001 (  0) 0) |
Zhang, P. Y., Liang, D. S., Ding, H. Y., Le, C. H., and Zhao, X., 2019. Floating state of a one-step integrated transportation vessel with two composite bucket foundations and offshore wind turbines. Journal of Marine Science and Engineering, 7(8): 263. DOI:10.3390/jmse7080263 (  0) 0) |
Zhang, P. Y., Shi, J. C., Ding, H. Y., and Huang, X., 2014. Floating analysis of composite bucket foundation for offshore wind turbine. Acta Energiae Solaris Sinica, 35(11): 2313-2319 (in Chinese with English abstract). (  0) 0) |
Zhao, P. F., Wang, Q. R., and Chen, F., 2020. Classification of reserves and contingent resources of offshore oil and gas resources. Marine Geology Frontiers, 36(10): 68-75 (in Chinese with English abstract). DOI:10.16028/j.1009-2722.2020.113 (  0) 0) |
 2025, Vol. 24
2025, Vol. 24


