2) Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266237, China;
3) Shengli Branch, Sinopec Geophysical Company Limited, Dongying 257086, China
In recent years, there has been a growing emphasis on cost reduction and efficiency enhancement in marine seismic exploration, thus promoting the development of marine seismic blended acquisition technology. Unlike traditional acquisition methods, this approach facilitates the simultaneous activation of multiple sources within the same timeframe, thus enabling multishot reception while enhancing exploration efficiency. However, the concurrent activation of multiple sources over a short duration results in blended seismic data, which can affect subsequent processing. Consequently, de-blending the received multishot data into single-shot data has become a pivotal challenge in this field. At the moment, there are two primary conventional methods for de-blending blended data: treating adjacent source interference as noise and using denoising techniques or inversion methods.
The blended data denoising method was originally proposed by Vaage (2005). In the common receiver domain, the direct wave and reflected wave of the main source have strong coherence, but the direct and reflected waves of the auxiliary source are randomly distributed, which can be used to de-blend the blended data. Following this idea, Mahdad et al. (2011) converted blended data into noiseunrelated domains, applied filtering techniques to suppress noise and employed thresholds to gradually eliminate residual noise. They also used iterative thresholds to recover more signals. Maraschini et al. (2012) used an iterative de-blending method based on reduced-rank filtering, effectively de-blending blended seismic data even in cases of low signal-to-noise ratios (SNR). Ibrahim and Sacchi (2014) employed the Radon transform to treat the auxiliary source in the common receiver domain as noise, while Chen et al. (2015) used a regularization framework to denoise seismic blended data. Gong et al. (2016) processed blended data in different domains in accordance with a specific process. Zhou et al. (2016) used the adaptive median filtering method for blended noise suppression and recommended the use of different adaptive filtering windows in various iteration stages. Zu et al. (2016a) employed periodic source coding to suppress blended noise, while Zhang et al. (2017) proposed a trilateral filtering method in their comparative analysis with median filtering. Their experiments demonstrated that, particularly when the random time delay is shorter, the trilateral filtering method is able to preserve more details. Guo et al. (2019) proposed a noise suppression criterion with enhanced stability and minimal disruption to effective signals, in which they used the multi-vector median filtering method.
Bahia et al. (2020) achieved blended data separation through iterative Fourier thresholding, successfully removing a significant portion of blended noise with fewer iterations. In a subsequent study, Bahia et al. (2021) employed regularization in blended data separation and evaluated its performance across various denoising operators. Amin et al. (2021) proposed a blended noise suppression method based on prior information, while Chen et al. (2022) proposed a frequency structure weighted threshold denoising method for de-blending blended data. Zhang et al. (2023a) proposed a blended noise suppression process in multiple domains.
The inversion method generally regards de-blending as an underdetermined problem and solves it by adding constraints. Different regularization constraints correspond to varying solutions. For example, Abma et al. (2010) proposed a high-quality de-blending strategy using a sparse inversion method, in which they leveraged the predictability of adjacent source interference as an additional constraint to achieve effective signal separation. Bulcão et al. (2011) used full waveform inversion to de-blend, demonstrating the recovery of almost all features in the original data even with a low SNR. Zhang et al. (2013) used the sparse inversion algorithm on Gulf of Mexico field data, resulting in a significant de-blending effect post-inversion. Han et al. (2013) proposed a de-blending method based on sparse inversion, combining multilevel median filtering with the curvelet threshold iterative denoising algorithm. Zu et al. (2016b) used the regular sampling de-blending method to irregular sampling data, in which they introduced the Mask operator for interpolation and separation processing, effectively transforming the de-blending problem into an iterative shrinkage threshold problem.
Meanwhile, Tsingas et al. (2020) proposed a reducedrank de-blending algorithm, thereby enhancing the resolution and continuity of seismic data. Chen et al. (2021) proposed a system featuring logical coordinate dynamic mapping processing to efficiently identify multiple blended noises, thereby demonstrating favorable results with field OBN data. Jiang et al. (2021) proposed self-interference separation technology for de-blending, proving that excitation time influenced blended noise suppression. To de-blend the blended data caused by borehole-gun alternating excitation, Xu et al. (2023) proposed a method based on the generalized synchrosqueezed curvelet transform and least squares matched filtering. Zhang et al. (2023a) proposed using the curvelet transform to de-blend blended data of different scales and directions, thus resolving the issue of the inapplicability of the inversion algorithm in borehole explosive source data separation.
In the de-blending of marine seismic blended data, traditional denoising methods often suffer from issues such as information loss, dependency on parameters, and limited efficacy. Similarly, inversion methods have limitations, such as instability, heavy reliance on initial models, and the nonuniqueness of solutions to the inverse problem. With advancements in computer hardware, deep learning (DL) deblending methods have experienced rapid development. For example, Baardman and Tsingas (2019) conducted experiments on the classification and recognition of blended noise within synthetic seismic data, demonstrating the potential of DL for de-blending. Slang et al. (2019) proposed a convolutional neural network (CNN) for the de-blending of marine blended data in the common receiver domain. Richardson and Feller (2019) integrated Unet with residual neural networks, thus addressing the challenge of de-blending in the common offset domain. Sun et al. (2020) provided evidence that normalization techniques can enhance DL performance, noting that the effectiveness of de-blending significantly depends on the SNR in seismic data. To deblend seismic data, Zu et al. (2020) proposed a net-work consisting of convolutional and deconvolutional modules.
Matharu et al. (2020) used a deep residual neural network for de-blending ocean bottom cable (OBC) data, concluding that the residual connection module in the Dn-CNN architecture is particularly efficacious for signal recovery. Tong et al. (2021) used CNN for the de-blending of marine towed cable seismic data. Nakayama and Blacquière (2021) proposed a comprehensive machine learning approach that concurrently addressed de-blending, low-frequency extrapolation, and data reconstruction. Wang et al. (2021) proposed a self-supervised learning method tailored for de-blending, thereby presenting a flexible algorithm that balances speed and precision in denoising tasks. Zhang et al. (2022) enhanced the DnCNN model and the Vision Transformer model for improved performance in deblending tasks.
The present paper introduces the Uformer network (Wang et al., 2022) capable of synergizing the transformer framework with the encoding-decoding concept of Unet. The Uformer as a whole is a U-shaped structure featuring a transformer instead of convolution to achieve encoding and decoding. To enhance Uformer's ability to capture local context, we added depthwise convolution to the feedforward network and used nonoverlapping window multihead attention instead of traditional multihead attention to reduce the amount of calculation. Regarding the loss function, we employed a novel approach by combining SSIM loss with L1 loss. Comparative evaluations reveal that the Uformer outperforms CNN and traditional denoising methods in the de-blending of blended seismic data in the common shot domain.
2 De-Blending Principle and Uformer Architecture 2.1 De-Blending PrincipleBlended source acquisition is characterized by the concurrent excitation of multiple sources within a brief period of time. This practice results in the superposition of wave fields from adjacent sources, consequently generating interference. Its expression is shown as follows:
| $ y = s + n, $ | (1) |
where s is the unblended data, n is the noise of the adjacent source, and y is the blended data.
2.2 Uformer ArchitectureAs shown in Fig.1, Uformer features a U-shaped hierarchical structure, wherein a skip connection is established between the encoder and the decoder. Furthermore, a shortcircuit link is incorporated between the network input and output.

|
Fig. 1 Overall structure of the Uformer. |
Firstly, the seismic data were fed into the input layer, which included the LeakyReLU activation function and the 3 × 3 convolution. This layer was used to extract the features of the input. Subsequently, the feature map progresses through the encoder, each consisting of two Transformer encoder blocks. Here, the Transformer encoder and decoder blocks share an identical design, details of which will be presented in the subsequent section. Downsampling within the network was accomplished through the 4 × 4 convolutions with a stride of 2, while upsampling was completed through the 2 × 2 deconvolutions, also with a stride of 2. This particular process concluded in the output layer, in which the 3 × 3 convolution was used to restore the data to its original input size. The tanh function was used to activate the data before output because data normalization occurs within the range of [−1, 1] during preprocessing.
2.3 Attention Mechanism and Multihead Attention MechanismThe calculation of the self-attention mechanism is an addressing process. Given a query vector Q (query), the mechanism computes the similarity between a key vector K (key) and Q. This similarity is then applied to a value vector V to obtain a weighted value. The process can be detailed as follows:
Assume X = [x1, ···, xi, ···, xn] as the input. Each element x1, ···, xi, ···, xn was first encoded to a corresponding a1, ai, and an. Then, these encoded elements were then multiplied by learnable matrices Wa, Wk, and Wv to obtain qa, qk, and qv, respectively. Subsequently, each q was multiplied by all k values to calculate their similarities. After scaling these similarities, a weight matrix was derived using the Softmax function. This weight matrix was then multiplied by the respective v values and aggregated to produce the outputs y1, yi, and yn. Its expression is shown as follows:
| $ \operatorname{Attention}(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})=\operatorname{Softmax}\left(\frac{\boldsymbol{Q} \boldsymbol{K}^{\mathrm{T}}}{\sqrt{d_k}}\right) \boldsymbol{V}, $ | (2) |
where Q, K, and V are involved in the calculation in the form of vectors, and
Fig.2 presents the calculation process of the multihead attention mechanism. This attention mechanism calculates qi, ki and vi, and then divides each qi, ki and vi into [qi, 1, ···, qi, h], [ki, 1, ···, ki, h], and [vi, 1, ···, vi, h] based on the number h of heads, after which it combines them into [qi, 1, ki, 1, vi, 1], ···, [qi, h, ki, h, vi, h]. The self-attention of [qi, 1, ki, 1, vi, 1], ···, [qi, h, ki, h, vi, h] is calculated and concatenated, so that the multiscale features are obtained. The calculation of the multihead attention mechanism is as follows:
| $ \operatorname{multihead}(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})=\operatorname{Concat}\left(\operatorname{head}_1, \cdots, \operatorname{head}_h\right) \boldsymbol{W}^0, $ | (3) |
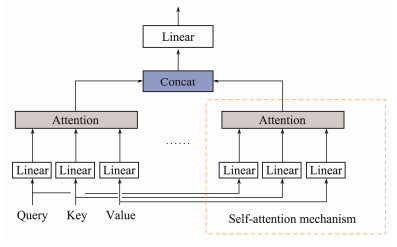
|
Fig. 2 Multihead attention mechanism. |
where W0 is the weight matrix. In addition, headi is calculated as follows:
| $ \operatorname{head}_i=\operatorname{Attention}\left(\boldsymbol{Q} \boldsymbol{W}_i^Q, \boldsymbol{K} \boldsymbol{W}_i^K, \boldsymbol{V} \boldsymbol{W}_i^V\right) . $ | (4) |
Fig.1b shows the computational process of the Transformer encoder (decoder) block. Here, 'layer norm' refers to the layer normalization process. The W-MSA, or the nonoverlapping window multihead attention mechanism, plays a crucial role in reducing the amount of calculation. The principle of W-MSA involves partitioning the input X into n windows, each of an M × M dimension. These two-dimensional (2D) M × M data windows were then flattened into one-dimensional (1D) vectors with lengths of M2. Attention calculations were independently performed on each of these 1D vectors. Subsequently, the results were combined to form the final output. The calculation is as follows:
| $ {\hat X_k} = \{ Y_k^1, Y_k^2, \cdot \cdot \cdot, Y_k^N\}, $ | (5) |
where
| $Y_k^i=\operatorname{Attention}\left(X^i \boldsymbol{W}_k^Q, X^i \boldsymbol{W}_k^K, X^i \boldsymbol{W}_k^V\right), $ | (6) |
where Xi is the different partition windows.
Fig.1c shows the locally enhanced feedforward module, a component that is designed to augment the network's capability to capture contextual information. The process begins with the input data passing through a linear projection layer, which increases the data dimension. Subsequently, these 1D data were expanded into a 2D format. Next, depthwise convolution was employed to extract data features, specifically emphasizing local characteristics. The process continues with a 'Flatten' operation, which converts the data back to a 1D. Another linear projection layer was then used to restore the data to its original input dimension. The linear layer was implemented through the 1 × 1 convolution, with the GELU activation function applied after each 1 × 1 convolution and depthwise convolution. The loss function combined L1 and SSIM loss (Zhao et al., 2017).
3 Numerical Simulation and Training Strategy 3.1 Dataset Preparation and Training DetailsTo evaluate Uformer's performance in comparison with CNN and traditional denoising methods, it was trained and tested using synthetic and field data, respectively. The hyperparameters were set as follows: a batch size of 16 was established, an initial learning rate was set at 2e −4, and the Adam W optimization algorithm was employed. Furthermore, an exponential decay strategy for the learning rate was adopted, with the decay rate set at 0.98.
The CNN architecture was designed with a total of 17 layers. The initial layer, serving as the input layer, executes the 3 × 3 convolution followed by the parametric rectified linear unit (PReLU) activation function. The terminal layer, functioning as the output layer, also employs the 3 × 3 convolution. Interposed between these two layers are 15 identical modules, each comprising the 3 × 3 convolution operation succeeded by batch normalization and a PReLU activation function. In comparison, the traditional denoising method uses the WildAmpAtten module, which is a component of the Geoeast seismic data processing commercial software. The traditional denoising method requires domain conversion for de-blending. Unlike this approach, the network training of CNN and Uformer was executed directly in the common shot domain.
Relative to the CNN, the Uformer possesses a larger number of parameters. This increase in parameters is chiefly attributable to its attention mechanism, which, despite its powerful nature, tends to exhibit slower computational speeds compared to convolution-based computations. In terms of network depth, our experiments indicated that a 4-layer configuration in the Uformer is optimal for deblending. It was observed that further increment in the depth of the network does not substantially improve the denoising results.
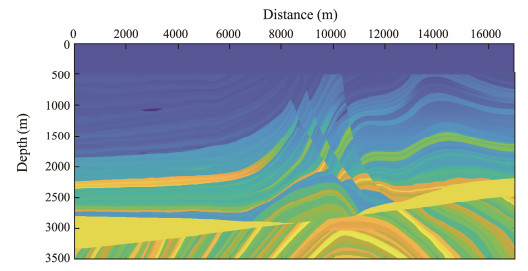
3.2 Synthetic Data TestingIn this study, the Marmousi velocity model (Fig.3) was used. The synthetic data were obtained by using the acoustic wave equation. The width of the model was set at 17000 m, the depth was 3500 m, the grid number of the velocity model was 700 × 2720, and the grid size was 6.25 m × 5 m. The shot point was placed at sea level; in particular, the horizontal direction was shot at 12.5 intervals, and a total of 1280 shots were set. A total of 256 detection points were arranged at a distance of 450 m from sea level, while the horizontal direction was arranged at an interval of 66 m. We used the Ricker wavelet excitation with a sampling rate of 4 ms and a recording time of 5.12 s. The blending between different shot data was performed based on the random time delay of 1 ± 0.6 s. The 1 and 641 shots were blended first, followed by the 2 and 642 shots were blended afterward. We obtained 6400 samples of 256 × 256, of which 4480 samples (70%) were selected as the training set, 640 samples (10%) were selected as the validation set, and 1280 samples (20%) were selected as the test set.
|
Fig. 3 Marmousi velocity model. |
Fig.4 shows the common shot domain data, thereby illustrating the characteristics of the primary shot and adjacent source data. Notably, both exhibit a strong correlation. Fig.5 shows the de-blending results achieved using the traditional method. As shown in the results, while this method effectively suppresses the blended noise, it simultaneously causes noticeable damage to the reflected waves of the effective signal. Fig.6 shows the de-blending results obtained through CNN. In this case, CNN struggles to adequately suppress blended noise in the common shot domain, thus generating abnormal energy at the top of the effective signal. Fig.7 shows the de-blending results of the Uformer network. As can be seen, the Uformer demonstrates a robust capability to suppress blended noise, thus causing less damage to the effective signal than the traditional method and CNN.

|
Fig. 4 (a), unblended data; (b), blended data. |

|
Fig. 5 (a), traditional de-blending results; (b), de-blending error. |

|
Fig. 6 (a), CNN de-blending results; (b), de-blending error. |

|
Fig. 7 (a), Uformer de-blending results; (b), de-blending error. |
Fig.8 shows the comparison of single trace de-blending results. Specifically, the comparison was conducted on trace 65, an area in which the blended noise overlapped with the effective signal. Notably, the segment before 3 s remains unaffected by the blended noise, whereas the segment after 3 s is affected by the blended noise. Among the evaluated methods, Uformer demonstrates the most effective performance in safeguarding the integrity of the effective signal while simultaneously suppressing blended noise.

|
Fig. 8 Comparison of single trace de-blending results. (a), traditional method; (b), CNN; (c), Uformer. |
For the purpose of quantitative analysis, we introduced three metrics: peak signal-to-noise ratio (PSNR), SNR, and structural similarity index (SSIM) to assess the de-blending efficacy of the three methods. The corresponding results are presented in Table 1. The corresponding calculations are presented as follows:
| $ \left\{\begin{array}{l} M S E=\frac{\left\|y-y_0\right\|_2^2}{N} \\ P S N R=10 \lg \frac{\max \left(y^2\right)}{M S E} \end{array},\right., $ | (7) |
| $ SNR = 20\lg \left({\frac{{{{\left\| y \right\|}_2}}}{{{{\left\| {y - {y_0}} \right\|}_2}}}} \right), $ | (8) |
| $ SSIM = \frac{{(2{\mu _y}{\mu _{{y_0}}} + {C_1})(2{\sigma _{y{y_0}}} + {C_2})}}{{(\mu _y^2 + \mu _{{y_0}}^2 + {C_1})(\sigma _y^2 + \sigma _{{y_0}}^2 + {C_2})}}, $ | (9) |
|
|
Table 1 Comparison of the PSNR, SNR, and SSIM values of the three methods investigated in this study |
where y is the clean data; y0 is the network output data; N is the number of seismic data sampling points; μy and
The following field data came from the OBC production data in a shallow sea area of the Shengli Oilfield. The observation system has 16 receiver lines and 4 shot lines, while the number of receiving channels is 5120. In addition, track, line, source, and source row intervals were set at 25, 200, 50, and 100 m, respectively. The source was an air gun, and the sinking depth was 3 – 5 m. The depth of seawater had a range of 4 – 18 m, the recording length was 2.5 s, and the sampling rate was 2 ms. The 318 shot data were extracted for testing, after which the data were blended by dual-source alternating excitation. The random time delay of ± 1 s was used for blending between different sources. After slicing the data, 10000 samples were selected for training and testing, 7000 samples (70%) were selected as the training set, 1000 samples (10%) were selected as the validation set, and 2000 samples (20%) were selected as the test set.
Fig.9 shows the common shot domain data, while Fig.10 shows the de-blending results achieved using the traditional method. Although this method effectively suppresses most of the blended noise, it leaves behind residual noise, which is particularly noticeable outside the first arrival of the effective signal. Fig.11 shows the de-blending results of the CNN, indicating that it is less effective in suppressing blended noise. Fig.12 shows the de-blending results of the U-former, which exhibits superior performance in suppressing blended noise, thus resulting in a significantly lower residue of noise than the traditional method.

|
Fig. 9 (a), unblended data; (b), blended data. |

|
Fig. 10 (a), traditional de-blending results; (b), de-blending error. |

|
Fig. 11 (a), CNN de-blending results; (b), de-blending error. |

|
Fig. 12 (a), Uformer de-blending results; (b), de-blending error. |
Fig.13 is the comparison of single trace (trace 144) deblending results, while Table 2 shows the comparison of single trace de-blending results. As can be seen, the deblending data of Uformer is closest to the unblended data, similar to the synthetic data.

|
Fig. 13 Comparison of single trace de-blending results: (a), traditional method; (b), CNN; (c), Uformer. |
|
|
Table 2 Comparison of the PSNR, SNR, and SSIM values of the three methods investigated in this study |
Next, we selected marine towed cable seismic data for conducting blended noise suppression tests in the common shot domain, enabling us to further validate the adaptability of the Uformer for marine seismic data. The data were sourced from the towed cable seismic dataset provided by the Society of Exploration Geophysicists (SEG). For this experiment, two ships were aligned to travel in the same direction. The survey setup included 1001 shot points oriented east-west. Additionally, there were 120 detection points, with a sampling interval of 4 ms. The offset distance was set at 25 m, with a common mid-point interval of 12.5 m. The water depth in the study area was approximately 350 m.
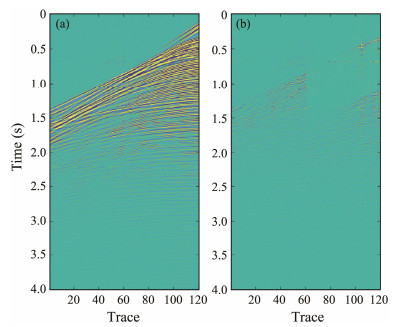
Fig.14 shows the marine towed cable seismic data, while Fig.15 shows the de-blending results obtained using the traditional method. This method, however, exhibits limitations in effectively suppressing large-scale blended noise within the effective signal. Fig.16 shows the de-blending results of CNN, demonstrating that it struggles to adequately suppress blended noise in the common shot domain. Fig.17 shows the de-blending results achieved with the Uformer. In particular, the Uformer network is successful in effectively suppressing blended noise, although it does introduce some alterations to the effective signal. Notably, these alterations manifest as changes in amplitude, while the overall continuity and shape of the effective wave event are preserved.

|
Fig. 14 (a), Unblended data; (b), blended data. |

|
Fig. 15 (a), traditional de-blending results; (b), de-blending error. |

|
Fig. 16 (a), CNN de-blending results; (b), de-blending error. |
|
Fig. 17 (a), Uformer de-blending results; (b), de-blending error. |
In this study, we introduced the Uformer network, an innovative architecture designed specifically for the deblending of seismic blended data. Uformer integrates the encoding-decoding concept of the Unet network with the architecture of the Transformer network. A notable advancement offered by the Uformer is its capability to directly suppress blended noise in the common shot domain, thus diverging from conventional denoising methods that typically necessitate data conversion to the noise-incoherent domain. Comparative analysis further reveals that, in the context of de-blending blended data within the common shot domain, the Uformer outperforms traditional methods and CNN in terms of minimizing noise residues and mitigating damage to the effective signal.
5.2 OutlookDespite the Uformer's efficacy in suppressing blended noise, it has been observed that the network can inflict some degree of damage to the effective signal during the denoising process. Thus, future studies could focus on enhancing the dataset construction and optimizing the network structure to minimize the impact on the effective signal during de-blending.
AcknowledgementsThis study is supported by the National Natural Science Foundation of China (Research on Dynamic Location of Receiving Points and Wave Field Separation Technology Based on Deep Learning in OBN Seismic Exploration, No. 42074140), the Sinopec Geophysical Corporation, Project of OBC/OBN Seismic Data Wave Field Characteristics Analysis and Ghost Wave Suppression (No. SGC-2022-06). Thanks are to Geoeast software support provided by BGP.
Author Contributions
Shiyu Wang: methodology, writing – original draft, writing – review and editing. Siyou Tong: investigation, resources, supervision, writing – review and editing. Jingang Wang: formal analysis, investigation, writing – review and editing. Hao Wei: formal analysis. Shuaijia Heng: formal analysis. Xiugang Xu: supervision. Dekuan Yang: data curation. Xu Zhang: data curation. Shurong Wang: data curation. Yuxing Li: data curation.
Data Availability
The data and references presented in this study are available from the corresponding author upon reasonable request.
Declarations
Ethics Approval and Consent to Participate
This article does not contain any studies with human participants or animals performed by any of the authors.
Consent for Publication
Informed consent for publication was obtained from all participants.
Conflict of Interests
The authors declare that they have no conflict of interests.
Abma, R. L., Manning, T., Tanis, M., Yu, J., and Foster, M., 2010. High quality separation of simultaneous sources by sparse inversion. 72nd EAGE Conference and Exhibition Incorporating SPE EUROPEC 2010. Barcelona, cp-161-00019.
(  0) 0) |
Amin, Y. I. K., Kumar, R., Mahdad, A., Bilsby, P., Narayan, A., Brouwer, W. G., et al., 2021. Robust multistage separation of simultaneous sources using priors: Challenges and strategies. First International Meeting for Applied Geoscience & Energy. Denver, SEG-2021-3583879.
(  0) 0) |
Baardman, R., and Tsingas, C., 2019. Classification and suppression of blending noise using convolutional neural networks. SPE Middle East Oil and Gas Show and Conference. Manama, SPE-194731-MS.
(  0) 0) |
Bahia, B., Lin, R., and Sacchi, M. D., 2020. Iterative deblending with robust Fourier thresholding. SEG Technical Program Expanded Abstracts 2020. Society of Exploration Geophysicists, 3279-3283, DOI: 10.1190/SEGAM2020-3425671.1.
(  0) 0) |
Bahia, B., Lin, R., and Sacchi, M., 2021. Regularization by denoising for simultaneous source separation. Geophysics, 86(6): P69-P83. DOI:10.1190/geo2021-0068.1 (  0) 0) |
Bulcão, A., Filho, D. M. S., Alves, G. C., Santos, L. A., Moreira, T. D. V., van den Berg, P., et al., 2011. Application of blended seismic data in full waveform inversion. 2011 SEG Annual Meeting. San Antonio, SEG-2011-2649.
(  0) 0) |
Chen, S., Cao, S., and Sun, Y., 2022. Deblending based on the frequency-structure weighted threshold: The case of the slopeconstrained f-k transform. Geophysics, 87(2): V131-V141. DOI:10.1190/geo2021-0095.1 (  0) 0) |
Chen, Y., Jin, Z., Gan, S., Yang, W., and Xiang, K., 2015. Deblending using a combined PNMO-MF-FK coherency filter. 2015 SEG Annual Meeting. New Orleans, SEG-2015-5715988.
(  0) 0) |
Chen, Y. P., Zhang, H. J., Liu Y., Zhao, M., Song, J. W., and Qi, Q. L., 2021. Deblending massive OBN data acquired by efficient and blended shooting method. Oil Geophysical Prospecting, 56(1): 86-91 (in Chinese with English abstract). (  0) 0) |
Gong, T., Xie, L., Wang, Y., Piao, R., and Guo, J., 2016. A processing workflow for blended OBC acquisition data. SPG/SEG 2016 International Geophysical Conference. Beijing, 20-22.
(  0) 0) |
Guo, J. H., Cheng, J. W., Chen, Z. R., Yang, B., and Yan, H., 2019. Seismic data separation of simultaneous source based on an improved iterative denoising method. Geophysical and Geochemical Exploration, 43(5): 1054-1063 (in Chinese with English abstract). (  0) 0) |
Han, L. G., Tan, C. Q., Lyu, Q. T., Zhang, Y. H., and Gong, X. B., 2013. Separation of multi-source blended seismic acquisition data by iterative denoising. Chinese Journal of Geophysics, 56(7): 2402-2412 (in Chinese with English abstract). (  0) 0) |
Ibrahim, A., and Sacchi, M. D., 2014. Simultaneous source separation using a robust Radon transform. Geophysics, 79(1): V1-V11. DOI:10.1190/geo2013-0168.1 (  0) 0) |
Jiang, T., Jiang, Y., Latchman, J., Cvetković, M., and Saunders, M., 2021. Deblending of single-source self-interference in a deep-water marine 2D survey. First International Meeting for Applied Geoscience & Energy. Denver, 2605-2609.
(  0) 0) |
Mahdad, A., Doulgeris, P., and Blacquiere, G., 2011. Separation of blended data by iterative estimation and subtraction of blending interference noise. Geophysics, 76(3): Q9-Q17. DOI:10.1190/1.3556597 (  0) 0) |
Maraschini, M., Dyer, R., Stevens, K., Bird, D., and King, S., 2012. An iterative SVD method for deblending: Theory and examples. 2012 SEG Annual Meeting. Las Vegas, SEG-2012-0675.
(  0) 0) |
Matharu, G., Gao, W., Lin, R., Guo, Y., Park, M., and Sacchi, M. D., 2020. Simultaneous source deblending using a deep residual network. SEG 2019 Workshop: Mathematical Geophysics: Traditional vs Learning. Beijing, 13-16.
(  0) 0) |
Nakayama, S., and Blacquière, G., 2021. Machine-learning-based data recovery and its contribution to seismic acquisition: Simultaneous application of deblending, trace reconstruction, and low-frequency extrapolation. Geophysics, 86(2): P13-P24. DOI:10.1190/geo2020-0303.1 (  0) 0) |
Richardson, A., and Feller, C., 2019. Seismic data denoising and deblending using deep learning. ArXiv: 10.48550/arXiv. 1907.01497.
(  0) 0) |
Slang, S., Sun, J., Elboth, T., McDonald, S., and Gelius, L. J., 2019. Using convolutional neural networks for denoising and deblending of marine seismic data. 81st EAGE Conference and Exhibition 2019, 2019: 1-5. (  0) 0) |
Sun, J., Slang, S., Elboth, T., Greiner, T. L., McDonald, S., and Gelius, L. J., 2020. A convolutional neural network approach to deblending seismic data. Geophysics, 85(4): WA13-WA26. DOI:10.1190/geo2019-0173.1 (  0) 0) |
Tong, S. Y., Wang, K., Yin, W. S., and Hu, W., 2021. Separation of marine seismic exploration streamer mixed data based on convolutional neural network. Periodical of Ocean University of China, 51(5): 81-87 (in Chinese with English abstract). (  0) 0) |
Tsingas, C., Almubarak, M. S., Jeong, W., Shuhail, A. A., and Trzesniowski, Z., 2020. 3D distributed and dispersed source array acquisition and data processing. Leading Edge, 39(6): 392-400. DOI:10.1190/tle39060392.1 (  0) 0) |
Vaage, S. T., 2005. Method and system for acquiring marine seismic data using multiple seismic sources. U.S. Patent 69 06981, 2005-6-14, DOI: 10.1190/tle39060392.1.
(  0) 0) |
Wang, S., Hu, W., Yuan, P., Wu, X., Zhang, Q., Nadukandi, P., et al., 2021. Seismic deblending by self-supervised deep learning with a blind-trace network. First International Meeting for Applied Geoscience & Energy Expanded Abstracts, 2021. Denver, SEG-2021-3583662.
(  0) 0) |
Wang, Z., Cun, X., Bao, J., Zhou, W., Liu, J., and Li, H., 2022. Uformer: A general U-Shaped transformer for image restoration. 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). New Orleans, 17662-17672.
(  0) 0) |
Xu, L. L., Di, Z. X., Shi, T. K., Duan, W. W., Huang, L., Ding, J. Q., et al., 2023. Separation of seismic blending data for borehole explosive source simultaneous shooting. Geophysical Prospecting for Petroleum, 62(2): 281-296 (in Chinese with English abstract). (  0) 0) |
Zhang, C. J., Hu, J. X., Wei, Y. J., Wang, Z. K., Wang, C. W., and Cao, J. J., 2022. Study of simultaneous source data deblending based on improved DnCNN. Journal of Hebei GEO University, 45(6): 41-48 (in Chinese with English abstract). (  0) 0) |
Zhang, H., Zhang, X. B., and Yang, Z. X., 2023a. Land wellseismic source blended data separation technology. Proceedings of the Fifth Annual Symposium on Oil and Gas Geophysics. Quanzhou, 4pp (in Chinese with English abstract).
(  0) 0) |
Zhang, Q., Abma, R., and Ahmed, I., 2013. A marine node simultaneous source acquisition trial at Atlantis, Gulf of Mexico. SEG Technical Program Expanded Abstracts. Houston, 99-103, DOI: 10.1190/segam2013-0699.1.
(  0) 0) |
Zhang, Q. H., Wang, M. X., Wu, A. C., Zhu, L. B., and Chen, W. J., 2023b. High-efficiency wide-azimuth acquisition test at seasimulation and signal separation. Marine Geology Frontiers, 39(6): 93-100 (in Chinese with English abstract). (  0) 0) |
Zhang, Z., Xuan, Y., Wei, Y., Ge, Q., and Han, L., 2017. Seismic data deblending based on the trilateral filter. 2017 SEG International Exposition and Annual Meeting. Houston, SEG-2017-17751909.
(  0) 0) |
Zhao, H., Gallo, O., Frosio, I., and Kautz, J., 2017. Loss functions for image restoration with neural networks. IEEE Transactions on Computational Imaging, 3(1): 47-57. DOI:10.1109/TCI.2016.2644865 (  0) 0) |
Zhou, L., Zhuang, Z., Cheng, J. W., and Gu, H. M., 2016. Using adaptive iterative multi-level median filtering method to separate offshore multi-source mixed wave field. Oil Geophysical Prospecting, 51(3): 434-443 (in Chinese with English abstract). (  0) 0) |
Zu, S. H., Cao, J., Qu, S., and Chen, Y., 2020. Iterative deblending for simultaneous source data using the deep neural network. Geophysics, 85(2): V131-V141. DOI:10.1190/geo2019-0319.1 (  0) 0) |
Zu, S. H., Zhou, H., Chen, Y. K., Qu, S., Zou, X., Chen, H. L., et al., 2016a. A periodically varying code for improving deblending of simultaneous sources in marine acquisition. Geophysics, 81(3): V213-V225. DOI:10.1190/geo2015-0447.1 (  0) 0) |
Zu, S. H., Zhou, H., Chen, Y. K., Qu, S., Liu, R. W., and Chen, H. L., 2016b. Irregularly sampled multi-source data deblending based on shaping regularization. Oil Geophysical Prospecting, 51(2): 247-253 (in Chinese with English abstract). (  0) 0) |
 2025, Vol. 24
2025, Vol. 24


