2) Laboratory for Regional Oceanography and Numerical Modeling, Pilot National Laboratory for Marine Science and Technology, Qingdao 266237, China;
3) Key Laboratory of Marine Sciences and Numerical Modeling, Ministry of Natural Resources, Qingdao 266061, China
Vertical mixing plays a key role in regulating the temperature structure and circulation of oceans. Insufficient mixing in the upper ocean during summer is a common problem of oceanic circulation and climate models that usually results in extremely high sea surface temperatures (SSTs) and extremely low subsurface temperatures (Martin, 1985; Ezer, 2000; Huang et al., 2011). Huang et al., (2014) assessed the ability of 45 Coupled Model Inter-comparison Project Phase 5 (CMIP5; Taylor et al., 2012) models to simulate the surface mixed layer and found that the summer mixed layer depth (MLD) is significantly underestimated in most of these models. The authors thus suggested that this systematic underestimation of MLD is caused by insufficient upper-ocean vertical mixing in the climate models.
Surface gravity waves can greatly enhance the turbulence kinetic energy (TKE) and associated vertical mixing of the upper ocean through wave-breaking and non-breaking processes (Agrawal et al., 1992; Drennan et al., 1996; Young and Babanin, 2006) and effectively correct the problem of insufficient mixing (Huang et al., 2011; Qiao and Huang, 2012). Most of the wave energy is dissipated locally through wave breaking (Donelan, 1998). However, vertical mixing associated with wave breaking alone is insufficient to significantly improve simulations of the upper ocean (Zhang et al., 2007; Huang et al., 2011) because such mixing is mainly confined to the near-surface zone with a depth scale of the wave height (Rapp and Melville, 1990; Craig and Banner, 1994; Soloview and Lukas, 2003).
Recent research efforts have focused on the effects of non-breaking waves. Because surface waves are inherently nonlinear in real oceans, they are not truly potential waves prior to breaking (Phillips, 1961). Non-breaking surface waves can directly regulate turbulence and mixing in the upper ocean. Compared with breaking waves, non-breaking waves can influence larger depths and are more significant for upper-ocean mixing (Anis and Moum, 1995; Gemmrich and Farmer, 2004).
Langmuir circulations (LCs), which are associated with the Stokes drift induced by surface waves, are among the most obvious phenomena in the surface layer; they usually occur as organized large-scale convective motions in the sea surface. When LCs appear, they rapidly mix away near-surface stratifications, decrease the SST, and deepen the mixed layer (Weller and Price, 1988). Therefore, LCs are extensively used to improve simulations of the upper ocean, especially the MLD (Li et al., 1995; Li and Garrett, 1997; Kukulka et al., 2009; Belcher et al., 2012; Li et al., 2016; Ali et al., 2019). The available studies originated from large-eddy simulations (LESs) (Skyllingstad and Denbo, 1995; McWilliams et al., 1997; Noh et al., 2004) and were subsequently extended to oceanic circulation (D'Alessio et al., 1998; Kantha and Clayson, 2004) and climate (Dufresne et al., 2013; Fan and Griffies, 2014) models; here, non-breaking wave-induced mixing was attributed to effects of LCs (Leibovich and Paolucci, 1980; McWilliams et al., 1997; Grant and Belcher, 2009).
In the present paper, we assessed the role of LCs in upper-ocean mixing by examining their influences on upper-ocean thermal structures and then determined whether attributing non-breaking wave-induced mixing to the LCs is reasonable. In Section 2, we briefly review two parameterizations of the LCs used in subsequent sections. We then examined the effects of LCs on regulating the temperature profiles of the upper ocean by using a one-dimensional model in Section 3 and a three-dimensional model in Section 4. Four CMIP5 models consider the effects of LCs (Huang et al., 2014); in Section 5, the abilities of these models to simulate subsurface temperatures are analyzed. Section 6 provides the conclusions of this study.
2 Parameterization of LCsThe effects of LCs have been incorporated into various vertical mixing schemes, such as the Price-Weller-Pinkel model (Li et al., 1995; Li and Garrett, 1997), the turbulence closure model (D'Alessio et al., 1998; Axell, 2002; Kantha and Clayson, 2004), and the K-profile parameterization model (McWilliams and Sullivan, 2000; Smyth et al., 2002). Most classical turbulence closure models add an additional turbulence production term associated with the Stokes drift. Kantha and Clayson (2004) incorporated the effects of LCs into the Mellor-Yamada (M-Y) turbulence model (Mellor and Yamada, 1982), in which the two prognostic equations for q2 and q2l are as follows:
| $\frac{D}{{Dt}}(\frac{{{q^2}}}{2}) - \frac{\partial }{{\partial z}}[{K_q}\frac{\partial }{{\partial z}}(\frac{{{q^2}}}{2})] = {P_S} + {P_{{\rm{Stokes}}}} + {P_b} - \varepsilon, $ | (1) |
| $\frac{{D{q^2}l}}{{Dt}} - \frac{\partial }{{\partial z}}[{K_q}\frac{{\partial {q^2}l}}{{\partial z}}] = {E_1}l[{P_S} + {E_3}{P_b}] + {E_6}l{P_{{\rm{Stokes}}}} - l\varepsilon \tilde W, $ | (2) |
where q2/2 is the TKE; l is a turbulence length scale; Kq is the vertical turbulence diffusivity; PS is the shear production of the mean current; Pb is the buoyant production;
The turbulence production associated with the Stokes drift can be written as
| ${P_{{\rm{Stokes}}}} = - \overline {u'w'} \frac{{\partial {u_s}}}{{\partial z}} - \overline {v'w'} \frac{{\partial {v_s}}}{{\partial z}}, $ | (3) |
where us and vs are the Stokes drift velocities and u' and v' are the fluctuations of horizontal velocity components.
In this scheme, a new constant E6 is introduced. Harcourt (2013) showed that selecting a value for E6 presents a tuning dilemma between minimizing errors in predicting the mixing length and minimizing errors in predicting TKE. E6 is expected to be of the order of magnitude of E1 (Soloviev and Kukas, 2006). However, increases in the vertical mixing coefficient strongly depend on this constant in this scheme (Kantha and Clayson, 2004); thus, it is usually set to 7.2 (Kantha et al., 2010), which is much larger than E1 (usually set to 1.8), to fit the LES results of McWilliams et al. (1997).
Axell (2002) introduced the effects of LCs into a k-ε turbulence closure model in which the turbulence behavior induced by LCs is similar to those induced by the mean current shear and internal waves. The total shear production is
| $P_S^{{\rm{tot}}} = {P_S} + {P_L} + {P_{IW}}, $ | (4) |
where PIW is the turbulence production induced by breaking internal waves and PL is the shear production by LCs, which is given by
| ${P_L}(z) = \frac{{w_L^3(z)}}{{{H_L}}}, $ | (5) |
where the HL is assumed to be the depth to which a water parcel with kinetic energy
| $- \int_{ - {H_L}}^0 {{N^2}(z)z{\rm{d}}z = \frac{1}{2}u_S^2}, $ | (6) |
in which N(z) is the local buoyancy frequency. Moreover,
| ${w_L} = \left\{ \begin{array}{l} {c_L}{u_S}\sin \left({\frac{{ - {\rm{ \mathit{ π} }}z}}{{{H_L}}}} \right){\rm{\;\;\;\;\;\;\;\;if }} - z \le {H_L}\\ 0{\rm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;otherwise}} \end{array} \right., $ | (7) |
is the velocity scale associated with the LCs and cL is a non-dimensional constant usually set to 0.15.
3 One-Dimensional Experiments 3.1 Model DescriptionIn this section, a one-dimensional model is used to examine the behavior of LCs compared with field observations from June 2007 to January 2008 taken from Ocean Weather Station Papa, which is located in the eastern North Pacific at 145°W, 50°N. This model is similar to that used by Mellor and Blumberg (2004). The water depth is set to 200 m with a model vertical resolution of 2 m. The initial temperature and salinity are taken from values recorded on June 9, 2007 and linearly interpolated to the model grid; the initial velocity is set to zero. Hourly surface data are used to force the numerical model. Because a net surface heat imbalance was previously found at this site (Large et al., 1994), 15 W m−2 is added to the outgoing heat flux to decrease the simulated deviation. In addition, the SST and sea surface salinity (SSS) are relaxed to the field observations, with relaxations of 50 W m−2 K−1 for SST and 30 days for SSS (assuming a MLD of 25 m). Other details are provided in Huang et al. (2011).
Three cases, named experiment Por, experiment PL, and experiment PLW, were carried out to evaluate the effects of LCs on the upper ocean (Table 1). The first case is based on the original M-Y scheme, in which the effects of surface waves are not included. In the second case, the scheme of Kantha and Clayson (2004) is used to describe LC effects. Some studies have suggested that the combined effects of LCs and wave breaking can produce strong vertical mixing in the upper ocean (Sullivan et al., 2007). Therefore, wave-breaking effects are considered in the third case, in which the scheme of Mellor and Blumberg (2004) is used.
|
|
Table 1 Experiments conducted by using one-dimensional and three-dimensional models |
The most notable features induced by insufficient upper-ocean vertical mixing are a too-sharp model summertime thermocline and its associated too-cold subsurface temperature (Ezer, 2000; Huang et al., 2011). Fig. 1 shows simulated and observed daily-mean upper-ocean temperature profiles. As expected, the summertime thermocline in experiment Por is shallower and sharper in comparison with field observations due to insufficient vertical mixing. This unrealistic thermocline results in an overly low simulated subsurface temperature in summer. The maximum bias of the subsurface temperature can reach up to −4℃ in experiment Por (Fig. 2a).
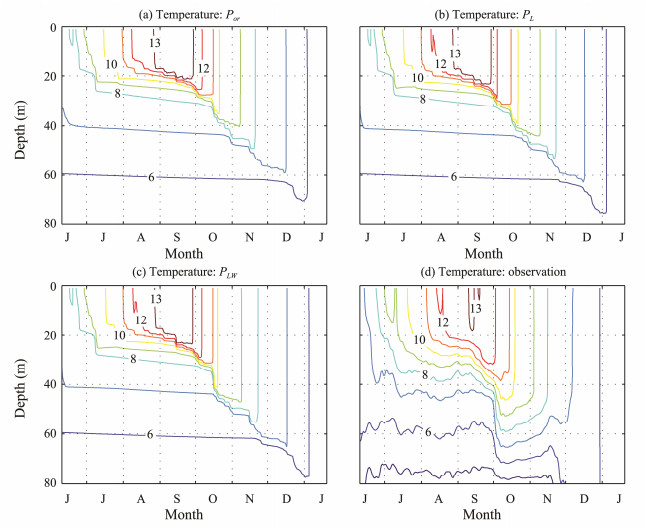
|
Fig. 1 Simulated and observed daily-mean temperature profiles (unit: ℃) at Station Papa from June 2007 to January 2008. (a), Experiment Por; (b), experiment PL; (c), experiment PLW; and (d), field observations. The simulations are based on a one-dimensional model. |
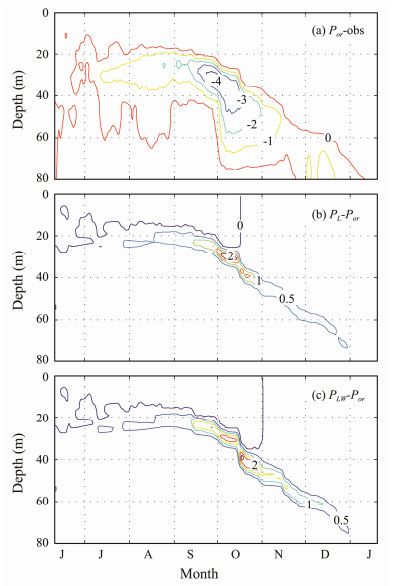
|
Fig. 2 Simulated daily-mean temperature deviations (unit: ℃). (a), Experiment Por minus field observations; (b), experiment PL minus experiment Por; and (c), experiment PLW minus experiment Por. The simulations are based on a one-dimensional model. |
The cold bias is somewhat reduced when LC effects are included. However, this improvement is mainly limited to the base of the mixed layer, and its maximum value is only 2℃ (Fig. 2b). The combination of LCs and wave breaking enhances their individual roles and transfers more energy into deep layers (Sullivan et al., 2007; Li et al., 2013). When LCs work together with wave breaking, the simulations seem to be improved, and the maximum increase in subsurface temperature is also 2℃ when compared with experiment Por (Fig. 2c). Therefore, all three cases fail to produce a reasonable thermal structure regardless of the inclusion of LC effects (Fig. 1).
Too-warm model SSTs and too-shallow MLDs are other problems associated with insufficient vertical mixing. Besides being affected by vertical mixing, the SST is also strongly influenced by the sea surface heat flux; thus, its simulated bias is usually smaller than that of the subsurface layer. The simulated SST is overestimated by approximately 0.5℃ from June to October in experiment Por (Fig. 3), which is much smaller than the bias in the subsurface layer. When LC effects are included, the SST decreases slightly and the MLD increases. The changes are approximately 0.1℃ for SST and 2 m for MLD when LC effects alone are considered (Fig. 3). The maximum changes can reach up to 0.2℃ for SST and 7 m for MLD when LCs work together with wave breaking. From November to January, the SST increases slightly when LCs are considered on account of the increase in heat content of the upper ocean with increasing subsurface temperature, which slows down the surface cooling process in winter.
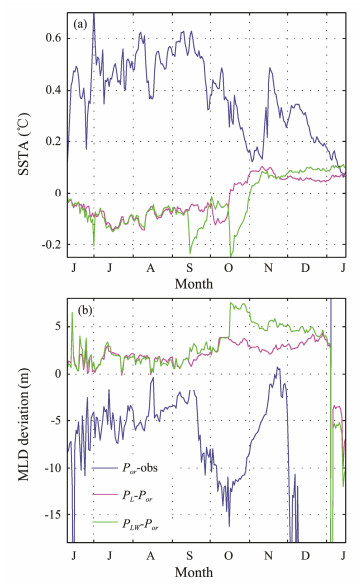
|
Fig. 3 Simulated daily-mean (a) SSTA and (b) MLD deviations between experiment Por and field observations (blue curves), experiment PL and experiment Por (pink curves), and experiment PLW and experiment Por (green curves). MLD is defined as the depth at which the temperature drops by 0.5℃ compared with the surface value. The simulations are based on a one-dimensional model. |
The magnitudes of changes in SST and MLD are in accordance with previous studies (Li et al., 1995; D'Alessio et al., 1998; Carniel et al., 2005; Kukulka et al., 2009; Li et al., 2013), although most of them argue that LCs play an important role in the upper ocean. For example, D'Alessio et al. (1998) used a similar turbulence closure scheme and observations from Station Papa to show that the maximum change in SST is about 0.2℃ in the cases with and without LC effects. Kukulka et al. (2009) simulated an LC growth event using a LES model in which the change in SST was actually smaller than 0.1℃ although the MLD deepened. In fact, observations by Li et al. (1995) and Kukulka et al. (2009) also showed that changes in SST are actually smaller than 0.1℃ under the effect of LCs.
Fig. 4 shows the simulated daily-mean vertical mixing profiles in experiment Por and their deviations from the two other experiments. In these cases, when LCs are incorporated into the model, the simulated vertical mixing is greatly enhanced. However, because these effects are mainly confined to the mixed layer, their ability to regulate the upper-ocean thermal structure is limited.
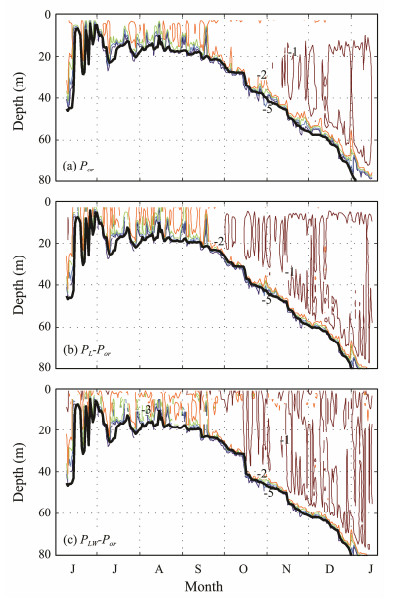
|
Fig. 4 Simulated daily-mean vertical mixing coefficients as a function of depth and time in (a) experiment Por, and their deviations (b) experiment PL minus experiment Por, and (c) experiment PLW minus experiment Por. The denary logarithm of the mixing coefficient (unit: m2 s−1) is shown, and the thick black curve indicates the simulated MLD. The simulations are based on a one-dimensional model. |
The behavior of LCs was further assessed by examining simulated subsurface temperatures using the three-dimensional Princeton Ocean model (Blumberg and Mellor, 1987). The model domain covers the global ocean between 72°S and 65°N with a zonal resolution of 1°. The meridional resolution is 1/3° within 10°S–10°N and increases linearly to 1° at 20°N (20°S). The model includes 32 sigma layers in the vertical direction with at least 6 layers in the top 60 m and at least 10 additional levels between 60 and 250 m. The bottom topography is obtained from ETOPO5, and the maximum water depth is set to 5000 m.
The model is initiated by using the temperature and salinity conditions in January taken from the WOA01 climatology (Conkright at al., 2002). The climatological monthly-mean wind stress is taken from the data of QSCAT/ NCEP blended ocean winds from 2000 to 2005 (Milliff et al., 2004). The surface heat and freshwater fluxes are taken from the monthly-mean COADS climatology (da Silva et al., 1994). The SST and SSS are relaxed to the monthly-mean WOA01 climatology, with relaxations of 50W m−2 K−1 for SST and 60 d for SSS (for a MLD of 25 m), to prevent surface density values from drifting too far from the climatology. Similar to Section 3, three experiments, named as Gor, GL, and GLW, were also carried out (Table 1). Each case was integrated for 12 years from a state of rest, and the outputs of the model in the last three years are used to analyze LC effects.
4.2 ResultsFig. 5 shows monthly-mean temperature differences along 170°W in August for the three cases. Vertical mixing from surface waves is more important than that associated with the velocity shear of the mean current in the upper portion of extra-tropical oceans (Noh, 2004; Qiao and Huang, 2012). In experiment Gor, which does not consider the effects of surface waves, the simulated subsurface temperature is seriously underestimated due to insufficient mixing in the middle latitude between 20°N and 50°N when compared with the WOA01 climatological data. The maximum bias can reach up to 3℃ (Fig. 5a). The temperature change induced by LC effects alone shows an amplitude of 0.1℃ (Fig. 5b) and is consistently negligible in comparison with the large cold bias in experiment Gor. In experiment GLW, which considers the combined effects of LCs and wave breaking, the subsurface temperature increases greatly due mainly to the effects of wave breaking (Huang et al., 2011) and shows a maximum value of 2.5℃ (Fig. 5c). However, this change is mainly confined to the upper 60 m layer; thus, it is insufficient to correct the cold bias in the subsurface layer.
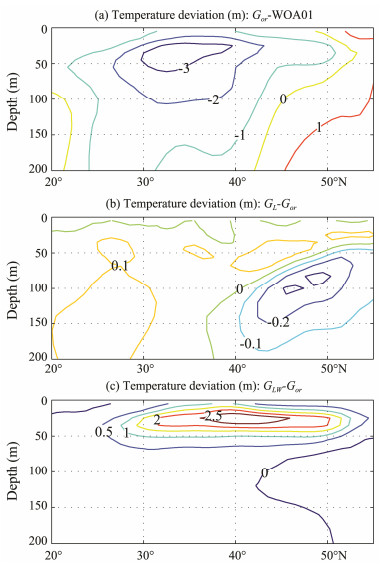
|
Fig. 5 Monthly-mean temperature differences (in ℃) along 170°W in August. (a), Experiment Gor minus WOA01; (b), experiment GL minus experiment Gor; and (c), experiment GLW minus experiment Gor. The experiments are based on a three-dimensional model. |
The behavior of LCs can also be seen in Fig. 6, which shows monthly-mean model temperature errors along 30°N in August for the three cases. The cold subsurface bias also results from an unrealistic thermocline (Fig. 7). Compared with the WOA01 climatology (Fig. 7d), the seasonal thermocline is much shallower and sharper for all three cases.
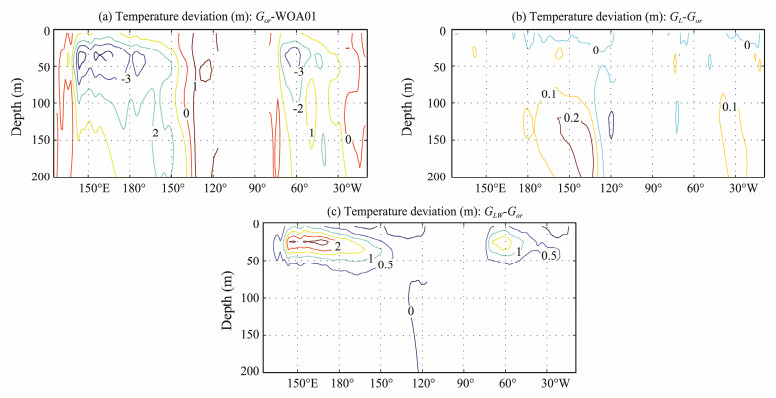
|
Fig. 6 Monthly-mean temperature differences (in ℃) along 30°N in August. (a), Experiment Gor minus WOA01; (b), experiment GL minus experiment Gor; and (c), experiment GLW minus experiment Gor. The experiments are based on a three-dimensional model. |
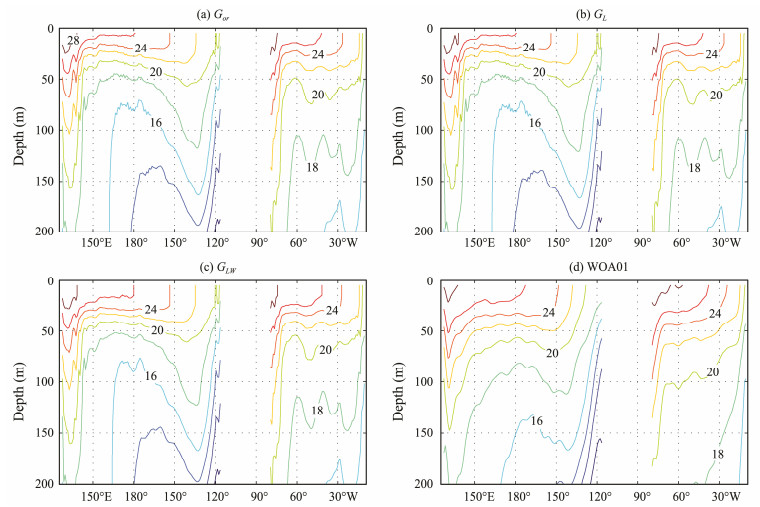
|
Fig. 7 Temperature distribution along 30°N in August from (a) experiment Gor, (b) experiment GL, (c) experiment GLW, and (d) the WOA01 climatology. The contour interval is 2℃. The experiments are based on a three-dimensional model. |
Fig. 8 shows the temperature profiles at the central point of the North Pacific Ocean (30°N, 170°W). The effects of LCs are too small to produce significant changes. Compared with experiment Gor, the simulated temperature seems to slightly increase at a depth of 100–200 m in experiment GL. In experiment GLW, the simulated temperature increases further, and the MLD increases remarkably; however, large deviations compared with field observations may still be found.
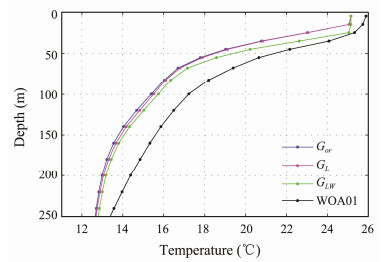
|
Fig. 8 Simulated and climatological monthly-mean temperature profiles in August at 30°N, 170°W. The simulations are based on a three-dimensional model. |
CMIP5 includes most of the state-of-the-art climate models and earth system models; four of the models in this project, namely, CNRM-CM5, IPSL-CM5A-LR, IPSL-CM5A-MR, and IPSL-CM5B-LR, consider LC effects (Huang et al., 2014). In these four models, the scheme of Axell (2002) is used to parameterize effects of LCs (Dufresne et al., 2013; Voldoire et al., 2013). In addition, the effects of surface wave breaking are also considered via the scheme of Mellor and Blumberg (2004). The effects of LCs are evaluated by using 20 years (1986–2005) of monthly-averaged outputs from historical runs with an ensemble number of r1i1p1. These historical runs refer to the 20th century simulation forced by observed atmospheric compositional changes, including both natural and anthropogenic sources.
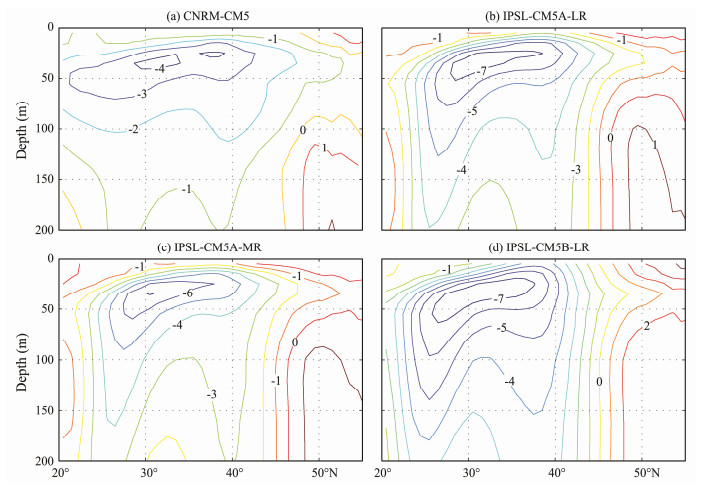
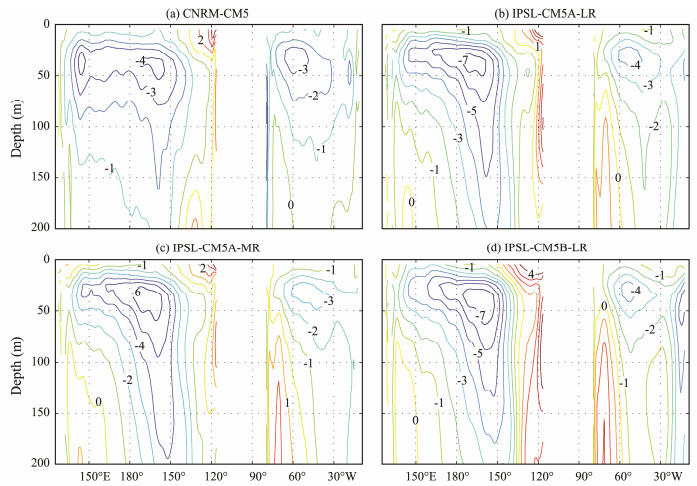
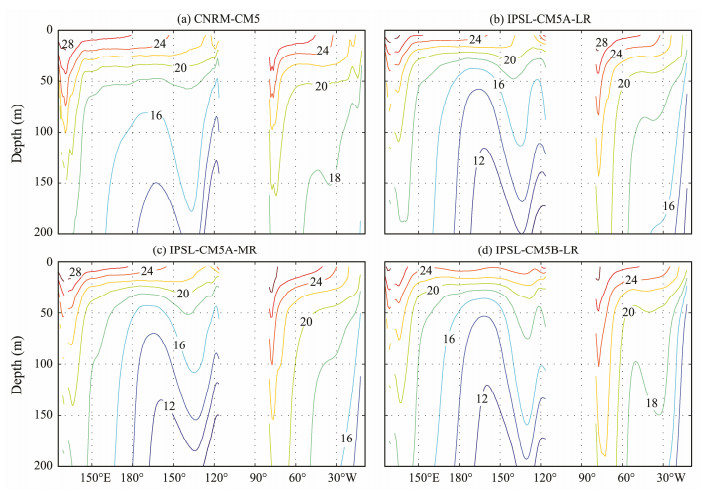
Too-cold subsurface temperatures are a common problem of climate models (Flato et al., 2013). Fig. 9 shows monthly-mean temperature differences along 170°W in August for these four models in comparison with the WOA01 climatology. All of the models simulate a toocold upper-ocean temperature. In the near-surface region, the biases of these models deviate by only approximately 1℃ from field observations. This finding implies that the models can well reproduce surface temperatures. However, simulated subsurface temperatures in the middle latitude are seriously underestimated when compared with actual observations. The maximum biases occur at depths between 20 and 60 m and are as large as 4℃ in CNRM-CM5 and 7℃ in the three other models. These large biases can also be observed in Fig. 10, which shows monthly-mean model temperature errors along 30°N in August. Similar to our earlier discussion, the cold subsurface bias can be associated with an unrealistic thermocline (Fig. 11). Compared with the WOA01 climatology (Fig. 7d), the simulated thermoclines are clearly much shallower and sharper in these four models.
|
Fig. 9 Monthly-mean temperature differences (in ℃) from the WOA01 climatology along 170°W in August. (a), CNRM-CM5; (b), IPSL-CM5A-LR; (c), IPSL-CM5A-MR; and (d), IPSL-CM5B-LR. The data are obtained from CMIP5 climate models. |
|
Fig. 10 Monthly-mean temperature differences (in ℃) from the WOA01 climatology along 30°N in August. (a), CNRM-CM5; (b), IPSL-CM5A-LR; (c), IPSL-CM5A-MR; and (d), IPSL-CM5B-LR. The data are obtained from CMIP5 climate models. |
|
Fig. 11 Temperature distribution along 30°N in August determined from (a) CNRM-CM5, (b) IPSL-CM5A-LR, (c) IPSL-CM5A-MR, and (d) IPSL-CM5B-LR. The contour interval is 2℃. The data are obtained from CMIP5 climate models. |
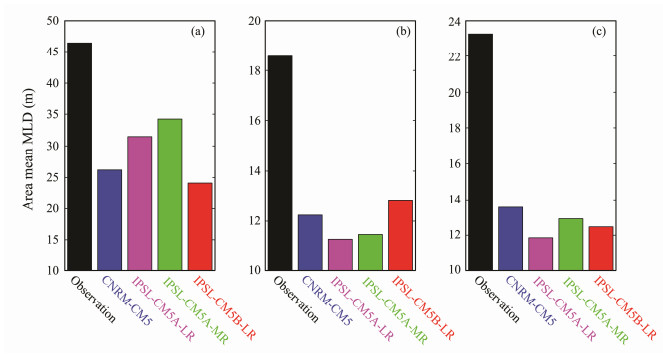
Due to the cold subsurface temperature, summer MLDs are significantly underestimated in the four models, especially in the central North Pacific and Atlantic Oceans (Fig. 12 or Huang et al., 2014). This finding is similar to those of Fan and Griffies (2014) and D'Asaro et al. (2014), who showed that the effects of LCs are insignificant to increases in MLD in summer.
|
Fig. 12 Area-averaged MLDs (a) in austral summer in the Southern Ocean (between 30°S and 65°S), (b) in boreal summer in the central Northern Pacific Ocean (35°S–55°S, 160°E–140°W), and (c) in boreal summer in the central Northern Atlantic (40°S–65°S, 50°W–10°W) determined from four CMIP5 climate models and field observations. MLD is defined as the depth in which the potential density deviates by 0.03 kg m−3 from its value at 10 m. The observed MLDs are taken from the climatological monthly MLD data of de Boyer Montégut et al. (2004). |
In fact, although LCs can rapidly destroy near-surface stratification and increase the MLD (Li et al., 1995; Kukulka et al., 2009), their effects seem to be mostly confined to the initial stages of MLD growth (Skyllingstad et al., 2000). Noh et al. (2011) argued that LCs could significantly increase the MLD only if the latter is shallow and the buoyancy jump across the mixed layer is small. Field observations by Weller and Price (1988) showed that the effects of LCs are confined to the upper part of the mixed layer, insignificant in the lower part, and absent in the relict mixed layer during summer-like conditions or deeper mixed layer during stormy conditions.
6 Discussion and ConclusionsIn this paper, the influences of LCs on the upper-ocean thermal structure are examined by using one- and three-dimensional ocean circulation models, as well as four climate models from the CMIP5. The results show that LCs can slightly improve simulations of MLD and SST in the models; however, their effect on the upper ocean is not sufficiently large to produce significant changes. The models evaluated in this work, including those considering LC effects alone and the combined effects of LCs and wave breaking, failed to produce a reasonable summertime thermocline, resulting in a large cold bias in the subsurface layer. A cold bias is a typical feature induced by insufficient vertical mixing in the upper ocean. Our findings imply that LCs are insufficient to solve the problem of insufficient vertical mixing and that restriction of non-breaking surface wave-induced mixing in LCs may be questionable.
In this study, only two early parameterization schemes of LCs, i.e., those of Kantha and Clayson (2004) and Axell (2002), were analyzed. LCs were studied extensively with LES in the past, and many new schemes have since been proposed. However, the performances of LCs in these new schemes are very similar as those in the present study. Although all researchers claim that their schemes can enhance the vertical mixing of the upper ocean and produce significantly improved simulations of MLD and SST, the improvements observed are, in fact, very limited and large deviations are still recorded. For example, Ali et al. (2019; see their Table 2) investigated the performances of five LC schemes, including those of McWilliams and Sullivan (2000), Smyth et al. (2002), Takaya et al. (2010), Van Roekel et al. (2012), and Li and Fox-Kemper (2017), by using a numerical model of the North Atlantic and Arctic Oceans and found that mean MLDs during summer increase from 4.2% to 14.6% in the model domain south of 50°N relative to the case without wave effects.
Our conclusions are only based on numerical model results, which depend on the behaviors of the models and the parameterization of LCs used. Therefore, further studies, especially those involving field observations, are needed to comprehensively understand the effects of LCs on the upper ocean. In addition, studying non-breaking surface wave-induced mixing from a more comprehensive perspective (Veron et al., 2009; Ghantous and Babanin, 2014; Qiao et al., 2016), rather than LCs alone, is necessary to simulate the upper ocean accurately.
AcknowledgementsData of the CMIP5 models are available at https://esgf-data.dkrz.de/search/cmip5-dkrz/. CJH and DD were supported by the National Key Research and Development Program of China (No. 2017YFC1404000), the Basic Scientific Fund for National Public Research Institutes of China (No. 2018S03), and the National Natural Science Foundation of China (Nos. 41776038 and 41376036). Dr. Fangli Qiao was supported by the Natural Science Foundation of China (Nos. 41821004).
Agrawal, Y. C., Terray, E. A., Donelan, M. A., Hwang, P. A., Williams III, A. J., Drennan, W. M., Kahma, K. K. and Kitaigorodskii, S. A., 1992. Enhanced dissipation of kinetic energy beneath surface waves. Nature, 359: 219-220. (  0) 0) |
Ali, A., Christensen, K. H., Breivik, Ø., Malila, M., Raj, R. P., Bertino, L., Chassignet, E. P. and Bakhoday-Paskyabi, M., 2019. A comparison of Langmuir turbulence parameterizations and key wave effects in a numerical model of the North Atlantic and Arctic Oceans. Ocean Modelling, 137: 76-97. (  0) 0) |
Anis, A. and Moum, J. N., 1995. Surface wave-turbulence interactions: Scaling ε (z) near the sea surface. Journal of Physical Oceanography, 25: 2025-2045. (  0) 0) |
Axell, L. B., 2002. Wind-driven internal waves and Langmuir circulations in a numerical ocean model of the southern Baltic Sea. Journal of Geophysical Research, 107(C11): 3204. DOI:10.1029/2001JC000922 (  0) 0) |
Belcher, S. E., Grant, A. L. M., Hanley, K. E., Fox-kemper, B., Roekel, L. V., Sullivan, P. P., Large, W. G., Brown, A., Hines, A., Calvert, D., Rutgersson, A., Pettersson, H., Bidlot, J.-R., Janssen, P. A. E. M. and Polton, J. A., 2012. A global perspective on Langmuir turbulence in the ocean surface boundary layer. Geophysical Research Letters, 39: L18605. DOI:10.1029/2012GL052932 (  0) 0) |
Blumberg, A. F., and Meller, G. L., 1987. A description of a three-dimensional coastal ocean circulation model. In: Three-Dimensional Coastal Ocean Models (Chapter 4). Heaps, N. S., ed., American Geophysical Union, Washington, D.C., 1-16.
(  0) 0) |
Carniel, S., Sclavo, M., Kantha, L. H. and Clayson, C. A., 2005. Langmuir cells and mixing in the upper ocean. Nuovo Cimento della Societa Italiana di Fisica C, 28: 33-54. (  0) 0) |
Conkright, M. E., Locarnini, R. A., Garcia, H. E., O'Brien, T., Boyer, T. P., Stephens, C., and Antonov, J. I., 2002. World Ocean Atlas 2001: Objective Analyses, Data Statistics, and Figures. National Oceanographic Data Center, Silver Spring, MD, Internal Report 17, 17pp.
(  0) 0) |
Craig, P. D. and Banner, M. L., 1994. Modeling wave-enhanced turbulence in the ocean surface layer. Journal of Physical Oceanography, 24: 2546-2559. (  0) 0) |
DoAlessio, S. J. D., Abdella, K. and McFarlane, N. A., 1998. A new second-order turbulence closure scheme for modelling the ocean mixed layer. Journal of Physical Oceanography, 28: 1624-1641. DOI:10.1175/1520-0485(1998)0282.0.CO;2 (  0) 0) |
DoAsaro, E. A., Thomson, J., Shcherbina, A. Y., Harcourt, R. R., Cronin, M. F., Hemer, M. A. and Fox-Kemper, B., 2014. Quantifying upper ocean turbulence driven by surface waves. Geophysical Research Letters, 41: 102-107. DOI:10.1002/2013GL058193 (  0) 0) |
da Silva, A., Young, A. C., and Levitus, S., 1994. Atlas of Surface Marine Data 1994, Volume 1: Algorithms and Procedures. NOAA Atlas NESDIS 6, U.S. Department of Commerce, Washington, D.C., 83pp.
(  0) 0) |
de Boyer Montégut, C., Madec, G., Fischer, A. S., Lazar, A. and Iudicone, D., 2004. Mixed layer depth over the global ocean: An examination of profile data and a profile-based climatology. Journal of Geophysical Research, 109: C12003. DOI:10.1029/2004JC002378 (  0) 0) |
Donelan, M. A., 1998. Air-water exchange processes. In: Physical Processes in Lakes and Oceans (Chapter 2). Imberger, J., ed., American Geophysical Union, Washington, D.C., 19-36.
(  0) 0) |
Drennan, W. M., Donelan, M. A., Terray, E. A. and Katsaros, K. B., 1996. Oceanic turbulence dissipation measurements in SWADE. Journal of Physical Oceanography, 26: 808-815. (  0) 0) |
Dufresne, J.-L., Foujols, M.-A., Denvil, S., Caubel, A., Marti, O., Aumont, O., Balkanski, Y., Bekki, S., Bellenger, H., Benshila, R., Bony, S., Bopp, L., Braconnot, P., Brockmann, P., Cadule, P., Cheruy, F., Codron, F., Cozic, A., Cugnet, D., de Noblet, N., Duvel, J.-P., Ethé, C., Fairhead, L., Fichefet, T., Flavoni, S., Friedlingstein, P., Grandpeix, J.-Y., Guez, L., Guilyardi, E., Hauglustaine, D., Hourdin, F., Idelkadi, A., Ghattas, J., Joussaume, S., Kageyama, M., Krinner, G., Labetoulle, S., Lahellec, A., Lefebvre, M.-P., Lefevre, F., Levy, C., Li, Z. X., Lloyd, J., Lott, F., Madec, G., Mancip, M., Marchand, M., Masson, S., Meurdesoif, Y., Mignot, J., Musat, I., Parouty, S., Polcher, J., Rio, C., Schulz, M., Swingedouw, D., Szopa, S., Talandier, C., Terray, P., Viovy, N. and Vuichard, N., 2013. Climate change projections using the IPSL-CM5 Earth System Model: From CMIP3 to CMIP5. Climate Dynamics, 40: 2123-2165. DOI:10.1007/s00382-012-1636-1 (  0) 0) |
Ezer, T., 2000. On the seasonal mixing layer simulated by a basin-scale ocean model and the Mellor-Yamada turbulence scheme. Journal of Geophysical Research, 105: 16843-16855. (  0) 0) |
Fan, Y. and Griffies, S. M., 2014. Impacts of parameterized Langmuir turbulence and non-breaking wave mixing in global climate simulations. Journal of Climate, 27: 4752-4775. (  0) 0) |
Flato, G., Marotzke, J., Abiodun, B., Braconnot, P., Chou, S. C., Collins, W., Cox, P., Driouech, F., Emori, S., Eyring, V., Forest, C., Gleckler, P., Guilyardi, E., Jakob, C., Kattsov, V., Reason, C., and Rummukainen, M., 2013. Evaluation of climate models. In: Climate Change 2013: The Physical Science Basis. Stocker, T. F., et al., eds., Cambridge University Press, Cambridge, United Kingdom and New York, NY, 741-866.
(  0) 0) |
Gemmrich, J. R. and Farmer, D. M., 2004. Near-surface turbulence in the presence of breaking waves. Journal of Physical Oceanography, 34: 1067-1086. (  0) 0) |
Ghantous, M. and Babanin, A. V., 2014. Ocean mixing by wave orbital motion. Acta Physica Slovaca, 64(1): 1-56. (  0) 0) |
Grant, A. L. M. and Belcher, S. E., 2009. Characteristics of Langmuir turbulence in the ocean mixed layer. Journal of Physical Oceanography, 39: 1871-1887. (  0) 0) |
Harcourt, R. R., 2013. A second-moment closure model of Langmuir turbulence. Journal of Physical Oceanography, 43: 673-697. DOI:10.1175/JPO-D-12-0105.1 (  0) 0) |
Huang, C. J., Qiao, F. L. and Dai, D. J., 2014. Evaluating CMIP5 simulations of mixed layer depth during summer. Journal of Geophysical Research: Oceans, 119: 2568-2582. DOI:10.1002/2013JC009535 (  0) 0) |
Huang, C. J., Qiao, F. L., Song, Z. Y. and Ezer, T., 2011. Improving simulations of the upper ocean by inclusion of surface waves in the Mellor-Yamada turbulence scheme. Journal of Geophysical Research, 116: C01007. DOI:10.1029/2010JC006320 (  0) 0) |
Kantha, L. H. and Clayson, C. A., 2004. On the effect of surface gravity waves on mixing in the oceanic mixed layer. Ocean Modelling, 6: 101-124. (  0) 0) |
Kantha, L. H., Lass, U. and Prandke, H., 2010. A note on Stokes production of turbulence kinetic energy in the oceanic mixed layer: Observations in the Baltic Sea. Ocean Dynamics, 60: 171-180. DOI:10.1007/s10236-009-0257-7 (  0) 0) |
Kukulka, T., Plueddemann, A. J., Trowbridge, J. H. and Sullivan, P. P., 2009. Significance of Langmuir circulation in upper ocean mixing: Comparison of observations and simulations. Geophysical Research Letters, 36: L10603. DOI:10.1029/2009GL037620 (  0) 0) |
Large, W. G., McWilliams, J. C. and Doney, S. C., 1994. Oceanic vertical mixing: A review and a model with a nonlocal boundary layer parameterization. Reviews of Geophysics, 32: 363-403. (  0) 0) |
Leibovich, S. and Paolucci, S., 1980. The Langmuir circulation instability as a mixing mechanism in the upper ocean. Journal of Physical Oceanography, 10: 186-207. (  0) 0) |
Li, M. and Garrett, C., 1997. Mixed layer deepening due to Langmuir circulation. Journal of Physical Oceanography, 27: 121-132. (  0) 0) |
Li, M., Zahariev, K. and Garrett, C., 1995. Role of Langmuir circulation in the deepening of the ocean surface mixed layer. Science, 270(5244): 1955-1957. (  0) 0) |
Li, Q. and Fox-Kemper, B., 2017. Assessing the effects of Langmuir turbulence on the entrainment buoyancy flux in the ocean surface boundary layer. Journal of Physical Oceanography, 47(12): 2863-2886. (  0) 0) |
Li, Q., Webb, A., Fox-Kemper, B., Craig, A., Danabasoglu, G., Large, W. G. and Vertenstein, M., 2016. Langmuir mixing effects on global climate: WAVEWATCH Ⅲ in CESM. Ocean Modelling, 103: 145-160. (  0) 0) |
Li, S., Song, J. and Fan, W., 2013. Effect of Langmuir circulation on upper ocean mixing in the South China Sea. Acta Oceanologica Sinica, 32(3): 28-33. DOI:10.1007/s13131-013-0285-5 (  0) 0) |
Martin, P. J., 1985. Simulation of the mixed layer at OWS November and Papa with several models. Journal of Geophysical Research, 90: 581-597. DOI:10.1029/JB090iB01p00581 (  0) 0) |
McWilliams, J. C. and Sullivan, P. P., 2000. Vertical mixing by Langmuir circulations. Spill Science & Technology Bulletin, 6: 225-237. (  0) 0) |
McWilliams, J. C., Sullivan, P. P. and Moeng, C.-H., 1997. Langmuir turbulence in the ocean. Journal of Fluid Mechanics, 334: 1-33. DOI:10.1017/S0022112096004375 (  0) 0) |
Mellor, G. and Blumberg, A., 2004. Wave breaking and ocean surface layer thermal response. Journal of Physical Oceanography, 34: 693-698. DOI:10.1175/2517.1 (  0) 0) |
Mellor, G. and Yamada, T., 1982. Development of a turbulence closure model for geophysical fluid problems. Reviews of Geophysics, 20: 851-875. DOI:10.1029/RG020i004p00851 (  0) 0) |
Milliff, R. F., Morzel, J., Chelton, D. B. and Freilich, M. H., 2004. Wind stress curl and wind stress divergence biases from rain effects on QSCAT surface wind retrievals. Journal of Atmospheric and Oceanic Technology, 21: 1216-1231. DOI:10.1175/1520-0426(2004)021<1216:WSCAWS>2.0.CO;2 (  0) 0) |
Noh, Y., 2004. Sensitivity to wave breaking and the Prandtl number in the ocean mixed layer model and its dependence on latitude. Geophysical Research Letters, 31: L23305. DOI:10.1029/2004GL021289 (  0) 0) |
Noh, Y., Goh, G. and Raasch, S., 2011. Influence of Langmuir circulation on the deepening of the wind-mixed layer. Journal of Physical Oceanography, 41: 472-484. DOI:10.1175/2010JPO4494.1 (  0) 0) |
Noh, Y., Min, H. S. and Raasch, S., 2004. Large eddy simulation of the ocean mixed layer: The effects of wave breaking and Langmuir circulation. Journal of Physical Oceanography, 34: 720-735. DOI:10.1175/1520-0485(2004)034<0720:LESOTO>2.0.CO;2 (  0) 0) |
Phillips, O. M., 1961. A note on the turbulence generated by gravity waves. Journal of Geophysical Research, 66: 2889-2893. DOI:10.1029/JZ066i009p02889 (  0) 0) |
Qiao, F. L. and Huang, C. J., 2012. Comparison between vertical shear mixing and surface wave-induced mixing in the extratropical ocean. Journal of Geophysical Research, 117: C00J16. DOI:10.1029/2012JC007930 (  0) 0) |
Qiao, F. L., Yuan, Y. L., Deng, J., Dai, D. J. and Song, Z. Y., 2016. Wave-turbulence interaction-induced vertical mixing and its effects in ocean and climate models. Philosophical Transactions of the Royal Society AɃMathematical and Physical and Engineering Sciences, 374: 20150201. (  0) 0) |
Rapp, R. J. and Melville, W. K., 1990. Laboratory measurements of deep-water breaking waves. Philosophical Transactions of the Royal Society of London Series AɃMathematical and Physical Sciences, A331: 735-800. (  0) 0) |
Skyllingstad, E. D., Smyth, W. D. and Crawford, G., 2000. Resonant wind driven mixing in the ocean boundary layer. Journal of Physical Oceanography, 30: 1866-1890. DOI:10.1175/1520-0485(2000)030<1866:RWDMIT>2.0.CO;2 (  0) 0) |
Skyllingstad, E. and Denbo, D., 1995. An ocean large-eddy simulation of Langmuir circulations and convection in the surface mixed layer. Journal of Geophysical Research, 100: 8501-8522. DOI:10.1029/94JC03202 (  0) 0) |
Smyth, W. D., Skyllingstad, E. D., Crawford, G. B. and Wijesekera, H., 2002. Nonlocal fluxes and stokes drift effects in the K-profile parameterization. Ocean Dynamics, 52: 104-115. DOI:10.1007/s10236-002-0012-9 (  0) 0) |
Soloviev, A., and Lukas, R., 2006. The Near-Surface Layer of the Ocean: Structure, Dynamics and Applications. Springer, Dordrecht, Netherlands, 572pp.
(  0) 0) |
Soloview, A. and Lukas, R., 2003. Observation of wave-enhanced turbulence in the near-surface layer of the ocean during TOGA COARE. Deep-Sea Research I, 50: 371-395. DOI:10.1016/S0967-0637(03)00004-9 (  0) 0) |
Sullivan, P. P., McWilliams, J. C. and Melville, W. K., 2007. Surface gravity wave effects in the oceanic boundary layer: Large-eddy simulation with vortex force and stochastic breakers. Journal of Fluid Mechanics, 593: 405-452. DOI:10.1017/S002211200700897X (  0) 0) |
Takaya, Y., Bidlot, J.-R., Beljaars, A. C. M. and Janssen, P. A. E. M., 2010. Refinements to a prognostic scheme of skin sea surface temperature. Journal of Geophysical Research, 115: C06009. DOI:10.1029/2009JC005985 (  0) 0) |
Taylor, K. E., Stouffer, R. J. and Meehl, G. A., 2012. An overview of CMIP5 and the experiment design. Bulletin of the American Meteorological Society, 93: 485-498. DOI:10.1175/BAMS-D-11-00094.1 (  0) 0) |
Van Roekel, L. P., Fox-Kemper, B., Sullivan, P. P., Hamlington, P. E. and Haney, S. R., 2012. The form and orientation of Langmuir cells for misaligned winds and waves. Journal of Geophysical Research, 117(C5): C05001. DOI:10.1029/2011JC007516 (  0) 0) |
Veron, F., Melville, W. K. and Lenain, L., 2009. Measurements of ocean surface turbulence and wave-turbulence interactions. Journal of Physical Oceanography, 39: 2310-2323. DOI:10.1175/2009JPO4019.1 (  0) 0) |
Voldoire, A., Sanchez-Gomez, E., Salasy Mélia, D., Decharme, B., Cassou, C., Sénési, S., Valcke, S., Beau, I., Alias, A., Chevallier, M., Déqué, M., Deshayes, J., Douville, H., Fernandez, E., Madec, G., Maisonnave, E., Moine, M.-P., Planton, S., Saint-Martin, D., Szopa, S., Tyteca, S., Alkama, R., Belamari, S., Braun, A., Coquart, L. and Chauvin, F., 2013. The CNRM-CM5.1 global climate model: Description and basic evaluation. Climate Dynamics, 40: 2091-2121. DOI:10.1007/s00382-00011-1259-y (  0) 0) |
Weller, R. A. and Price, J. F., 1988. Langmuir circulation within the oceanic mixed layer. Deep-Sea Research, 35(5): 711-747. DOI:10.1016/0198-0149(88)90027-1 (  0) 0) |
Young, I. R. and Babanin, A. V., 2006. Spectral distribution of energy dissipation of wind-generated waves due to dominant wave breaking. Journal of Physical Oceanography, 36: 376-394. DOI:10.1175/JPO2859.1 (  0) 0) |
Zhang, S., Yuan, Y. and Zheng, Q., 2007. Modeling of the eddy viscosity by breaking waves. Acta Oceanologica Sinica, 26(6): 116-123. (  0) 0) |
 2020, Vol. 19
2020, Vol. 19


