1 Introduction

As a basic form of seawater motion, tides play an important role in ocean mixing (Munk and Wunsch, 1998). Studies indicate that one-third of barotropic tidal energy is dissipated in the deep ocean, whereas the remaining energy is lost directly to bottom friction in shallow seas and on the continental shelf (Egbert and Ray, 2001; Carter et al., 2012). Strong tidal currents are reduced near the bottom, thus creating a vertical shear. Shear-generated turbulence enhances vertical mixing, contributing to upward nutrient transportation and biological activities (Thorpe, 2007). Therefore, the knowledge of turbulent mixing induced by tidal currents near the bottom is important for understanding both physical motions and biochemical processes.

The eddy viscosity is an important parameter for quantifying the mixing structure in the bottom boundary layer. The eddy viscosity is estimated from the observed quantities, such as current velocity. Attempts have been made where eddy viscosity profiles are specified as vertically constant or linear (Prandle, 1982; Soulsby, 1983), or investigated relying on the turbulence closure model (Werner et al., 2003). Yoshikawa and Endoh (2015) compared three methods for estimating turbulent mixing structures. These methods are considered because the mean velocity profiles are determined by the mean eddy viscosity in the bottom boundary layer. Therefore, the mean eddy viscosity can be estimated by solving the Ekman balance equations using the least squares methods. Cao et al. (2017) proposed an alternative scheme consisting of the bottom Ekman boundary layer model and its adjoint model as well as a minimization algorithm. They validated its performance with twin experiments but did not apply it to the practical context for lack of observations.

The East China Sea (ECS) boasts a vast continental shelf and strong tidal motions (Kang et al., 2002; Niwa and Hibiya, 2004). Many observations have been made to investigate the turbulence in this area (Liu et al., 2009; Lozovatsky et al., 2012, 2015; Song et al., 2019; Wang et al., 2020); however, these observations are still limited compared to the vastness of the ECS. Therefore, the investigation of tidal motions and turbulent mixing induced by tides in various regions is important and beneficial in deepening our understanding of the dynamics in the ECS. In this study, based on three records of the current velocity measured by acoustic Doppler current profilers (ADCPs) in the western ECS, we estimated the eddy viscosity profiles in the bottom Ekman boundary layer for two purposes. First, we need to assess the performance of the scheme proposed by Cao et al. (2017) in the real sea and compare it with the performance of other schemes. Second, we need to provide a turbulent mixing structure in the western ECS near Yangtze Estuary.

The paper is organized as follows. The observations and methods for estimating eddy viscosity are introduced in Section 2. In Section 3, characteristics of tidal currents and turbulence mixing induced by tides at three stations are presented. Section 4 summarizes the paper.

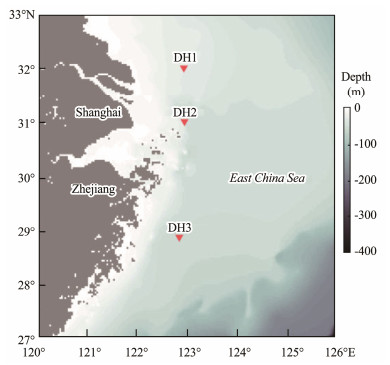
2 Data and Methods 2.1 Current Data

Current data of Wang et al. (2019) were used in this study. The data were measured using moored ADCPs at three stations (Fig.1): Station DH1 located at 122˚56.149΄E, 31˚59.803΄N, where the water depth is 34.3 m; Station DH2 at 122˚56.882΄E, 31˚01.450΄N, with a depth of 47.0 m; and Station DH3 at 122˚50.684΄E, 28˚54.826΄N, with a depth of 61.8 m. The ADCPs deployed at the three stations operated from June 12 to August 22, June 11 to September 4, and June 12 to October 20, 2014, respectively. All velocity profiles were collected every 30 minutes with a 2.0-m bin size. The first available bin of ADCP is 4.8 m above the bottom of the ocean.

2.2 Eddy Viscosity Estimation Schemes

The measured current velocity was used to estimate the eddy viscosity because the mean velocity profiles are determined by the mean turbulent mixing in the bottom boundary layer where the turbulent mixing term is dominant in the momentum equations. The governing equation for velocity in the bottom Ekman boundary layer is

$ \frac{{\partial w}}{{\partial t}} + {\text{i}}fw = \frac{\partial }{{\partial z}}\left[ {\mu (z)\frac{{\partial w}}{{\partial z}}} \right], $

(1)

where w = u + iv is the complex horizontal current vector, t is the time, f is the Coriolis frequency, z is the height above the seafloor, and μ is the eddy viscosity coefficient. Represent a tidal current of frequency ω by

$ w(z, t) = W(z)\exp ({\text{i}}\omega t) . $

(2)

According to Yoshikawa and Endoh (2015),

$ W(z) = \left\{ {\begin{array}{*{20}{l}} \begin{gathered} \frac{{{A_U}\cos {g_U} + {A_V}\sin {g_V}}}{2} + {\text{i}}\frac{{{A_V}\cos {g_V} - {A_U}\sin {g_U}}}{2}, \hfill \\ {\text{ }}\omega > 0 \hfill \\ \end{gathered} \\ \begin{gathered} \frac{{{A_U}\cos {g_U} - {A_V}\sin {g_V}}}{2} + {\text{i}}\frac{{{A_V}\cos {g_V} + {A_U}\sin {g_U}}}{2}, \hfill \\ {\text{ }}\omega < 0 \hfill \\ \end{gathered} \end{array}} \right., $

(3)

where ω > 0 corresponds to the counterclockwise-rotating current component and ω < 0 corresponds to the clockwise-rotating component; A_U (A_V) and g_U (g_V) are the conventional tidal harmonic coefficients of the zonal (meridional) velocities. If the tides are barotropic in the interior layer, the boundary layer component W(z) can be calculated as follows:

$ W(z) = \bar W(z) - \bar W(H + \delta), $

(4)

where $ \bar W(z) $ is the observed tidal current, H is the boundary layer height, and δ is an adjustment parameter set as a few meters to avoid errors in the eddy viscosity estimation near z = H. Substituting Eq. (2) in Eq. (1) yields

$ {\text{i}}(f + \omega)W(z) = \frac{\partial }{{\partial z}}\left[ {\mu (z)\frac{\partial }{{\partial z}}W(z)} \right] . $

(5)

The discretized form of Eq. (5) is

$\begin{align} {\text{i}}(f + {\omega _n}){W_{k + 1/2, n}}\Delta z = &{\mu _{k + 1}}\frac{{{W_{k + 3/2, n}} - {W_{k + 1/2, n}}}}{{\Delta z}} - \\& {\mu _k}\frac{{{W_{k + 1/2, n}} - {W_{k - 1/2, n}}}}{{\Delta z}}, \end{align}$

(6)

where n represents the tidal component (e.g., n = 1 is the clockwise component of the M₂ tide) and k is the vertical level. The first two schemes used to estimate the eddy viscosity are based on the above equation and the least squares method.

2.2.1 Scheme 1

Scheme 1 was first used by Yoshikawa et al. (2010). It assumes that errors are included in Eq. (6):

$\begin{align} {\text{i}}(f + {\omega _n}){W_{k + 1/2, n}}\Delta z = &{\mu _{k + 1}}\frac{{{W_{k + 3/2, n}} - {W_{k + 1/2, n}}}}{{\Delta z}} - \\& {\mu _k}\frac{{{W_{k + 1/2, n}} - {W_{k - 1/2, n}}}}{{\Delta z}} + {\varepsilon _{k, n}} . \end{align}$

(7)

Note that ε_{k, n} is a complex number. The sum of the squared ε_{k, n} is defined as

$ E = \sum\limits_{k, n} {{\varepsilon _{k, n}}\varepsilon _{k, n}^*}, $

(8)

where ^* denotes the complex conjugate. To minimize E, it is required that

$ \frac{1}{2}\frac{{\partial E}}{{\partial {\mu _k}}} = 0, \frac{1}{2}\frac{{\partial E}}{{\partial {\mu _k}}} = 0{\text{ }}(2 \leqslant k \leqslant K - 1), \frac{1}{2}\frac{{\partial E}}{{\partial {\mu _1}}} = 0 . $

(9)

The above equations are solved to obtain μ_k for all vertical levels.

2.2.2 Scheme 2

Scheme 2 was proposed by Yoshikawa and Endoh (2015). In this scheme, Eq. (6) is integrated from z_k to z_K = H, and the errors are assumed in the integrated equations:

$\begin{array}{l} \sum\limits_{k' = k}^{K - 1} {{\text{i}}(f + {\omega _n}){W_{k' + 1/2, n}}\Delta z} = {\mu _K}\frac{{{W_{K + 1/2, n}} - {W_{K - 1/2, n}}}}{{\Delta z}} - \\ \;\;\;\;\;\;\;\;\;\; {\mu _k}\frac{{{W_{k + 1/2, n}} - {W_{k - 1/2, n}}}}{{\Delta z}} + {\varepsilon _{k, n}} .\end{array} $

(10)

Taking partial derivatives of E with respect to μ_k and setting them equal to zero, μ_k can be obtained by solving the resulting equations:

$ \frac{1}{2}\frac{{\partial E}}{{\partial {\mu _K}}} = 0, \frac{1}{2}\frac{{\partial E}}{{\partial {\mu _k}}} = 0{\text{ }}(1 \leqslant k \leqslant K - 1) . $

(11)

2.2.3 Scheme 3

The third scheme used in the study is based on the adjoint method. Details can be found in Cao et al. (2017), and this scheme is also summarized as follows. The scheme is composed of the bottom Ekman boundary layer model and its adjoint model, as well as a minimization algorithm. The eddy viscosity profiles in the bottom Ekman boundary layer can be estimated by assimilating observations (harmonic constants of tidal currents).

The bottom Ekman boundary layer model is introduced above (Eqs. (1) – (6)).

The adjoint model development begins with the cost function calculation:

$ J = \sum\limits_n {\left[ {{\beta _n}\int {\frac{{{M_{{\text{obs}}}}}}{{\text{2}}}({W_n} - {{\hat W}_n}){{({W_n} - {{\hat W}_n})}^*}{\text{d}}z} } \right]}, $

(12)

where β_n is the weight coefficient, W_n is the simulated results of the bottom Ekman boundary layer model, $ {\hat W_n} $ is the observation, M_obs is the mask of observations (M_obs(z) = 1 represents observations at z that are assimilated into the model and M_obs(z) = 0 otherwise), and * denotes the conjugate.

The Lagrangian function is constructed as

$ L = J + \sum\limits_n {\left\{ {{\beta _n}\int {\lambda _n^*\left[ {{\text{i}}(f + {\omega _n}){W_n} - \frac{\partial }{{\partial z}}\left({\mu \frac{{\partial {W_n}}}{{\partial z}}} \right)} \right]{\text{d}}z} } \right\}}, $

(13)

where λ_n = λ_{r, n} + iλ_{i, n} is the complex adjoint variable of W_n.

The adjoint model is derived from $ \frac{{\partial L}}{{\partial {W_n}}} = 0 $:

$ \frac{\partial }{{\partial z}}\left({\mu \frac{{\partial \lambda _n^*}}{{\partial z}}} \right) - {\text{i}}(f + {\omega _n})\lambda _n^* = {M_{{\text{obs}}}}({W_n} - {\hat W_n}), $

(14)

with boundary conditions

$ \left\{ {\begin{array}{*{20}{l}} {\lambda _n^* = 0, {\text{ at }}z = Z} \\ {\lambda _n^* = 0, {\text{ at }}z = 0} \end{array}} \right. . $

Assuming that W_n is a single-valued function of μ, when the simulated W_n approaches the observation, the estimated μ should be close to its real value. Therefore, there exists a minimization problem, min: J(μ), which can be solved by adopting the gradient descent algorithm. The gradient of the cost function with respect to the eddy viscosity coefficient is

$ \frac{{\partial J}}{{\partial \mu }} = \sum\limits_n {\left[ {{\beta _n}{\rm{Re}} \left({\frac{{\partial \lambda _n^*}}{{\partial z}}\frac{{\partial {W_n}}}{{\partial z}}} \right)} \right]}, $

(15)

where Re indicates the real component. Considering that the eddy viscosity coefficients can vary by several orders of magnitudes in the bottom Ekman boundary layer, the gradient of the cost function with respect to the logarithm of the eddy viscosity coefficient is used in the minimization algorithm:

$ \frac{{\partial J}}{{\partial {{\log }_{10}}\mu }} = \mu \ln 10\frac{{\partial J}}{{\partial \mu }} = \mu \ln 10\sum\limits_n {\left[ {{\beta _n}{\rm{Re}} \left({\frac{{\partial \lambda _n^*}}{{\partial z}}\frac{{\partial {W_n}}}{{\partial z}}} \right)} \right]} . $

(16)

According to the gradient descent algorithm,

$ x_k^{t + 1} = x_k^t - {\alpha ^t}\nabla J(x_k^t), $

(17)

where x = log₁₀ μ, α is the step factor, and ∇J(x) denotes the gradient of J with respect to x, and t is the index of iteration steps. The initial value $ x_k^0 $ should be prescribed. To minimize J, the step factor is defined as

$ {\alpha ^t} = \frac{{{\alpha ^0}}}{{{{\left\| {\nabla J(x_k^t)} \right\|}_2}}}, $

(18)

where α₀ is a constant obtained through a trial-and-error procedure and $ {\left\| {\nabla J(x_k^t)} \right\|_2} $ is the L₂ norm of the gradient. After 1000 iterations, eddy viscosity coefficients μ are greatly optimized as the cost function decreases.

3 Results 3.1 Tidal Characteristics

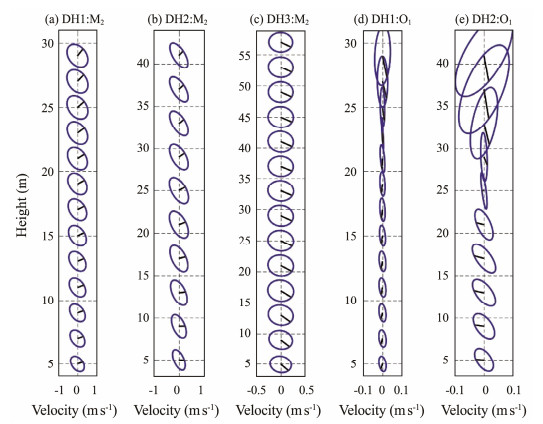
Harmonic analysis was first conducted on current velocity data to describe the characteristics of tides and to choose the tidal constitutes suitable for estimating the eddy viscosity. The t_tide toolbox (Pawlowicz et al., 2002) was applied to perform harmonic analysis (HA), which resolved 35 constituents based on the automated decision tree of Foreman (1977). Notably, only the M₂ and O₁ constituents were further analyzed according to the observing periods (for approximately 2 – 4 months). Additionally, the results of O₁ at DH3 were ignored because of their small magnitudes and relatively large confidence intervals. Fig.2 shows the vertical structures of the M₂ and O₁ tidal ellipses at the three stations. At first glance, we find that the M₂ tide is much stronger than the O₁ tide, which is consistent with previous studies (e.g., Kang et al., 1998; Fang et al., 2004). The M₂ tide is dominated by the barotropic component, displaying a uniform character throughout the water column except near the bottom, which is consistent with previous observations (Wang et al., 1999). The tidal ellipses at stations DH1 and DH2 are circular and aligned in the northwest-southeast directions. The M₂ tide at station DH3 is weaker than those at the other two stations and shows a more circular shape. The O₁ tide shows a different feature from the M₂ tide. The O₁ tides are surface intensified, and the variance of their Greenwich phase with depths is relatively large. The O₁ tide is more rectilinear compared to the M₂ tide. The major axis orientation of the O₁ tide at station DH1 is mainly north-south. At station DH2, the direction changes downward from northeast-southwest to northwest-southeast. In a word, the O₁ tides are much weaker and show more changes in the vertical direction.

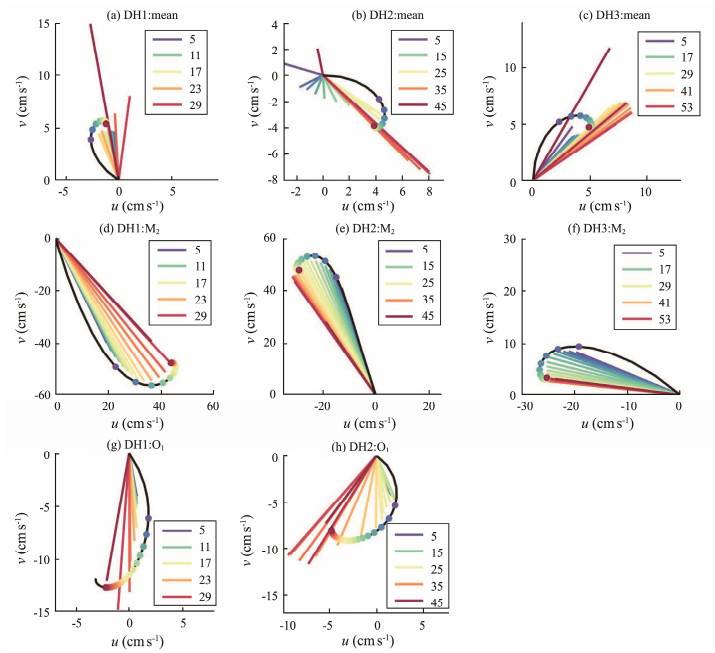
Fig.3 shows the vertical structures of the M₂, O₁, and mean currents (time average of the observed velocity during the entire period) at the three stations. The tidal velocity vector is displayed when the velocity at a 25-m height reaches its maximum. The classic Ekman solutions are also plotted for reference. They are calculated with a constant eddy viscosity of 10⁻³ m² s⁻¹ as follows:

$ \left\{ {\begin{array}{*{20}{l}} {w = W\exp ({\text{i}}\omega t)\left({1 - \exp \left({ - (1 + i)\frac{z}{{{\delta _E}}}} \right)} \right), {\text{ for }}f + \omega > 0} \\ {w = W\exp ({\text{i}}\omega t)\left({1 - \exp \left({ - (1 - i)\frac{z}{{{\delta _E}}}} \right)} \right), {\text{ for }}f + \omega < 0} \end{array}} \right., $

(19)

where

$ {\delta _E} = {\left({\frac{{2{\mu _0}}}{{\left| {f + \omega } \right|}}} \right)^{1/2}} . $

The features of the M₂ tidal currents are consistent with the classical Ekman theory in the bottom boundary layer. The currents rotate clockwise downward, and their magnitudes change slightly above around 20 m and decrease near the bottom. The O₁ tidal currents show a counterclockwise rotation with depth, which can be explained by the classical Ekman theory. However, their magnitude is much weaker than the M₂ tide and deviates further from the corresponding theoretical solution. The mean currents are also feeble, which are less than 5 cm s⁻¹ within 20 m height from the bottom. At stations DH1 and DH2, the mean current rotates clockwise with the increase of water depth, which is opposite to the direction predicted by the Ekman theory and can be attributed to small values (Yoshikwa et al., 2010). At station DH3, the rotation of the mean current is consistent with the theory.

3.2 Eddy Viscosity in the Bottom Boundary Layer

According to Yoshikawa and Endoh (2015) and Cao et al. (2017), the use of a stronger tidal constituent improves the eddy viscosity estimation. We use the M₂ tide to estimate the eddy viscosity because it is strong and shows a typical bottom Ekman spiral.

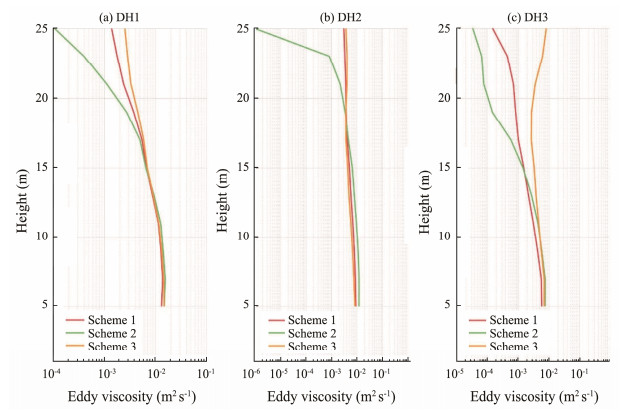
The boundary layer height, H, needs to be given a priori to calculate the Ekman boundary layer velocity. Although depths at the three stations vary from 30 to 60 m, the vertical structures of the M₂ tide in Figs.2 and 3 show that the velocity varies above the 20 m height, indicating that H at all these stations is similar. As suggested by Yoshikawa and Endoh (2015), we tried various values for H and set the top of the boundary layer at 25 m for all three stations. Fig.4 shows eddy viscosity profiles estimated from the three schemes at the ADCP stations. Overall, these profiles have a similar pattern – they show the maximum values at approximately 5 m height and decrease exponentially with the height (except that estimated by scheme 3 at EH3, which increases gradually above 20 m). The exponent decay rates are different because of various density profiles. At stations DH1 and DH2, results of the three schemes are close below the height of 20 m; however, near the top of the boundary layer, the eddy viscosity estimated by scheme 1 decreases to a value smaller than the other two schemes by 1 – 3 orders of magnitude. At station DH3, profiles estimated from the three schemes depart from each other above the height of 15 m, and their difference is larger compared to the other two stations. According to Yoshikawa and Endoh (2015), scheme 2 is susceptible to the balance error, which is relatively large in ADCP data observed in the ECS and which can account for the difference between estimation using scheme 2 and other schemes. The eddy viscosity profiles, even if estimated using the same schemes, differ at each station and from previous studies in the ECS (e.g., the first two schemes are used in Yoshikawa and Endoh (2015) to estimate eddy viscosity profiles at two stations in the ECS, the one located at 31˚45΄N, 127˚25΄E and the other at 31˚45΄N, 125˚30΄E), indicating that turbulence characteristics in the bottom boundary layer are site-independent and it is important to make more quantifications based on observations.

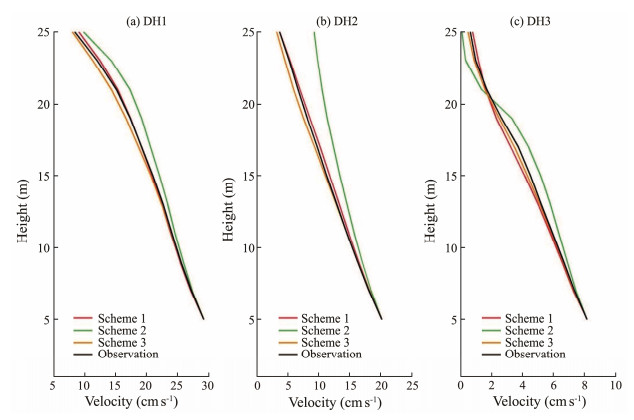
Velocity profiles were reproduced with the estimated eddy viscosity (according to Eq. (6)) and compared with the observations for validation because the true values of the eddy viscosity are unknown. The magnitudes of the M₂ tide are shown in Fig.5. All the reproduced velocities show a decreasing trend with height, which is similar to the observations. The profiles estimated with schemes 1 and 3 are much closer to the observations than those estimated with scheme 2. The depth-averaged root mean square of the errors of schemes 1 and 3 are smaller than that of scheme 2 by one order of magnitude at DH1 and DH2 (e.g., 0.27, 1.33, and 0.45 cm s⁻¹ for the three schemes, respectively, at DH1). At DH3, the error of scheme 2 is also the largest. The results indicate that the eddy viscosity profiles estimated from schemes 1 and 3 are close to the true values.

Based on the eddy viscosity estimated by scheme 3, the shear production of the turbulent kinetic energy of the M₂ and O₁ tides is calculated as follows:

$ SPR = \mu (z)\left({{{\left({\frac{{\partial u}}{{\partial z}}} \right)}^2} + {{\left({\frac{{\partial v}}{{\partial z}}} \right)}^2}} \right) . $

(20)

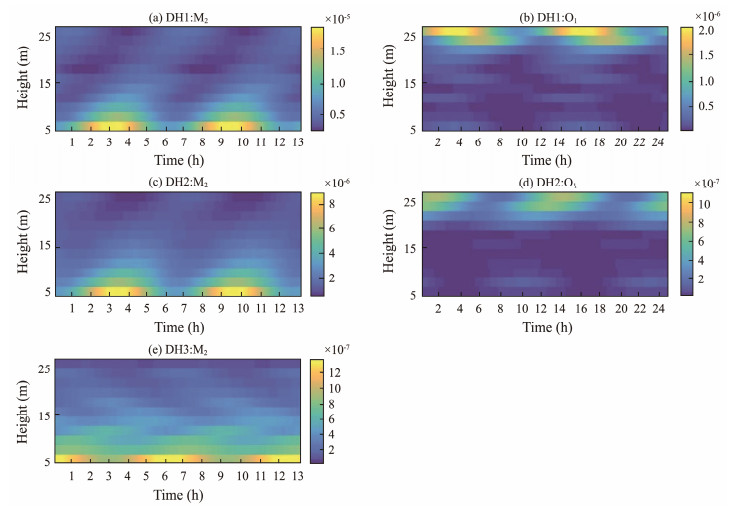
The results are displayed in Fig.6. Both show a periodic character, which is consistent with the corresponding tidal constituents. However, their characteristics are different from each other. In terms of magnitude, the M₂ shear production is larger than that of the O₁ tide by 1 order of magnitude at each station. In terms of the vertical structure, the M₂ shear production intensifies as it approaches the bottom, which is consistent with the theory of the bottom Ekman boundary layer. In contrast, the O₁ shear production is larger within the layer of height 20 – 25 m.

4 Summary

In this study, tidal characteristics at three stations in the ECS are analyzed, and the velocity profiles are used to estimate the eddy viscosity in the bottom boundary layer. The M₂ tide takes a dominant role and shows a barotropic feature, whereas the O₁ tide is much weaker and shows more changes in the vertical direction. Based on the M₂ tide, three schemes for estimating the eddy viscosity are compared. The results show that schemes 1 and 3 perform well in the western ECS near the Yangtze River. The estimated eddy viscosity shows the maximum values at approximately 5 m height and decreases exponentially with the height. The values vary within 10⁻⁴ – 10⁻² m² s⁻¹. Shear production of the turbulent kinetic energy of the M₂ and O₁ tides shows unique characteristics in terms of structure and magnitude. The shear production of the M₂ tide is much stronger than the diurnal tide and bottom intensified, whereas that of the O₁ tide shows larger values within the 15 – 25 m height range.

Acknowledgements

This study was supported by the Zhejiang Provincial Natural Science Foundation of China (No. LY21D060005), the Shandong Provincial Natural Science Foundation (No. ZR2022MD082), the Joint Project of Zhoushan Municipality and Zhejiang University (No. 2019C810060), the Open Fund Project of Key Laboratory of Marine Environmental Information Technology and the Strategic Priority Research Program of Chinese Academy of Sciences (No. XDA19060201).