2) Southern Offshore Wind Power Joint Development Co., Ltd., Zhuhai 519080, China;
3) Changjiang Survey Planning Design and Research Co., Ltd., Wuhan 430010, China
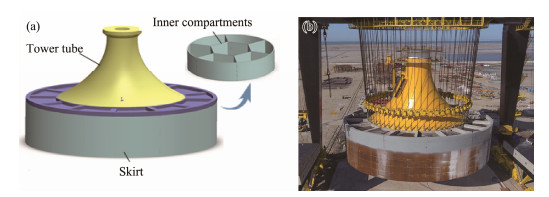
Offshore wind energy resources are globally abundant and it has great potential for the large-scale development of offshore wind power, but the construction of offshore wind farms continues to face many challenges (Dinh and Nguyen, 2019; Lee and Zhao, 2020). As a result of the complex marine environment and various structural forms of offshore wind turbines, wind turbine foundations bear an immense overturning load. Thus, a suitable foundation type is the key to controlling the uneven settlement of the foundation under the overturning load and ensuring the stability of the wind turbine. Considering the geological characteristics and hydrometeorological conditions of China, the team of wind power researchers from Tianjin University proposed a new type of bucket foundation with internal components (BFIC), which was successfully applied in Jiangsu's territorial waters (Ding et al., 2012; Lian et al., 2012; Zhang et al., 2013a, 2013b). The BFIC is a largediameter steel cylinder with one end closed (as shown in Fig.1). Its inner space is divided into several compartments by bulkheads to increase the stiffness of the foundation and enhance the levelling precision during installation. Unlike the traditional suction foundation, the diameter of a BFIC is usually greater than 30 m, and the embedment ratio generally does not exceed 0.5 (Liu et al., 2015). The wide and shallow structure of the foundation is conducive to resisting the tremendous overturning load generated by the superstructure, which effectively controls differential settlement and ensures the operational safety of the turbine.
|
Fig. 1 Bucket foundation with inner compartments. (a), schematic diagram; (b), photograph. |
The successful installation of the foundation is crucial. The installation of the bucket foundation can be divided into a self-weight sag stage and a suction installation stage. In the self-weight sag stage, the foundation first sinks into the seabed to a certain depth by its self-weight to reach the closed condition in the cylinder. During the subsequent suction installation stage, the foundation is penetrated to the design depth by the deviation pressure between the inside and outside of the skirt generated by pumping water and air. To ensure that the foundation can be smoothly installed, Mehravar et al. (2017) and Hu et al. (2018) discussed the seepage problem and estimated the required suction pressure during the installation of composite bucket foundations. Randolph and Tran (2008), Chen et al. (2016), Zhang et al. (2016), and Liu et al. (2019) carried out experimental researches on the penetration characteristics of bucket foundations in silt and sand and provided reasonable suggestion for calculating the penetration resistance. Houlsby and Byrne (2005) proposed a method to calculate the penetration resistance of bucket foundations in clay that involves the influence of suction on end resistance. Feld (2001), Senders and Randolph (2009), Ibsen and Thilsted (2011), and some other scholars calculated the critical pressure during the suction installation of bucket foundations in different soils and established the calculation formula of the critical pressure with depth. Notably, previous studies have promoted the application of bucket foundations in engineering. Nevertheless, the penetration characteristics of bucket foundations must be further investigated with the sustained development of engineering practice. Indeed, the installation of foundations is a complex engineering problem that requires the comprehensive consideration of various factors, such as subsidence resistance and critical pressure, and reasonably predicting the critical suction is crucial for the installation. Excessive suction causes seepage failure, buckling of the structure, and excessive soil plugs in the cylinder, whereas insufficient suction cannot overcome the penetration resistance of the foundation, and as a result, the bucket foundation cannot penetrate to the objective depth (Andersen et al., 2005; Leblanc et al., 2010). However, the calculations of critical suction in current studies are mostly based on soil seepage failure and soil plugs in the cylinder (Andersen et al., 2005; Houlsby and Byrne, 2005; Guo et al., 2012), whereas relatively few studies have investigated the buckling of a BFIC under critical suction.
In essence, a BFIC is a thin-walled, large-diameter cylindrical steel structure. Subjected to the deviation pressure between the internal and external parts of the skirt during the installation process, the skirt and bulkheads of the foundation are in danger of buckling failure; however, a reasonable evaluation method is limited. Hence, theoretical and numerical methods are used to calculate the critical buckling pressure of the skirt and bulkheads of the BFIC in this paper. Taking the BFIC of an offshore wind farm as an example, the buckling calculation results are compared with field survey data to verify the correctness of the calculation method.
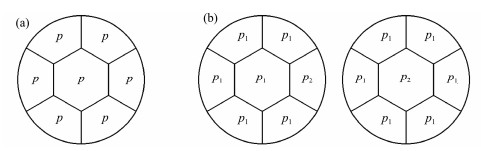
2 Theoretical Calculations of the Critical Buckling Pressure 2.1 Distribution of the Suction Pressure in the BucketThe buckling mode of the structure shows a close relation with the loading method. In the suction installation process, the bucket foundation may be under two working conditions according to the distribution of suction pressure: normal penetration and levelling. Under the normal penetration condition, the bucket foundation always maintains a horizontal state, and the suction pressure in each compartment is basically identical. Under the levelling condition, the inclination of the bucket foundation during penetration exceeds the limit due to the site flatness, soil strength distribution and other factors. Accurate levelling is required, which results in a deviation pressure between two adjacent compartments. The compartment pressure distributions of the bucket foundation under two working conditions are shown in Fig.2.
|
Fig. 2 Pressure distributions of the compartments. (a), normal penetration condition; (b), levelling condition. |
The variables p, p1, and p2 represent the cabin pressures, but p1 ≠ p2. The levelling condition includes the situations in which there is a deviation pressure between adjacent side compartments or between the side and the middle compartments. According to engineering experience, a lattice of various stiffeners is usually set on the lid of the bucket foundation to ensure that the lid has sufficient stiffness against the load transmitted by the upper tower. Therefore, it is reasonable to assume that the lid stiffness is sufficiently large to resist the buckling at least before the skirt and bulkheads. Therefore, it is only needed to calculate the critical buckling pressures of the skirt and bulkheads under the two conditions in Fig.2.
2.2 Normal Penetration Condition1) Buckling of the skirt
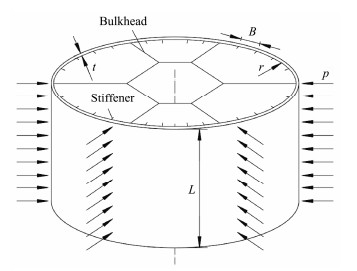
Under normal penetration conditions, the buckling calculation model for the critical pressure of the skirt can be simplified as an isotropic, cylindrical, thin-shelled structure of uniform material under a uniform load p, and its wall thickness t is much smaller than its radius r and length L, as shown in Fig.3. Based on the stability theory of a cylindrical shell, the stress at any point on the shell can be expressed by the axial design stress σa, d, hoop design stress σh, d, and tangential design shear stress τd. Under the uniformly distributed load p in the circumferential direction, assuming that the stress distribution inside the shell is constant along the thickness, the buckling design stress can be calculated as follow equation (DNVGL-RP-C202, 2018):
|
Fig. 3 Buckling calculation model of the skirt. |
| $ {\sigma _{\text{d}}}{\text{ = }}{\sigma _{{\text{h, d}}}}{\text{ = }}\frac{{pr}}{t}, $ | (1) |
where σd is the equivalent von Mises buckling design stress.
The cylindrical shell in Fig.3 is divided into n curved panels by bulkheads and longitudinal stiffeners, and the value of n depends on the number of bulkheads and stiffeners. Under a uniform load, the buckling stability of the curved panel is related to its aspect ratio. When the aspect ratio L/B > 1, the elastic buckling strength of the curved panel is affected mainly by the width B of the curved panel. When the aspect ratio L/B < 1, the curved panel can be considered a cylindrical shell structure with length L, and its elastic buckling strength is related mainly to the length L of the curved panel, as shown in Eq. (2) (DNVGL, 2018):
| $ {f_{{\text{Eh}}}} = \left\{ \begin{gathered} C\frac{{{{\text{π }}^2}E}}{{12\left({1 - {\upsilon ^2}} \right)}}{\left({\frac{t}{B}} \right)^2}\begin{array}{*{20}{c}} {}&{}&{{L \mathord{\left/ {\vphantom {L B}} \right. } B} > 1} \end{array} \hfill \\ C\frac{{{{\text{π }}^2}E}}{{12\left({1 - {\upsilon ^2}} \right)}}{\left({\frac{t}{L}} \right)^2}\begin{array}{*{20}{c}} {}&{}&{{L \mathord{\left/ {\vphantom {L B}} \right. } B} \leqslant 1} \end{array} \hfill \\ \end{gathered} \right., $ | (2) |
where fEh is the elastic buckling strength of the shell under circumferential loading, which is a function related to the size of the curved plate. The variables E and ν are the elastic modulus and Poisson's ratio of the material, respectively. C is the reduced buckling coefficient, which can be calculated according to Eq. (3):
| $ C = \psi \sqrt {1 + \frac{{\rho \xi }}{\psi }}, $ | (3) |
where ψ, ρ, and ξ are all calculation parameters, which can be determined from Table 1 according to the specifications (DNVGL-RP-C202, 2018).
|
|
Table 1 Calculation parameters |
According to Eq. (1) to Eq. (3), the critical buckling pressure of the skirt of the bucket foundation during the suction penetration can be calculated by Eq. (4).
| $ p = \frac{{{f_{{\text{Eh}}}}t}}{r} . $ | (4) |
2) Buckling of the bulkheads
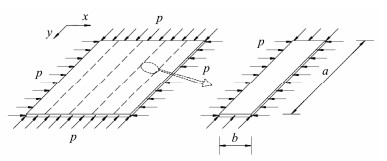
The buckling of bulkheads can be calculated based on the small deflection theory of thin plates. Under the normal penetration condition, although the pressures on both sides of the bulkhead neutralize each other because of the equal pressure of each compartment, the bulkhead is subjected to the load transmitted from the skirt, the lid, and the sidewall of the middle compartment. Therefore, the buckling analysis of the bulkheads can be simplified to the stability problem of simply supported thin plates under bidirectional compression, as shown in Fig.4, where a and b are the length and width, respectively, of the plate calculation unit.
|
Fig. 4 Simplified calculation model of the subdivided thin plate under the normal penetration condition. |
Since the wall thickness of the bulkhead is much smaller than its dimensions in the other two directions, the load p on the four sides of the bulkhead can be considered a linear load. The compressive stress on the four lateral sides of the plate caused by the linear load p can be expressed as:
| $ {\sigma _x} = {\sigma _y} = \frac{p}{t}, $ | (5) |
where σx and σy are the compressive stresses distributed along the length and width of the bulkhead, respectively.
The length of the midplane of the bulkhead is assumed to be unchanged under biaxial compressive stress. The differential governing equation and boundary conditions for the buckling of the bulkhead can be derived based on the bending equilibrium equation, which is expressed by Eq. (6):
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{D}{t}{\nabla ^4}w + {\sigma _x}\frac{{{\partial ^2}w}}{{\partial {x^2}}} + {\sigma _y}\frac{{{\partial ^2}w}}{{\partial {y^2}}} = 0} \\ {x = 0{\text{, }}a{\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} w = 0;{\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\partial ^2}w}}{{\partial {x^2}}} = 0} \\ {y = 0{\text{, }}b;{\kern 1pt} {\kern 1pt} {\kern 1pt} w = 0;{\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\partial ^2}w}}{{\partial {y^2}}} = 0} \end{array}} \right., $ | (6) |
where D is the bending stiffness of the bulkhead, D = Et3/12(1 − υ2); w is the deflection of the bulkhead; and ∇ is the Laplace operator.
The solution of Eq. (6) conforming to the corresponding boundary conditions can be expressed by the double trigonometric series in Eq. (7) (Timoshenko and Gere, 2009):
| $ w = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{A_{mn}}\sin \frac{{m\pi x}}{a}\sin \frac{{n\pi y}}{b}} }, $ | (7) |
where Amn is the undetermined coefficient and m and n are the half wavenumbers along the length and width directions, respectively, when the bulkhead is unstable.
Substituting Eq. (7) into Eq. (6):
| $ \frac{D}{t}\sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{A_{mn}}\sin \frac{{m{\text{π }}x}}{a}\sin \frac{{n{\text{π }}y}}{b}\left[ {{{\left({\frac{{m{\text{π }}}}{a}} \right)}^4} + {{\left({\frac{{n{\text{π }}}}{b}} \right)}^4}} \right.} } $ |
| $ \left. { + 2{{\left({\frac{{m\pi }}{a}} \right)}^2}{{\left({\frac{{n\pi }}{b}} \right)}^2} - {\sigma _x}{{\left({\frac{{m\pi }}{a}} \right)}^2} - {\sigma _y}{{\left({\frac{{n\pi }}{b}} \right)}^2}} \right] = 0 . $ | (8) |
In the above equation, both sin(mπx/a) and sin(nπy/b) cannot be zero, and Amn is not zero; otherwise, the plate still holds a plane at the equilibrium state. As a result, Eq. (8) can be further simplified:
| $ D{\left[ {{{\left({\frac{m}{a}} \right)}^2} + {{\left({\frac{n}{b}} \right)}^2}} \right]^2}{\text{ = }}\frac{t}{{{{\text{π }}^2}}}\left[ {{\sigma _x}{{\left({\frac{m}{a}} \right)}^2} + {\sigma _y}{{\left({\frac{n}{b}} \right)}^2}} \right] . $ | (9) |
Introducing the dimensionless quantity φ = a/b and solving Eq. (9), the critical pressure can be calculated as:
| $ {p_{{\text{cr}}}} = {\sigma _{x, {\text{cr}}}}t = K\frac{{{{\text{π }}^2}D}}{{{b^2}}}, $ | (10) |
where K is the buckling coefficient, K = (m/φ)2 + n2.
Obviously, Eq. (10) shows that the critical buckling pressure of the bulkhead is related to its size. For the buckling coefficient K, the half wavenumbers m and n are positive integers when the plate is unstable. In addition, Eq. (10) can be used to calculate the minimum critical buckling pressure of the bulkhead when m and n are taken as 1.
2.3 Levelling Condition1) Buckling of the skirt
According to the above analysis, the capacity of the skirt to resist buckling is related to its size and material properties and is unrelated to the form of the pressure distribution. Therefore, the same theoretical calculation method as the normal penetration condition can be used to calculate the critical buckling pressure of the skirt.
2) Buckling of the bulkheads
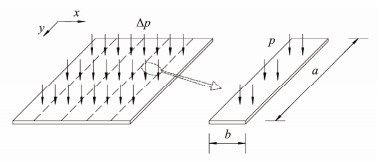
Under the levelling condition in Fig.2, the bulkhead bears the uniformly distributed pressure perpendicular to the plate surface. In this case, the buckling analysis of a bulkhead can be considered as a bending problem under uniformly distributed pressure, which also belongs to the category of small deflection theory. If the bulkhead has stiffeners, they can be considered as simple support constraints, and the thin plate separated by stiffeners is used for analysis, as shown in Fig.5, where Δp is the deviation pressure between two adjacent compartments: Δp = p1 − p2.
|
Fig. 5 Simplified calculation model of the subdivided thin plate under the levelling condition. |
The differential governing equation for the bending problem of the bulkhead in Fig.5 is established, and its boundary conditions under simple supports on four sides are defined, as shown in Eq. (11).
| $ \left\{ {\begin{array}{*{20}{l}} {D\left({\frac{{{\partial ^4}w}}{{\partial {x^4}}} + 2\frac{{{\partial ^4}w}}{{\partial {x^2}\partial {y^2}}} + \frac{{{\partial ^4}w}}{{\partial {y^4}}}} \right) = \Delta p} \\ {x = 0{\text{, }}a{\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} w = 0;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\partial ^2}w}}{{\partial {x^2}}} = 0} \\ {y = 0{\text{, }}b;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} w = 0;{\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\partial ^2}w}}{{\partial {y^2}}} = 0} \end{array}} \right.. $ | (11) |
Eq. (11) is obviously similar to Eq. (6), so it can also be solved by the double trigonometric series method. In addition, the solution of Eq. (7) satisfies Eq. (11); the load Δp is also expanded by a double trigonometric series:
| $ \Delta p = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{a_{mn}}\sin \frac{{m\pi x}}{a}\sin \frac{{n\pi y}}{b}} }, $ | (12) |
where amn is an undetermined coefficient that must be determined according to subsequent derivation. m and n take only odd terms (1, 3, 5,…) because the load Δp is symmetric about x = a/2 and y = b/2. According to the orthogonality of the trigonometric series, both ends of Eq. (12) are multiplied by
| $ \int_0^a {\int_0^b {\Delta p\sin \frac{{m\pi x}}{a}\sin \frac{{n{\text{π }}y}}{b}{\kern 1pt} } {\text{d}}x{\text{d}}y = \frac{{ab}}{4}{a_{mn}}} . $ | (13) |
The load Δp in the above equation is constant, so the coefficient amn can be simplified as:
| $ {a_{mn}}{\text{ = }}\frac{{4\Delta p}}{{ab}}\int_0^a {\int_0^b {\sin \frac{{m{\text{π }}x}}{a}\sin \frac{{n{\text{π }}y}}{b}{\kern 1pt} } {\text{d}}y{\text{d}}x = } \frac{{16\Delta p}}{{{{\text{π }}^2}mn}} . $ | (14) |
Substituting Eq. (7) and Eq. (12) into Eq. (11), the equation at any point (x, y) on the plate should always be established. For this purpose, each term of the triangular coefficients should be equal; thus, the coefficient Amn is:
| $ {A_{mn}}{\text{ = }}\frac{1}{{{{\text{π }}^4}D}} \cdot \frac{{{a_{mn}}}}{{{{\left({{{{m^2}} \mathord{\left/ {\vphantom {{{m^2}} {{a^2}}}} \right. } {{a^2}}} + {{{n^2}} \mathord{\left/ {\vphantom {{{n^2}} {{b^2}}}} \right. } {{b^2}}}} \right)}^2}}} . $ | (15) |
With the coefficient Amn, Eq. (7) can be solved. The solution of the equation is the general solution of the deflection of the four-sided simply supported plate under a lateral uniformly distributed load.
| $ w = \frac{{16\Delta p}}{{{{\text{π }}^6}D}}\sum\limits_{m = 1}^¥ {\sum\limits_{n = 1}^¥ {\frac{{\sin \frac{{m{\text{π }}x}}{a}\sin \frac{{n{\text{π }}y}}{b}}}{{mn{{\left({{{{m^2}} \mathord{\left/ {\vphantom {{{m^2}} {{a^2}}}} \right. } {{a^2}}} + {{{n^2}} \mathord{\left/ {\vphantom {{{n^2}} {{b^2}}}} \right. } {{b^2}}}} \right)}^2}}}} } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left({m{\text{, }}n = 1, 3, 5, \cdot \cdot \cdot } \right) . $ | (16) |
Evidently, the maximum deflection of the plate under a uniform load occurs at the centre point (x = a/2, y = b/2). Since the trigonometric series of Eq. (16) converges quickly, only the first term (m = 1, n = 1) of the trigonometric series can satisfy the calculation requirements. According to the small deflection theory of a thin plate, the maximum deflection of the plate does not exceed 1/5 of the thickness (Timoshenko and Woinowsky-Krieger, 1959), as shown in Eq. (17).
| $ w = \frac{{16\Delta p}}{{{{\text{π }}^6}D{{\left({{1 \mathord{\left/ {\vphantom {1 {{a^2}}}} \right. } {{a^2}}} + {1 \mathord{\left/ {\vphantom {1 {{b^2}}}} \right. } {{b^2}}}} \right)}^2}}} \leqslant \frac{t}{5} . $ | (17) |
Hence, the critical pressure of the plate is also related to its own size, which can be calculated by Eq. (18).
| $ \Delta p = \frac{{{{\text{π }}^6}Dt{{\left({{1 \mathord{\left/ {\vphantom {1 {{a^2}}}} \right. } {{a^2}}} + {1 \mathord{\left/ {\vphantom {1 {{b^2}}}} \right. } {{b^2}}}} \right)}^2}}}{{80}} . $ | (18) |
Based on the stability theory of cylindrical shells and the small deflection theory of thin plates, the critical buckling deviation pressures for skirts and bulkheads of bucket foundations are calculated. Although the proposed calculated formulas are relatively simple and convenient, the boundary conditions of the foundation and load are simplified in the formula derivation, and the rationality of the formulas must be verified. The finite element method can be used to intuitively analyze the buckling mode of the structure and mutually verify the theoretical settlement results. Therefore, the finite element analysis method is used to calculate the critical buckling differential pressure of the bucket foundation.
3 Numerical Analyses of the Critical Buckling PressureThe core of the numerical analysis is to calculate the critical buckling pressure of the bucket foundation by the Buckle analysis step in the commercial finite element software ABAQUS. Buckle analysis, which is also known as eigenvalue buckling analysis, is a linear buckling analysis method that can automatically find the most likely buckling behaviour according to the eigenvalues. Usually, the product of the first-order eigenvalue and applied load is taken as the critical buckling pressure of the foundation. Therefore, the numerical analysis results no longer distinguish the buckling of the skirt and bulkheads, which is the most dangerous situation in the buckling of the skirt and bulkheads. Thus, when the numerical analysis method is used to calculate the critical buckling pressure of a bucket foundation, it is necessary to consider the normal penetration and levelling conditions in Fig.2.
At present, the most commonly used numerical analysis model is a simplified buckling calculation model, ignoring the interaction between the foundation and the soil. To overcome this shortcoming, a new buckling calculation model involving the skirt-soil interaction is proposed. The specific modelling process of the two models is described as follows.
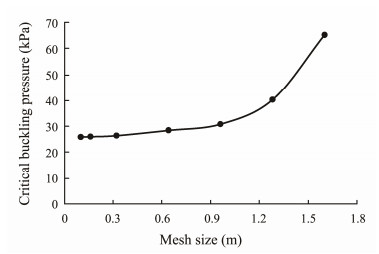
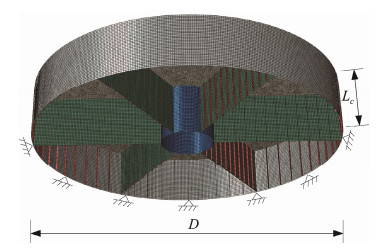
3.1 Simplified Buckling Calculation ModelThe simplified buckling calculation model is established only for the part of the foundation above the mud surface by shell elements and assumes the bottom of the model as a fixed boundary. In the model, the bucket foundation is set as a linear elastic constitutive structure with an elastic modulus of 210 GPa and a Poisson's ratio of 0.3. The height of the simplified model, Lc, is equal to the height of the foundation above the mudline. The load of the simplified model is set as a unit load, and the load distribution is identical to the actual situation. A fixed constraint is imposed on the bottom of the model, and a four-node curved shell element (S4R) is used for meshing. To avoid the influence of element size on the calculation results, a sensitivity analysis of the mesh size is carried out, and the results are shown in Fig.6. The results reveal that the minimum mesh size is 0.16 m, which is 0.005D. According to the determined meshing strategy, the simplified buckling calculation model of the bucket foundation is established, as shown in Fig.7.
|
Fig. 6 Sensitivity analysis of the mesh size. |
|
Fig. 7 Simplified buckling calculation model. |
In the above simplified eigenvalue algorithm, the skirtsoil interaction is simplified as a fixed constraint. However, the embedding effect of soil on the bucket foundation increases with the penetration depth. It is possible to be equivalent to the fixed constraint only when the penetration depth of the bucket foundation is sufficient. In conclusion, although the simplified eigenvalue algorithm is simple for calculating, there is a risk of overestimating the critical buckling pressure. The skirt-soil interaction should be considered in the numerical analysis of the critical buckling pressure of the bucket foundation.
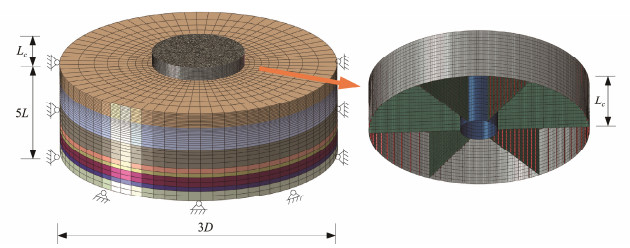
Therefore, a finite element calculation model considering the skirt-soil interaction is established. The soil is modelled by the solid element, which is an ideal elastic-plastic material and obeys the Mohr-Coulomb yield criterion. The diameter of the soil calculation area is 3D, and the depth is 5L to ensure that the results are independent of the boundaries. The shell element is still used for the bucket foundation, and the material properties are identical to those of the simplified buckling calculation model. The skirt-soil interaction is modelled by a surface-to-surface contact in Abaqus. The normal behaviour of the interface does not limit the transmission of contact pressure, but the contact surface is allowed to freely separate when the normal contact pressure drops to zero. The interface tangential behaviour follows the Mohr-Coulomb friction criterion, and the roughness coefficient of the contact surface is generally taken as 0.1 – 0.5 (Coffman, 2004; Vasquez et al., 2010). The solid element in the model is meshed by the three-dimensional eight-node reduced integral element (C3D8R). The mesh is densified near the bucket foundation with a size of 0.016 m. Moreover, the shell element is meshed by the fournode curved shell element (S4R). The zero-displacement boundaries of the model are located at the outside and bottom of the model. In the calculation, the geostatic stress is first applied to the soil; then, the buckling analysis step is carried out. The established finite element model considering the skirt-soil interaction is shown in Fig.8.
|
Fig. 8 Buckling calculation model considering the skirt-soil interaction. |
These two models can be used to calculate the critical buckling pressure of bucket foundations under normal penetration conditions and levelling conditions, but the advantages and disadvantages of the two models must be evaluated in combination with the calculation results of specific projects.
4 Analysis of an Engineering Case 4.1 Project Overview and Pre-Analysis1 BFIC design scheme
A BFIC was selected as the foundation of the wind turbine in an offshore wind farm in Jiangsu Province. The diameter D and embedment L of the BFIC are 32 m and 7 m, respectively; the lid thickness t1 = 30 mm, and the skirt thickness t2 = 20 mm. The inner space of the BFIC is divided into 7 compartments by bulkheads, of which themiddle compartment is cylindrical with diameter d = 5.5 m and wall thickness t3 = 20 mm. The middle com partment penetrates the lid and is connected to the upper tower. The other compartments are evenly distributed around the middle compartment, and the thickness of each bulkhead t4 = 20 mm. In addition, the skirt and bulkheads are also designed with longitudinal stiffeners, which are arranged at an interval of 6° on the skirt and at equal intervals on the bulkhead (11 stiffeners for each bulkhead). For convenience, the compartments are numbered in clockwise order, of which the 1st is the middle compartment and the 2nd – 7th are the side compartments. The compartment distribution of the BFIC is shown in Fig.9. The soil layer parameters of the site are shown in Table 2.
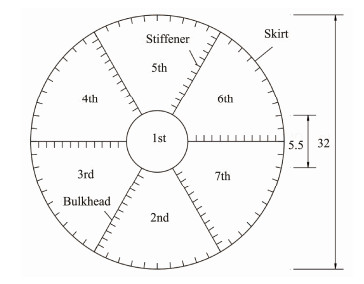
|
Fig. 9 Compartment distribution of the BFIC (m). |
|
|
Table 2 Soil layer parameters |
2 Pre-analysis of the critical buckling pressure
1) Theoretical analysis
The critical buckling pressures of the skirt and bulkheads of the BFIC under normal penetration conditions and levelling conditions are calculated by Eq. (4), Eq. (10) and Eq. (18), and the results are shown in Fig.10. As the calculation methods for the critical buckling pressure of the skirt are identical under normal penetration conditions and levelling conditions, the buckling calculation results of the skirt are shown in Fig.10 with only one solid line.
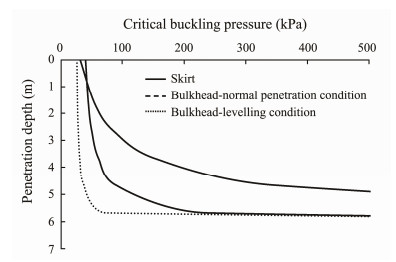
|
Fig. 10 Theoretical calculation results of the critical buckling pressures. |
Fig.10 shows that the critical buckling pressures of both the skirt and the bulkhead highly correlate with the penetration depth of the BFIC, mainly because the embedding effect is enhanced significantly with the increasing penetration depth. However, the decreasing height of the BFIC above the mudline also tremendously improves the geometric characteristics of the skirt and bulkhead, which increases the critical bucking pressures. Under normal penetration conditions, the critical buckling pressure of the bulkhead is obviously greater than the critical buckling pressure of the skirt, indicating that the skirt may buckle before the bulkhead in the process of suction penetration. Under the levelling condition, the premise for the bending instability of the bulkhead under the critical differential pressure is that the pressures p1 and p2 do not cause buckling of the skirt and bidirectional compression instability of the bulkhead.
2) Numerical analysis
The critical buckling pressure of the BFIC is also calculated by the simplified buckling calculation model and the buckling calculation model involving the skirt-soil interaction. In the second model, the soil parameters are set according to Table 2, and the friction coefficient of the skirtsoil interface is set to 0.35. The buckling modes of the BFIC calculated by these two models are shown in Fig.11, and the variable U represents the deformation caused by unit load.
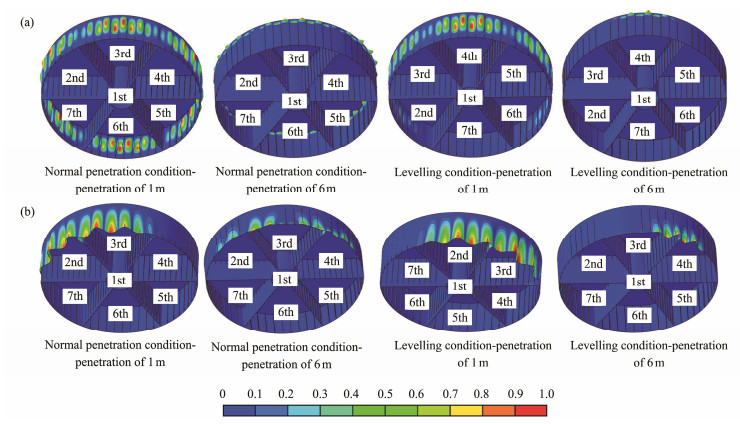
|
Fig. 11 Buckling modes of the numerical calculation. (a), simplified buckling calculation model; (b), buckling calculation model considering the skirt-soil interaction. |
Comparing the buckling modes of the two models in Fig.11, the buckling modes of the simplified calculation model under normal penetration conditions are symmetrical, and buckling occurs only in the part of the BFIC above the mudline, which is related to the simplified boundary conditions in the model. For the case of a large deviation pressure between adjacent compartments under levelling conditions, the buckling mode is not symmetrical and buckling generally occurs in the opposite compartment with a significant difference in pressures. For the model considering the skirt-soil interaction, the buckling modes under all conditions show asymmetry, but the buckling generally develops upwards from the bottom of the BFIC, mainly because the embedment effect of the soil is relatively weak compared with the great stiffness of the lid. As a result, buckling develops upwards from the end of the BFIC, even if the buckling position may have been embedded in the soil.
The critical buckling pressures of the BFIC calculated by the finite element method under different conditions are extracted, as shown in Fig.12.
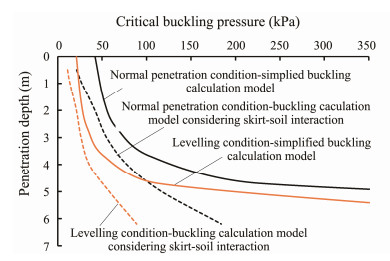
|
Fig. 12 Numerical results of the critical buckling pressure. |
Fig.12 shows that the critical buckling pressure of the BFIC increases with depth under both conditions, which has a trend similar to the theoretical results. The critical buckling pressure in the simplified buckling calculation model results higher than that in the model considering the skirtsoil interaction under the same penetration depth because the simplified buckling calculation model ignores the skirtsoil interaction. Therefore, during the suction installation process of the BFIC, to ensure the safety of the construction, it is necessary to control the suction and differential pressure not to exceed the limit obtained from the buckling calculation model considering the skirt-soil interaction shown in Fig.12. Most importantly, when selecting the finite element method to calculate for similar projects, the skirtsoil interaction should be involved in the buckling calculation model.
4.2 Comparison Between the Calculation Results and Monitoring DataAccording to the feedback from the construction site, the BFIC was smoothly installed. The monitoring data of compartment pressure are compared with the theoretical and numerical calculation results, as shown in Fig.13. The monitoring data show that the suction installation began from a penetration depth of 1.7 m, and the pressures in all compartments simultaneously continuously increased until the penetration depth was 5 m. During the installation process, due to levelling, the differential pressures of the 2nd – 3rd compartments and the 3rd – 4th compartments were maintained at approximately 20 kPa. There was no drastic change in the pressure of each compartment, which indicates that there was no rapid variation in the penetrated resistance of the BFIC. Based on this observation, the BFIC did not buckle.
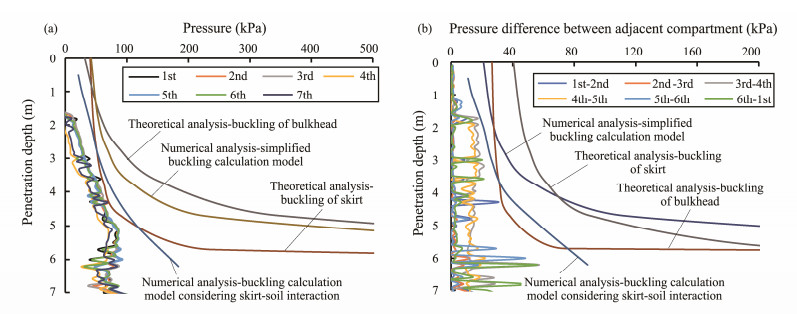
|
Fig. 13 Comparison between the calculated results and measured data. (a), normal penetration condition; (b), levelling condition. |
Fig.13a shows that the measured pressure of each compartment is basically within the critical buckling pressure line of the BFIC obtained by the theoretical and numerical methods, which indicates that the foundation will not buckle under normal penetration conditions. According to the results in Fig.13b, the deviation pressure between adjacent compartments of the BFIC is also completely within the critical buckling deviation pressure line calculated by the theoretical and numerical algorithm, which indicates that the BFIC will not buckle under the levelling condition. The comparison between the calculated results and measured data under all conditions show that the skirt and bulkheads will not buckle during the foundation installation, which is completely consistent with the non-buckling situation of the BFIC in practical engineering. Thus, the theoretical and numerical methods proposed in this paper are reasonable and can be used to calculate the critical buckling pressure of bucket foundations in engineering.
5 ConclusionsThe control of the critical buckling pressure of bucket foundations is an important part of foundation design. In this paper, theoretical and numerical methods are used to calculate the critical buckling pressure during the suction installation of a BFIC, and the calculation method is verified based on practical engineering data. The main conclusions are summarized as follows:
1) Theoretical calculation methods for the critical buckling pressures of the skirt and bulkheads in a BFIC are proposed. The results show that the skirt of a BFIC is more likely to prone to buckling than the bulkhead, while the pressure distributes uniformly in the compartments.
2) A buckling calculation model considering the skirtsoil interaction is proposed. The analysis to an engineering example shows that the critical buckling pressure of the buckling calculation model considering the skirt-soil interaction is significantly lower than that of the simplified buckling calculation model. Therefore, when the numerical analysis method is used in similar projects, the buckling calculation model considering the skirt-soil interaction should be recommended.
3) The field monitoring data verified the rationality of the theoretical methods and recommended numerical analysis model. The two methods have different advantages: the theoretical method is simple to calculate, but the recommended numerical calculation model can obtain the buckling mode of the foundation. Thus, the two methods can be flexibly and cooperatively used in practical engineering.
AcknowledgementThe authors are grateful for the support provided by the National Natural Science Foundation for Distinguished Young Scholars of China (No. 51825904).
Andersen, K. H., Murff, J. D., Randolph, M. F., Clukey, E. C., Erbrich, C. D., Jostad, H. P., et al., 2005. Suction anchors for deepwater applications. Proceedings of the International Symposium on Frontiers in Offshore Geotechnics. Perth, 3-30.
(  0) 0) |
Chen, F., Lian, J. J., Wang, H. J., Liu, F., Wang, H. Z., and Zhao, Y., 2016. Large-scale experimental investigation of the installation of suction caissons in silt sand. Applied Ocean Research, 60: 109-120. DOI:10.1016/j.apor.2016.09.004 (  0) 0) |
Coffman, R. A., El-Sherbiny, R. M., Rauch, A. F., and Olson, R. E., 2004. Measured horizontal capacity of suction caissons. Proceedings of the Offshore Technology Conference. Houston, 16161.
(  0) 0) |
Ding, H. Y., Li, Z. Z., Lian, J. J., and Huang, X., 2012. Soil reinforcement experiment inside large-scale bucket foundation in muddy soil. Transactions of Tianjin University, 18(3): 168-172. DOI:10.1007/s12209-012-1657-1 (  0) 0) |
Dinh, V. N., and Nguyen, H. X., 2019. Design of an offshore wind farm layout. Proceedings of the 1st Vietnam Symposium on Advances in Offshore Engineering. Hanoi, 233-238.
(  0) 0) |
DNVGL-RP-C202, 2018. Buckling Strength of Shells. Det Norske Veritas, Oslo, 13-22.
(  0) 0) |
Feld, T., 2001. Suction buckets, a new innovative foundation concept, applied to offshore wind turbines. PhD thesis. Aalborg University.
(  0) 0) |
Guo, Z., Wang, L. Z., Yuan, F., and Li, L. L., 2012. Model tests on installation techniques of suction caissons in a soft clay seabed. Applied Ocean Research, 34: 116-125. DOI:10.1016/j.apor.2011.09.004 (  0) 0) |
Houlsby, G. T., and Byrne, B. W., 2005. Design procedures for installation of suction caissons in clay and other materials. Geotechnical Engineering, 158(GE2): 75-82. (  0) 0) |
Hu, R. Q., Zhang, P. Y., Ding, H. Y., and Le, C. H., 2018. Numerical analysis of seepage field of bucket foundations for offshore wind turbines. Ships and Offshore Structures, 13(8): 822-834. DOI:10.1080/17445302.2018.1464892 (  0) 0) |
Ibsen, L. B., and Thilsted, C. L., 2011. Numerical study of piping limits for suction installation of offshore skirted foundations and anchors in layered sand. Proceedings of International Symposium on Frontiers in Offshore Geotechnics. Perth, 421-426.
(  0) 0) |
LeBlanc, C., Ahle, K., Nielsen, S. A., and Ibsen, L. B., 2010. The monopod bucket foundation: Recent experience and challenges ahead. The European Offshore Wind Conference & Exhibition. Stockholm, 1-5.
(  0) 0) |
Lee, J., and Zhao, F., 2020. Global offshore wind report 2020. Global Wind Energy Council, Brussels, 5-8.
(  0) 0) |
Lian, J. J., Ding, H. Y., Zhang, P. Y., and Rui, Y., 2012. Design of large-scale prestressing bucket foundation for offshore wind turbines. Transactions of Tianjin University, 18(2): 79-84. DOI:10.1007/s12209-012-1661-5 (  0) 0) |
Liu, R., Chen, G. S., Lian, J. J., and Ding, H. Y., 2015. Vertical bearing behaviour of the composite bucket shallow foundation of offshore wind turbines. Journal of Renewable & Sustainable Energy, 7(1): 717-728. (  0) 0) |
Liu, R., Ma, W. G., Qi, Y., and Wu, X. L., 2019. Experimental studies on the drag reduction effect of bucket foundation installation under suction pressure in sand. Ships and Offshore Structures, 14(5): 421-431. DOI:10.1080/17445302.2018.1500188 (  0) 0) |
Mehravar, M., Harireche, O., Faramarzi, A., and Alani, A. M., 2017. Modelling the variation of suction pressure during caisson installation in sand using FLAC3D. Ships and Offshore Structures, 12(7): 893-899. DOI:10.1080/17445302.2015.1051311 (  0) 0) |
Randolph, M. F., and Tran, M. N., 2008. Variation of suction pressure during caisson installation in sand. Géotechnique, 58(1): 1-11. DOI:10.1680/geot.2008.58.1.1 (  0) 0) |
Senders, M., and Randolph, M. F., 2009. CPT-based method for the installation of suction caissons in sand. Journal of Geotechnical and Geoenvironmental Engineering, 135(1): 14-25. DOI:10.1061/(ASCE)1090-0241(2009)135:1(14) (  0) 0) |
Timoshenko, S. P., and Gere, J. M., 2009. Theory of Elastic Stability. 2nd edition. Dover Publications, New York, 560pp.
(  0) 0) |
Timoshenko, S., and Woinowsky-Krieger, S., 1959. Theory of Plates and Shells. 2nd edition. McGraw-Hill Book Company, New York, 560pp.
(  0) 0) |
Vasquez, L. F. G., Maniar, D. R., and Tassoulas, J. L., 2010. Installation and axial pullout of suction caissons: Numerical modeling. Journal of Geotechnical & Geoenvironmental Engineering, 136(8): 1137-1147. (  0) 0) |
Zhang, P. Y., Ding, H. Y., Le, C. H., and Huang, X., 2013a. Motion analysis on integrated transportation technique for offshore wind turbines. Journal of Renewable and Sustainable Energy, 5(5): 053117. DOI:10.1063/1.4822056 (  0) 0) |
Zhang, P. Y., Ding, H. Y., Zhai, S. H., and Xiong, K. P., 2013b. Test on muddy soil reinforcement by negative pressure and electroosmosis inside cover-bearing-type bucket foundation for offshore wind turbines. Transactions of Tianjin University, 19(1): 10-16. DOI:10.1007/s12209-013-2069-6 (  0) 0) |
Zhang, P. Y., Zhang, Z., Liu, Y. G., and Ding, H. Y., 2016. Experimental study on installation of composite bucket foundations for offshore wind turbines in silty sand. Journal of Offshore Mechanics and Arctic Engineering, 138: 061901-1. DOI:10.1115/1.4034456 (  0) 0) |
 2023, Vol. 22
2023, Vol. 22


