2) State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics, The Chinese Academy of Sciences, Beijing 100029, China;
3) Shandong Provincial Key Laboratory of Ocean Engineering, Ocean University of China, Qingdao 266100, China
The rational evaluation and utilization of wave energy resources will positively contribute to easing the energy crisis (Esteban et al., 2019; Rodriguez-Delgado et al., 2019). Akpinar and Kömürcü (2013) performed an in-depth numerical simulation analysis with high temporal-spatial resolution on the wave energy of the Black Sea using the Simulating WAves Nearshore (SWAN) wave model. The southwest coasts of the Black Sea were found to be the best for installing a wave farm. In 2017, Akpinar et al. (2017) presented a long-term analysis of wave energy in the Black Sea based on a 31-year hindcast. Their results indicated that areas with the highest wave energy are in the southwestern part of the Black Sea, i.e., the Burgas-Rezovo area (43.9 MW hm−1), followed by the Dolni Chiflik-Shkorpilovtsi (37.3 MW hm−1) and the Istanbul-Alacali (36.1 MW hm−1) regions. Akpinar and Bingölbali (2016) and Akpinar and Ponce de Leon (2016) also conducted research on wind and wave conditions, which can be used as reference for ensuring environmental security for wave energy development. Kamranzad et al.(2015, 2016) used two 30-year SWAN wave models to pioneer the evaluation of wave energy in the Gulf of Oman and Persian Gulf, which filled a research gap in this area. Relatively stable wave conditions were found in this region. Liang et al. (2013) and Yan et al. (2019) provided an important and detailed reference regarding wave energy utilization in the seas around China. In addition, a relative energy-rich area was identified in the South China Sea (SCS). Rusu et al. (2018) and Rusu (2019) jointly evaluated the wave and wind energies in the Black Sea, and found the Romanian coast and parts north to the coastal area of the Ukraine (up to Odessa) to be suitable for combined wind-wave exploitation. Iglesias and Carballo(2010a, 2010b, 2011a, 2011b) and Khojasteh et al. (2018) provided an in-depth and thorough overview of the wave energy status in Spain and Asia, which filled a knowledge gap in this region. Researchers have made significant analyses of the climatic characteristics of wave energy, which provide reference for the site selection and long-term planning of wave energy projects, such as wave power generation and seawater desalination. However, research on the short-term forecasting of wave energy is relatively scant (Widén et al., 2015), and is urgently required for the effective daily operation of wave energy projects. As with wind and solar energy, 1–72-hour energy forecasting can help ensure the continuity of the business operation of power systems (e.g., unit scheduling, power trading), and 3–7-day energy forecasts can provide data for the maintenance planning of power farms and electrical grids (Foley et al., 2012; Mérigaud et al., 2017).
Bedard (2009) used the WW3 numerical wave model to forecast short-term wave energy, and obtained a good result with a precision of 0.30 – 0.35 m for the significant wave height (SWH) and 1.4 – 1.5 s for the wave period. Pinson et al. (2012) used a log-normal assumption to forecast wave power for 13 locations in North America and obtained good results. Hadadpour et al. (2013) used an artificial neural network to forecast wave energy, and obtained good agreement between the forecasted and observed values. Berastegi et al. (2015b) produced a wave-power forecast at three coastal buoys in Spain, which made a significant contribution to the efficient development of grid management strategies. Reikard (2009) conducted two experiments in wave energy forecasting for three sites in the Pacific Northwest, and the results revealed that timeseries models forecast more accurately over short horizons, but the degree of error increases rapidly with extensions of the horizon. Reikard et al. (2015a) also presented wave energy forecasts for a series of locations in western Canada, the Atlantic and Pacific Oceans, and the Gulf of Mexico and achieved good results. All the above works have made positive contributions based on the inherent predictability of wave energy.
Significant contributions to the short-term forecasting of wave energy have been made in a number of studies (Jeon and Taylor, 2016; Gordon et al., 2017). Overall, the traditional wave energy forecast scheme has mainly focused on wave power, SWH, and wave period, and a range of other key factors have been typically neglected. These factors include the effective wave height occurrence (EWHO), co-occurrence of wave power-direction, co-occurrence of SWH-wave period, and energy storage, which are closely related to effective energy output, capture efficiency, and conversion efficiency. This study proposes a wave-energy short-term forecast scheme that fully considers the above key indicators.
2 Data and Methods 2.1 MethodologyAs a case study for our proposed wave-energy shortterm forecast scheme, we used the NIO and obtained rich forecast factors. Although the traditional forecast scheme for wave energy mainly focuses on the SWH, wave period, and wave power, in the actual utilization of wave energy, the EWHO reflects the availability of energy. A series of key factors closely related to the capture efficiency and conversion efficiency are analyzed in the study of the climatic characteristics of wave energy, but these are omitted in short-term forecasts. For example, the co-occurrence of wave power-wave direction is closely related to the capture efficiency, the co-occurrence of SWH-wave period is a good reflection of the sea conditions, and the short-term energy storage reflects the energy output over the next several days. Therefore, in wave energy forecasts, these key indicators must be fully considered. Numerical simulation is an effective way to forecast wave energy. In the simulation of regional waves, the regional nesting method is usually adopted, with better simulation results achieved when using an extended area, which provides boundary conditions for the focus area. However, the proper selection of the extended area is difficult. The underlying principle is to minimize the extended area as much as possible to improve the calculation efficiency of the wave model and ensure simulation accuracy at the same time. In this study, we developed a rational method for selecting the extended area for wave-energy numerical forecasting in the SCS and North Indian Ocean (NIO), whereby different boundary conditions are compared using the WW3 numerical wave model (Ardhuin et al., 2003, 2009; Ardhuin and Magne, 2007; Resio and Perrie, 2008; Tolman, 2009, 2011, 2013). As the northern, eastern, and western boundaries of the focus area (SCS and NIO, 30˚– 130˚E, 15˚–30˚N) are mainly land, this study primarily compares and analyzes the effects of different southern boundaries on the numerical simulation of wave energy. Three simulation schemes are designed: no expansion of the southern boundary (scheme-1), expansion of the southern boundary to the tropical waters of the SIO (scheme-2), and expansion of the southern boundary to encompass the SIO westerly (scheme-3), as shown in Fig. 1.
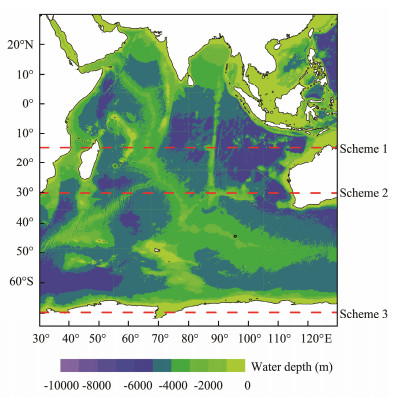
|
Fig. 1 South boundary of the three simulation schemes. |
Two periods were selected for study: On December 7– 12, 2016, tropical cyclone 'VARDAH' occurred in the Bay of Bengal, and in mid-September 2013, a strong swell process occurred in the SIO westerly, which may have affected the NIO. The precision of the simulated data is verified by comparing it with satellite and buoy data. Then, the accuracy of the three schemes are compared and analyzed. Lastly, the simulated wave data with greatest precision among the three schemes are selected to forecast the wave energy.
2.2 DataWind data: The ERA-Interim wind data held at the European Centre for Medium-Range Weather Forecasts (ECMWF) is used to drive the WW3 model. The production of ERA-Interim follows the ERA-40 reanalysis (Caires and Sterl, 2005; Semedo et al., 2011), and represents a significant improvement in the assimilation method used and the application of observation data. The temporal resolution of the data is 6-hourly, and the spatial resolution used in this study is 0.125˚×0.125˚. The time period ranges from January 1979 to the present. The spatial range is 90˚S–90˚N and 180˚W–180˚E. Comparisons of the ERA-Interim wind dataset with observation data has shown it to have high precision (Song et al., 2005; Bao and Zhang, 2013; Ma and Bian, 2014; Zheng and Li, 2017b; Alves, 2006; Bhowmick et al., 2011). This dataset is available at http://data-portal.ecmwf.int/data/d/interim_daily/.
Observed wave data: Wave data obtained from both satellite and buoys are used to verify the precision of the proposed wave simulation schemes. The SWH obtained from Jason-2 (SWH-Jason-2) is used to verify the precision of the simulated wave data obtained during cyclone 'VARDAH'. With the development of marine remotesensing technology, the SWHs obtained by the inversion of satellite data have been close to those obtained by buoy observations (Qi et al., 2003; Liu, 2005; Zhou et al., 2007; Zheng and Li, 2011; Zhou and Yang, 2008). The Jason-2 satellite data is available at http://topex-www.jpl.nasa.gov/mission/jason-1.html. Buoy data is used to verify the precision of the simulated wave data during the strong swell process that occurred in the SIO westerly in mid-September 2013. The buoy data used in this study was obtained in Sri Lanka (Luo and Zhu, 2018), where wave and water levels were measured for one year from April 2013 to April 2014 by a self-contained wave buoy at a depth of 10 m and at water level.
3 Comparison of Precision of the Three Schemes 3.1 Validation of Simulations During a Tropical CycloneThe SWHs simulated by the three schemes during tropical cyclone 'VARDAH' are individually interpolated with the satellite orbit. The simulation accuracies of the three schemes are then compared. To determine regional differences in the simulation precision, the accuracies of the simulated wave data in the Arabian Sea, the Bay of Bengal, and the SCS are calculated separately. Fig. 2 shows a quantile-quantile (QQ) plot of the simulated and observed SWHs.
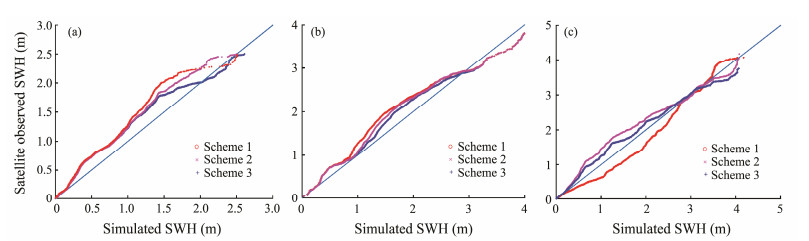
|
Fig. 2 Quantile-quantile plots comparing simulated SWH and observed SWH derived from Jason-2 for scheme-1, scheme-2, and scheme-3 in the Arabian Sea (a), Bay of Bengal (b), and South China Sea (c). |
From the QQ plot, we can see that the three schemes are generally effective in simulating wave behavior in the Arabian Sea, the Bay of Bengal, and the SCS. As the SCS is a relatively closed sea area, variations in its southern boundary have no significant impact on the simulation results. As such, the three simulation schemes have similar accuracy in the SCS. However, different southern boundaries have a significant impact on the wave simulation of the NIO, with the simulation accuracy of scheme-2 being better than that of scheme-1, and scheme-3 being the best. A previous study showed that the swell triggered by the SIO westerly has a significant impact on the NIO (Bhowmick et al., 2011). The southern boundary of scheme-2 is more southward than that of scheme-1, which makes it conducive to taking into account the swell of the SIO. Scheme-3 covers the entire Indian Ocean, including the SIO westerly. As such, scheme-3 can more thoroughly consider the swell of the SIO than scheme-2, which means the accuracy of the simulation wave data it obtains is higher.
To quantitatively determine the accuracy of the simulated wave data, we also calculate the correlation coefficient (CC), root mean square error (RMSE), bias, mean absolute error (MAE), and normalized root mean square error (NRMSE), as shown in Table 1. The simulated SWH values obtained by the three schemes show an overall high correlation with the SWH-Jason-2 in the Arabian Sea, the Bay of Bengal, and the SCS, with a CC greater than 0.8. The bias and MAE are less than 0.3 m, the NRMSE and RMSE are less than 0.4 m, and the scatter index is less than 0.3. Overall, the WW3 model is better able to simulate the waves in the SCS than in the NIO. In the SCS, the errors in the wave data obtained by the three schemes are similar. In the Arabian Sea and the Bay of Bengal, the degree of error obtained by scheme-2 is smaller than that of scheme-1, and that of scheme-3 is the smallest. Bedard (2009) used WW3 for the short-term forecasting of a wave power plant in northern California. Compared with those simulation results, the mean absolute accuracy of the simulated SWH in this study (0.30– 0.35 m) shows an improvement.
|
|
Table 1 Precision of the wave simulation schemes during tropical cyclone 'VARDAH' |
In addition, we also quantitatively calculate the degree of improvement in accuracy for scheme-2 and scheme-3, as compared with scheme-1. Taking the CC of scheme-2 (CC2) in the Arabian Sea as an example, (CC2-CC1)/CC1 represents an improvement of CC2, as shown in Table 2. Compared with those of scheme-1 and scheme-2, the improvement in the precision of scheme-3 is obvious in the NIO, especially in the Bay of Bengal (with an increase in CC and decreases in bias, MAE, RMSE, and NRMSE).
|
|
Table 2 Improvement in accuracy of scheme-2 and scheme-3, as compared with scheme-1, during tropical cyclone 'VARDAH' (unit: %) |
The simulated SWH during a strong swell process (mid-September 2013) obtained by the three schemes is verified by comparison with the buoy data, as shown in Fig. 3. As a whole, the simulated SWH obtained from scheme-3 agrees well with the observed SWH. The precisions of scheme-1 and scheme-2 are much lower than that of scheme-3. For September 12, 2013, in particular, a strong wave process is observable in both buoy data and the SWH obtained from scheme-3, whereas this strong wave process is not well exhibited by scheme-1 or scheme-2.
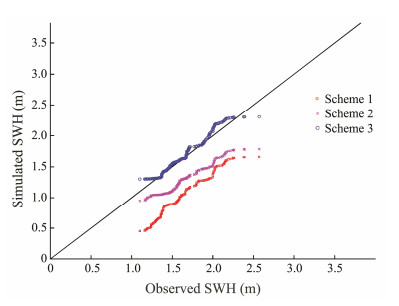
|
Fig. 3 Comparison of quantile-quantile plots for buoy observation SWH and simulated SWH obtained by scheme-1, scheme-2, and scheme-3 during a strong swell process in mid-September 2013. |
To quantitatively determine the precision of the simulated wave data, we calculated the CC, RMSE, bias, MAE, and NRMSE values of the buoy and simulation data, which are presented in Table 3. The CC values of scheme-2 and scheme-3 are 0.725 and 0.869, respectively, which are obviously higher than that of scheme-1 (0.630). Regarding the bias, the simulated SWHs obtained by scheme-1 and scheme-2 are smaller than that of the buoy data. The bias of scheme-3 is the smallest, which means that a similar average value was obtained by the buoy data and the wave data from scheme-3. The MAE, RMSE, and NRMSE values of scheme-2 are much smaller than those of scheme-1. The MAE, RMSE, and NRMSE values of scheme-3 are the smallest. Table 4 lists the obviously better precision of scheme-2 and scheme-3 as compared with that of scheme-1.
|
|
Table 3 Precision of wave data obtained by the three schemes for a strong swell process in mid-September 2013 |
|
|
Table 4 Accuracy improvements of scheme-2 and scheme-3 as compared with scheme-1 for a strong swell process in mid-September 2013 (unit: %) |
Based on the above analysis, it is evident that the accuracy of scheme-3 is the best. Therefore, the subsequent analysis is based on the simulated wave data of scheme-3. As the boundary condition for the SCS in this study does not cover the effect of swells propagating from the Pacific, we mainly examine the short-term forecasts of wave energy for the NIO. The forecast parameters include a comprehensive range of key factors that are closely related to the effective energy output, capture efficiency, and conversion efficiency: wave power, SWH, wave period, EWHO, weekly total storage, weekly effective storage, co-occurrence of wave power-wave direction, and co-occurrence of SWH-wave period.
4.1 Method for Calculating Wave PowerThe wave power calculation method is as follows (Cornett, 2008; Iglesias and Carballo, 2009; Vosough, 2011; Wan et al., 2015, 2016):
In shallow water (d/λ < 1/20),
| ${P_w} = \frac{{\rho g}}{{16}}H_s^2\sqrt {gd} ;$ | (1) |
In deep water (d/λ ≥ 1/2),
| ${P_w} = \frac{{\rho {g^2}}}{{64{\rm{ \mathsf{ π} }}}}H_s^2{T_e} = 0.49H_s^2{T_e};$ | (2) |
In water of medium depth (1/20 ≤ d/λ < 1/2),
| ${P_w} = \bar E(\frac{{g{T_e}}}{{2{\rm{ \mathsf{ π} }}}}\tanh kd)[\frac{1}{2}(1 + \frac{{2kd}}{{\sinh 2kd}})].$ | (3) |
Pw is the wave power (kW m−1), Hs is the SWH (m), Te is the energy period (s), d is the water depth (m), k = 2π/λ, and λ is the wave length (m).
4.2 Regional Forecasting of Wave Energy 4.2.1 Significant wave height and wave periodBased on the hindcast wave data from scheme-3, Fig. 4 presents the SWH and wave period during tropical cyclone 'VARDAH'. During this period, the SWH and wave period in the Bay of Bengal are larger than those in the Arabian Sea overall. In the Bay of Bengal, the cyclonic characteristics are well reflected by the SWH.
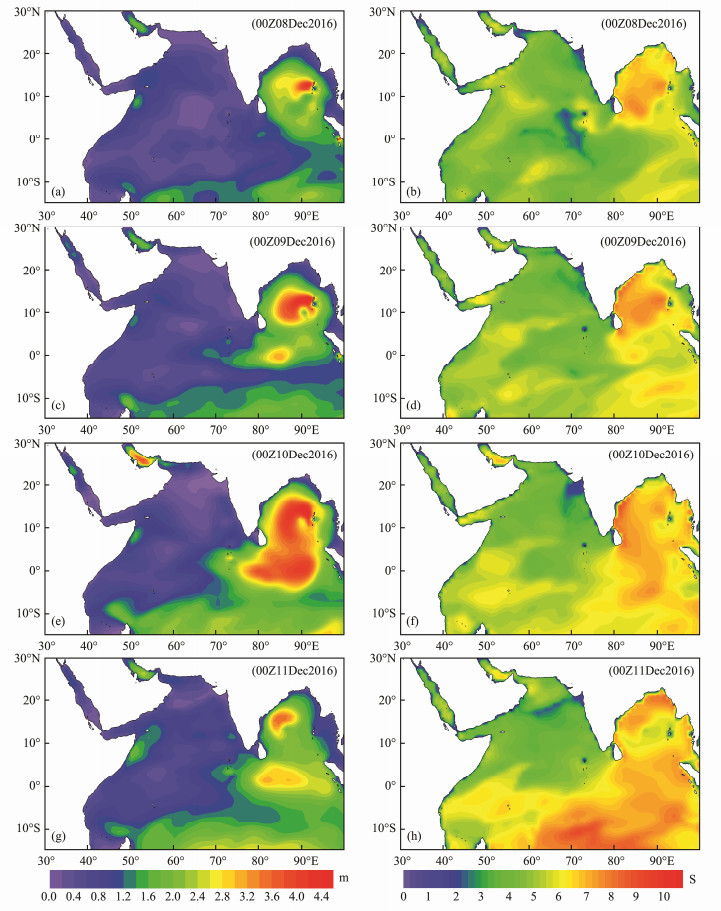
|
Fig. 4 Significant wave height (left) and wave period (right) during tropical cyclone 'VARDAH'. |
For December 8 to 12 in the Arabian Sea, the SWH and wave period are less than 1.0 m and less than 5 s, respectively, due to the absence of any typical weather phenomenon. For December 8, the SWH in most of the Bay of Bengal is higher than 1.6 m, and in the large center it is higher than 4.0 m (a small circular area to the west of the Andaman Islands). The wave period is 6 – 8 s, with a spatial distribution of larger wave periods in the northwest and smaller wave periods in the southeast. For December 9, with increased cyclone intensity, the range of the SWH area expands significantly to greater than 4.0 m. The wave period remains 6 – 8 s in most of the Bay of Bengal, with a relatively small region located to the northeast of the Andaman Islands. For December 10, the range of the SWH area greater than 4.0 m reaches its peak value. More than half of the Bay of Bengal and a large region in southeast Sri Lanka have an SWH higher than 4.4 m. The large wave period region moves offshore of the eastern Indian Peninsula and eastern Sri Lanka. For December 11 to 12, as the tropical cyclone makes landfall, the SWH decreases rapidly to less than 2.0 m in most regions, with the wave period offshore smaller than that nearshore.
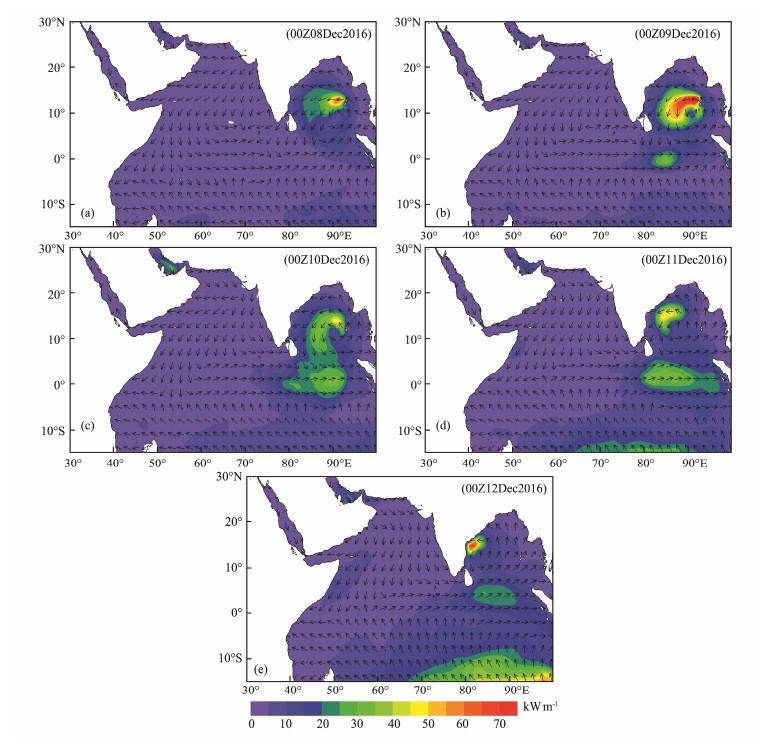
4.2.2 Wave powerBased on the hindcast data, we obtained the hourly wave power for the tropical cyclone 'VARDAH' period, as shown in Fig. 5. For easy observation, the background color indicates the wave power, and the unit vector arrow the wave direction (same as below).
|
Fig. 5 Wave power and wave direction in the North Indian Ocean during tropical cyclone 'VARDAH'. |
At 00:00 on December 8 in the Bay of Bengal, 'VARDAH' is in the development stage, with the wave power in most of the Bay of Bengal greater than 10 kW m−1, and in the large center it is greater than 40 kW m−1. The wave power in the Arabian Sea and tropical Indian Ocean is less than 5 kW m−1. At 00:00 on December 9, with the development of 'VARDAH', the wave power in a large range of the middle of the Bay of Bengal is greater than 30 kW m−1, and ranges up to 70 kW m−1 in the large center. The wave power in the Arabian Sea and tropical Indian Ocean is less than 5 kW m−1. At 00:00 on December 10, the wave power range is 10 – 30 kW m−1 in most of the Bay of Bengal and less than 5 kW m−1 in the Arabian Sea. We note that the wave power increases in the tropical SIO, with some areas reaching 5–10 kW m−1. At 00:00 on December 11, the wave power in the Arabian Sea is less than 5 kW m−1, and that in the tropical SIO continues to strengthen. At 00:00 on December 12, with 'VARDAH' landing on the Indian Peninsula, the wave power in the Bay of Bengal decreases significantly, with the majority of the region at 5–10 kW m−1. The wave power in the Arabian Sea is less than 5 kW m−1. We note that the wave power in the tropical SIO continues to increase to approximately 30 kW m−1 at around 15˚S, but decreases with increasing latitude, with the isoline curving to the north. It is clear that this is due to the swell propagating from the SIO to the NIO.
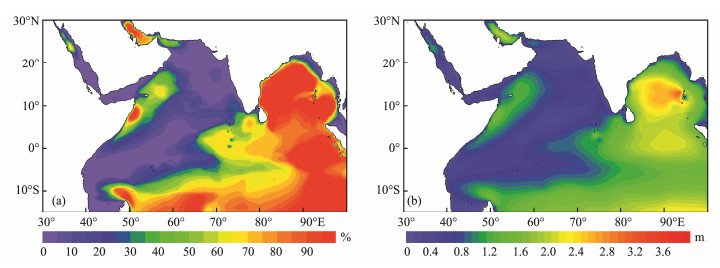
4.2.3 Available rateUsually, when the SWH is higher than 1.3 m, its can be used to understand the development of wave energy (Shen and Qian, 2003), and once the SWH reaches or exceeds 4.0 m, it has greater destruction capability (Zheng et al., 2013, 2014a). Zheng and Li (2018) referred to the SWH values between 1.3 – 4.0 m as effective wave heights for wave energy development. Of course, as the absorbing capacity of wave energy devices continues to increase, the range of effective wave heights will expand accordingly. The EWHO reflects the availability of wave energy, which is one of the most important factors for wave energy development. Based on the hourly SWH, the EWHO for future one-week forecasting (00:00z07Dec–23:00z13Dec 2016, same as below) of the NIO can be determined. That is, the EWHO is forecasted for the next seven days, as shown in Fig. 6a. The future SWH for one week is also calculated, as shown in Fig. 6b. The EWHO in the Bay of Bengal is optimistic, at above 90%. However, that for the Arabian Sea is generally low, with most of the EWHO values less than 20%. Due to the impact of the northward swells from the SIO, the EWHO in the tropical SIO is optimistic, with most regions more than 50% and large value centers more than 90%. The SWH and EWHO have an overall agreement.
|
Fig. 6 Available rate of wave energy (a) and average significant wave height (b) for the following week. |
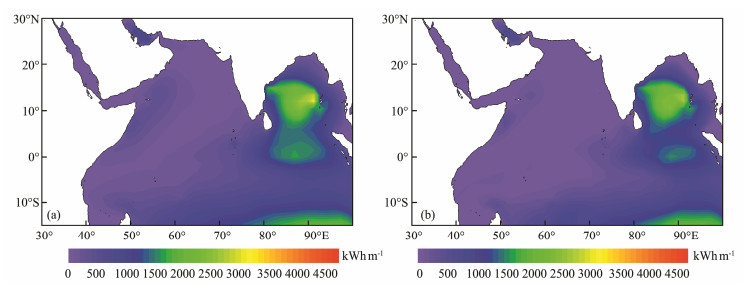
Wave energy storage is closely related to the output of resources (Zheng et al., 2014b). Based on the effective storage of wave energy combined with the conversion efficiency of the equipment, engineers can estimate the wave energy output. Researchers have devoted much effort to determining the annual wave energy storage in the global oceans. However, there has been scant work on the short-term forecasting of wave-energy storage, which is needed as a basis for unit commitment and dispatch and electricity trading. Based on the hourly simulated wave data obtained by scheme-3, future forecasts are made of the total storage and effective storage of wave energy for one week, as shown in Fig. 7. The method used to calculate wave energy storage is as follows:
| ${E_{PT}} = \bar P * H, $ | (4) |
| ${E_{PE}} = \bar P * {H_E}, $ | (5) |
|
Fig. 7 Total storage and effective storage of wave energy for the next week. |
where EPT is the total storage of wave energy,
Total storage: The total wave-energy storage in the Bay of Bengal is greater than that in the Arabian Sea. Specifically, the total storage in the Bay of Bengal ranges between 1000 kWhm−1 and 2500 kWhm−1 and that in the Arabian Sea is less than 500 kWhm−1. Effective storage: The spatial distribution characteristic of the effective wave-energy storage has good overall consistency with that of total storage. The effective storage is close in value to the total storage in the Bay of Bengal and the tropical SIO for a high EWHO. The effective storage in the Arabian Sea is less than 300 kWhm−1.
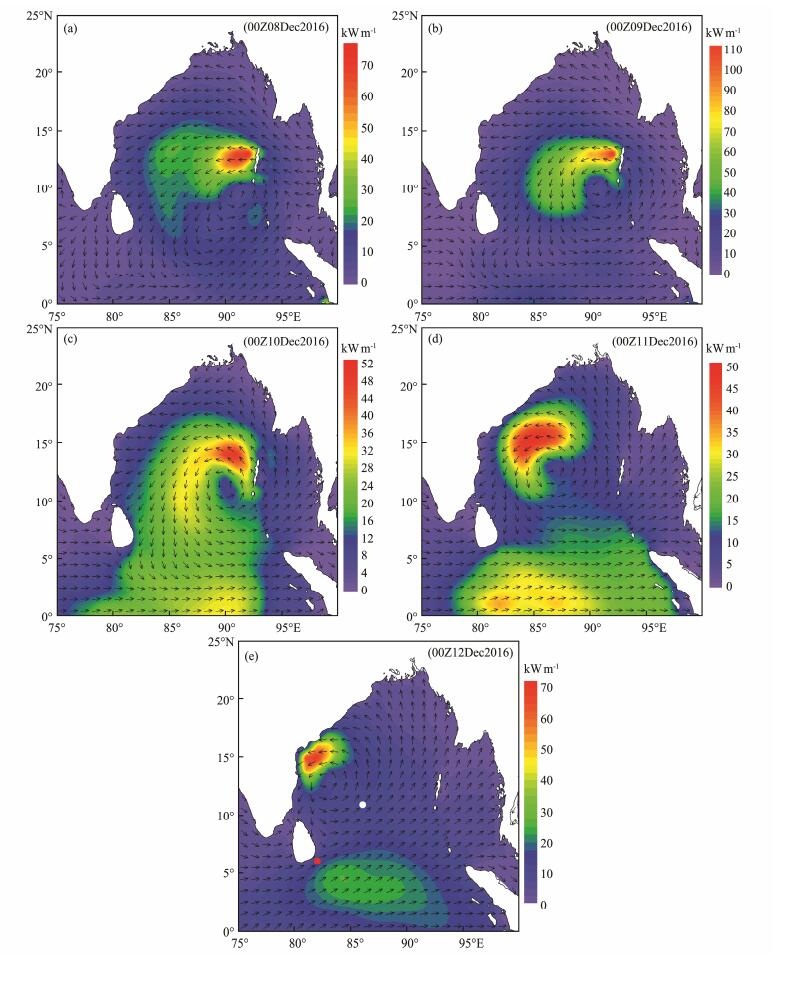
4.3 Wave Energy Forecasting for the Key Region and Key Points 4.3.1 Hourly wave power for the key regionIn the actual development of wave energy, more attention must be paid to the energy forecasting of the key region. Here, the Bay of Bengal is assumed to be the area of interest. Based on the hindcast data, the wave power and wave direction in the Bay of Bengal is contoured as shown in Fig. 8.
|
Fig. 8 Wave power and wave direction in the Bay of Bengal during cyclone 'VARDAH'. |
At 00:00 on December 8, neither the wave power nor wave direction showed a significant cyclonic structure. The large wave power values are distributed in the right half circle (right side of forward direction) of cyclone 'VARDAH', and reach 70 kW m−1 in the large center. At 00:00 on December 9, the cyclonic structures of wave power and wave direction are significant. A large wave power area is located in the front and right of the forward direction of cyclone 'VARDAH', with up to 110 kW m−1 in the large center. On December 10 – 11, with the cyclone moving westward, its intensity gradually weakens. On December 12, the cyclone makes landfall on the Indian peninsula and its influence on the Bay of Bengal gradually wanes.
4.3.2 Wave energy increases at key pointsThe direction of wave energy is closely related to the resource collection and conversion efficiency, and chaotic resources can seriously affect the efficiency of wave energy development and even the life of the device. Therefore, it is necessary to forecast the wave-energy direction. For this study, two wave power plants are assumed to be in the Bay of Bengal (the solid red dot in the last figure of Fig. 8 is site A and the solid white dot is site B). Increases in the wave energy (co-occurrence of wave power and wave direction) of sites A and B are forecasted, as shown in Fig. 9.
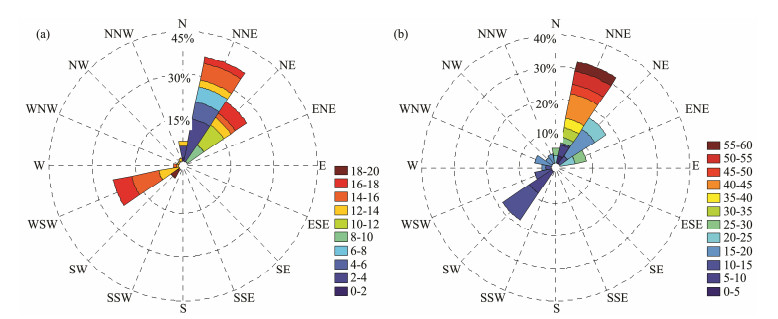
|
Fig. 9 Wave energy increases (co-occurrence of wave power-wave direction) at sites A (a) and B (b) for the time period during cyclone 'VARDAH'. |
For site A, the direction with the highest occurrence is north-northeast (NNE), followed by northeast (NE) and west-southwest (WSW). Strong wave power higher than 14 kW m−1 mainly comes from the WSW, followed by the NNE and NE, which is most likely due to the combined effect of cyclone 'VARDAH' and the swell propagation from the SIO. For site B, the direction with the highest occurrence is NNE, followed by NE and WSW. Strong wave power higher than 40 kW m−1 mainly comes from the NNE, most likely due to the effect of cyclone 'VARDAH'. A comparison of the wave energy increases at sites A and B reveals that site B is more significantly affected by cyclone 'VARDAH' and site A is more significantly affected by the swell propagation from the SIO.
4.3.3 Hourly wave power and direction in key pointsNext, we forecast the hourly wave power and wave direction for sites A and B in the next few days, as shown in Fig. 10. For site A, the wave power in the next week is greater than 2 kW m−1, and slowly increases. The wave direction is NE for December 7–10. After December 11, the wave direction changes to roughly west (W). For site B, due to the influence of cyclone 'VARDAH', for the next week, the wave power shows a single peak variation greater than 10 kW m−1, and reaches 60 kW m−1 at its peak. The wave direction is roughly north (N) for December 7–10. From 12:00 on December 11, the wave direction changes to southwest (SW).
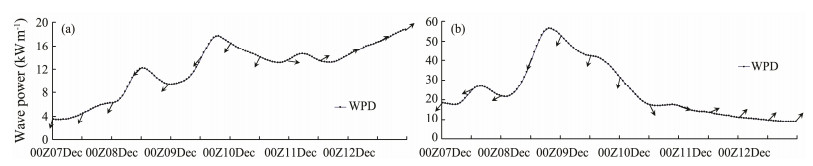
|
Fig. 10 Wave power and wave direction (unit black arrow) of site A (a) and site B (b) for the next week. |
Wave power greater than 2 kW m−1 is generally considered to be available, and greater than 20 kW m−1 as abundant (Zheng et al., 2012). Obviously, the wave energy values of sites A and B are in the available range for the next several days. The wave energy of site A is close to abundant after December 10, and that of site B is fairly abundant prior to 12:00 on December 10. In addition, the wave directions of sites A and B are relatively stable and less variable, with the wave energy mainly coming from the NE and SW, which is beneficial for the collection and conversion of wave energy.
4.3.4 Sea state contribution to wave energyBased on the hindcast data, the co-occurrences of SWH and wave period for sites A and B are obtained to determine the contribution of the sea state to the wave energy, as shown in Fig. 11. The sea state range of site A is mainly 1 – 3 m and 6 – 9 s, with an emphasis on 2 m and 7 s (up to 33%). The sea state range of site B is mainly 1 – 4 m and 5 – 8 s, with an emphasis on 2 m and 6 s (up to 33%). Site B is close to the middle of the Bay of Bengal and site A is located to the southeast of Sri Lanka. Therefore, site B is more affected by cyclone 'VARDAH' than site A, which means a higher occurrence of SWHs higher than 3 m at site B. Zheng et al. (2018) reported that swells generated by the SIO westerly can often propagate along the northeast to the Sri Lankan waters. This means that a swell in the SIO has a greater impact on site A than on site B, resulting in site A predominantly experiencing a wave period of 7 s, and site B by a wave period of 6 s.
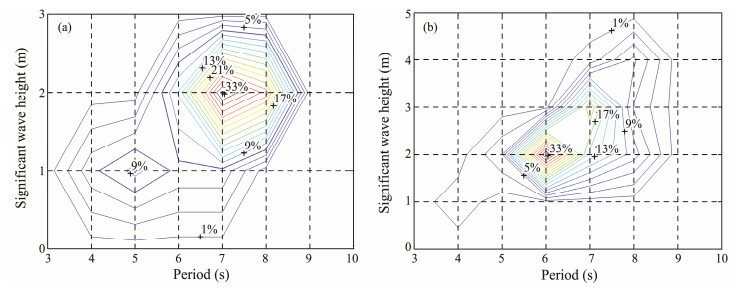
|
Fig. 11 Co-occurrence of SWH-period of site A (a) and site B (b) for the next week. |
By the above analysis, we find that the precision of simulated wave data in the NIO can be increased with the appropriate consideration of the swells originating from the SIO (scheme-2). With full consideration of the swells originating from the SIO to the NIO (scheme-3), the accuracy of the simulated wave data in the NIO is significantly improved. Therefore, in the numerical simulation of waves and wave energy in the NIO, it is necessary to fully consider the impact of the northward propagation of swells generated from the SIO westerly. Using the Indian Ocean as an expansion area to provide wave boundary conditions for the numerical simulation of waves in the NIO, we can take into full account the effects of swells originating from the SIO, thereby significantly enhancing the ability of wave models to simulate wave fields in the NIO.
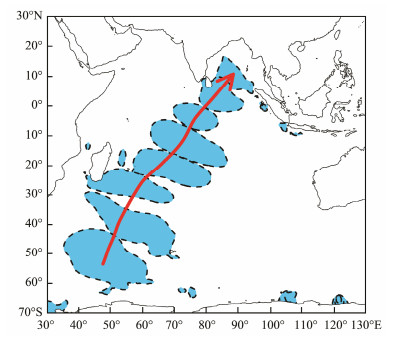
Alves (2006) reported that swells from the SIO have a significant impact on the NIO, as shown in Fig. 12. In addition, Zheng and Li (2017a) accurately mapped the propagation route of swells from the SIO westerly based on a comprehensive use of 6-hour zonal averages, the EOFs, and the simultaneous, lead, and lag correlation coefficients, as shown in Fig. 13. Both wavelet and cross-wavelet analyses were also used to verify the propagation characteristics. Studies have shown that swells originating from the SIO westerly typically propagate across the equator to the NIO, spreading to two main terminal regions: the main part spreading to Sri Lankan waters, and another branch spreading to the Christmas Island waters. Swell energy in the SIO westerly, the tropical Indian Ocean, the Sri Lankan waters, and the Christmas Island waters have a common period of quasi-weekly oscillation. The swell energy normally requires six days to propagate from the SIO westerly to the Sri Lankan and Christmas Island waters. When simulating the regional waves of the NIO, it is necessary to fully consider the impact of the swell originating from the SIO. Parvathy and Bhaskaran (2019), Sreelakshmi and Bhaskaran (2020), Murty et al. (2020), Remya et al. (2016), and Sabique et al. (2012) have made positive contributions to the research on swells in the Indian Ocean. In addition, they have reported that the swells generated from the SIO have a significant impact on the NIO.
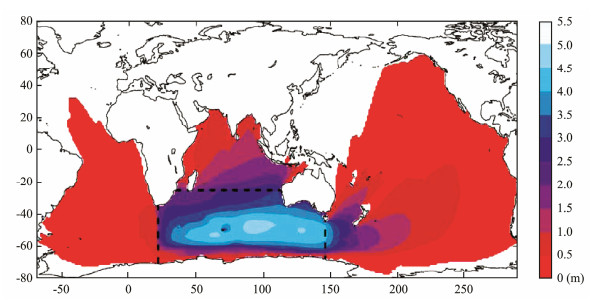
|
Fig. 12 Global fields of annual mean Hs (year 2000) originating from the extratropical South Indian Ocean (Alves, 2006). A cutoff level is imposed at locations with persistence ≤ 1 d. |
|
Fig. 13 Propagation route of swell energy of the southwest Indian Ocean in JJA 2001 (Zheng and Li, 2017a). |
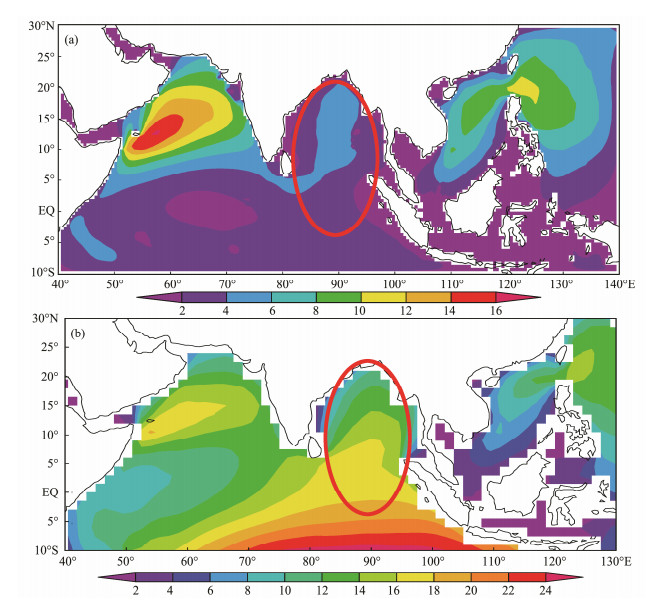
Based on the numerical experiments of this study, the swells originating from the SIO westerly are found to significantly impact the accuracy of the short-term forecasts of waves in the NIO. Here, we further explore the significance of the impact of swells from the SIO on the climatic characteristics of the wave energy in the NIO. Zhou et al. (2011) and Mei et al. (2010) obtained 44-year (1958 – 2001) hindcast wave data using ERA-40 wind data 10 m above the sea surface to drive the WW3 model. The simulation range is 10˚S–30˚N, 40˚–140˚E, which excludes swells from the SIO (similar to scheme-2 of this study). Based on the 44-year WW3 hindcast wave data obtained by Zhou et al. (2011) and Mei et al. (2010), we calculated the multi-year average wave power for the past 44 years, which is shown in Fig. 14a. Using the ERA-40 wave reanalysis from ECMWF, we also calculated the multi-year average wave power for the past 44 years, as shown in Fig. 14b. The ERA-40 wave reanalysis represents the first coupling of the wave and atmospheric circulation model simulation results, which has high precision and is widely used (Sterl and Caires, 2005; Uppala et al., 2006; Hemer et al., 2007). Here, the ERA-40 wave reanalysis is regarded as an actual wave field to validate the obtained wave power, based on the hindcast wave data obtained by Zhou et al. (2011) and Mei et al. (2010).
|
Fig. 14 Annual mean wave power based on the data from Mei et al. (2010) (a) and from ERA-40 wave reanalysis (b), unit: kW m−1. |
The spatial distribution of the wave power in the Arabian Sea and the SCS, as shown in Figs. 14a and 14b, maintain overall agreement. However, a great difference is found in the Bay of Bengal, where the wave power in most areas is 4 – 6 kW m−1, in the absence of full consideration of the swells from the SIO (Fig. 14a). The wave power value in the Bay of Bengal in Fig. 14b is obviously larger than that in Fig. 14a. In Fig. 14b, the wave power gradually decreases from south to north with an arc-shape northward projection, which illustrates the obvious propagation of swells from the SIO to the NIO. Therefore, in the NIO, both short-term numerical forecasts and climatic characteristic analyses of the wave energy must fully consider the impact of swells originating from the SIO westerly. In regional wave simulations in the NIO and the rest of the world, the impact of swells far away from the focus area should also be considered. Using the method described by Zheng et al. (2018), we can trace the source of swells in the focus area to further clarify the scope of the extended area. The simulation results of the extended area can then be used to provide boundary conditions for the focus area, and thereby improve the precision of the simulated wave data of the focus area.
Ocean waves play an important role in global climate change, air-sea interaction, disaster prevention and reduction, and wave-energy development. In the ocean, some sea areas are significantly affected by the swells generated from other regions. Simulations of ocean waves without full consideration of the swells generated from other regions may result in misleading conclusions regarding the climatic characteristics of wave energy. This could also result in a misunderstanding of global climate change, air-sea interaction, and other factors, which will then require reanalysis in future work.
6 Conclusions and ProspectsThe objective of this study was to propose a short-term forecast program for wave energy, using the NIO as a case study. The results show that it is feasible to generate short-term forecasts of wave energy using the WW3 numerical wave model. Compared with the traditional parameters of short-term forecast schemes for wave energy, which mainly focus on wave power, SWH, and wave period, this short-term forecast scheme is more comprehensive, including the wave power, SWH, wave period, weekly effective wave height occurrence (EWHO), weekly total storage, weekly effective storage, co-occurrence of wave power-wave direction, and sea condition contributions to wave energy (co-occurrence of the SWH-wave period). The inclusion of this many factors enables the WW3 numerical model to better meet the actual demands associated with daily wave-energy utilization. During cyclone 'VARDAH', the large value center of wave power reaches 70 kW m−1. In this period, the available wave energy in most of the Bay of Bengal is higher than 80%. In the Arabian Sea, the north and northeast region is a low wave energy center (less than 20%), and the southwest region is a relatively large center. The range of the total wave energy storage for the focus period is 1000–2500 kWhm−1 in the Bay of Bengal and less than 500 kWhm−1 in the Arabian Sea.
We conducted an experiment on the southern-boundary variability and its impact on the simulation precision of wave energy in the NIO. Three south boundary conditions were considered: no expansion of the southern boundary (scheme-1), southern boundary extension to the tropical SIO (scheme-2), and southern boundary extension to the SIO westerly (scheme-3). During tropical cyclone 'VARDAH', compared with scheme-1, the error of scheme-2 is reduced by 10%–18% in the Arabian Sea and 23%–32% in the Bay of Bengal. Compared with scheme-1, the error of scheme-3 is reduced by 15%–25% in the Arabian Sea and 26%–38% in the Bay of Bengal. During the strong swell process from the SIO westerly in mid-September 2013, compared with scheme-1 and scheme-2, the improvement obtained by scheme-3 is much more significant, especially in the Bay of Bengal. A rational selection method is thus obtained for extending the area of wave energy numerical forecasting for the NIO: in the regional nesting of numerical wave simulations for the NIO, the southern boundary must cover the SIO westerly.
A short-term forecast scheme for wave energy was proposed based on the use of ERA-Interim wind data to drive the WW3 wave model. In the actual short-term forecast of wave energy, wind production can be replaced by shortterm forecast wind data (such as Global Forecast System wind productions) for use in the daily operation of wave-energy development. In addition, short-term forecast parameters can be added according to the actual demand, such as the occurrence of different energy levels (e.g., wave power greater than 2 kW m−1, greater than 10 kW m−1, greater than 20 kW m−1, etc.), to better meet actual demand. This study explored the southern-boundary conditions that enable the most accurate short-term forecasts of wave energy for the NIO. Based on the results, in our next work, we will compare the accuracy and efficiency of numerical calculations under different spatial-resolution scenarios to achieve a balance between accuracy and efficiency in calculations of wave-energy short-term forecasts.
AcknowledgementsThis work was supported by the open fund project of Shandong Provincial Key Laboratory of Ocean Engineering, Ocean University of China (No. kloe201901), and the Major International (Regional) Joint Research Project of the National Science Foundation of China (No. 4152010 4008).
Akpinar, A. and Bingölbali, B., 2016. Long-term variations of wind and wave conditions in the coastal regions of the Black Sea. Natural Hazards, 84(1): 69-92. DOI:10.1007/s11069-016-2407-9 (  0) 0) |
Akpinar, A. and Kömürcü, M. I., 2013. Assessment of wave energy resource of the Black Sea based on 15-year numerical hindcast data. Applied Energy, 101: 502-512. DOI:10.1016/j.apenergy.2012.06.005 (  0) 0) |
Akpinar, A. and Poncede Leon, S., 2016. Assessment of the wind re-analysis in the modelling of an extreme sea state in the Black Sea. Dynamics of Atmospheres and Oceans, 73: 61-75. DOI:10.1016/j.dynatmoce.2015.12.002 (  0) 0) |
Akpinar, A., Bingölbali, B. and Vledder, G. P. V., 2017. longterm analysis of wave power potential in the Black Sea, based on 31-year SWAN simulations. Ocean Engineering, 130: 482-497. DOI:10.1016/j.oceaneng.2016.12.023 (  0) 0) |
Alves, J. H., 2006. Numerical modeling of ocean swell contributions to the global wind-wave climate. Ocean Modelling, 11: 98-122. DOI:10.1016/j.ocemod.2004.11.007 (  0) 0) |
Ardhuin, F. and Magne, R., 2007. Scattering of surface gravity waves by bottom topography with a current. Journal of Fluid Mechanics, 576: 235-264. DOI:10.1017/S0022112006004484 (  0) 0) |
Ardhuin, F., Chapron, B. and Collard, F., 2009. Ocean swell evolution from distant storms. Geohysical Research Letters, 36: L06607. DOI:10.1029/2008GL037030 (  0) 0) |
Ardhuin, F., O'Reilly, W. C., Herbers, T. H. C. and Jessen, P. F., 2003. Swell transformation across the continental shelf. Part Ⅰ: Attenuation and directional broadening. Journal of Physical Oceanography, 33: 1921-1939. (  0) 0) |
Bao, X. H. and Zhang, F. Q., 2013. Evaluation of NCEP-CFSR, NCEP-NCAR, ERA-Interim, and ERA-40 reanalysis datasets against independent sounding observations over the Tibetan Plateau. Journal of Climate, 26: 206-214. DOI:10.1175/JCLI-D-12-00056.1 (  0) 0) |
Bedard, R., 2009. Wave energy forecasting accuracy as a function of forecast time horizon. EPRI-WP-013, Available : http://oceanenergy.epri.com/attachments/wave/reports/013_Wave_Energy_Forecasting_Report.pdf.
(  0) 0) |
Berastegi, G. I., Sáenz, J., Esnaola, G., Agustin, E. and Ulazia, A., 2015a. Short-term forecasting of the wave energy flux Analogues, random forests, and physics-based models. Ocean Engineering, 104: 530-539. DOI:10.1016/j.oceaneng.2015.05.038 (  0) 0) |
Berastegi, G. I., Sáenz, J., Esnaola, G., Ezcurra, A., Alain, U., Naiara, R. and Gorka, G., 2015b. Wave energy flux vectorial prediction at three coastal buoys in Spain. Presented at the Sixth International Workshop on Marine Technology. Martech: 122-125. (  0) 0) |
Bhowmick, S. A., Kumar, R., Chaudhuri, S. and Sarkar, A., 2011. Swell propagation over Indian Ocean region. International Journal of Ocean and Climate Systems, 2(2): 87-99. DOI:10.1260/1759-3131.2.2.87 (  0) 0) |
Caires, S. and Sterl, A., 2005. 100-year return value estimates for ocean wind speed and significant wave height from the ERA-40 data. Journal of Climate, 18: 1032-1048. DOI:10.1175/JCLI-3312.1 (  0) 0) |
Cornett, A. M., 2008. A global wave energy resource assessment. The Eighteenth (2008) International Offshore and Polar Engineering Conference. Vancouver, Canada: 1-8. (  0) 0) |
Esteban, M. D., Espada, J. M., Ortega, J. M., López-Gutiérrez, J. S. and Negro, V., 2019. What about marine renewable energies in Spain?. Journal of Marine Science and Engineering, 7(8): 249. DOI:10.3390/jmse7080249 (  0) 0) |
Foley, A. M., Leahy, P. G., Marvuglia, A. and McKeogh, E. J., 2012. Current methods and advances in forecasting of wind power generation. Renewable Energy, 37(1): 1-8. DOI:10.1016/j.renene.2011.05.033 (  0) 0) |
Gordon, R., Bryson, R. and Bidlot, J. R., 2017. Wave energy worldwide: Simulating wave farms, forecasting, and calculating reserves. International Journal of Marine Energy, 17: 156-185. DOI:10.1016/j.ijome.2017.01.004 (  0) 0) |
Hadadpour, S., Etemad-Shahidi, A. and Kamranzad, B., 2013. Wave energy forecasting using artificial neural networks in the Caspian Sea. Maritime Engineering, 167: 42-52. (  0) 0) |
Hemer, M. A., Church, J. A. and Hunter, J. R., 2007. Waves and climate change on the Australian coast. Journal of Coastal Research, 50: 432-437. (  0) 0) |
Iglesias, G. and Carballo, R., 2009. Wave energy potential along the death coast (Spain). Energy, 34: 1963-1975. DOI:10.1016/j.energy.2009.08.004 (  0) 0) |
Iglesias, G. and Carballo, R., 2010a. Wave energy resource in the Estaca de Bares area (Spain). Renewable Energy, 35: 1574-1584. DOI:10.1016/j.renene.2009.10.019 (  0) 0) |
Iglesias, G. and Carballo, R., 2010b. Offshore and inshore wave energy assessment: Asturias (N Spain). Energy, 35(5): 1964-1972. DOI:10.1016/j.energy.2010.01.011 (  0) 0) |
Iglesias, G. and Carballo, R., 2011a. Choosing the site for the first wave farm in a region: A case study in the Galician southwest (Spain). Energy, 36(9): 5525-5531. DOI:10.1016/j.energy.2011.07.022 (  0) 0) |
Iglesias, G. and Carballo, R., 2011b. Wave power for La Isla Bonita. Energy, 35: 5013-5021. (  0) 0) |
Jeon, J. and Taylor, J. W., 2016. Short-term density forecasting of wave energy using ARMA-GARCH models and kernel density estimation. International Journal of Forecasting, 32(3): 991-1004. DOI:10.1016/j.ijforecast.2015.11.003 (  0) 0) |
Kamranzad, B., Chegini, V. and Etemad, -Shahidi A., 2016. Temporal-spatial variation of wave energy and nearshore hotspots in the Gulf of Oman based on locally generated wind waves. Renewable Energy, 94: 341-352. DOI:10.1016/j.renene.2016.03.084 (  0) 0) |
Kamranzad, B., Etemad-Shahidi, A., Chegini, V. and Yeganeh-Bakhtiary, A., 2015. Climate change impact on wave energy in the Persian Gulf. Ocean Dynamics, 65: 777-794. DOI:10.1007/s10236-015-0833-y (  0) 0) |
Khojasteh, D., Mousavi, S. M., Glamore, W. and Iglesias, G., 2018. Wave energy status in Asia. Ocean Engineering, 169: 344-358. DOI:10.1016/j.oceaneng.2018.09.034 (  0) 0) |
Liang, B. C., Fan, F., Yin, Z. G., Shi, H. D. and Lee, D. Y., 2013. Numerical modelling of the nearshore wave energy resources of Shandong Peninsula, China. Renewable Energy, 57: 330-338. DOI:10.1016/j.renene.2013.01.052 (  0) 0) |
Liu, Y. G., 2005. Ocean Remote Sensing. Higher Education Publication, Beijing, 1-10.
(  0) 0) |
Luo, Y. and Zhu, L. S., 2018. Investigation of trends in extreme significant wave heights in the South China Sea. Aquatic Ecosystem Health & Management, 3: 1-31. (  0) 0) |
Ma, Y. F. and Bian, L. G., 2014. A surface climatological validation Of ECMWF ERA-Interim reanalysis and NCEP FNL analysis over East Antarctica. Chinese Journal of Polar Research, 26(4): 469-480. (  0) 0) |
Mei, Y., Song, S. and Zhou, L., 2010. Annual variation characteristics of wave fields and wind fields over the North Indian Ocean and South China Sea. Marine Forecasts, 27(5): 27-33. (  0) 0) |
Mérigaud, A., Ramos, V., Paparella, F. and Ringwood, J. V., 2017. Ocean forecasting for wave energy production. Journal of Marine Research, 75: 459-505. DOI:10.1357/002224017821836752 (  0) 0) |
Murty, P. L. N., Srinivas, K. S., Rao, E. P. R., Bhaskaran, P. K., Shenoi, S. S. C. and Padmanabham, J., 2020. Improved cyclonic wind fields over the Bay of Bengal and their application in storm surge and wave computations. Applied Ocean Research, 95: 102048. DOI:10.1016/j.apor.2019.102048 (  0) 0) |
Parvathy, K. G. and Bhaskaran, P. K., 2019. Nearshore modelling of wind-waves and its attenuation characteristics over a mud dominated shelf in the Head Bay of Bengal. Regional Studies in Marine Science, 29: 100665. DOI:10.1016/j.rsma.2019.100665 (  0) 0) |
Pinson, P., Reikard, G. and Bidlotc, J. R., 2012. Probabilistic forecasting of the wave energy flux. Applied Energy, 93: 364-370. DOI:10.1016/j.apenergy.2011.12.040 (  0) 0) |
Qi, Y. Q., Zhu, B. C., Shi, P., Mao, Q. W. and Fan, C. W., 2003. Analysis of significant wave heights from WWATCH and TOPEX/Poseidon altimetry. Acta Oceanologica Sinica, 25(4): 1-9. (  0) 0) |
Reguero, B. G., Losada, I. J. and Méndez, F. J., 2015. A global wave power resource and its seasonal, interannual and longterm variability. Applied Energy, 148: 366-380. DOI:10.1016/j.apenergy.2015.03.114 (  0) 0) |
Reikard, G., 2009. Forecasting ocean wave energy: Tests of timeseries models. Ocean Engineering, 36: 348-356. DOI:10.1016/j.oceaneng.2009.01.003 (  0) 0) |
Reikard, G., Robertson, B. and Bidlot, J. R., 2015a. Combining wave energy with wind and solar: Short-term forecasting. Renewable Energy, 81: 442-456. DOI:10.1016/j.renene.2015.03.032 (  0) 0) |
Reikard, G., Robertson, B., Buckham, B., Jean-Raymond, B. and Clayton, H., 2015b. Simulating and forecasting ocean wave energy in western Canada. Ocean Engineering, 103: 223-236. DOI:10.1016/j.oceaneng.2015.04.081 (  0) 0) |
Remya, P. G., Vishnu, S., Kumar, B. P., Nair, T. M. B. and Rohith, B., 2016. Teleconnection between the North Indian Ocean high swell events and meteorological conditions over the southern Indian Ocean. Journal of Geophysical Research: Oceans, 121: 7476-7494. DOI:10.1002/2016JC011723 (  0) 0) |
Resio, D. T. and Perrie, W., 2008. A two-scale approximation for efficient representation of nonlinear energy transfers in a wind wave spectrum. Part Ⅰ: Theoretical development. Journal of Physical Oceanography, 38(12): 2801-2816. DOI:10.1175/2008JPO3713.1 (  0) 0) |
Rodriguez-Delgado, C., Bergillos, R. J. and Iglesias, G., 2019. Dual wave farms for energy production and coastal protection under sea level rise. Journal of Cleaner Production, 222: 364-372. DOI:10.1016/j.jclepro.2019.03.058 (  0) 0) |
Rusu, L., 2019. The wave and wind power potential in the western Black Sea. Renewable Energy, 139: 1146-1158. DOI:10.1016/j.renene.2019.03.017 (  0) 0) |
Rusu, L., Ganea, D. and Mereuta, E., 2018. A joint evaluation of wave and wind energy resources in the Black Sea. Energy Exploration & Exploitation, 38(2): 335-351. (  0) 0) |
Sabique, L., Annapurnaiah, K., Nair, T. M. B. and Srinivas, K., 2012. Contribution of southern Indian Ocean swells on the wave heights in the northern Indian Ocean – A modeling study. Ocean Engineering, 43: 113-120. DOI:10.1016/j.oceaneng.2011.12.024 (  0) 0) |
Semedo, A., Suselj, K., Rutgersson, A. and Sterl, A., 2011. A global view on the wind sea and swell climate and variability from ERA-40. Journal of Climate, 24: 1461-1479. DOI:10.1175/2010JCLI3718.1 (  0) 0) |
Shen, S. G. and Qian, X. Z., 2003. Resource Ocean: Exploitation and Utilization of the Rich Blue Treasury. Haichao Press, Beijing, 110-120.
(  0) 0) |
Song, L. N., Liu, Z. L. and Wang, F., 2015. Comparison of wind data from ERA-Interim and buoys in the Yellow and East China Seas. Chinese Journal of Oceanology and Limnology, 33(1): 282-288. DOI:10.1007/s00343-015-3326-4 (  0) 0) |
Sreelakshmi, S. and Bhaskaran, P. K., 2020. Regional wise characteristic study of significant wave height for the Indian Ocean. Climate Dynamics, 54(8): 3405-3423. DOI:10.1007/s00382-020-05186-6 (  0) 0) |
Sterl, A. and Caires, S., 2005. Climatology, variability and extrema of ocean waves – The web-based KNMI/ERA-40 wave atlas. International Journal of Climatology, 25(7): 963-997. DOI:10.1002/joc.1175 (  0) 0) |
Tolman, H. L., 2011. A conservative nonlinear filter for the highfrequency range of wind wave spectra. Ocean Modelling, 39: 291-300. DOI:10.1016/j.ocemod.2011.05.004 (  0) 0) |
Tolman, H. L., 2013. A generalized multiple discrete interaction approximation for resonant four-wave nonlinear interactions in wind wave models with arbitrary depth. Ocean Modelling, 70: 11-24. DOI:10.1016/j.ocemod.2013.02.005 (  0) 0) |
Uppala, S. M., KÅllberg, P. W., Simmons, A. J., Andrae, U., Da Costa Bechtold, V. and Fiorino, M., et al, 2006. The ERA-40 reanalysis. Quarterly Journal of the Royal Meteorological Society, 131: 2961-3012. (  0) 0) |
Vosough, A., 2011. Wave power. International Journal of Multidisciplinary Sciences and Engineering, 2(7): 60-63. (  0) 0) |
Wan, Y., Zhang, J., Meng, J. M. and Wang, J., 2015. A wave energy resource assessment in the China's seas based on multisatellite merged radar altimeter data. Acta Oceanologica Sinica, 34(3): 115-124. DOI:10.1007/s13131-015-0627-6 (  0) 0) |
Wan, Y., Zhang, J., Meng, J. M., Wang, J. and Dai, Y. S., 2016. Study on wave energy resource assessing method based on al-timeter data – A case study in Northwest Pacific. Acta Ocean-ologica Sinica, 35(3): 117-129. DOI:10.1007/s13131-016-0804-2 (  0) 0) |
Widén, J., Carpman, N., Castellucci, V., Lingfors, D., Olauson, J., Remouit, F., Bergkvist, M., Grabbe, M. and Waters, R., 2015. Variability assessment and forecasting of renewables: A review for solar, wind, wave and tidal resources. Renewable and Sustainable Energy Reviews, 44: 356-375. (  0) 0) |
Yan, Z. D., Liang, B. C., Wu, G. X., Wang, S. Q. and Li, P., 2019. Ultra-long return level estimation of extreme wind speed based on the deductive method. Ocean Engineering, 197: 106900. DOI:10.1016/j.oceaneng.2019.106900 (  0) 0) |
Zheng, C. W. and Li, C. Y., 2017a. Propagation characteristic and intraseasonal oscillation of the swell energy of the Indian Ocean. Applied Energy, 197: 342-353. DOI:10.1016/j.apenergy.2017.04.052 (  0) 0) |
Zheng, C. W. and Li, C. Y., 2017b. Analysis of temporal and spatial characteristics of waves in the Indian Ocean based on ERA-40 wave reanalysis. Applied Ocean Research, 63: 217-228. DOI:10.1016/j.apor.2017.01.014 (  0) 0) |
Zheng, C. W. and Li, C. Y., 2018. An overview and suggestions on the difficulty of site selection for marine new energy power plant – wave energy as a case study. Journal of Harbin Engineering University, 39(2): 200-206. (  0) 0) |
Zheng, C. W., Li, C. Y. and Pan, J., 2018. Propagation route and speed of swell in the Indian Ocean. Journal of Geophysical Research: Oceans, 123: 8-21. DOI:10.1002/2016JC012585 (  0) 0) |
Zheng, C. W., Lin, G. and Shao, L. T., 2013. Frequency of rough sea and its long-term trend analysis in the China Sea from 1988 to 2010. Journal of Xiamen University (Natural Science), 52(3): 395-399. (  0) 0) |
Zheng, C. W., Shao, L. T. and Shi, W. L., 2014b. An assessment of global ocean wave energy resources over the last 45 a. Acta Oceanologica Sinica, 33(1): 92-101. DOI:10.1007/s13131-014-0418-5 (  0) 0) |
Zheng, C. W., Zhou, L., Song, S. and Pan, J., 2014a. Simulation of the wave field caused by 1307 typhoon 'Soulik'. Journal of Xiamen University (Natural Science), 53(2): 257-262. (  0) 0) |
Zheng, C. W., Zhuang, H., Li, X. and Li, X. Q., 2012. Wind energy and wave energy resources assessment in the East China Sea and South China Sea. Science China Technological Sciences, 55(1): 163-173. DOI:10.1007/s11431-011-4646-z (  0) 0) |
Zhou, L. M., Wu, L. Y., Guo, P. F. and Wang, A. F., 2007. Simulation and study of wave in South China Sea using WAVE-WATCH-Ⅲ. Journal of Tropical Oceanography, 26(5): 1-8. (  0) 0) |
Zhou, L., Mei, Y., Wang, H. J. and Zheng, C. W., 2011. Interdecadal variations of sea surface wind and significant wave height in the North Indian Ocean and South China Sea. Transactions of Atmospheric Sciences, 34(5): 547-554. (  0) 0) |
Zhou, Z. L. and Yang, X. Y., 2008. Numberical simulation of wave filed in South China Sea using WWATCH-Ⅲ. Journal of Tropical Oceanography, 27(2): 1-6. (  0) 0) |
 2021, Vol. 20
2021, Vol. 20


