2) Institute of Coastal Research, Ludong University of China, Yantai 264025, China;
3) Yantai Kekan Marine Technology Co., Ltd., Yantai 264025, China;
4) Yantai Marine Environment Monitoring Center Station of SOA, Yantai 264006, China;
5) Yantai Yuan Shengda Marine Science and Technology Co., Ltd., Yantai 264006, China
The storm surge level comprises four primary components: the astronomical tide level, the typhoon's low pressure, the typhoon's wind field, and the water level increase caused by wave action. Since the 1950s, storm surge prediction models have ignored the water level increase caused by wave action, referred to as 'wave storm water', to improve calculation speed (Fernandez-Montblanc et al., 2018; Pan and Liu, 2019). Storm surge occurs when abnormal sea surface elevation results from weather systems such as tropical cyclones, temperate cyclones, or cold fronts, which bring strong winds and drastic changes in air pressure. When storm surge combines with astronomically high tides, it elevates sea levels, leading to a surge in tide levels in nearshore waters, affecting the safety of people living in coastal areas. Typhoon parameters such as intensity, path, radius, wind speed, air pressure, and movement speed affect the magnitude of water level changes caused by storm surges (Condon and Sheng, 2012; Kim et al., 2018; Fahim and Takagi, 2020).
In recent years, exacerbated by global warming, sea level rise has heightened the susceptibility of coastal areas to storm surge flooding and runoff, escalating the risk of storm surge disasters in coastal cities and potentially leading to severe losses (Liu and Huang, 2019). Data from the Joint Typhoon Warning Center spanning 1960 – 2021 reveal high incidences of storm surge in various regions, including the North Indian Ocean, the Northwest Pacific Ocean, and the Atlantic Gulf of Mexico coastal waters. These areas, characterized by specific geographic locations, climatic conditions, and marine environments, face severe threats to their coastlines and coastal communities because of storm surges. In the northern Indian Ocean, storm surges primarily occur in the northern Bay of Bengal, with a small amount of distribution in other areas of the bay and the Arabian Sea. The coastal areas of the Bay of Bengal are affected by the El Niño-Southern Oscillation, resulting in highly destructive and rapid surges (Bhardwaj et al., 2019). In the Northwest Pacific Ocean, storm surges concentrate in low-latitude areas like the Philippines, Malaysia, and Indonesia. These areas are often affected by newly formed typhoons and tropical cyclones because of their proximity to the equator (Zhang et al., 2015; Rodrigo et al., 2018; Muskananfola et al., 2020). The coastal areas along the Gulf of Mexico in the western Atlantic are susceptible to North Atlantic hurricanes, influenced by complex and variable marine environments shaped by factors such as warm and cold currents, and ocean currents. These environmental changes can alter water levels, increasing the likelihood of storm surges (Yao et al., 2017). Similarly, the eastern coastal region of China is one of the countries severely affected by storm surges, especially in the shallow waters, areas with poor coastal geography, and densely populated peninsular sea areas in the east. Every year, this region suffers from significant economic losses because of the impact of storm surges (Zhang et al., 2019).
Many countries have extensively researched storm surge disasters in the mentioned regions. The National Oceanic and Atmospheric Administration in the United States is dedicated to studying and monitoring storm surges. They utilize advanced ocean observation technologies such as satellite remote sensing and tide measurements for prediction and monitoring purposes. Additionally, the United States has established a storm surge warning system and implemented various defense measures, such as seawalls and coastal engineering (Needham and Keim, 2011; Elko et al., 2021). China is also actively studying storm surge disasters. Institutions like the Coastal Zone Research Institute of the Chinese Academy of Sciences, the Seismological Bureau, and the Oceanic Bureau have conducted extensive research to improve storm surge prediction and early warning capabilities. In addition, China has strengthened its defense measures by building seawalls and enhancing marine monitoring systems. Japan, situated in the western Pacific and frequently impacted by typhoons, prioritizes the study of storm surges (Wang et al., 2021a). The Japan Meteorological Agency uses advanced meteorological radar and satellite technology to monitor storm surges and provide accurate warning information. Japan has also strengthened its ocean observation network and implemented various defensive measures like reinforcing seawalls and building floodgates (Kim et al., 2020). European countries are actively studying storm surge disasters as well. Institutions such as the European Joint Research Centre use advanced numerical models and remote sensing technology to predict storm surges (Koutrakis et al., 2011; Vousdoukas et al., 2016). In addition, Europe has strengthened its ocean monitoring network and undertaken defensive measures such as building seawalls and embankments. Overall, various countries have made significant progress in the research and defense against storm surge disasters. Utilizing advanced observation techniques, numerical models, and strengthening defense measures can enhance the ability to predict and mitigate storm surges' impact on human lives and property (Trégarot et al., 2021). Fu et al. (2018) analyzed the impact of different cyclone types on storm surges in the Yellow and Bohai Seas. Although the article used the coastal propagation model of Kelvin waves to explain the timing of maximum storm surge, it did not quantitatively analyze the maximum storm surge in various coastal areas. Current research indicates a relatively weak understanding of the specific mechanisms and influencing factors of storm surge formation in the Yellow and Bohai Seas. In-depth exploration of the formation mechanisms of storm surges and quantitative analysis of their impact on water level rise in various coastal areas are necessary (Fu et al., 2018).
At present, most scholars focus on analyzing storm surge and water level rise in peninsular areas near low-latitude open bays or deep oceans, with limited attention given to semi-closed bays of the Bohai Sea in the northern middle and high latitudes of the Shandong Peninsula. For instance, Kim et al. (2018) used the SWAN model to simulate Typhoon No. 1215 Bolaven on the Korean Peninsula, evaluating the impact of different waveforms on storm surge. They conducted a comparative analysis of various input waveforms using the same model to assess their effect on storm surges (Kim et al., 2018). Medellin et al. (2021) investigated the impacts of different landfalls, slopes, and conditions on the storm surge in the Yucatan Peninsula near the Gulf of Mexico, considering factors such as slopes, sandbars, berms, and dunes (Medellin et al., 2021; Trégarot et al., 2021). Pattanayak et al. (2016) used the one-way coupling of the NMM-WRF model with the storm surge pattern of the IITD model to enhance storm surge prediction before typhoon landfall in the Bay of Bengal. They analyzed the evolution of the storm surge over time in the Bay of Bengal near the typhoon's landfall site. Existing studies primarily focus on water level increases in offshore areas or estuaries under different typhoon paths (Pattanayak et al., 2016). Casualties and direct economic losses resulting from storm surges in the Yellow and Bohai Sea areas are mainly concentrated in the Shandong Peninsula, with the proportion of disaster losses in these areas increasing over the past decade. Considering the recent possibility of storm surge warning tide level values triggering a red alert, coastal areas of Shandong have inadequate anti-surge capabilities and weak storm surge awareness. As the Shandong Peninsula is an important economic region and population center in the eastern coastal area of China, conducting research on the mechanisms of storm surge disasters and establishing a risk assessment system in this region are crucial. However, in-depth analysis of water level rise in offshore areas when typhoons with different paths make landfall and then leave the country is lacking. This study aims to address this gap by simulating typhoon data using measured station data from the northern Shandong Peninsula. Following verification of simulation and measured data, the study explores the impacts on the Shandong Peninsula under different typhoon routes without altering wind speed and direction. This research aims to provide a scientific basis for early warning and prediction of future marine disasters in offshore areas affected by similar strong typhoons.
2 Regional Overview 2.1 Study AreaThe Shandong Peninsula, situated on the eastern coast of China, is bordered by the Bohai Sea to the north and the Yellow Sea to the south. It is a crucial shipping hub and is home to several renowned coastal tourist cities (Dalledonne and Mayerle, 2016; Wang et al., 2021b). Each year, during the peak summer tourism season, many typhoons occur, resulting in substantial economic losses. Therefore, studying storm surge water level rise along the Shandong Peninsula is of paramount importance. Such research not only enhances the accuracy of storm surge disaster prediction and provides reliable references for related regions but also holds essential significance for storm surge prevention and mitigation efforts in the Shandong Peninsula sea area.
To conduct a comprehensive study on storm surge in the waters of the Shandong Peninsula during typhoon periods, this research selected several observation stations: the Zhifu Island tidal station in the northern part of Yantai, the Xiaoshi Island tidal station in the northern part of Weihai, the Shidao Island tidal station in the eastern part of Rongcheng in Weihai, and the No. 7 wind station buoy in Sanggou Bay. These stations are strategically located near urban areas and serve as reliable references for storm surge disaster forecasting. The locations of these observation stations are shown in Fig.1 below.

|
Fig. 1 Typhoon 1909 Lekima typhoon path and location of measuring points. |
Typhoon Lekima originated in the Northwest Pacific Ocean on August 4, 2019. It made landfall at 1:45 a.m. on the 10th in Zhejiang Province, with maximum wind speeds reaching 52 m s−1 and the lowest central pressure recorded at 930 hPa. Subsequently, Lekima moved northward and weakened gradually. However, it regained strength upon reentering the water near Lianyungang City, Jiangsu Province, and made another landfall at 8:50 p.m. on August 11 in Qingdao, Shandong. The maximum wind speed near the center was 23 m s−1, with the minimum central pressure recorded at 980 hPa. Following this, Lekima continued its northward trajectory. Influenced by the combined effect of continental high pressure and subtropical high pressure, it lingered south of Laizhou Bay for approximately 20 h. As the intensity of the subtropical high decreased, Lekima moved northward toward the southern part of the Bohai Sea and transformed into a tropical low-pressure system. It then followed a swirling path over the northern sea area of the Shandong Peninsula before moving to the Bohai Sea region, thereby concluding its impact on the Shandong region (Chen et al., 2021; Xu et al., 2021; Zhao et al., 2021). Fig.1 shows the changes in wind speed levels during the movement of Typhoon Lekima. For instance, wind speeds gradually increased from the typhoon's formation on August 9, 2019, at 4 a.m., reaching their peak before gradually diminishing near the Shandong Peninsula. The basic situation during the movement of the typhoon is shown in Table 1.
|
|
Table 1 Basic information on Typhoon 1909 Lekima |
Measuring the height of the tide is an important method for measuring the magnitude of storm surges. Various approaches exist for tide measurement, including establishing tide gauge stations on land and deploying tide gauges in the sea. Considering the continuity, reliability, and consistency of hydrological data, this study primarily focuses on deploying tide gauges in the sea. These tide gauges collect data at intervals of 10 minutes, with a month as the basic observation period. Additionally, most tide gauges commonly use pressure sensors. Finally, during data extraction, adjustments should be made on the basis of local atmospheric pressure changes.
Data regarding typhoon paths is sourced from the Tropical Cyclone Data Center of the China Meteorological Administration. The latest climate reanalysis data (ERA5) provided by ECMWF is used as the background wind field. ERA5 effectively simulates surface wind field conditions over the ocean. However, conventional wind field products (ECMWF, CMCC) encounter difficulties in accurately representing the extreme wind speeds at the center of typhoons. To address this limitation and achieve precise simulation of the typhoon wind field, a high-precision typhoon model wind field capable of replicating actual typhoon wind speeds is integrated with the reanalysis wind field to obtain a high-resolution wind field.
3 Numerical Model 3.1 Delft 3DDelft 3D is an open-source hydrodynamic and river sediment modeling system developed by Delft University of Technology in the Netherlands. It is widely employed for studying and simulating hydrodynamic processes, waves, sediment transport, water quality, and ecosystems in rivers, estuaries, harbors, and coastal waters (Rautenbach et al., 2019).
The Delft 3D modeling system comprises several modules that can be selected and combined to simulate various hydrodynamic processes. This study mainly uses its Wave and Flow modules, which utilize incompressible fluid assumptions, hydrostatic pressure assumptions, and Boussinesq assumptions. We employ the alternating implicit method (ADI) numerical computation to solve the Reynolds-averaged Navier-Stokes equations. This method is known for its high computational speed, stability, and accuracy (Feng et al., 2020).
Simultaneous equations:
| $ \frac{\partial \zeta}{\partial t}+\frac{1}{\sqrt{G_{\xi \xi}} \sqrt{G_{\eta \eta}}} \frac{\partial\left((d+\zeta) U \sqrt{G_{\eta \eta}}\right)}{\partial \xi}+ \\ ~~~~~~\frac{1}{\sqrt{G_{\xi \xi}} \sqrt{G_{\eta \eta}}} \frac{\partial\left((d+\zeta) V \sqrt{G_{\xi \xi}}\right)}{\partial \eta}=(d+\zeta) Q, $ | (1) |
| $ U =\frac{1}{d+\zeta} \int_{d}^{\zeta} u \mathrm{d} z=\int_{-1}^{0} u \mathrm{~d} \sigma V\text{,} $ | (2) |
| $ V =\frac{1}{d+\zeta} \int_{d}^{\zeta} v \mathrm{d} z=\int_{-1}^{0} v \mathrm{d} \sigma, $ | (3) |
| $ Q=\int_{-1}^0\left(q_{\text {in }}-q_{\text {out }}\right) \mathrm{d} \sigma+P-E . $ | (4) |
The average velocities of direction ξ and direction η in the curved coordinate system in the model are U and V; Q is the change in quantity caused by evaporation, inflow, outflow or precipitation of water per unit area in the ocean; E and P is the amount of rainfall and evaporation, respectively; qin and qout is the amount of water inflow and outflow per unit volume, respectively; $\sqrt{G_{\zeta \zeta}}$ and $\sqrt{G_{\eta \eta}}$ is the transformation systems of x and y in the curvilinear coordinate system in the ξ direction and in the η direction in the right-angled coordinate system, respectively.
Dynamical equation in the ξ direction and momentum equation in the η direction:
| $ \begin{align*} \frac{\partial u}{\partial t}+ & \frac{u}{\sqrt{G_{\xi \xi}}} \frac{\partial u}{\partial \xi}+\frac{v}{\sqrt{G_{\eta \eta}}} \frac{\partial u}{\partial \eta}+\frac{\omega}{d+\zeta} \frac{\partial u}{\partial \sigma}-\frac{v^{2}}{\sqrt{G_{\xi \xi}} \sqrt{G_{\eta \eta}}} \frac{\partial \sqrt{G_{\eta \eta}}}{\partial \xi}+\frac{u v}{\sqrt{G_{\xi \xi}} \sqrt{G_{\eta \eta}}} \frac{\partial \sqrt{G_{\xi \xi}}}{\partial \eta}-f v= \\ & -\frac{1}{\rho_{0} \sqrt{G_{\xi \xi}}} P_{\xi}+F_{\xi}+\frac{1}{(d+\zeta)^{2}} \frac{\partial}{\partial \sigma}\left(v_{V} \frac{\partial u}{\partial \sigma}\right)+M_{\xi} , \end{align*}$ | (5) |
| $ \begin{align*} \frac{\partial v}{\partial t}+ & \frac{v}{\sqrt{G_{\xi \xi}}} \frac{\partial v}{\partial \xi}+\frac{v}{\sqrt{G_{\eta \eta}}} \frac{\partial u}{\partial \eta}+\frac{\omega}{d+\zeta} \frac{\partial v}{\partial \sigma}-\frac{u^{2}}{\sqrt{G_{\xi \xi}} \sqrt{G_{\eta \eta}}} \frac{\partial \sqrt{G_{\eta \eta}}}{\partial \xi}-\frac{u v}{\sqrt{G_{\xi \xi}} \sqrt{G_{\eta \eta}}} \frac{\partial \sqrt{G_{\xi \xi}}}{\partial \eta}-f u \\ & =-\frac{1}{\rho_{0} \sqrt{G_{\eta \eta}}} P_{\eta}+F_{\eta}+\frac{1}{(d+\zeta)^{2}} \frac{\partial}{\partial \sigma}\left(v_{V} \frac{\partial v}{\partial \sigma}\right)+M_{\eta}.\end{align*} $ | (6) |
The flow velocities in the η and ξ directions in the model are v and u, respectively; the parameter of the Kohl's force is f; ω represents the vertical velocity of the sigma in the coordinate system of the model; υV is the viscous coefficient of the turbulence in the vertical direction in the coordinate system; and ρ0 is the density of the water in the ocean. The gradient of the hydrostatic pressure in the ξ and η directions in the coordinate system is specified as Pξ and Pη, respectively; the turbulent momentum fluxes in the model are Fξ (in ξ direction) and Fη (in η direction), respectively; and the source and sink terms of momentum are Mη (in η direction) and Mξ (in ξ direction), respectively.
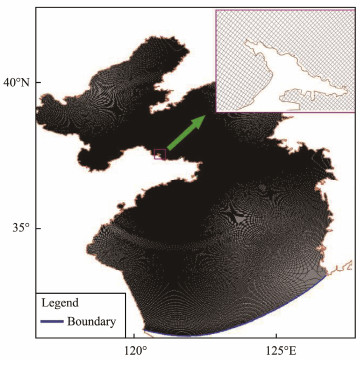
3.2 Model CouplingTo ensure accurate storm surge calculations, numerical simulations must cover a vast expanse of the ocean. Given the extensive area of the Shandong Peninsula sea region, nested grids are not needed in simulation calculations. The computation range of this grid spans from 117.6˚E to 126.5˚E longitude and 32.5˚N to 40.8˚N latitude, encompassing most of the Bohai Sea and the Yellow Sea, totaling 158592 grids. The resolution of the boundary grids is set at 3.3 km. As shown in Fig.2, the highest grid resolution along the coast of the Shandong Peninsula reaches 60 m. All depth data are sourced from electronic charts.
|
Fig. 2 Calculation area and grid. |
Initial condition: ζ = µ = ν = 0.
Closed boundary condition: Free slip boundary conditions are adopted. That is, the shear stress on the shoreline closed boundary is 0.
Open boundary condition: The Delft 3D model provides 8 main tidal harmonic constants, namely M2, N2, S2, K2, K1, O1, P1, and Q1, as driving forces on the open boundary. Tidal harmonic constants are taken from the global tidal model TPXO7.2.
1) Typhoon wind field production
The maximum wind speed radius R is calculated using the Willoughby and Rahn (WR) formula, which is given in Eq. (7).
| $ \begin{equation*} R=5.16 \exp \left(-0.0223 V_{\max }+0.0281|\varphi|\right) \end{equation*}. $ | (7) |
The Vmax value is the maximum wind speed of the typhoon, and the φ value is the latitude of the typhoon center.
To accurately calculate the symmetric wind field at the center of the typhoon, different calculation formulas are used in accordance with the distance r from the center of the typhoon and twice the maximum wind speed radius R. When the distance from the center of the typhoon is less than or equal to twice the maximum wind radius, Eqs. (8) and (9) are applied. Conversely, when the distance from the center of the typhoon exceeds twice the maximum wind radius, Eqs. (10) and (11) are employed for calculation, as follows:
| $ \begin{gathered} W_{x}=C_{1} V_{x} \exp \left(-\frac{\pi}{4} \cdot \frac{|r-R|}{R}\right)-C_{2}\left\{-\frac{f}{2}+\sqrt{\frac{f^{2}}{4}+10^{3} \frac{2 \Delta P}{\rho_{a} R^{2}}\left[1+2\left(\frac{r^{2}}{R^{2}}\right)\right]^{-3 / 2}}\right\} \cdot\left[\left(x-x_{0}\right) \sin \theta+\left(y-y_{0}\right) \cos \theta\right]\text{,} \\ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~0 \leq r \leq 2 R, \end{gathered} $ | (8) |
| $ W_{y}=C_{1} V_{y} \exp \left(-\frac{\pi}{4} \cdot \frac{|r-R|}{R}\right)+C_{2}\left\{-\frac{f}{2}+\sqrt{\frac{f^{2}}{4}+10^{3} \frac{2 \Delta P}{\rho_{a} R^{2}}\left[1+2\left(\frac{r^{2}}{R^{2}}\right)\right]^{-3 / 2}}\right\} \cdot\left[\left(x-x_{0}\right) \cos \theta-\left(y-y_{0}\right) \sin \theta\right], \\ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 0 \leq r \leq 2 R, $ | (9) |
| $ \begin{array}{l} {W_x} = {C_1}{V_x}\exp \left({ - \frac{\pi }{4} \cdot \frac{{|r - R|}}{R}} \right) - {C_2}\left\{ { - \frac{f}{2} + \sqrt {\frac{{{f^2}}}{4} + {{10}^3}\frac{{\Delta P}}{{{\rho _a}{{(1 + r/R)}^2}Rr}}} } \right\} \cdot \left[ {\left({x - {x_0}} \right)\sin \theta + \left({y - {y_0}} \right)\cos \theta } \right] ,\\ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 2R < r < \infty, \end{array} $ | (10) |
| $ \begin{equation*} W_{y}=C_{1} V_{y} \exp \left(-\frac{\pi}{4} \cdot \frac{|r-R|}{R}\right)+C_{2}\left\{-\frac{f}{2}+\sqrt{\frac{f^{2}}{4}+10^{3} \frac{\Delta P}{\rho_{a}(1+r / R)^{2} R r}}\right\} \cdot\left[\left(x-x_{0}\right) \cos \theta-\left(y-y_{0}\right) \sin \theta\right],\\ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 2R < r < \infty. \end{equation*} $ | (11) |
Wx and Wy are the wind speed situation in the x and y directions, respectively. Vx and Vy represent the velocity component situation in both directions while the typhoon moves. It is the ratio of the typhoon's moving distance to the time. ∆P = P∞ − P0. R is the radius of the maximum wind speed, r is the distance from the center of the typhoon, and the units of radius are all centimeters. f is the Kurtosis force, ρa is the air density, θ is the inflow angle, and the parameterization is set to 17.5. C1 and C2 are taken as constants, with C1 being set to 0.8 and C2 set to 1.
2) Synthetic wind field production
After obtaining a high-precision typhoon model wind field that can reach the actual wind speed of the typhoon, it is combined with the reanalyzed wind field so that a high-resolution wind field can be obtained. The synthesis formula is as follows:
| $ \begin{equation*} V=(1-e) V_{m}+e V_{e}, e=\frac{c}{1+c^{4}}, c=\frac{r}{n R}, \end{equation*} $ | (12) |
where V is the final synthesized wind field; Vm is the modeled wind field that can reach the actual wind speed; Ve is the background wind field processed by the reanalysis; r and R is the distance of the typhoon to the simulation point and the radius of the maximum wind speed of the typhoon, respectively; and n is a constant, set as 1.
3.3 Model Parameter ConfigurationThe storm surge model simulation duration spans from August 3, 2019, 18:00, to August 14, 2019, 12:00, with a simulation time step of 1 min. The underwater terrain near the observation station in the model is derived from actual measurements and interpolation, whereas the underwater terrain in other areas is sourced from ETOP data. Considering potential variations in wind speed across different areas, the model uses wind field data downloaded from ERA5, featuring a spatial resolution of 0.1˚ × 0.1˚ and a temporal resolution of hourly intervals. The constant value for gravity acceleration in the physical parameters is 9.81 m s−2. For bottom roughness representation, the model uses the Manning coefficient, set to 0.017 s m−1/3. Additionally, the horizontal eddy viscosity coefficient is configured to 15 m2 s−1. Other parameters for various paths are specified, as shown in Table 2.
|
|
Table 2 Elements of Typhoon Lekima panning |
To assess the accuracy of the Delft 3D storm surge model, this study uses Willmott's statistical method and the Pearson correlation coefficient method to evaluate the model results. The calculation formula for Willmott is as follows:
| $ \begin{equation*} r=1-\frac{\sum\limits_{i=1}^{n}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{\sqrt{\sum\limits_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}} \sqrt{\sum\limits_{i=1}^{n}\left(Y_{i}-\bar{Y}\right)^{2}}}, \end{equation*} $ | (13) |
where Xi and Yi are the calculated values of the model, X and Y are the measured values, and X and Y are the average measured values. The skill value indicates the correlation between the model's simulated value deviation from the average measured value and the deviation of the measured value from the average. It ranges from 0 to 1, with a skill value of 1 indicating no difference between the model's simulation and measured values. A skill value exceeding 0.65 is considered excellent, while a value between 0.65 and 0.5 is very good. A value between 0.5 and 0.2 is considered good, and a value less than 0.2 is poor. A skill value of 0 indicates complete inconsistency between the calculated and measured values.
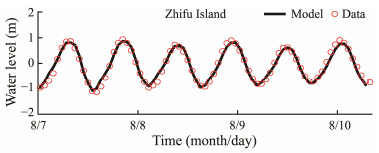
4 Numerical Model Validation 4.1 Verification of Astronomical Tide LevelAccurate simulation of astronomical tides is a prerequisite for the numerical simulation of typhoon storm surges (Chen et al., 2017). This study selects measured tidal data from the Zhifu Island Shandong Coastal Tidal Station (37.6˚N, 121.4˚E) in August 2019 as verification data for astronomical tides. The measured wind field data from the No. 7 wind station buoy (37.1˚N, 122.6˚E) is used to verify the model's wind speed. The model calculates the tidal process solely under the influence of astronomical tides and compares it with the measured data. The verification results show a satisfactory agreement between the two datasets, with the simulation accurately capturing changes in water level and high and low tides. The calculated correlation coefficient for Zhifu Island's water level is 0.96. Fig.3 shows the validation of astronomical tide level in Zhifu Island.
|
Fig. 3 Verification of astronomical tide level in Zhifu Island. |
This time, the No. 7 wind station buoy, impacted by Typhoon Lekima on the Shandong Peninsula, is selected to verify the data measured by the meteorological station and the typhoon wind speed calculated by the previous model. The positioning of the No. 7 buoy wind station is shown in Fig.4. This station measures the typhoon wind speed, which is the average wind speed recorded every ten minutes by the anemometer. Upon comparison, the simulation and actual measurement generally exhibit similar extreme values. Although the peak value of the calculated wind speed is slightly higher than that of the measured wind speed, the overall increasing or decreasing trend aligns well. These results show that the wind field constructed in this study can effectively replicate the process of wind speed change during the passage of Typhoon Lekima over the Shandong Peninsula. The wind field of this typhoon can be used as a simulation of the wind stress field for storm surge.

|
Fig. 4 Verification of wind speed at No. 7 Buoy station. |
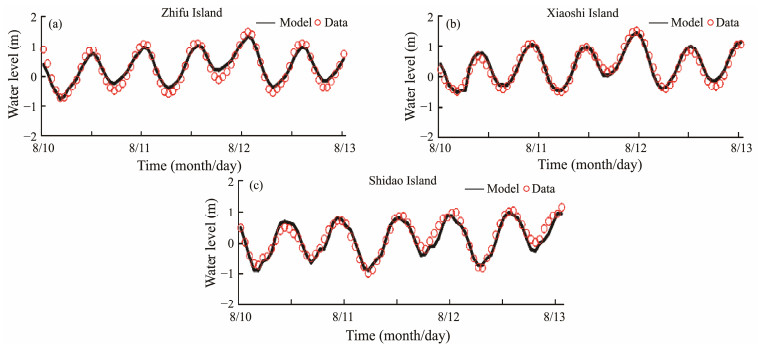
Fig.5 shows that the simulated storm surge process caused by Typhoon Lekima aligns well with the actual measured process. Table 3 presents the error statistics for each station. Zhifu Island, Xiaoshi Island, and Shidao Island exhibit correlation coefficients of 0.95, 0.98, and 0.96, respectively, for tidal water levels. The average absolute error for the maximum water level at each station is 0.19 m, with a maximum error value of 0.30 m. The relative error between the model results and the measured data for all three stations is less than 10%. The accurate verification of the model and tidal results confirms the rationality of the model settings, wind field data, boundary conditions, and other parameters. The results lay a solid foundation for comparing future storm surge simulations under various meteorological conditions. And this model can be used to study the storm surge generated by typhoon path.
|
Fig. 5 Validation of storm water augmentation. |
|
|
Table 3 Maximum storm water error statistics for each station triggered by the typhoon |
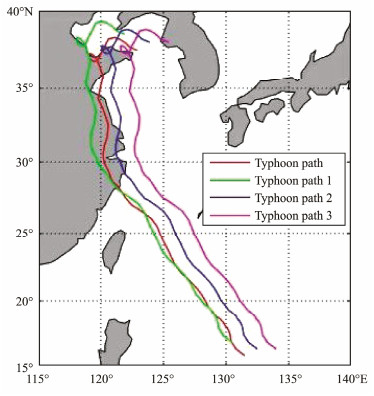
As typhoons exert the most significant impact on coastal regions, the landing point after shifting the typhoon path is confined within the boundaries of a coastal city. This study uses the path of Typhoon Lekima as a reference, solely shifting the typhoon's path without changing any other parameters. Three scenarios of the typhoon path have been designated. Considering that the original route of the typhoon traversed the Shandong Peninsula before looping back in the coastal area, the loop point is also positioned in the coastal area during the path translation. Specifically, the typhoon is set to make landfall separately in Rizhao Lanshan, Yantai Haiyang, and Weihai Rongcheng on the Shandong Peninsula. The typhoon paths after translation can be seen in Fig.6.
|
Fig. 6 Derivative path of Typhoon Lekima. |
The storm surge value depicted in the Fig.7 is derived by subtracting the astronomical tide value at the corresponding time from the validated tidal level at that point. To comprehensively examine the storm surge situation at typical stations during four typhoon paths, this study analyzes the storm surge situation at the three validated points mentioned above during the four typhoon events. The statistical change of water level augmentation at typical stations is shown in Table 4.
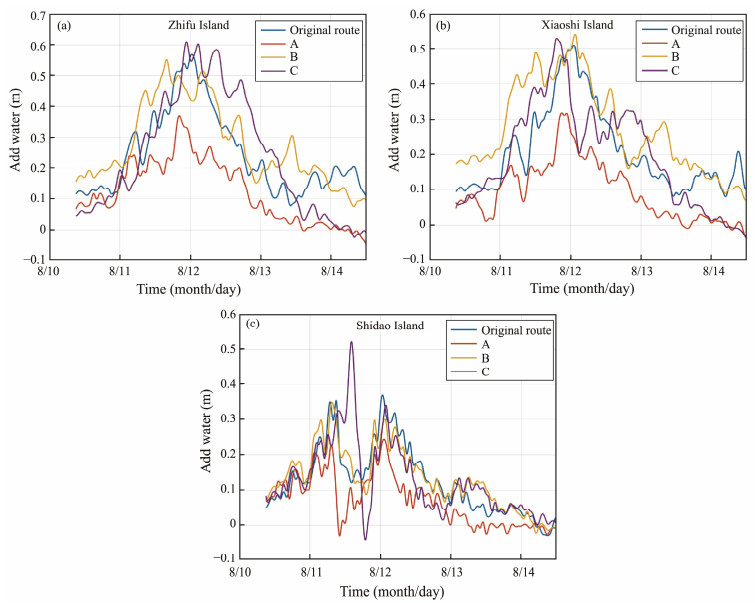
|
Fig. 7 Storm water at typical stations under various typhoon paths. |
|
|
Table 4 Statistical table of changes in water augmentation at typical stations |
Upon comparison, the maximum increase in water level for all three scenarios occurred around 00:00 on August 12, with little deviation from the time of maximum storm surge level along the original path. Subsequent to the storm surge, there is a slight reduction in water level, averaging around 0.1 m. The storm surge values for scenario B and the original route are essentially identical. Specifically, the maximum storm surge at the Xiaoshi Island tide gauge station transpired around 00:00 on August 12 in scenario B, reaching approximately 0.53 m. Scenario B exhibits a maximum storm surge level akin to the original path, although the overall storm surge volume surpasses that of the original route.
Similarly, the maximum storm surge at the Zhifu Island tide gauge station materialized around 8 p.m. on August 11 in scenario C, with a maximum storm surge level of about 0.60 m. Multiple peaks were evident in the maximum increase, and the storm surge did not significantly differ from that of the original route.
By contrast, the storm surge level at the Shidao Island tide gauge station presents distinctive characteristics. Prior to 9:00 a.m. on August 11, the water level at the Shidao Island station exhibited a gradual increase, followed by a rapid decrease until a low tide occurred around 12:00 a.m. on August 12. Subsequently, the water level returned to the average level. This phenomenon may be attributed to the unique geographical location of the Shidao Island Station, situated in a semi-enclosed bay in the easternmost part of the Shandong Peninsula, resembling the shape of a trumpet and opening to the south.
Furthermore, the impact time of different typhoon paths on different stations varies. Considering a storm surge exceeding 20 cm as the benchmark for storm surge warning, the disparities in the storm surge impact on Xiaoshi Island and Zhifu Island are most notable across different paths. The impact time of path A is the shortest, approximately 12 h, whereas the impact time of path B is the longest, lasting about 54 h. The impact time of the original path and path C does not vary much. The impact time of Shidao Island remains relatively consistent for all paths, hovering around 24 h.
5.3 Spatial Distribution of Storm Surge AugmentationAs shown in Fig.8, the storm surge exhibits apparent asymmetry on both sides of the typhoon center. Generally, the wind speed is higher on the side of the typhoon adjacent to a high-pressure system, but it is lower on the side closer to a low-pressure system as the typhoon moves. Therefore, when a typhoon moves from the southeast to the west (or northwest), the right side of the typhoon's path typically experiences stronger winds because of its proximity to the subtropical high pressure in the western Pacific, whereas the left side encounters weaker winds. The magnitude of the storm surge is directly correlated with the difference in pressure between the center of the typhoon or low-pressure system and its surroundings. As the central pressure drops, the sea level rises, resulting in the asymmetry of the storm surge on both sides of the typhoon's path.

|
Fig. 8 Spatial map of maximum storm water in the original scenario and typhoon paths A, B, and C. |
From 12:00 on August 11 to 12:00 on August 13, during the astronomical tide, which coincided with the period of Typhoon Lekima having the most substantial impact on the Shandong Peninsula, the model calculated the maximum storm surge temporal and spatial data by subtracting the astronomical tide value without the typhoon from the numerical value of the tide level in each grid during this period.
At this juncture, in the aforementioned three scenarios, the peripheral area of Typhoon Lekima is situated in the surrounding waters of the Shandong Peninsula. Nonetheless, the storm surge range will persistently shift northward with the typhoon's center. The spatial distribution of the storm surge remains relatively consistent across the three paths mentioned above, with greater storm surge observed in the northern part of the peninsula compared with the southern part.
In scenario A, the maximum storm surge extends outward from Binzhou Port, reaching the vicinity of Yantai Penglai Port. These regions will encounter a significant increase in storm surges. Conversely, there will be a minor reduction in water level along the Shandong Peninsula coastline from Yantai Penglai Port to Rizhao Lanshan Port.
The spatial distribution of the storm surge level in scenario B is similar to that of scenario A. The main areas with storm surge levels are concentrated in the northwest coastal area of the Shandong Peninsula. The difference between the two scenarios is that scenario B's maximum storm surge level shifts eastward with the typhoon's path, and the maximum storm surge level appears near Laizhou Bay. The center of the typhoon's path passes through the Yantai surrounding sea in the central part of the Shandong Peninsula, so a significant storm surge is evident in that area.
In scenario C, the typhoon path spends more time over the sea, with only a portion of the path passing over land. Therefore, the storm surge is significantly reduced compared with the three scenarios mentioned above, and the affected areas are more scattered. Both the southern and northern parts of the Shandong Peninsula experience a small amount of storm surge.
5.4 Comparison of Maximum Storm Water Augmentation DistributionThe analysis of the three scenarios (A, B, and C) depicted in the above figure, illustrating the movement of Typhoon Lekima, reveals a close correlation between the distribution of maximum storm surge and the typhoon's path. The storm surge in the northern part of the peninsula is more pronounced compared with the southern part, with less storm surge observed in the Rizhao areas of the southern peninsula in scenarios A and B. The difference that leads to less storm surges in the Rizhao areas can be attributed to the location of the city of Rizhao, situated north of the typhoon's path. In the northern hemisphere, typhoons rotate counterclockwise. As the typhoon progresses along its path, Rizhao finds itself in close proximity to the path, resulting in a significant surge in storm surge levels.
In scenario B, the storm surge gradually diminishes from west to east in the northern part of the Shandong Peninsula. The maximum surge is recorded in the Laizhou Bay area, reaching a height of 1.2 m. The partial displacement of the typhoon's path has intensified the storm surge around the typhoon, thereby impacting the determination of the design high water level at the docks near the typhoon's path.
6 DiscussionIn recent years, the rapid development of science and improvement of hydraulic numerical models have spurred in-depth investigations into the mechanisms driving storm surge formation by scholars from various countries. For instance, Chittibabu and Rao (2011) used a high-resolution 2D model to simulate the temperate storm surge in Lake Winnipeg in central North America in October 2010 (Chittibabu and Rao, 2011). Their results show that storm surges in estuarine areas experience relative delays because of the influence of river inflows into the sea. Storm surges affect shallow seas and inland areas with lower water levels than open lake stations. Therefore, in the future, special attention should be paid to preventing storm surges near the open lake station.
Al Mohi et al. (2018) used models like SLOSH and CH3D to establish a numerical coupled model of bays and rivers along the Bay of Bengal coast in a 2D Cartesian coordinate system. They aimed to investigate the impact of rivers on storm surges in Bangladesh. Their simulation results reveal a notable influence of rivers on storm surges, with river mouths experiencing a decrease of approximately 20% in peak water levels. Thus, the impact of rivers on storm surges must be addressed. However, this study was based on data from April 1991, during the transitional period between spring and summer, when typhoon frequency, rainfall, and river discharge are relatively low and unstable. As a result, the model has certain limitations in predicting storm surges during the summer season (Al Mohit et al., 2018).
Huang et al. (2022) employed the Mike 21 software to calculate storm surges in the Yellow River Delta under different wind directions. Their results show that because of the topography, a northeast wind can elevate the risk of storm surges in the coastal areas of the Yellow River Delta. Consistently, scenario B in this study corroborates this finding, revealing that during storm surges, a northeast wind in the Yellow River mouth area leads to a surge height approximately 0.2 m higher than in other regions (Huang et al., 2022).
Building upon this research, future investigations can focus on examining the impact of river flows during storm surge events in the summer flood season, starting from estuaries into the sea. Such studies can provide a scientific basis for early warning systems concerning marine disasters in offshore waters.
7 ConclusionsBy simulating the storm surge caused by Typhoon Lekima along its original path and its shifted paths A, B, and C in the waters of the Shandong Peninsula, the following conclusions are obtained:
1) A 2D storm surge numerical model is established on the basis of Delft 3D hydrodynamic and WR formula typhoon models. The model's measured data and numerical simulation data are in good agreement.
2) The impact of Typhoon Lekima on Shandong Province is mainly from the northwest direction. The distribution of storm surge decreases from the center of the typhoon to the coast, and the storm surge on both sides of the typhoon center shows apparent asymmetry.
3) The practical wind speed values measured by the No. 7 buoy wind station basically match the actual data trend. The simulated maximum wind speed is in agreement with the measured maximum wind speed, with a slight margin of error. The wind field vector diagram and storm surge isopleth reveal that the highest storm surge is in agreement with the highest wind speed in the wind field.
4) The wind is moving in a counterclockwise direction around the center of the typhoon, resulting in an increase in storm surge in the northern region of the Shandong Peninsula and a decrease in storm surge in the southern region. The storm surge caused by the typhoon is not as strong on either side of the path, with the left side being more powerful than the right.
5) As Typhoon Lekima neared the shores of the Shandong Peninsula from the Pacific Ocean, the tide fluctuated between rising and falling at each measuring point. In the future, when a typhoon lands on the west coast of the Shandong Peninsula, extreme storm surges may occur near Binzhou Port. For typhoons landing on the east coast of the Shandong Peninsula, large peak storm surges will occur in Laizhou Bay.
The results of this study contribute to understanding the typical northwest-moving typhoon storm surge in the Shandong Peninsula and its surrounding sea areas. They can also provide a reference for the formulation of coastal typhoon and storm surge disaster reduction policies.
This study does not consider the influence of other factors on the typhoon's path though. For example, when Typhoon A's path passes through Shandong, the wind force will be different as it is deep inland. The wind force will drop sharply, so the expected movement path may not be reached. Therefore, future studies should take into account other factors when translating the typhoon path.
AcknowledgementsThis study is supported by the Yantai Science, Technology and Innovation Development Programme (Nos. 2023JCYJ094, 2023JCYJ097), and the Major Research Grant from the Natural Science Foundation of China (NSFC) (No. 42330406).
Author Contributions
All authors contributed to the research in the paper. Hongyuan Shi designed the study, analyzed the data, and wrote the paper; Yongkang Sun searched the literature, designed the study, analyzed the data, and reviewed first drafts and revisions; Jiwei Sun analyzed the data and painted the figures. Longsheng Li, Shengnian Zhao, Haixia Wang and Xiaofan Yuan designed the study and searched the literature. Xin Hong and Qingjie Li carried out data measurement and model setting. All authors have read and agreed to the published version of the manuscript.
Data Availability
All data generated and analyzed during this study are included in this published article and its additional files.
Declarations
Ethics Approval and Consent to Participate
This article does not contain any studies with human participants or animals performed by any of the authors.
Consent for Publication
Informed consent for publication was obtained from all participants.
Conflict of Interests
The authors declare that they have no conflict of interests.
Al Mohit, M. A., Yamashiro, M., Hashimoto, N., Mia, M. B., Ide, Y., and Kodama, M., 2018. Impact assessment of a major river basin in Bangladesh on storm surge simulation. Journal of Marine Science and Engineering, 6(3): 99. (  0) 0) |
Bhardwaj, P., Pattanaik, D. R., and Singh, O., 2019. Tropical cyclone activity over Bay of Bengal in relation to El Niño-Southern Oscillation. International Journal of Climatology: A Journal of the Royal Meteorological Society, 39(14): 1-18. DOI:10.1002/joc.6165 (  0) 0) |
Chen, G., Zhang, X., Cao, Q., and Zeng, Z., 2021. Evaluation of forecast performance for Super Typhoon Lekima in 2019. Frontiers of Earth Science, 16(1): 17. (  0) 0) |
Chen, W. B., Lin, L. Y., Jang, J. H., and Chang, C. H., 2017. Simulation of typhoon-induced storm tides and wind waves for the northeastern coast of Taiwan using a tide-surge-wave coupled model. Water, 9(7): 549. DOI:10.3390/w9070549 (  0) 0) |
Chittibabu, P., and Rao, Y. R., 2011. Numerical simulation of storm surges in Lake Winnipeg. Natural Hazards, 60(2): 181-197. (  0) 0) |
Condon, A. J., and Sheng, Y. P., 2012. Optimal storm generation for evaluation of the storm surge inundation threat. Ocean Engineering, 43: 13-22. (  0) 0) |
Dalledonne, G. L., and Mayerle, R., 2016. Modelling of storm impacts on the Shandong Peninsula coast. Journal of Coastal Research, 74: 70-82. DOI:10.2112/SI74-007.1 (  0) 0) |
Elko, N., Briggs, T. R., Benedet, L., Robertson, Q., Thomson, G., Webb, B. M., et al., 2021. A century of U.S. beach nourishment. Ocean & Coastal Management, 199: 105406. (  0) 0) |
Fahim, M. R. I., and Takagi, H., 2020. Typhoon parameter sensitivity of storm surge in the semi-enclosed Tokyo Bay. Frontiers of Earth Science, 14(3): 553-567. (  0) 0) |
Feng, X., Dong, B., Ma, G., and Feng, W., 2020. Topographic and hydrodynamic influence on rip currents and alongshore currents on headland beaches in China. Journal of Coastal Research, 95: 468. (  0) 0) |
Fernández-Montblanc, T., Vousdoukas, M. I., Ciavola, P., Voukouvalas, E., Mentaschi, L., Breyiannis, G., et al., 2018. Towards robust pan-European storm surge forecasting. Ocean Modelling, 133: 129-144. (  0) 0) |
Fu, C. F., Yu, F. J., Wu, S. H., and Dong, J. X., 2018. Study on the characteristic of abnormal storm surge caused by cyclone in the Bohai Sea. Marine Forecasts, 35(1): 37-43. (  0) 0) |
Huang, L., Chen, S., Pan, S., Li, P., and Ji, H., 2022. Impact of storm surge on the Yellow River Delta: Simulation and analysis. Water, 14(21): 3439. (  0) 0) |
Kim, T. R., and Lee, J. H., 2018. Comparison of high wave hindcasts during Typhoon Bolaven (1215) using SWAN and WAVEWATCH Ⅲ Model. Journal of Coastal Research, 85: 1096-1100. (  0) 0) |
Kim, Y., Itoh, S., Oya, Y., and Yoon, J., 2018. Study on storm surge prediction model considering typhoon characteristics for largest scale. Journal of Coastal Research, 85: 736-740. (  0) 0) |
Kim, Y., Kim, T., and Yoon, J., 2020. Study on storm surge using parametric model with geographical characteristics. Water, 12(8): 2251. (  0) 0) |
Koutrakis, E., Sapounidis, A., Marzetti, S., Marin, V., Roussel, S., Martino, S., et al., 2011. ICZM and coastal defence perception by beach users: Lessons from the Mediterranean coastal area. Ocean & Coastal Management, 54(11): 821-830. (  0) 0) |
Liu, W. C., and Huang, W. C., 2019. Influences of sea level rise on tides and storm surge around the Taiwan coast. Continental Shelf Research, 173: 56-72. (  0) 0) |
Medellin, G., Mayor, M., Appendini, C. M., Cerezo-Mota, R., and Jiménez, J. A., 2021. The role of beach morphology and mid-century climate change effects on wave runup and storm impact on the northern Yucatan Coast. Journal of Marine Science and Engineering, 9: 518. (  0) 0) |
Muskananfola, M. R., Supriharyono, and Febrianto, S., 2020. Spatio-temporal analysis of shoreline change along the coast of Sayung Demak, Indonesia using digital shoreline analysis system. Regional Studies in Marine Science, 34: 101060. (  0) 0) |
Needham, H. F., and Keim, B. D., 2011. A storm surge database for the US Gulf Coast. International Journal of Climatology, 32(14): 2108-2123. (  0) 0) |
Pan, Z., and Liu, H., 2019. Extreme storm surge induced coastal inundation in Yangtze Estuary regions. Journal of Hydrodynamics, 31(6): 1127-1138. (  0) 0) |
Pattanayak, S., Mohanty, U. C., and Rao, A. D., 2016. Simulation of storm surge in the Bay of Bengal using one-way coupling between NMM-WRF and IITD storm surge model. Marine Geodesy, 39(5): 376-400. (  0) 0) |
Rautenbach, C., Barnes, M. A., and de Vos, M., 2019. Tidal characteristics of South Africa. Deep Sea Research Part Ⅰ: Oceanographic Research Papers, 150: 103079. (  0) 0) |
Rodrigo, S. M. T., Villanoy, C. L., Briones, J. C., Bilgera, P. H. T., Cabrera, O. C., and Narisma, G. T. T., 2018. The mapping of storm surge-prone areas and characterizing surge-producing cyclones in Leyte Gulf, Philippines. Natural Hazards, 92(3): 1305-1320. (  0) 0) |
Trégarot, E., Catry, T., Pottier, A., El-Hacen, E.-H. M., Ahmed Sidi Cheikh, M., Cornet, C. C., et al., 2021. Coastal protection assessment: A tradeoff between ecological, social, and economic issues. Ecosphere, 12(2): e03364. (  0) 0) |
Vousdoukas, M. I., Voukouvalas, E., Annunziato, A., Giardino, A., and Feyen, L., 2016. Projections of extreme storm surge levels along Europe. Climate Dynamics, 47(9-10): 3171-3190. (  0) 0) |
Wang, K., Yang, Y., Reniers, G., and Huang, Q., 2021a. A study into the spatiotemporal distribution of typhoon storm surge disasters in China. Natural Hazards, 108: 1237-1256. (  0) 0) |
Wang, N., Hou, Y., Mo, D., and Li, J., 2021b. Hazard assessment of storm surge and concomitant waves in Shandong Peninsula based on long-term numerical simulations. Ocean & Coastal Management, 213: 105888. (  0) 0) |
Xu, M., Li, H., Luo, J., Ben, H., and Zhu, Y., 2021. Predictability and dynamics of the rapid intensification of Super Typhoon Lekima (2019). Frontiers of Earth Science, 16(1): 12. (  0) 0) |
Yao, Z., Xue, Z., He, R., Bao, X., Xie, J., and Ge, Q., 2017. Climate projections of spatial variations in coastal storm surge along the Gulf of Mexico and U.S. east coast. Journal of Ocean University of China, 16(1): 1-7. (  0) 0) |
Yin, X., Wang, Q., Lv, X., Xing, L., Li, Z., Shan, P., et al., 2018. Research on the numerical simulations of marine hydrodynamic and pollutant diffusion in Bohai Bay. Desalination & Water Treatment, 122: 277-283. (  0) 0) |
Zhang, W., Leung, Y., and Fraedrich, K., 2015. Different El Niño types and intense typhoons in the western North Pacific. Climate Dynamics, 44(11-12): 2965-2977. (  0) 0) |
Zhang, Y., Li, G., and Guo, T., 2019. Spatiotemporal patterns and evolution of storm surge threats along the southeastern coastline of China. Atmosphere, 10(2): 61. (  0) 0) |
Zhao, B., Qu, X., Zhu, X., and Ye, J., 2021. Ocean surface responses to super typhoon in coastal zone based on biogeochemical buoys data: A case study of 'Lekima'. Continental Shelf Research, 227: 104505. (  0) 0) |
 2025, Vol. 24
2025, Vol. 24


