2) Shandong Provincial Key Laboratory of Marine Environment and Geological Engineering, Ocean University of China, Qingdao 266100, China;
3) Laboratory for Marine Geology, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266061, China;
4) College of Marine Geosciences, Ocean University of China, Key Laboratory of Submarine Geosciences and Prospecting, Qingdao 266100, China
Piezocone penetration test (CPTu) is the most commonly used in-situ testing method in marine site investigation. In practice, the standard penetration rate of CPTu is (20 ± 5) mm s−1. At this penetration rate, sandy soils exhibit fully drained behavior and cohesive soils exhibit fully undrained behavior. The effective internal friction angle of sandy soils and the undrained shear strength of clayey soils can be accurately measured by CPTu, but for soils of medium grain size with properties between clay and sand, the soil strength is often measured by regional empirical methods.
The field penetration tests conducted in multiple regions have shown that the penetration rate significantly affects the results of CPTu on intermediate grain size soils (Chung et al., 2006; Salgado et al., 2010; Poulsen et al., 2013; Krage et al., 2014). The effect of penetration rates on CPTu results is manifested in two aspects: 1) the penetration resistance decreases with the increase of penetration rate due to drainage behavior; 2) the penetration resistance increases with the increase of penetration rate due to the viscous effect. Although negligible in both sand and clay, the effect of penetration rate is significant in intermediate grain size soils. The confidence level of geotechnical parameter estimation can be very low under the partial drainage conditions (DeJong and Randolph, 2012; DeJong et al., 2012). Disregarding the effect of penetration rates may distort the inversion results (Suzuki and Lehane, 2015). These problems all call for the study on the effect of penetration rates on CPTu under partial drainage conditions.
Quantitative studies have been carried out by centrifuge tests and calibration tank tests to reveal the influencing factors and the mechanism of the effect of penetration rates on CPTu in intermediate soils. Centrifuge tests have shown that penetration rates are affected by partial drainage behaviors and cohesive effects to different degrees in different soils (Finnie and Randolph, 1994; Lunne and Andersen, 2007; Lehane et al., 2009). As for the dilatancy silt, it is the cohesive effect that causes more significant impact (Silva et al., 2006).
To investigate the effect of penetration rates through numerical simulations, Silva (2005) has modeled the cylindrical cavity expansion with variable penetration rates by CAMFE FE code and found that the test results did not coincide with those of the centrifuge test performed by Randolph and Hope (2004). Jaeger (2012) has analyzed the cylindrical cavity expansion by FLAC3D software with the finite difference method and the results are in agreement with those obtained by Sliva (2005). The one-dimensional axisymmetric geometry adopted for modeling the cylindrical cavity expansion may not be suitable for simulating the actual vertical and horizontal drainage around the cone tip. Yi et al. (2012) and Mahmoodzadeh et al. (2014) have used the large deformation finite element analysis method and effective stress analysis to study partial drainage effect on normally consolidated clay. The results were in good agreement with those obtained by the centrifuge test conducted by Mahmoodzadeh and Randolph (2014). Two-phase material point method, characterized by a contact algorithm, was used to simulate CPTu test under partial drainage conditions, in which soil behavior is described with the MCC model (Ceccato et al., 2016). This method also takes into account the large deformation of soil and the dissipation of pore pressure during penetration, and the results agree well with experimental data. Monforte et al. (2018) applied the particle finite element method, which is capable of tackling large deformation problems, to the parametric analysis of the CPTU test in the material described in a Cam-clay hyperelastic model. Spherical cavity expansion has also been modeled in numerous studies with the finite element analysis software PLAIXS (Xu and Lehane, 2008; Lehane et al., 2009; Tolooiyan and Gavin, 2011). It has been found that after reconsolidation, the dissipation of excess pore pressure and the increase in effective radial stresses start earlier in the spherical scenario than in the cylindrical scenario (Mo et al., 2020). The comparison between the calculated ultimate cavity expansion pressure and the measured value confirmed that spherical cavity expansion analysis was more suitable for understanding the effect of local consolidation after drainage during CPTu (Yu, 2000; Cao et al., 2001). Coupled with the consolidation analysis, spherical cavity expansion analysis could be performed to investigate the effect of variable penetration rates on CPTu (Suzuki, 2010).
Given that the permeability and mechanical properties of the widely distributed silt layers in the Yellow River Delta are significantly different from that of typical clay and sand layers, there is still a lack of theoretical support for the penetration rate effect of the Yellow River Delta silt. The understanding of the effect of penetration rates on CPTu of silt soils has not been theoretically supported. At present, the CPTu on sediments in the Yellow River Delta region is mainly based on regional empirical coefficients (Guo and Prakash, 1999; Chu, 2017; Dong et al., 2018). A large amount of sediment accumulates at the Yellow River Delta region with over 90% of silt (Feng et al., 2002). Because of spatially non-uniform soil strength (Zhou et al., 2006), submarine geohazards such as landslides (Zhao et al., 2020) and seabed liquefaction (Yang et al., 2019; Song et al., 2020) frequently occur, causing numerous accidents including the suspension or fracture of submarine pipelines and the tilt of offshore platforms.
To study the effect of penetration rates on CPTu in the typical Yellow River Delta silt under partial drainage conditions and provide a reliable evaluation method for field CPTu tests, spherical cavity expansion was modeled with PLAXIS to simulate the penetration process of CPTu according to the spherical cavity expansion theory. Indoor 1 g model tests with different penetration rates were performed for comparison with numerical simulation results. The evaluation method of CPTu test results was proposed and the penetration and consolidation properties of silt under partial drainage conditions were obtained in this paper, which provided some valuable support for marine engineering construction in the Yellow River Delta.
2 Numerical Analysis of the Piezocone Penetration Resistance Under Variable Penetration Rates 2.1 Design and Numerical CalculationBased on the spherical cavity expansion theory, the piezocone penetration modeling is simplified to a spherical cavity expansion process. The generation and dissipation characteristics of excess water pressure due to spherical cavity expansion can be predicted by using coupled consolidation calculations in PLAXIS software, which is designed to discuss the factors affecting the cone tip resistance under different drainage conditions. The numerical simulations in this paper are based on a nonlinear elastic-plastic hardening intrinsic model with spherical cavity expansion modeling. The method is similar to those proposed by Xu (2007), Xu and Lehane (2008), and Suzuki (2015). The CPTu cone tip resistance under different drainage conditions is measured.
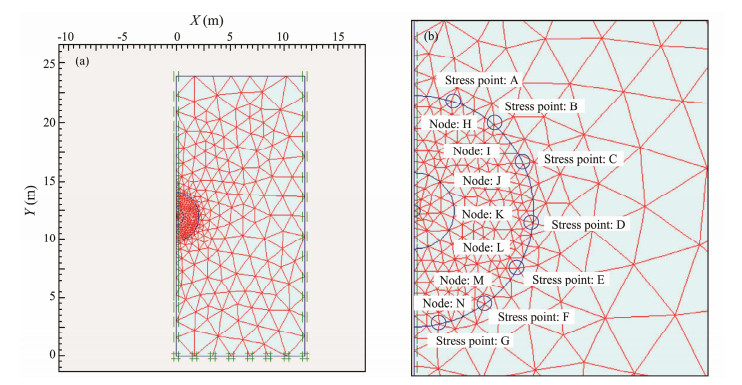
An axisymmetric soil domain (about 1200 elements) is created in the X-Y plane as shown in Fig.1 (effect of mesh coarseness has been shown to be not sensitive to the results at this sufficiently fine mesh). A spherical cavity of 0.1 m in radius (a0) without lining or interface is set at a depth of 12 m. Spherical cavities of 0.7 m and 2.1 m in radius are also set to partition the axisymmetric soil domain into four class groups. The boundary conditions are completely fixed at the bottom, completely free at the top, and partially free at the left and right boundaries in the vertical direction only. Material properties are imposed on the cavity and the surrounding soil body, with a linear elastic model for the cavity and a hardening soil model (HS model) for the surrounding soil body. A triangular cell mesh is generated and further refined near the cavity where large strains are expected to occur.
|
Fig. 1 Grid generation diagram. (a), gridding model; (b), distribution of nodes and stress points around the cavity. |
The water level line is set at the upper boundary of the soil model and the initial effective stress is generated according to the K0 = 1− sinφ' consolidation procedure. According to the axisymmetric unit, seven stress points (A – G) and seven nodes (H – N) are selected on the cavity wall and the nodes close to the cavity wall, respectively. Stress expansion curves and pore pressure curves are generated based on the average values of radial displacements at the seven nodes and the average values of radial stresses and excess pore water pressure at the seven stress points.
At the first stage, the initial stresses are calculated with the guarantee that the ground stresses are balanced. At the subsequent stages, the volume strain in the 'Calculation' program (i.e., 10% increase in each stage) is applied to the spherical cavity, resulting in gradual expansion of the spherical cavity. This large deformation problem is solved in PLAXIS by using the update grid option. The cavity must be expanded to at least twice in radius than the initial cavity. Each calculation stage (always starting from the initial stress condition) defines a different consolidation time, representing a different rate of cavity expansion.
The main model adopted in this paper is the HS model. The relevant input parameters are shown in Table 1. In contrast to the Mohr-Coulomb model, the HS model has advanced features to account for strain-stress dependent Young's modulus. Full description of the HS model is provided by PLAXIS reference manual (Brinkgreve et al., 2012).
|
|
Table 1 Input parameters for HS model |
In PLAXIS coupled consolidation analysis, the generation and dissipation of excess static pore pressure during cavity expansion can be simulated for a given consolidation time. Thus, the equation for calculating the radial expansion velocity of the cavity is:
| $ {v_{{\text{r}}\_{\text{CE}}}} = \frac{{\Delta {r_{{\text{CE}}}}}}{{\Delta {t_{{\text{CE}}}}}}, $ | (1) |
where ∆rCE is the radial displacement of the cavity wall; ∆tCE is the expansion time corresponding to the displacement. In this study, the cavity expanding pressure (σ1) at a/a0 = 2 is used as an approximation of the limit pressure. The relationship between the limit pressure (plimit) and the steady state cone end resistance (qc) is expressed as follows (Silva et al., 2006; Suzuki, 2015):
| $ {q_{\text{c}}} = {p_{{\text{limit}}}} + \sqrt 3 \left({{p_{{\text{limit}}}} - u} \right)\tan \delta, $ | (2) |
where the interface friction angle δ was assumed as same as the constant volume friction angle φcv of the soils.
The cavity expansion at the velocity of 0.0152, 0.152, 1.52, 15.2, 152 and 1520 mm s−1 (over six orders of magnitude) were analyzed by changing the given consolidation time in each phase. A total of 27 cases were analyzed in this paper, which were divided into three groups. The basic parameters used in all analytical cases are listed in Table 2, and the variables of all designed cases are summarized in Table 3.
|
|
Table 2 Basic parameters regularly used for all analytical cases |
|
|
Table 3 Variables of all cases used in analysis program |
The total radial stress, excess water pressure and radial displacement of the cavity wall were taken as the average values of all the 7 stress points and 7 nodes. The cavity expansion pore pressure curve and stress curve were obtained to demonstrate the cavity expansion process. The typical results of these two curves are shown in Fig.2.
|
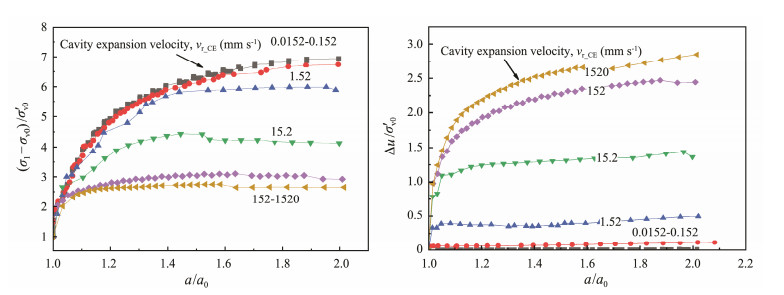
Fig. 2 A typical result on: (a), normalized cavity expanding pressure; (b), normalized excess pore pressures generated at the site closed to the cavity wall (HS08). |
As a result of varying the cavity expansion velocity from 0.0152 to 1520 mm s−1, the normalized cavity expanding pressures and the normalized excess pore pressures can clearly indicate whether the soil is drained or not. The ∆u/σ'v0 values decrease rapidly with the decrease of vr_CE from 1520 mm s−1 to 152 mm s−1, then decrease more dramatically when vr_CE furtherly reduces to 152 mm s−1 and 1.52 mm s−1. Significant increases in the (σ1 − σv0)/σ'v0 values also occurred at vr_CE of 152 – 1.52 mm s−1, indicating that the cavity expansions were likely to be under the partially drained condition in these cases. Fully drained conditions were also confirmed at vr_CE below 0.0152 mm s−1.
2.3 Effect of Key Parameters 2.3.1 Effect of E50 and φ'Studies investigating the effect of penetration rates under the partially drained condition often use the normalized velocity (V) to unify the data (Finnie and Randolph, 1994), which is defined as
| $ {V_{\text{v}}} = \frac{{vd}}{{{c_{\text{v}}}}}, $ | (3) |
where v is the penetration rate, d is the piezocone diameter, and cv is the vertical consolidation factor.
Silva et al. (2006) and Lehane et al. (2009) suggested to use a horizontal coefficient of consolidation (ch), instead of cv, for 1-D consolidation analysis on a laboratory sample. For the HS model, ch may be calculated as:
| $ {c_{\text{h}}} = \frac{{{k_{{\text{h}}0}}{E_{50}}}}{{{\gamma _{\text{w}}}}}, $ | (4) |
where E50 was secant stiffness at the initial stress condition and γw is the unit weight of the water, then the normalized velocity (Vh_CE) can be defined as (Suzuki, 2015):
| $ {V_{{\text{h}}\_{\text{CE}}}} = \frac{{{v_{{\text{r}}\_{\text{CE}}}}{d_{{\text{CE}}}}{\gamma _{\text{w}}}}}{{{k_{{\text{h}}0}}{E_{50}}}}, $ | (5) |
where dCE are taken as the final cavity diameter (two times of the final cavity radius); kh0 is assumed to be constant during expansion.
Assuming that the cavity expansion limit pressure is equal to the total radial stress of the cavity, the theoretical cone tip resistance value is calculated according to Eq. (2) and normalized as follows:
| $ Q = \frac{{{q_{\text{c}}} - {\sigma _{{\text{v}}0}}}}{{{{\sigma '}_{{\text{v}}0}}}}. $ | (6) |
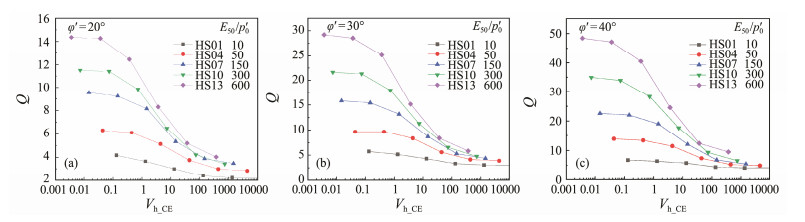
Whether the drainage occurred or not can be clearly observed by changing the normalized velocity. According to Fig.3, the normalized penetration resistance values decrease significantly when Vh_CE is between 0.1 mm s−1 and 100 mm s−1, a rate interval in which partially drained conditions are usually considered to be achieved. The normalized velocity needs to change by at least three orders of magnitude from fully drained to fully undrained conditions.
|
Fig. 3 Variations of the normalized cone resistance at different representative penetration rates for soils with different stiffness and constant friction angle. (a), φ' = 20˚; (b), φ' = 30˚; (c), φ' = 40˚. |
Also in Fig.3, the significant effect of the strength and internal friction angle of the soil on the cone tip resistance is shown. Taking Fig.3b as an example, there is a good positive correlation between the stiffness and the normalized cone tip resistance in the soil body with a given friction angle. And for the soil body with a given stiffness ratio, the larger the friction angle is, the larger the resistance of the CPTu is. The results are in agreement with those of coupled-consolidation finite-element analyses of Yi et al. (2012).
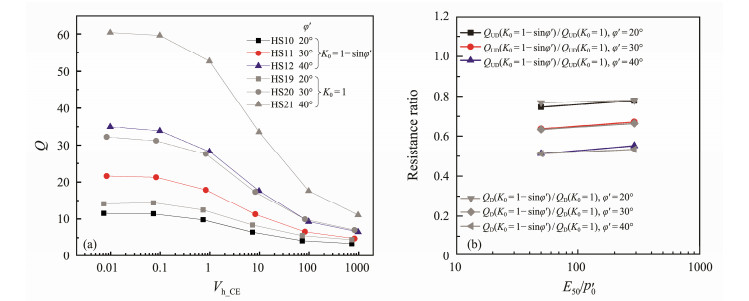
2.3.2 Effect of K0In Fig.4a, it can be found that K0 severely affects the cone tip resistance at any normalized velocity. Soils in isotropic conditions from HS19 to HS21 exhibit larger Q values at any normalized velocity compared to soils from HS10 to HS12 when K0 = 1− sinφ'. Especially in the case of equal vertical effective stresses, the latter would produce greater horizontal effective stresses around the cavities. According to the equations defining the parameters of the HS model, the higher initial values of E50 and Eur need to be produced by the larger horizontal effective stresses. Therefore, for the expansion of cavity, to reach a predetermined radial displacement requires a greater pressure. According to Fig.4b, for a given stiffness and friction angle, the penetration resistance ratio is essentially the same under the drained and undrained conditions, and the ratio is independent of the stiffness modulus.
|
Fig. 4 Effect of in situ lateral earth pressure coefficient K0. (a), Q vs. velocity diagram; (b), resistance ratios at different φ'. |
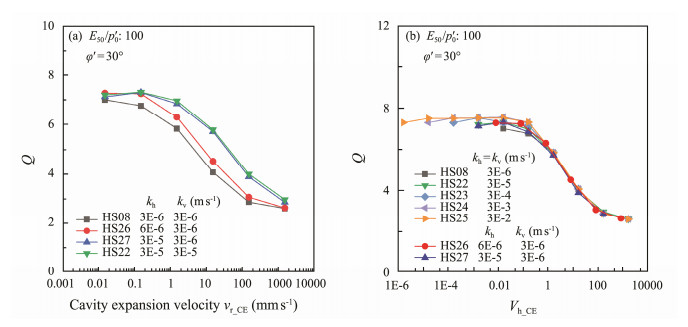
The effect of anisotropic permeability is shown in Fig.5a. The curve of case HS26 shifts to the right when the horizontal permeability (kh) is doubled (kv is maintained at 3× 10−6 m s−1) compared to the curve of case HS08. This implies that the drainage of soil is faster than that of the original (HS08) case. When kh increases by an order of magnitude (kv remains unchanged), the curve shifted further to the right, but does not overlap with the HS22 case (kh and kv both increase by one order of magnitude). This result confirms that both horizontal and vertical permeability have an effect on the drainage characteristics during cavity expansion, but the effect of kh is greater than kv. This is due to the fact that the water flow is mainly horizontal, and it also indicates that kh may be a better normalized parameter than kv in defining general drainage conditions for different soil anisotropic permeability. In Fig.5b, except HS26 and HS27, we add five curves obtained at five orders of isotropic permeability to verify the reasonableness of using kh for velocity normalization. The Q-Vh_CE curves approximately coincide in a single curve, which indicates that the effect of permeability is being well taken into account.
|
Fig. 5 (a), Effect of anisotropic permeability; (b), the cone tip resistance vs. normalized velocity Vh_CE. |
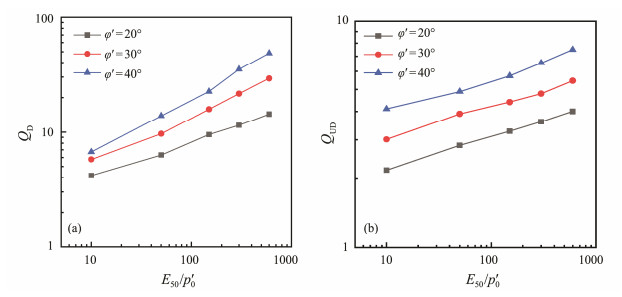
The normalized cone tip resistance values (QD, QUD) with and without drainage are extracted from Group I. It is evident that as the soil stiffness and friction angle change, the calculated (QD, QUD) values also change, showing good linear relationships between logQD, logQUD, and logE50 /p'0, as shown in Figs.6a and 6b.
|
Fig. 6 The normalized cone resistance variation as the function of friction angle and stiffness on log-log scale. (a), drained conditions; (b), undrained conditions (K0 = 1− sinφ'). |
Therefore, based on the HS model cavity expansion analysis, QD, QUD can be reasonably estimated by using the fitting method proposed by Suzuki (2015).
| $ {Q_{\text{D}}} = \frac{{{q_{{\text{cD}}}} - {\sigma _{{\text{v}}0}}}}{{{{\sigma '}_{{\text{v}}0}}}} = 5.974{\left({\sin \varphi '} \right)^{1.428}}{\left({\frac{{{E_{50}}}}{{{{p'}_0}}}} \right)^{0.398}}, {\text{ }}{R^2} = 0.974, $ | (7) |
| $ {Q_{{\text{UD}}}} = \frac{{{q_{{\text{cUD}}}} - {\sigma _{{\text{v}}0}}}}{{{{\sigma '}_{{\text{v}}0}}}} = 4.248{\left({\sin \varphi '} \right)^{0.926}}{\left({\frac{{{E_{50}}}}{{{{p'}_0}}}} \right)^{0.144}}, {\text{ }}{R^2} = 0.99, $ | (8) |
where qcD and qcUD are the cone tip resistances under drained/undrained conditions estimated from Eq. (2). The equation is based on Group I calculations, where the friction angle ranges from 20˚ to 40˚, the stiffness ratio ranges from 20 to 480, the over consolidation ratio OCR is 1, the static earth pressure coefficient K0 = 1− sinφ', and the shear-induced volume expansion or compression is not considered.
2.5 Prediction of Partially Drained ResistanceA hyperbolic function relating normalized cone resistance (Q) and the normalized velocity (Vh_CE) can be expressed as (House et al., 2001):
| $ Q = \frac{{q{\text{c}} - \sigma {\text{v}}0}}{{\sigma '{\text{v}}0}} = {Q_{{\text{UD}}}} + \frac{{{Q_{\text{D}}} - {Q_{{\text{UD}}}}}}{{1 + a{{({V_{{\text{h_CE}}}})}^{0.80}}}}, $ | (9) |
where QD and QUD can be determined from Eqs. (7) and (8), a is a constant.
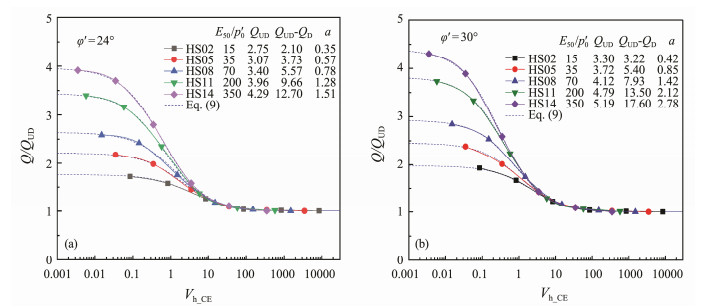
The effects of E50 /p'0 on Q/QUD ratios in the partially drainage range are well explained by Eq. (9) (for the soils with φ' = 24˚ and 30˚). As seen in Fig.7, the values of fitting parameter a also tend to increase with E50 /p'0. It can be seen that the hyperbolic function can effectively predict the cone resistances. In addition, it can be seen that the soil stiffness has a significant effect on the parameters in the Fig.7.
|
Fig. 7 Comparison of rate effect data with the hyperbolic curves. (a), φ' = 24˚; (b), φ' = 30˚. |
To obtain the variable penetration rate, a penetration rack unit was designed with indoor segmented penetration rate control equipment, as shown in Fig.8. With a diameter of 10 mm, a cone top angle of 60˚, a cone tip cross-sectional area of 78.54 mm2 and a friction sleeve area of 1162.39 mm2, the miniature piezocone is mounted on a servo motor driver, which can penetrate through the predrilled hole in the top plate into the soil samples at the controlled rate of 0.005 – 20 mm s−1. The mini-CPTu can measure the cone tip resistance qc, the sleeve friction resistance fs and the cone shoulder pore water pressure u2.

|
Fig. 8 1 g model test equipment. |
Two set of samples from Yellow River Delta silt and Malaysia kaolin were prepared. Basic geotechnical tests, one-dimensional consolidation tests and triaxial shear tests were performed on the two soil samples. The physical and mechanical properties, consolidation properties and strength of the remodeled samples were measured.
Table 4 summarizes the physical properties of Malaysia kaolin and Yellow River Delta silt, and Table 5 summarizes the consolidation coefficient cv at effective stress levels in the range of 25 to 150 kPa.
|
|
Table 4 Physical property indexes of Yellow River Delta silt and Malaysia kaolin |
|
|
Table 5 Test results of consolidation coefficient cv for Yellow River Delta silt and Malaysia kaolin |
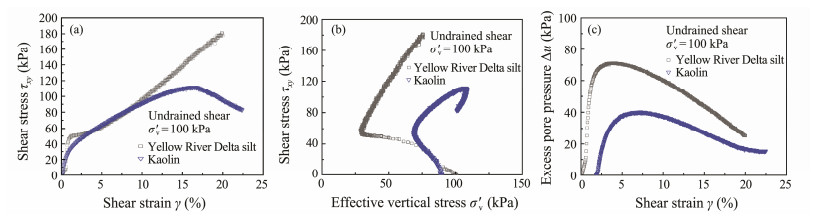
The results of the undrained test at a consolidation stress of 100 kPa are shown in Fig.9. The shear properties are strongly influenced by the clay fraction. Based on the undrained triaxial shear test, the range of apparent peak friction angle of the Yellow River Delta silt φ'p was estimated to be 28˚ – 32˚, with a mean value of 30˚.
|
Fig. 9 Undrained shear test results of Yellow River Delta silt and Malaysia kaolin. (a), τxy vs. γ; (b), τxy vs. σ'v; (c), ∆u vs. γ. |
During sample preparation, the water content was adjusted by adding water to twice the liquid limit. The samples were stirred under negative pressure for 4 h with a vacuum stirring device before slowly poured into the sample preparation drum. Then the samples were compressed by a consolidation system which had an inner diameter of 60.0 cm, a wall thickness of 10.0 mm, and a height of 80.0 cm. Geofabrics was used to separate the top and bottom plates from the samples. A drainage conduit with a valve was installed on the bottom of the drum and round holes were cut on the top plate so that water can be drained from both ends. A layer of fine sand approximately 30 mm thick was applied on top of the Malaysia kaolin clay to accelerate the consolidation. The consolidation system was constructed with a standard cylinder, a threaded rod and a counterforce frame. Pressure was applied evenly to the samples by an air pump. After consolidation, the sample container was placed on the test rig under a loading pressure of 50 kPa for over 24 h to maintain normal consolidation condition of the samples. The whole preparation process is shown in Fig.10.
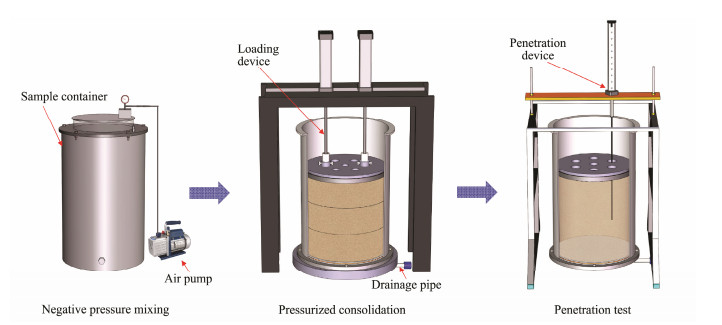
|
Fig. 10 Soil sample preparation process. |
Due to conducted in a relatively small vessel, the boundary effect of the penetration tests cannot be neglected. The finite element numerical simulation on the spherical cavity expansion was performed and the possible boundary effects of this test was analyzed based on the parameters of Yellow River Delta silt. The detailed numerical modeling procedure has been presented in Section 2.
The radius r of the miniature piezocone is 5 mm, and the minimum distance D from the probe center to the inner wall of the cavity is about 100 mm. To simulate the critical case where D/r = 20, the soil area radius R is set to 4 m in the axisymmetric numerical analysis. The cavity radius was expanded from a0 = 0.1 m to af = 0.2 m (i.e., R/af = 20).
As shown in Fig.11, the excess pore pressures (∆u) and the cavity limit pressures (σ1) close to the cavity wall are little affected by R/af at different rates of cavity expansion. Fig.11a shows the radial pore water pressure distribution at a depth of 12 m after undrained cavity expansion, indicating almost no boundary effect on the cavity expansion pressure when R/af = 60. The predicted values when R/af = 20 is approximately 7% higher than that when R/af = 60 as radial water flow was restricted by the lateral boundary. As shown in Fig.11b, at a certain range of cavity expansion velocities, the cavity expansion pressure on the cavity wall is slightly affected by the distance away from the boundary. When R/af = 20, the cavity expansion pressure is 5% higher than that when R/af = 60, so 20 times of the piezocone radius was used for R in the 1 g model test.
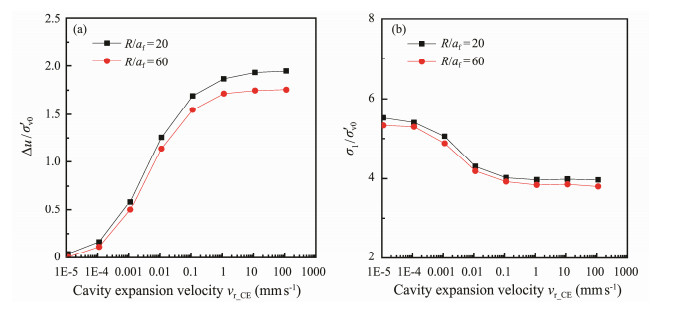
|
Fig. 11 Boundary effects at different cavity expansion velocities on (a) excess pore pressure at sites close to the cavity wall and (b) cavity limit pressure on the cavity wall. |
Thirteen penetration tests distributed as shown in Fig.12 were performed on each sample. The interval between two tests was 24 h to minimize the influence of excess pore pressure generated during previous penetration. Considering the boundary conditions, the penetration holes are at least 100 mm (20 times the piezocone radius) away from the cylinder wall or each other. To ensure the accuracy of the results and the homogeneity of the samples, four sets of repeatability tests were carried out, and the results showed that the test was repeatable and the samples were homogeneous.

|
Fig. 12 The distribution of penetration test holes. |
The penetration tests were conducted at a constant penetration rate at the start and once a predetermined penetration depth was reached, the penetration rate began to change from 0.005 to 20 mm s−1 (the piezocone vibrated at 0.005 m s−1). Adopting a relatively faster penetration rate at the shallower depths was to check the consistency of CPTu measurements between each penetration test, thus ensure that the interaction between the different penetrations was minimal. A corrected total cone resistance (qt) was calculated by using the following relationship, which has involved the unequal pore pressure effect (Lunne et al., 1997b):
| $ {q_{\text{t}}} = {q_{\text{c}}} + {u_2}(1 - \alpha), $ | (10) |
where qc is the measured cone resistance, u2 is the pore pressure measured at the cone shoulder and α is the unequal area ratio (0.8 for the CPTu).
Fig.13a shows the results of a typical penetration test on a Malaysia kaolin soil sample. The penetration depth of the miniature piezocone is about 300 mm, and the penetration rate v starts to change at the depth of 150 mm. The measurements reached stable after a period of time following the change of penetration rate. At the penetration rate v of 1 mm s−1, the corrected cone tip resistance qt of the Malaysia kaolin sample was relatively constant at 75 ± 5 kPa. The qt when v = 0.005 mm s−1 exceeds that when v = 1 mm s−1 (approx. 60 kPa) and reaches a constant value of approximately 110 kPa. When v = 0.005 mm s−1, pore water pressure u2 of the Malaysia kaolin sample at the target depth is approximately 10 kPa.
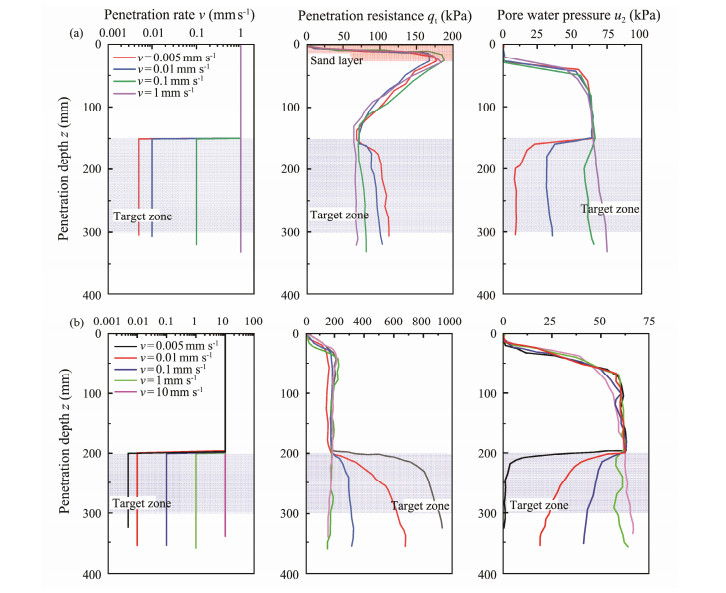
|
Fig. 13 Typical penetration profiles of CPTu in Malaysia kaolin sample (a) and Yellow River Delta silt sample (b). |
Fig.13b shows the typical penetration test results for the Yellow River Delta silt samples. When v = 10 mm s−1, qt was stable at 150 kPa. Pore water pressure u2 at a depth of 50 mm was 60 kPa. The qt and u2 measured when v = 1 mm s−1 were similar to those measured when v = 10 mm s−1. When v = 0.01 and 0.005 mm s−1, qt and u2 are significantly different from those at higher penetration rates.
Fig.14 shows the comparison of penetration rate effect on CPTu results between the two soil samples in terms of normalized cone tip resistance (Q = qnet /σ'v0, the net cone resistance qnet was calculated as: qnet = qt − σv0, where σv0 is the total vertical stress) and normalized pore pressure ratios (∆u/σ'v0, where u = u2− u0, u0 is the hydrostatic pore pressure about 1 to 2 kPa and σ'v0 is vertical effective stress). Based on Fig.14a, Q values are rather different between the two soil samples when normalized penetration rate Vv < 10.
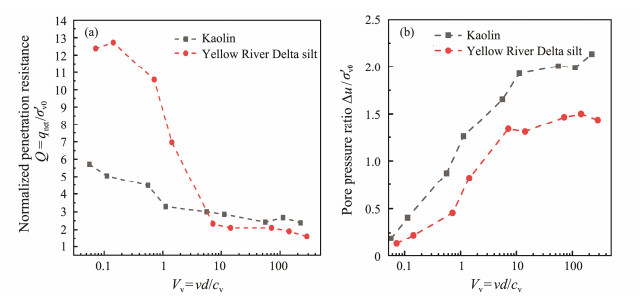
|
Fig. 14 Effects of penetration rate on piezocone parameters of Yellow River Delta silt and Malaysia kaolin samples. (a), normalized penetration resistance at different penetration rates; (b), pore pressure ratio at different penetration rates. |
According to Fig.14, since the value Q at Vv of 1 is similar to those when Vv > 10 for the Malaysia kaolin sample, the transition from undrained to partially drained conditions based on the change in normalized cone tip resistance is not fully consistent with that based on the change in pore pressure u2 at the cone shoulder, which is referred to as the 'offset effect' by Kim (2005).
4 Discussion 4.1 Validation of 1 g Model TestsResults from 1 g model tests at the different penetration rates designed in this paper are compared with the experimental results obtained by centrifuges and calibration tanks.
Fig.15 shows the result comparison in Malaysia kaolin between 1 g model test and two centrifuge tests performed by Randolph and Hope (2004) at 100 g and Schneider et al. (2007) at 160 g. The drained resistance in the 1 g test is a slightly lower than those in the centrifuge test, mainly because the maximum stress generated in the centrifuge test was approximately twice than in the 1 g test. As shown in Fig.15b, the Malaysia kaolin undergoes a transition from undrained to partially drained at the normalized penetration rate Vv of 100 and from partially drained to fully drained at the normalized penetration rate Vv of 0.1.
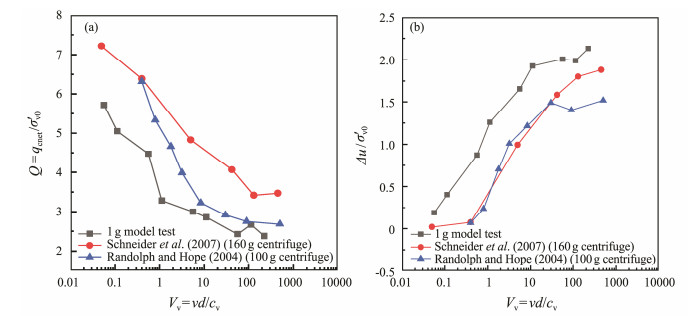
|
Fig. 15 Comparisons of penetration test results in Malaysia kaolin with those of previous works. (a), Q-Vv; (b), ∆u/σ'v0-Vv. |
Fig.16 shows the comparison between the 1 g model test in the Yellow River Delta silt and the experimental studies of Jaeger et al. (2010) and Kim et al. (2008) on the mixture of silt with 25% kaolin. As the normalized penetration rate reduces by 2 to 3 orders of magnitude, all normalized penetration resistances Q increase significantly and the corresponding pore pressure ratios decrease significantly. The normalized penetration rate Vv values to make the soil under undrained and partially drained conditions were in the range of 10 – 30, and the normalized penetration rate Vv values to make the soil change from partially drained to fully drained conditions were in the range of 0.03 – 0.06. Similar transitions of drainage conditions can be observed in two different test methods, 1 g test and centrifuge test, based on the differences in measured drained resistance and undrained resistance, which result from the differences in density and preparation techniques of soil samples.
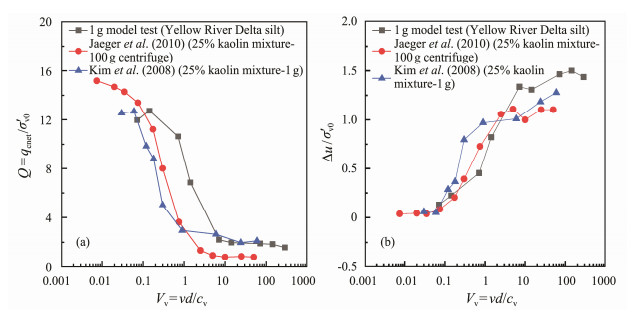
|
Fig. 16 Comparisons of penetration test results in Yellow River Delta silt with those of previous works. (a), Q-Vv; (b), ∆u/ σ'v0-Vv. |
The results from the 1 g test on Malaysia kaolin in this paper were compared with that of the PLAXIS cavity expansion calculations. The normalized penetration rate Vv was used in the 1g model tests. The horizontal consolidation efficiency was considered equal to the vertical one due to the use of remodeled soils with one-dimensional consolidation, which are assumed to have isotropic permeability (Wang et al., 2015). Therefore, Vv is able to be compared with the normalized penetration rate Vh in the numerical simulation. In the numerical simulation for a cone with a vertex angle of 60˚, the cone penetration velocity (vcone) in the vertical direction is half of vr_CE. Due to the assumption that the volume of the soil pushed out during the cavity expansion is equivalent to the volume of the cone tip, the diameter of the cavity (dCE) can be considered as approximately 0.8 times the diameter of the cone penetrometer (dcone). Then the normalized penetration rate Vh, which is linked to the CPTu based on Eq. (5), can be calculated as:
| $ {V_{\text{h}}} = \frac{{{v_{{\text{cone}}}}{d_{{\text{cone}}}}{\gamma _{\text{w}}}}}{{{k_{{\text{h}}0}}{E_{50}}}} . $ | (10) |
The Malaysia kaolin samples have the friction angle of 24˚ and stiffness modulus (E50/p'0) of about 42 to 62, according to the measurement in triaxial compression tests by Stewart (1990).
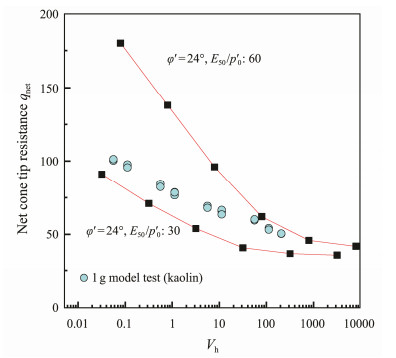
|
Fig. 17 Comparison of net cone tip resistance obtained by PLAXIS analysis and 1 g test in Malaysia kaolin. |
The PLAXIS cavity expansion analysis provides the good simulation to the trend of net cone tip resistance with the penetration rate and reflects the transition in drainage conditions. Moreover, the stiffness modulus has a more significant effect on the trend of CPTu test results with the penetration rates.
The results of PLAXIS cavity expansion calculation are compared with the results of 1 g test for the Yellow River Delta silt. Base on the triaxial tests, the Yellow River Delta silt has a friction angle of 30˚. The compression index and recompression index of Yellow River Delta silt are about one fifth and one sixth of Malaysia kaolin, respectively. These relative magnitudes suggest a modulus ratio (E50/p'0) in the range of 200 to 240.
The normalized penetration rate for the transition from drained to undrained conditions determined by the PLAXIS cavity expansion analysis (0.12 – 120) is slightly larger than the 1 g model test results (0.06 – 30), which may be due to the overestimated shear strength and cone resistance at fast (undrained) expansions caused by Dilation cut-off option in HS model. Also the model (ψ = 0) does not provide realistic predictions for highly compacted soils.

|
Fig. 18 Comparison of net cone tip resistance obtained by PLAXIS analysis and from 1 g test in Yellow River Delta silt. |
In the engineering survey of the Yellow River Delta region, the partial drainage of silt layer is a key factor in affecting the CPTu test results. The curves of soil properties under the partial drainage conditions can provide some valuable reference for CPTu data interpretation in the Yellow River Delta. In this paper, the range of penetration rate to make the silty soils partial drainage in the Yellow River Delta is determined by the numerical simulation and the 1 g model test. The reference drainage curve is given and the reference resistance under the normalized penetration rate (zero dilation and zero viscous effects) is predicted. The main conclusions are summarized as follows:
1) The parameters measured during CPTu penetration are closely related to the drainage degree caused by the change of penetration rates. When the normalized penetration rate decreases by 2 – 3 orders of magnitude, the normalized penetration resistance Q increases significantly and the pore pressure ratio decreases greatly. The results of 1 g model test show that the normalized penetration rate Vv to make the Yellow River Delta silt under the undrained and partially drained conditions is between 10 and 30, and the values of Vv to make the soil change from partially drained to fully drained conditions is from 0.03 to 0.06.
2) Numerical simulation of spherical cavity expansion coupled with consolidation analysis by the HS soil model showed that the normalized penetration rate Vh in which can trigger the partially drainage of the Yellow River Delta silt changed at least three orders of magnitude (approximately 0.12 – 120). Both stiffness and friction angle have significant effects on the QUD and QD for normally consolidated soils assumed to expand freely, and the influence of stiffness is relatively greater.
3) Numerical simulation provides the reference resistance corresponding to zero expansion and zero viscous at any normalized velocity, which makes the data obtained on the actual silt soils in Yellow River Delta can be interpreted in terms of penetration rates.
AcknowledgementsThe study is supported by the National Natural Science Foundation of China (Nos. U1806230, U2006213), and the Fundamental Research Funds for the Central Universities (No. 201962011).
Brinkgreve, R. B. J., Engin, E., and Swolfs, W. M., 2012. PLAXIS 2D 2012. PLAXIS B. V., The Netherlands, 14pp.
(  0) 0) |
Cao, L. F., Teh, C., and Chang, M.. 2001. Undrained cavity expansion in modified Cam clay Ⅰ: Theoretical analysis. Géotechnique, 51(4): 323-334. DOI:10.1680/geot.2001.51.4.323 (  0) 0) |
Ceccato, F., Beuth, L., and Simonini, P.. 2016. Analysis of piezocone penetration under different drainage conditions with the two-phase material point method. Journal of Geotechnical and Geoenvironmental Engineering, 142(12): 4016066. DOI:10.1061/(ASCE)GT.1943-5606.0001550 (  0) 0) |
Chu, L. P., Sun, Y. F., and Song, Y. P.. 2017. Application of seabed cone penetration test in research on the seafloor geotechnical engineering characteristics in the Yellow River Estuary. Coastal Engineering, 36(1): 23-32 (in Chinese with English abstract). (  0) 0) |
Chung, S. F., Randolph, M. F., and Schneider, J. A.. 2006. Effect of penetration rate on penetrometer resistance in clay. Journal of Geotechnical and Geoenvironmental Engineering, 132(9): 1188-1196. DOI:10.1061/(ASCE)1090-0241(2006)132:9(1188) (  0) 0) |
DeJong, J. T., and Randolph, M. F.. 2012. Influence of partial consolidation during cone penetration on estimated soil behavior type and pore pressure dissipation measurements. Journal of Geotechnical and Geoenvironmental Engineering, 138(7): 1-13. (  0) 0) |
DeJong, J. T., Jaeger, R. A., Boulanger, R. W., Randolph, M. F., and Wähl, D. A. J., 2012. Variable penetration rate cone penetration testing for characterizing intermediate soils. The Proceedings of 4th International Conference on Geotechnical and Geophysical Site Characterization (ISC4). Porto de Galinhas, Pernambuco, 25-42.
(  0) 0) |
Dong, L., Yan, W. J., Xia, K., Li, S. H., and Liu, K.. 2018. In-situ tests and liquefaction potential evaluation for saturated loess sites. Technology for Earthquake Disaster Prevention, 13(4): 219-227 (in Chinese with English abstract). (  0) 0) |
Feng, X. L., Ye, Y. C., Ma, Y. X., and Lin, L.. 2002. Silt pore pressure response and dynamic strength under dynamic loading. Journal of Ocean University of Qingdao, 32(3): 426-433 (in Chinese with English abstract). (  0) 0) |
Finnie, I. M. S., and Randolph, M. F., 1994. Punch-through and liquefaction induced failure of shallow foundations on calcareous sediments. Proceedings of 7th International Conference on the Behaviour of Offshore Structures. Boston, 217-230.
(  0) 0) |
Guo, T., and Prakash, S.. 1999. Liquefaction of silts and silt-clay mixtures. Journal of Geotechnical and Geoenvironmental Engineering, 125(8): 706-710. DOI:10.1061/(ASCE)1090-0241(1999)125:8(706) (  0) 0) |
Jaeger, R. A., 2012. Numerical and experimental study on cone penetration in sands and intermediate soils. PhD thesis. University of California Davis.
(  0) 0) |
Jaeger, R. A., DeJong, J. T., Boulanger, R. W., Low, H. E., and Randolph, M. F., 2010, Variable penetration rate CPT in an intermediate soil. The Proceedings of 2nd International Symposium on Cone Penetration Testing. Huntington Beach, 1-9.
(  0) 0) |
Kim, K., 2005. Cone penetration test in clayey soil: Rate effect and application to pile shaft resistance calculations. PhD thesis. Purdue University.
(  0) 0) |
Kim, K., Prezzi, M., Salgado, R., A., and Lee, W.. 2008. Effect of penetration rate on cone penetration resistance in saturated clayey soils. Journal of Geotechnical and Geoenvironmental Engineering, 134(8): 1142-1153. DOI:10.1061/(ASCE)1090-0241(2008)134:8(1142) (  0) 0) |
Krage, C. P., Broussard, N. S., and Dejong, J. T., 2014. Estimating rigidity index (IR) based on CPT measurements. The Proceedings of 3rd International Symposium on Cone Penetration Testing. Las Vegas, 1-11.
(  0) 0) |
Lehane, B. M., O'Loughlin, C. D., Gaudin, C., and Randolph, M. F.. 2009. Rate effects on penetrometer resistance in kaolin. Géotechnique, 59(1): 41-52. DOI:10.1680/geot.2007.00072 (  0) 0) |
Lunne, T., and Andersen, K. H., 2007. Soft clay shear strength parameters for deepwater geotechnical design. The Proceedings of 6th International Offshore Site Investigation and Geotechnics Conference. London, 151-176.
(  0) 0) |
Lunne, T., Robertson, P., and Powell, J.. 1997. Cone Penetration Testing in Geotechnical Practice. CRC Press, London, 352pp.
(  0) 0) |
Mahmoodzadeh, H., and Randolph, M. F.. 2014. Penetrometer testing-effect of partial consolidation on subsequent dissipation response. Journal of Geotechnical and Geoenvironmental Engineering, 140(6): 04014022. DOI:10.1061/(ASCE)GT.1943-5606.0001114 (  0) 0) |
Mahmoodzadeh, H., Randolph, M. F., and Wang, D.. 2014. Numerical simulation of piezocone dissipation test in clays. Géotechnique, 64(10): 848-850. DOI:10.1680/geot.2014.64.10.848 (  0) 0) |
Mo, P. Q., Gao, X. W., Yang, W. B., and Yu, H. S.. 2020. A cavity expansion-based solution for interpretation of CPTu data in soils under partially drained conditions. International Journal for Numerical and Analytical Methods in Geomechanics, 44(7): 1053-1076. DOI:10.1002/nag.3050 (  0) 0) |
Monforte, L., Arroyo, M., Carbonell, J. M., and Gens, A.. 2018. Coupled effective stress analysis of insertion problems in geotechnics with the particle finite element method. Computers and Geotechnics, 101: 114-129. DOI:10.1016/j.compgeo.2018.04.002 (  0) 0) |
Poulsen, R., Nielsen, B. N., and Ibsen, L. B., 2013. Correlation between cone penetration rate and measured cone penetration. The Proceedings of 18th International Conference on Soil Mechanics and Geotechnical Engineering. Paris, 603-606.
(  0) 0) |
Randolph, M. F., and Hope, S. F., 2004. Effect of cone velocity on cone resistance and excess pore pressures. The Proceedings of Engineering Practice and Performance of Soft Deposits. Osaka, 147-152.
(  0) 0) |
Salgado, R., Prezzi, M., Kim, K., and Lee, W., 2010. Penetration rate effects on cone resistance measured in a calibration chamber. 4th International Conference on Site Characterization, ISC'4. Pernambuco, 1-6.
(  0) 0) |
Schneider, J. A., Lehane, B. M., and Schnaid, F.. 2007. Velocity effects on piezocone measurements in normally and over consolidated clays. International Journal of Physical Modelling in Geotechnics, 7(2): 23-34. DOI:10.1680/ijpmg.2007.070202 (  0) 0) |
Silva, M. F., 2005. Numerical and physical models of rate effects in soil penetration. PhD thesis. University of Cambridge.
(  0) 0) |
Silva, M. F., White, D. J., and Bolton, M. D.. 2006. An analytical study of the effect of penetration rate on piezocone tests in clay. International Journal for Numerical and Analytical Methods in Geomechanics, 30(6): 501-527. DOI:10.1002/nag.490 (  0) 0) |
Song, B. H., Sun, Y. F., and Song, Y. P.. 2020. Post-liquefaction re-compaction effect on the cyclic behavior of natural marine silty soil in the Yellow River Delta. Ocean Engineering, 195: 106753. DOI:10.1016/j.oceaneng.2019.106753 (  0) 0) |
Stewart, D. P., 1990. Lateral loading of piles in soft clay due to nearby embankment construction. Research Report GEO: 900 86. The University of Western Australia.
(  0) 0) |
Suzuki, Y., 2010. Numerical analysis of in-situ testing in under-consolidated clay. Master thesis. Kobe University.
(  0) 0) |
Suzuki, Y., 2015. Investigation and interpretation of cone penetration rate effects. PhD thesis. University of Western Australia.
(  0) 0) |
Suzuki, Y., and Lehane, B. M.. 2015. Cone penetration at variable rates in kaolin-sand mixtures. International Journal of Physical Modelling in Geotechnics, 15(4): 209-219. DOI:10.1680/ijpmg.14.00043 (  0) 0) |
Tolooiyan, A., and Gavin, K.. 2011. Modelling the cone penetration test in sand using cavity expansion and arbitrary lagrangian eulerian finite element methods. Computers and Geotechnics, 38: 482-490. DOI:10.1016/j.compgeo.2011.02.012 (  0) 0) |
Wang, D., Randolph, M. F., and Gourvenec, S., 2015. Coefficient of consolidation for soil-that elusive quantity. The Proceedings of VI International Conference on Computational Methods for Coupled Problems in Science & Engineering. Venice, 1218-1231.
(  0) 0) |
Xu, X., 2007. Investigation of the end bearing performance of displacement piles in sand. PhD thesis. The University of Western Australia.
(  0) 0) |
Xu, X., and Lehane, B.. 2008. Pile and penetrometer end bearing resistance in two-layered soil profiles. Géotechnique, 58(3): 187-198. DOI:10.1680/geot.2008.58.3.187 (  0) 0) |
Yang, Z. N., Zhu, Y. M., Liu, T., Sun, Z. Q., Ling, X. Z., and Yang, J. M.. 2019. Pumping effect of wave-induced pore pressure on the development of fluid mud layer. Ocean Engineering, 189: 106391. DOI:10.1016/j.oceaneng.2019.106391 (  0) 0) |
Yi, J. T., Goh, S., and Lee, F. A.. 2012. Numerical study of cone penetration in fine-grained soils allowing for consolidation effects. Géotechnique, 62(8): 707-719. DOI:10.1680/geot.8.P.155 (  0) 0) |
Yu, H. S., 2000. Cavity Expansion Methods in Geomechanics. Kluwer Academic Publishers, The Netherlands, 33-46.
(  0) 0) |
Zhao, D. D., Cheng, H. Y., Lin, F. S., Qin, X. K., Zhu, X. H., Chen, X. C., et al.. 2020. Triggering factors of submarine landslide in the Yellow River Delta: Take the Chengdao area as an example. Marine Geology Frontiers, 36(7): 25-30. (  0) 0) |
Zhou, Q. J., Jia, Y. G., Ma, D. C., Shan, H. X., and Liu, H. J.. 2006. Research of consolidating inhomogeneity of silt seabed in Yellow River Estuary shore. Rock and Soil Mechanics, 27(7): 1147-1152 (in Chinese with English abstract). (  0) 0) |
 2022, Vol. 21
2022, Vol. 21


