2. 中国海洋大学 海洋发展研究院, 山东 青岛 266100;
3. 中央财经大学 国际经济与贸易学院, 北京 102206
2. Marine DevelopmentResearchInstitute, Ocean University of China, Qingdao 266100, China;
3. School of International Economics and Trade, Central University of Finance and Economics, Beijing 102206, China
产业集聚是指同一产业或相关产业在某个特定地理区域内高度集中, 不同要素在空间范围内不断汇聚的一个过程, 海洋产业集聚亦是如此。党的十九大报告指出, “坚持陆海统筹, 加快建设海洋强国”, 而海洋产业的空间集聚是实现陆海统筹的重要抓手。对于大国而言, 产业空间分布的不均衡以及由此形成的集聚现象是一种客观规律, 对于海洋产业也同样如此。较早关注海洋产业集聚现象的是韩增林等, 他认为, 我国海洋经济地区差异与多种海洋产业的同一空间集聚表现为相同的变动过程。[1]作为经济发展中的重要特征化事实, 产业集聚是一个历久弥新的研究主题。就行业属性而言, 对产业集聚的研究最初集中在制造业方面, 在这方面国内外已经积累了大量文献。[2][3][4][5][6][7][8]随着服务业在我国经济中地位的不断提高, 服务业的集聚日益受到关注。[9][10][11][12][13][14][15]相应地, 海洋经济的快速发展也使海洋产业集聚的研究蓬勃发展。
对于海洋产业集聚的普遍性和重要性, 相关学者认为, 随着海洋产业的发展, 产业集聚效应日益显现, [16]在经济一体化背景下, 集聚已成为现代海洋经济发展的基本形式, [17]沿海地区海洋经济发展中存在着产业集聚现象; [18]对于海洋产业集聚的研究首先应该解释集聚形成原因, 主要观点包括:李青等认为, 导致海洋产业空间集聚变动的主要原因是资源禀赋、发展基础和发展条件的变化; [19]高源指出, 海洋产业集聚的时空特征是各因素、各层次系统内部与系统之间复杂作用及循环累积效应作用下的外在表现。[20]当然, 研究的重点还是海洋产业集聚与区域发展及资源环境间的关系, 其主要观点又分为两方面:一是海洋产业集聚的正面作用, [21][22][23][24][25]二是海洋产业集聚的负面作用。[26][27]这就产生了海洋经济的协调发展问题, 对此朱凌等认为, 要充分发挥区域海洋产业集聚优势, 使区域形成相互依赖、合理分工、协调发展的海洋经济统一体; [28]同样, 杨晓峰等提出, 应着力培育海洋新兴产业, 优化现代海洋产业集聚带的空间布局。[29]
总体而言, 上述关于海洋产业集聚不同方面的文献构成了本文研究的重要基础, 但仍存在拓展与深化的空间。在我国各类海洋产业快速发展的背景下, 其所呈现出的集聚态势也越来越明显。海洋资源具有整体性、流动性和使用多样性等特点, 加之我国地区经济发展水平差异性较大。因此, 根据海洋资源禀赋的差异以及不同地区的区位特征, 选择并匹配与之相宜的海洋产业集聚水平, 做到既发挥集聚效应又避免因集聚过度或不足而造成效率损失, 是我国海洋经济发展中的重要问题。
作为大国, 我国在经济治理上长期采取分权治理模式以激励地方政府发展本地区经济。对于我国海洋产业集聚来说, 中央政府的目标是从整体利益出发, 通过更好地发挥集聚效应以实现海洋经济的可持续发展。但地方政府会考虑本地区经济利益, 在区域博弈中采取非市场手段引发海洋经济的无序与恶性竞争, 导致产业集聚过度或不充分。在这一背景下, 不同层级的政府间存在两类博弈关系:一类是中央政府与地方政府, 一类是不同地方政府之间。因此, 从政府博弈的视角对我国海洋产业集聚进行研究非常必要。相比以往研究, 本文的贡献是:第一, 从我国的大国特征出发, 根据海洋产业集聚特点及区域效应, 考虑经济利益与政治晋升两个角度, 构建了双重政府博弈模型; 第二, 按照完全信息和不完全信息两种情况, 分析了双重政府博弈下合意海洋产业集聚实现所需具备的条件及存在的难点。
二、基本假定与博弈模型构建 (一) 基本假定1、研究背景假定
大国经济的显著特征之一是区域经济发展水平存在较大差异。假设在一个大国内部, 有a、b两个相邻沿海地区和m、n两种海洋资源, 由两种海洋资源的开发利用可形成M、N两类海洋产业, a地区经济发展水平远高于b地区。
对于海洋资源m来说, a地区的资源数量大于b地区的资源数量, 即ma>mb; 对于海洋资源n来说, b地区的资源数量大于a地区的资源数量, 即na<nb。a地区经济发展水平高, 且在海洋产业M方面拥有海洋资源禀赋优势, 在适度的政策扶持下能形成较高的海洋产业集聚水平; 对于海洋产业N, a地区虽无海洋资源禀赋优势, 但得益于较高的经济发展水平与雄厚的政府财力, 其集聚水平并不会落后。b地区在发展海洋产业M方面, 海洋资源禀赋、地区经济发展水平、地区财政资金规模均处劣势, 寻求利益最大化的地方政府不会将有限的资金用于扶持海洋产业M发展; 而对于海洋产业N, b地区拥有海洋资源禀赋优势, 且产业集聚过程中拥挤效应弱, 故其发展海洋产业N的意愿强烈。
2、博弈模型假定
假设1:博弈的参与方为a地区政府、b地区政府与中央政府, 三者均完全理性。a、b地区政府追求自身效用最大化。这包括两层含义:一是经济利益, 即通过海洋产业集聚促进本地区海洋经济的发展; 二是以此为基础实现地区官员的政治晋升。中央政府从全局出发进行a、b地区间的调控, 通过海洋产业集聚实现区域海洋经济的协调与可持续发展。
假设2:i地区产业集聚度表示为如下函数关系:Bi=ni(μi+βi), 其中ni代表i地区海洋资源禀赋状况, μi代表i地区海洋产业经济效率, βi代表i地区政策环境①。据此, 本文将地区海洋产业集聚面临的特定政策环境用财政投资资金规模来表示, 即i地区海洋产业面临的政策环境为:βi=Ii-γIj+Ici, (i=a, j=b; i=b, j=a)。Ii、Ij、Ici分别表示i地区政府、j地区政府对本地海洋产业的投资及中央政府对i地区海洋产业的投资; 系数γ代表地区政府对本地区海洋产业投资对另一地区政策环境的边际影响, 即各地区政府通过投资争夺海洋产业发展资源, 若γ不为0, 则认为边际影响存在, 且假定|γ|≤1。[30]
① 此处海洋产业经济效率表示在资源环境约束下海洋产业的可持续发展, 与下文提出的最优产业集聚水平呈正相关关系。
假设3:i地区以海洋产业集聚实现的海洋经济总产出是关于财政投资资金η的函数, 且满足边际报酬递减规律, 可表示为:Yi=vηic, 且c∈(0, 1)。其中, v为财政投资的回报系数, c表示财政投资的产出弹性系数。
假设4:海洋产业集聚与区域海洋经济发展有着密切关系, 相对产业集聚度Bi-Bj直接反映了两地区海洋经济的发展差距, 这可以表示i地区因集聚所带来的相对海洋经济业绩。
假设5:海洋产业空间集聚同时面临集聚效应与拥挤效应, 随着海洋产业集聚度的提高, 海洋产业集聚度与区域海洋经济发展呈现倒“U”型关系。假定b地区海洋资源禀赋丰裕, 发展相关海洋产业面临的资源约束弱, 而a则相反。用B、B0分别表示地区实际与最优海洋产业集聚度, b地区最优海洋产业集聚度B0b高于a地区最优海洋产业集聚度B0a。若用A、D代表在最优海洋产业集聚度下a、b两地区海洋产业经济发展达到的最高水平, 则a、b地区区域海洋经济的实际发展水平分别为:A-(Ba-B0a)2、D-(Bb-B0b)2。
假设6:中央政府关注两地区海洋经济的实际发展水平, 并期望通过中央政府的财政投资推动两地区海洋经济发展达到最优水平。用x、(1-x)分别表示a、b地区海洋经济实际发展水平在中央政府效用函数中的权重, 其中x∈(0, 1)。
根据假设可得地区政府函数以及中央政府效用函数。
(1) a、b地方效用函数
根据假设4, i地区政府效用函数由两部分组成:一是经济利益, 由海洋产业集聚的总产出也就是财政投资资金回报表示; 二是地方官员的政治晋升, 由i地区海洋产业的相对产业集聚度表示。公式为:
| $ {U_i} = \alpha \left( {v\eta _i^c - {I_i}} \right) + \beta \left( {{B_i} - {B_j}} \right) $ |
式中, α、β分别表示经济收益与政治晋升效用系数。[30]
(2) 中央政府效用函数
中央政府效用函数可以表示为:
| $ {U_c} = x\left[ {A - {{\left( {{B_a} - B_0^a} \right)}^2}} \right] + (1 - x)\left[ {D - {{\left( {{B_b} - B_0^b} \right)}^2}} \right]{\rm{s}}{\rm{.t}}{\rm{. }}\quad I_c^a + I_c^b \le E $ |
式中, E为既定的投资支出; Ba=na[μa+(Ia+Ica-γIb)], 且ηa=Ia+Ica; Bb=nb[μb+(Ib+Icb-γIa)], 且ηb=Ib+Icb。
(二) 博弈模型构建周黎安指出, 我国由于经济分权治理形成了官员晋升的锦标赛模式, 地区之间为增长而竞争。[31]同样, 官员晋升锦标赛在区域海洋经济的发展过程中是否存在?沿海省份是否存在为地区海洋经济增长而竞争的现象?显然, 上述问题的答案与区域海洋经济发展中的海洋产业集聚紧密相关。
海洋产业集聚的形成是多种因素相互作用的结果。以海洋资源为基础, 在市场机制的作用下, 资本、劳动力和技术等可流动性生产要素会“追逐”海洋资源这类不可流动生产要素, 由此形成特有的海洋产业集聚这一客观经济现象。从政府角度来讲, 对于某一地区海洋产业集聚的形成, 中央政府与其他地区政府为间接参与者, 在信息完备性上处于劣势地位, 即中央政府与其他地区政府完全了解该地区的海洋资源禀赋状况, 但无法准确知晓该地区影响海洋产业集聚的海洋产业效率等。同时, 中央政府和地方政府之间以及地方各政府之间因利益的不一致性而存在博弈关系。
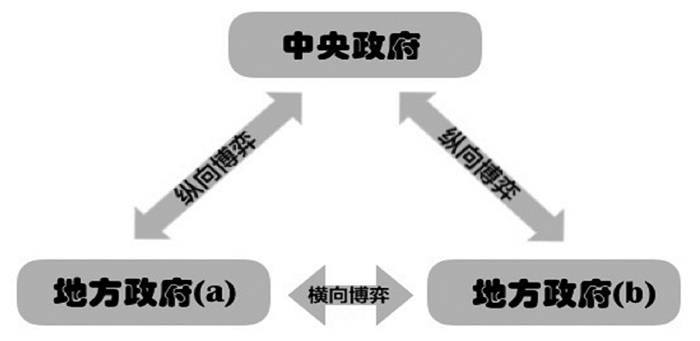
基于上述分析, 主导海洋产业集聚的政府主体在区域海洋经济发展过程中存在双重博弈关系(见图 1):一是中央政府和地方政府间的纵向博弈; 二是地方政府a和b之间的横向博弈。鉴于海洋生态系统的脆弱性, 假如a地区已经集聚过度, 会停止集聚吗?在信息不对称的情况下, 中央政府如何知道a地区或b地区已经集聚过度?在区域海洋经济竞争的条件下, 如何作出合意的选择以通过集聚实现海洋经济的高质量发展?对诸如上述问题的回答都体现在下文博弈模型的求解及均衡讨论中。
|
图 1 双重政府博弈模型 |
基于a地区海洋产业经济效率信息对于中央与其他地区政府是否完全为标准, 可以从完全信息与不完全信息两种情况展开分析。
(一) 完全信息情况下博弈模型求解及模型均衡讨论在完全信息的三方动态博弈中, a地区政府、b地区政府、中央政府依次行动, 实现自身效用最大化。利用逆向归纳法, 先求出中央政府的最优投资额, 再回代b地区政府的最优投资规模, 最后得到a地区政府的最优投资规模, 从而得到博弈的子博弈精炼纳什均衡(SPNE)。②[32][33]
② 限于篇幅, 文中公式的推导过程均已省略, 若需要了解详细推导过程, 可以向作者索取。
我们用t替代a地区与b地区发展该海洋产业经济的政治偏重系数比与海洋资源禀赋比例平方的乘积, 即
| $ \begin{array}{l} I_a^* = \frac{{1 + \gamma t\left( {{W_b} - E} \right) - t(1 - \gamma ){W_a} + {W_c}}}{{\gamma (1 + t)}};\quad I_b^* = \frac{{ - (1 - \gamma )\left( {{W_b} - E} \right) + (t + \gamma ){W_a} - {W_c}}}{{\gamma (1 + t)}};\\ I_c^{a*} = \frac{{ - (1 + \gamma t)\left( {{W_b} - E} \right) + (t + \gamma ){W_a} - {W_c}}}{{\gamma (1 + t)}}。\end{array} $ |
其中,
首先, 考虑最优海洋产业集聚度B0i(i=a, b), 根据模型的均衡解可以得到:
| $ \frac{{\partial I_a^*}}{{\partial B_0^a}} > 0, \frac{{\partial I_a^*}}{{\partial B_0^b}} < 0;\frac{{\partial I_b^*}}{{\partial B_0^b}} > 0, \frac{{\partial I_b^*}}{{\partial B_0^a}} < 0 $ | (1) |
| $ \frac{\partial I_{c}^{a *}}{\partial B_{0}^{a}}<0, \frac{\partial I_{c}^{a *}}{\partial B_{0}^{b}}>0 ; \frac{\partial I_{c}^{b *}}{\partial B_{0}^{b}}<0, \frac{\partial I_{c}^{b *}}{\partial B_{0}^{a}}>0 $ | (2) |
由式(1)、式(2)得到中央政府、地方政府关于海洋产业集聚博弈的命题1:
在其他影响因素不变的情况下, 当
对命题1的进一步解释:
对于a、b任一地区而言, 其某类海洋产业最优集聚度越高, 面临的海洋资源环境约束就相对越弱, 出于财政收益与政治晋升的考虑, 地方政府对此类海洋产业的支持力度就会增加。出于两地区间竞争的考虑, 如果另一地区此类海洋产业最优集聚度高于本地区, 则本地区促进这一海洋产业集聚的激励就会减弱, 这是因为, 如果预期到本地区不管如何发展该类产业都不可能超越另一地区, 其最优的选择是形成错位, 也就是减少对此类海洋产业的支持而形成其他产业的集聚。
中央政府则要在资源环境约束的条件下实现a、b两地区海洋产业的最优集聚。由于最优集聚度高的地区当地政府的支持力度很大, 中央政府没有必要对其加大支持; 相反, 对于海洋产业最优集聚度低的地区, 地方政府的积极性不高, 中央政府的支持十分必要。
命题1指出, 相对于中央政府, 地方政府对于海洋产业集聚更注重挖掘本地区海洋经济发展潜力。地区政府更愿意扶持最优集聚度高的海洋产业, 从而获得政治晋升与财政收益; 此时, 地区政府投资的替代效应大于中央政府的投资意愿, 也就出现了地区政府投资增加而中央政府投资减少的现象。相反, 最优海洋产业集聚低, 地区政府反而“知难而退”, 此时, 中央政府投资的替代效应大于地区政府的投资意愿, 地区政府投资减少而中央政府投资增加。
其次, 考虑μi(i=a, b), 根据模型的均衡解可以得到:
| $ \frac{{\partial I_a^*}}{{\partial {\mu _a}}} < 0, \frac{{\partial I_a^*}}{{\partial {\mu _b}}} > 0;\frac{{\partial I_b^*}}{{\partial {\mu _b}}} < 0, \frac{{\partial I_b^*}}{{\partial {\mu _a}}} > 0 $ | (3) |
| $ \frac{{\partial I_c^{a*}}}{{\partial {\mu _a}}} > 0, \frac{{\partial I_c^{a*}}}{{\partial {\mu _b}}} > 0;\frac{{\partial I_c^{b*}}}{{\partial {\mu _b}}} > 0, \frac{{\partial I_c^{b*}}}{{\partial {\mu _a}}} < 0 $ | (4) |
由式(3)、式(4)得到中央政府、地方政府关于海洋产业集聚博弈的命题2:
在其他影响因素不变的情况下, 当
对命题2的进一步解释:
如果说命题1是直接说明了中央政府和地方政府关于海洋产业集聚的博弈关系, 那么命题2则是从间接角度对上述博弈关系的进一步分析, 这是因为, 地区政府对海洋产业的投资或支持力度与海洋产业效率有密切关系。
海洋产业经济效率反映了该地区海洋产业发展的资源约束与环境成本, 经济效率越高, 资源约束与环境成本越低, 其最优海洋产业集聚水平也就越高。由式(3)、式(4)可知, 当
相比较于地区政府, 中央政府面临投资选择时更注重本地区海洋产业经济效率。由式(4)可知, 海洋产业经济效率高的地区, 中央政府投资替代效应超过了地区政府增加的投资意愿, 从而中央政府投资增加、地区政府投资减少; 而地区海洋产业经济效率低的地区, 中央政府投资减少, 地区政府投资增加, 海洋资源遭过度开发与利用。
(二) 不完全信息情况下模型均衡求解及均衡讨论自然选择a地区在形成海洋产业集聚时有两种潜在类型:高经济效率型(μH), 概率为p(θ); 低经济效率型(μL), 概率为1-p(θ)。若a地区政府选择Ia, b地区政府与中央政府根据后验概率选择最优策略。在完全信息情况下, a地区政府出资存在最优规模Ia*, 使a地区政府效用最大化U*。对于a地区政府而言, 其希望中央政府增加出资而不愿看到b地区政府提高出资展开竞争。由于
1、分离均衡
在分离均衡中, b地区政府及中央政府判断出a地区的真实经济效率类型。
(1) 当a地区政府出资策略为Ial时, 其为高经济效率型地区政府, 对应的贝叶斯精炼纳什均衡解为
(2) 当a地区政府出资策略为Iah时, 其为低经济效率型地区政府, 对应的贝叶斯精炼纳什均衡解为
2、混同均衡
在混同均衡下, a地区政府通过降低海洋产业投资规模发送信号, 成功隐瞒效率类型。
在这个博弈中, 不同类型的政府采取相同的出资策略, 即出资Ial。此时, 存在混同均衡
在分离均衡与混同均衡中, 各方关于特定海洋产业投资规模与完全信息情况下的差异源于中央政府与经济欠发达地区政府对经济发达地区政府类型的判断根据不完全信息与完全信息情况下模型均衡的比较, 可以得到以下结论:
| $ \frac{{\partial \left( {{I_a} + I_a^c - \gamma {I_b}} \right)}}{{\partial {\mu _a}}} = - \frac{t}{{1 + t}} $ | (5) |
| $ \frac{{\partial \left( {{I_b} + I_b^c - \gamma {I_a}} \right)}}{{\partial {\mu _a}}} = \frac{t}{{1 + t}} $ | (6) |
| $ \frac{{\partial \left( {{I_a} + I_a^c - \gamma {I_b}} \right)}}{{\partial {\mu _b}}} = \frac{1}{{1 + t}} $ | (7) |
| $ \frac{{\partial \left( {{I_b} + I_b^c - \gamma {I_a}} \right)}}{{\partial {\mu _b}}} = - \frac{1}{{1 + t}} $ | (8) |
命题1:根据产业集聚度公式Bi=ni(μi+βi)可知, 在完全信息情况下, 在海洋产业集聚过程中, 该地区区域海洋经济政策环境正向影响力度与本地区发展该海洋产业经济效率成反比, 与其他地区发展该海洋产业经济效率成正比。在不完全信息的混同均衡中, 对于高经济效率型a地区, 各方投资规模的变化将提高a地区该海洋产业集聚度, 降低b地区该海洋产业集聚度; 对于低经济效率型a地区结论相反③。
③ 在式(5)、式(6)中, μa在完全信息情况下表示a地区发展特定海洋产业时的经济效率, 在不完全信息情况下表示中央政府与b地区政府对a地区经济效率类型的判断。
根据上述结论, 结合完全信息情况下的结论如表 1所示。
|
|
表 1 不同信息情况下海洋产业集聚的政府扶持力度与政策环境分析 |
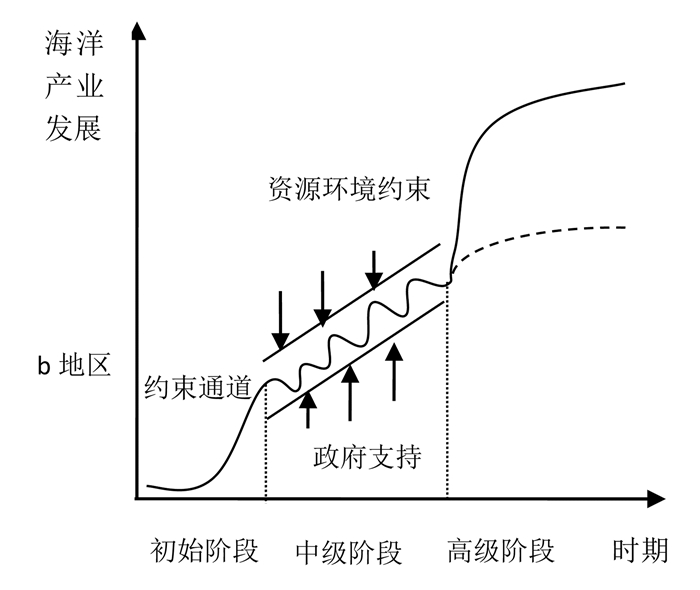
海洋产业集聚是区域海洋经济发展的重要推动力, 海洋产业集聚过程同时也是海洋产业发展的过程, 而政府在其中发挥着不可或缺的作用, 尤其是在海洋产业发展的初级、中级阶段(如图 3)。[34]国内外产业集聚经验表明, 产业集聚是自发产生的, 海洋产业也不例外; 在海洋产业集聚的最初阶段, 政府的产业政策作为诱导因素与扶持力量至关重要。海洋产业发展中级阶段是最不稳定但最关键的阶段, 只有通过“约束通道”才能实现海洋产业可持续发展。所以这一时期海洋产业发展存在困局:海洋产业发展虽能得到政府支持, 但也受到海洋资源环境约束。过度的政府支持将会引起高于最优规模的海洋产业集聚度, 导致海洋产业发展面临资源环境约束, 难以持续; 政府支持力度不够、长远规划与有力监管不够, 则会导致市场无序, 海洋产业发展后劲不足。两种局面下的海洋产业发展均难以向上进入“约束通道”, 也无法成功进入高级阶段(如图 3高级阶段虚线部分)。要实现海洋产业可持续发展, 政府行为在海洋产业集聚的中级阶段就应当适度, 即重点关注海洋产业集聚过程中的外部性问题, 致力于基础设施建设、环境污染治理等公共物品提供。[35]所以, 如果简单依照陆域经济模式将海洋经济发展纳入“政治晋升锦标赛”, 便会制约我国海洋产业的可持续发展。[36]
|
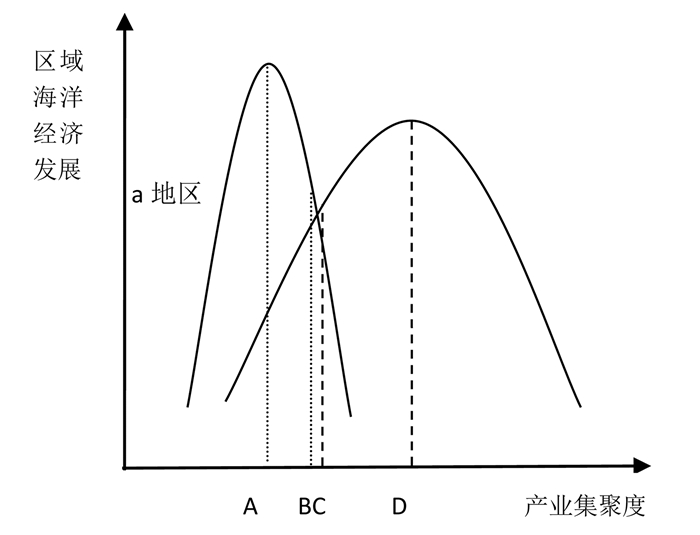
图 2 两地区海洋产业集聚度与海洋经济发展关系 |
|
图 3 海洋产业发展不同阶段与资源环境约束 |
从表 1可知, 在经济发展水平较高、地方财政充裕的地区, 地区政府出于政治晋升激励大力发展海洋产业, 加之欠发达地区经济竞争能力差, 因此其发展海洋产业的政策环境要远优于欠发达地区。政策环境的好坏并不能决定两地区海洋产业集聚度最终差距, 但可以反映两地区海洋产业发展面临的主要问题(图 2、图 3④):经济发达地区政策环境强, 实际海洋产业集聚度位于最优点A右侧B点处。该地区海洋产业经历初始阶段后, 进入中级阶段面临资源环境约束, 过高的产业集聚度使得该地区海洋资源开发处于“竭泽而渔”的状态, 难以通过“约束通道”进入高级阶段, 制约着海洋产业发展。经济欠发达地区虽然不会面临较强的环境资源约束, 但由于政策环境弱, 海洋产业集聚度位于最优点D点左侧C点处, 海洋产业发展在中级阶段缺乏政府长远规划、有力监管与财政支持等, 发展动力不足, 容易因市场无序引起海洋资源浪费与投资环境恶化。更为严重的是, 两地区的博弈易导致我国海洋产业集聚背离各地区的比较优势, 影响海洋产业发展的总体布局, 从而造成发达地区过度开发与欠发达地区投入不足的局面。
④ 在图 3中, 由于发达地区特定海洋产业发展潜力可能高于、低于或等于欠发达地区该海洋产业发展潜力, 故a地区曲线最高点与b地区曲线最高点大小关系并不确定。在现实中, 通常发达地区海洋产业发展潜力高于欠发达地区, 因此在不影响研究目的情况下本图采用这一大小关系。
鉴于上述情况, 中央政府的宏观调控在海洋产业集聚中就显得非常重要。通过以下命题可证明, 在完全信息情况下, 中央政府能在一定条件下实现两地区域海洋产业集聚最优状态。考虑Bi*-B0i⑤是否为零, 也就是地区海洋产业集聚水平能否在政府间博弈中达到最优。根据完全信息情况下模型的均衡解可知, 当满足式(9)或式(10)时, 中央调控能实现a地区或b地区海洋产业集聚度最优, 即:
⑤ 此处Bi*为Bi(Ii*, Ici*, Ij*), 即Ba*可表示为Ba(Ia*, Ica*, Ib*), Bb*可表示为Bb(Ib*, Icb*, Ia*)。
| $ E_a^* = \frac{1}{\gamma }\left[ {\left( {\frac{{B_a^0}}{{{n_a}}} + \frac{{B_b^0}}{{{n_b}}}} \right) - \left( {{\mu _a} + {\mu _b}} \right) + (\gamma - 1)\left( {{W_b} + {W_a}} \right)} \right] $ | (9) |
| $ E_b^* = \frac{1}{\gamma }\left[ {\left( {\frac{{B_0^a}}{{{n_a}}} - {\mu _a} + \frac{{B_0^b}}{{{n_b}}} - {\mu _b}} \right) - (1 - \gamma ){W_a} - (1 - t){W_b}} \right] $ | (10) |
当且仅当式(11)成立时, Ea*=Eb*, 中央调控实现两地区海洋产业集聚度最优, 即:
| $ \left. {\frac{{{W_a}}}{{{W_b}}} = \frac{{t - 1}}{{2(1 - \gamma }}} \right) - \frac{1}{2} $ | (11) |
命题2:中央政府宏观调控使两地区海洋产业集聚度达到最优需要满足三大条件:一是政府间信息传递机制能避免出现信息不完全情况; 二是中央政府足够重视该海洋产业发展, 财政投入规模满足式(9)或式(10)的要求; 三是只有在式(11)成立时, 中央政府调控才能同时实现两地区海洋产业集聚度最优。因此, 在地区政府追求经济利益与政治晋升的前提下, 中央政府仅仅依靠财政经济手段难以实现区域海洋经济发展水平的最优, 需要不断改革、调整海洋管理体制与投入, 满足以上三大制约因素。
对命题2进一步的解释为:
由于海洋资源具有整体性、较强流动性及使用多宜性等特征, 海洋产业集聚一方面要求对海洋资源进行综合开发与利用, 另一方面也面临着因各地区海洋资源组合相似而极易出现恶性竞争、重复建设等严重发展问题。在区域海洋经济发展进程中, 政府能否发挥积极作用推动海洋产业集聚达到最优, 在一定程度上依赖于海洋经济管理体制的变革。由上述公式可知, 地区政府的政治晋升激励与财政配置效率激励难以协调地区海洋产业集聚与区域经济发展关系, 中央依靠财政经济手段的调控即便在满足完全信息与充足财政投入情况下, 受客观条件制约也难以达到调控目标。
在现实情况中, 信息传递不畅与中央政府宏观调控力度不足一直是困扰我国海洋产业发展的重要问题。其中信息传递不畅尤为严重, 其背后在一定程度上反映出我国海洋管理体制长期存在的多方关系难以理顺问题。作为一个大国, 随着我国政府对海洋管理分工愈加精细化, 地区政府逐渐拥有了对特定海洋资源的控制权以及决策权, 从而形成了不同的利益主体。这一方面造成了中央政府与地方政府之间信息不畅, 进而导致交易成本增加; 另一方面也造成地区政府之间协调合作成本提高。同时, 在面临亟须发展海洋产业与越来越强的环境约束之间的矛盾局面下, 实现海洋产业适度集聚要求中央政府着重提高宏观调控与监管力度。
由于等式(11)是关于地区海洋经济实际发展水平在中央政府效用函数中权重系数(即系数x与(1-x))的函数, 中央政府为实现两地区海洋产业集聚度最优必须根据实际情况不断调整权重系数以使等式成立。除此以外, 海洋产业发展要求中央政府进一步转变原有激励机制, 加强对海洋综合管理机构的授权, 按行业划分管理职能, 以合理利用海洋资源、保护海洋环境, 从而更好地实现海洋产业集聚促进区域海洋经济发展。
四、结论及启示海洋产业集聚既是海洋产业发展过程中客观现象, 也是发展动力之源。在海洋产业集聚的形成过程中, 政府的作用不可忽视。从财政配置视角来看, 在经济发展中财力贫困地区政府往往扮演“掠夺之手”角色, 财力富足地区政府往往扮演“扶持之手”的角色。[37]而通过建立动态博弈模型, 我们分析比较了完全信息与不完全信息两种情况, 研究表明, 政府在海洋产业集聚中角色既有共通之处, 也有其特殊性:无论是经济欠发达地区政府还是经济发达地区政府, 其决策选择都兼有“扶持性”与“掠夺性”; 满足区域海洋产业发展要求的政府决策便是“扶持之手”, 否则海洋产业的发展会因缺乏扶持、引导与监管, 或因产业发展受干预过多、海洋资源开发严重而变得不可持续, “扶持之手”转变为“掠夺之手”。
在海洋产业集聚中, 政府财政投入与决策受多种因素共同作用, 其中最优海洋产业集聚度与地区海洋经济效率是政府之间博弈的焦点。在完全信息情况下, 政府财政投入与决策会使得各地区海洋产业发展背离比较优势原则, 海洋资源禀赋匮乏的经济发达地区海洋产业发展面临政府过强干涉的问题, 海洋资源禀赋富裕的经济欠发达地区海洋产业发展面临支持力度不足的窘境。中央政府宏观调控是否有效, 取决于其调控力度是否足够大, 取决于中央政府是否足够重视该海洋产业发展进而投入满足调控要求的财政资金, 还取决于地区海洋产业发展在中央政府效用函数中的相对重要性。不完全信息情况下的分离均衡提高了中央政府决策成本, 而混同均衡尽管降低了低经济效率地区政策环境影响力, 提高了高经济效率地区政策环境影响力, 但会导致中央政府的调控失效。鉴于此, 政府应当进一步转变激励机制, 加强综合管理与调控, 通过集聚实现区域海洋经济的高质量发展。
| [1] |
韩增林, 王茂军, 张学霞. 中国海洋产业发展的地区差距变动及空间集聚分析[J]. 地理研究, 2003, (3): 289-296. (  0) 0) |
| [2] |
Ellison Glaeser. Geographic Concentration in U. S. Manufacturing Industries: A Dartboard Approach[J]. Journal of Political Economy, 1997, 105(5): 889-927.
(  0) 0) |
| [3] |
粱琦. 产业集聚的均衡性和稳定性[J]. 世界经济, 2004, (6): 11-18. (  0) 0) |
| [4] |
路江涌, 陶志刚. 我国制造业区域集聚程度决定因素的研究[J]. 经济学(季刊), 2007, (3): 801-816. (  0) 0) |
| [5] |
范剑勇, 姚静. 对中国制造业区域集聚水平的判断——兼论地区间产业是否存在同构化倾向[J]. 江海学刊, 2011, (5): 89-94. (  0) 0) |
| [6] |
程艳, 叶徵. 流通成本变动与制造业空间集聚——基于地方保护政策的理论与实践分析[J]. 中国工业经济, 2013, (4): 146-158. (  0) 0) |
| [7] |
李雪松, 孙博文. 高铁开通促进了制造业集聚吗?——基于京广高铁的准自然实验研究[J]. 中国软科学, 2017, (7): 81-90. (  0) 0) |
| [8] |
陈阳, 唐晓华. 制造业集聚和城市规模对城市绿色全要素生产率的协同效应研究[J]. 南方经济, 2019, (3): 71-89. (  0) 0) |
| [9] |
胡晓鹏, 李庆科. 生产性服务行业的空间集聚与形成模式:长三角例证[J]. 改革, 2008, (9): 81-88. (  0) 0) |
| [10] |
王耀中, 任英华, 姚莉媛. 服务业集聚机理研究新进展[J]. 经济学动态, 2010, (4): 104-108. (  0) 0) |
| [11] |
原毅军, 宋洋. 服务业产业集聚与劳动生产率增长——基于中国省级面板数据的实证研究[J]. 产业经济评论, 2011, (6): 50-61. (  0) 0) |
| [12] |
张勇, 蒲勇健, 陈立泰. 城镇化与服务业集聚——基于系统耦合互动的观点[J]. 中国工业经济, 2013, (6): 57-69. (  0) 0) |
| [13] |
吴福象, 曹璐. 生产性服务业集聚机制与耦合悖论分析——来自长三角16个核心城市的经验证据[J]. 产业经济研究, 2014, (4): 13-21. (  0) 0) |
| [14] |
刘奕, 夏杰长, 李垚. 生产性服务业集聚与制造业升级[J]. 中国工业经济, 2017, (7): 24-42. (  0) 0) |
| [15] |
曾艺, 韩峰, 刘俊峰. 生产性服务业集聚提升城市经济增长质量了吗?[J]. 数量经济技术经济研究, 2019, (5): 83-100. (  0) 0) |
| [16] |
黄瑞芬, 王佩. 海洋产业集聚与环境资源系统耦合的实证分析[J]. 经济学动态, 2011, (2): 39-42. (  0) 0) |
| [17] |
傅远佳. 海洋产业集聚与经济增长的耦合关系实证研究[J]. 生态经济, 2011, (9): 126-129. (  0) 0) |
| [18] |
金炜博, 高强, 于水仙. 浙江省海洋产业集聚实证研究[J]. 东方企业文化, 2012, (24): 225-226. (  0) 0) |
| [19] |
李青, 张落成, 武清华. 江苏沿海地带海洋产业空间集聚变动研究[J]. 海洋湖沼通报, 2010, (4): 106-110. (  0) 0) |
| [20] |
高源, .我国海洋产业集聚时空特征、驱动机理及其与区域要素协调发展研究[D].大连: 辽宁师范大学, 2012.
(  0) 0) |
| [21] |
武鹏, 王镇, 周云波. 中国区域海洋经济发展水平综合评价[J]. 经济问题探索, 2010, (2): 26-32. (  0) 0) |
| [22] |
王双. 我国海洋经济的区域特征分析及其发展对策[J]. 经济地理, 2012, (6): 80-83. (  0) 0) |
| [23] |
栗坤, 徐伟祥, 刘美辰. 浙江省海洋产业集聚与经济增长的互动关系[J]. 经营与管理, 2013, (11): 119-122. (  0) 0) |
| [24] |
赵祥. 我国海洋产业集聚的实证分析[J]. 岭南学刊, 2013, (4): 98-103. (  0) 0) |
| [25] |
尹肖妮, 王国红, 周建林. 区域知识承载力与海洋新兴产业集聚耦合研究[J]. 华东经济管理, 2016, (9): 59-65. (  0) 0) |
| [26] |
王志红. 浙江海洋产业集聚与环境资源系统耦合分析[J]. 科技经济市场, 2012, (7): 19-22. (  0) 0) |
| [27] |
王涛, 何广顺, 宋维玲, 等. 我国海洋产业集聚的测度与识别[J]. 海洋环境科学, 2014, (4): 568-575. (  0) 0) |
| [28] |
朱凌, 王晓惠. 推进区域海洋经济协调发展的管理方式初探[J]. 海洋开发与管理, 2010, (1): 89-91. (  0) 0) |
| [29] |
杨晓峰, 徐光明. 现代海洋产业集聚带空间布局优化研究——以南通市沿海产业布局为例[J]. 盐城师范学院学报(人文社会科学版), 2019, (1): 24-29. (  0) 0) |
| [30] |
张晔, 刘志彪. 产业趋同:地方官员行为的经济学分析[J]. 经济学家, 2005, (6): 62-67. (  0) 0) |
| [31] |
周黎安. 晋升博弈中政府官员的激励与合作——兼论我国地方保护主义和重复建设问题长期存在的原因[J]. 经济研究, 2004, (6): 33-40. (  0) 0) |
| [32] |
Fudenberg. D, Tirole. J. Game Theory[M]. MIT Press, 1991.
(  0) 0) |
| [33] |
Osbone. M. J, Rubinstein. A. A Course in Game Theory[M]. MIT Press, 1994.
(  0) 0) |
| [34] |
纪玉俊. 资源环境约束、制度创新与海洋产业可持续发展[J]. 中国渔业经济, 2014, (4): 20-27. (  0) 0) |
| [35] |
姜旭朝, 黄聪. 海洋产业演化理论研究动态[J]. 经济学动态, 2008, (8): 94-98. (  0) 0) |
| [36] |
于思浩. 海洋强国战略背景下我国海洋管理体制改革[J]. 山东大学学报(哲学社会科学版), 2013, (6): 153-160. (  0) 0) |
| [37] |
皮建才. 转型时期地方政府公共物品供给机制分析[J]. 财贸经济, 2010, (9): 58-63. (  0) 0) |
 2020
2020 
