2. 中国海洋大学 海洋发展研究院,山东 青岛 266100
2. Research Institute of Marine Development, Qingdao 266100, China
湿地与森林、海洋并称为全球三大生态系统,其拥有很高的生态价值和经济价值,被誉为“生命的摇篮”“地球之肾”和“生物基因库”。滨海湿地得益于其天然的地理位置,拥有海陆的双重特性,资源供给多, 物质产出丰富,在缓冲海洋冲击、为人类提供生物资源和维持生物多样性等方面具有重要作用。
20世纪70年代之前,由于各个国家普遍缺少环境保护意识,湿地生态系统遭到破坏。随着经济社会不断发展,环境问题开始凸显,各国政府开始意识到人类同其环境的相互依存关系。自国际湿地公约于1971年2月2日签订时起,很多国家开始不断完善相关法律法规开展滨海湿地保护和修复工作。
我国自1992年加入湿地公约后, 相关的研究开始增多, 国家对于滨海湿地的重视力度也不断加大,相关部门制订了一系列滨海湿地合理发展政策。2016年,国家海洋局曾印发了《关于加强滨海湿地管理与保护工作的指导意见》,力争实现对滨海湿地生态系统的有效保护。2018年,国务院印发了《关于加强滨海湿地保护严格管控围填海的通知》,明确从严控新增围填海造地、加快处理围填海历史遗留问题、加强海洋生态保护修复、建立长效机制四个方面进一步提高滨海湿地保护水平,严格管控围填海活动。
滨海湿地绿色发展是经济社会绿色发展的重要组成部分,契合了我国生态系统文明建设的理念,更加符合经济社会可持续发展的要求。进行滨海湿地绿色发展效应评价研究有利于分析解决这一问题,滨海湿地的绿色发展对未来经济效应的增长有促进作用。
一、文献综述 (一) 绿色发展的相关文献分析20世纪50年代以后,人类意识到环境的重要性,有关专家学者开始建立相关的生态环境评价指标体系来深入分析如何实现绿色发展这一研究问题。美国经济学家鲍勃·霍尔(Bob Hall)和玛丽·李·克尔(Mary Lee Kerr)在《199—1992绿色指数—对各州环境质量的评价》一书中曾提出有关环境的绿色发展指数。国外学者对绿色经济的研究较早,这一概念是由Pearce提出的,其基于净国民生产总值(NNP)修正对绿色经济核算进行研究,并对资源环境要素的影响进行考虑。Hong S et al.、Marco-Fondevila et al.、Luukkanen J et al.分别以韩国、西班牙、老挝为研究对象,阐述了绿色经济发展与环境保护之间的关系。[1][2][3]中国政府对绿色经济理念的探索与发展也十分重视,党的十八届五中全会首次提出“绿色发展”理念,大量专家学者开始了对绿色经济发展等方面的研究。杜永强等、朱芬华研究中国绿色经济发展与资源利用状况,强调绿色发展的重要性;[4][5]王海军、邹日崧采用绿色经济评级指标对美国匹兹堡、丹麦哥本哈根及日本北九州三座典型城市绿色经济发展情况进行分析比较,以此为其他城市绿色发展战略规划作出参考。[6]
此外,部分学者集中于对资源领域绿色发展状况的研究。K et al运用人工神经网络(ANN)对世界绿色能源消费进行分析,提出了一种预测2050年世界绿色能源消耗的人工神经网络方法;[7]Georgia Makridou基于DEA方法分析了欧盟2003—2009年期间典型的五个能源密集型产业的能源使用效率;[8]李春友、何广銮通过构建矿产资源绿色开发利用评价指标体系,对矿产企业资源开发利用绩效作出评价, 推进矿产企业绿色发展;[9]聂弯借助对黑龙江省大庆市展开的实地调查,摸索了教育资源坏境束缚之下大庆培养低碳稳步发展新动能获得的实际效果及存有的主要难题,给出了从第一、第二、第三文化产业培养低碳稳步发展新动能的对策。[10]
(二) 滨海湿地绿色发展的相关文献分析国内外关于滨海湿地绿色发展的研究文献十分鲜见,大多数专家学者主要从滨海湿地可持续发展等角度进行研究。James G Titus指出,气候变化对滨海湿地的影响较为显著,引入市场模式来对滨海湿地进行保护,以此实现滨海湿地可持续发展目标;[11]Osland MJ et al.研究表明,土壤有机质和植物生产力的未来变化可能会影响湿地的稳定性,为滨海湿地资源的可持续性利用与保护提出了对策;[12]王爱军等、许国晶等、王迪等分别以厦门滨海湿地、黄河口滨海湿地、广东省海岛滨海湿地为研究对象,通过分析滨海湿地存在的问题,为滨海湿地实现可持续发展提出相应的建议;[13][14][15]徐建国等、刘玉安等则从政府角度分析了滨海湿地的科学保护方式,指出政府在滨海湿地可持续发展中的重要作用。[16][17]
还有一部分学者通过研究滨海湿地的生态系统价值来研究滨海湿地在实现低碳发展方面的重要作用。Virginia D Engle、Simpson LT et al.分别以墨西哥湾滨海湿地、美国东南部湿地为研究对象,指出滨海湿地生态系统能够抵御侵蚀,减少大气中的碳,具有较高的碳储存能力等等;[18-19]丁冬静等对东寨港红树林保护区滨海湿地的生态系统服务功能总价值进行了评估,指出滨海湿地的固碳价值、防风消浪蓄水调洪价值和促淤造陆价值是主要的服务功能价值;[20]李楠、李龙伟等对杭州湾滨海湿地生态系统服务价值进行了评估,得出相似结论,即滨海湿地生态系统具有固碳价值、资源供给等价值,但是近年来由于不合理的人类活动,导致该生态系统服务总价值等呈递减趋势。[21]
综上所述,目前国内外学者对滨海湿地绿色发展的研究,多关注影响滨海湿地绿色发展的因素,特别将滨海湿地可持续发展的实现路径作为研究重点,但极少有文献研究有关滨海湿地绿色发展效应的评价。目前,国内学者开始探讨滨海湿地生态系统服务价值,将各方面的生态价值进行量化,并探究其变化趋势。总体而言,国内关于滨海湿地绿色发展效应评价的研究尚处于起步阶段,亟需更深入地探究。
基于以上研究现状,本文以中国沿海地区典型滨海湿地——黄河三角洲为研究对象,通过构建综合评价指标体系,运用多层次模糊分析以及灰色聚类分析等方法,对黄河三角洲绿色发展水平进行测度,在此基础之上,通过构造高质量定基发展综合指数,探索黄河三角洲2012—2018年的绿色发展变化趋势,并为其未来的可持续发展提供有针对性的政策建议。
二、滨海湿地绿色发展效应评价指标体系 (一) 评价指标体系构建李晓西在《中国绿色发展指数的编制》中介绍了绿色发展评价指标体系的构建方式。[22]本文在此基础之上,结合本文的研究目的,主要从经济增长绿化度、资源环境承载力、政府政策支持度三个方面来加以阐述,构建了一个由30个指标组成的黄河三角洲滨海湿地绿色发展效应评价指标体系,如表 1所示。
|
|
表 1 滨海湿地绿色发展效应评价指标体系 |
本文主要以黄河三角洲滨海湿地为研究对象,黄河三角洲湿地是我国境内比较典型的几大湿地之一,也是我国仅有的几个世界级的河口湿地生态系统。从地理位置上来看,黄河三角洲位于渤海南部黄河入海口沿岸地区, 包括山东省的东营、滨州和潍坊、德州、淄博、烟台市的部分地区,由于其中东营所占据的保护区面积相对较大,因此我们选择东营市的各指标数据作为评价模型。以上指标的原始数据来源于山东省统计局、东营统计局所发布的2012—2018年的《统计年鉴》,以及东营环保局、气象局所发布的数据。
(三) 数据描述性统计各指标的描述性统计如表 1。
四、滨海湿地绿色发展效应测度 (一) 基于多层次模糊分析的效应测度绿色发展效应的考核需要从多个方面对该地区作出客观全面的评论,因而实际上属于多目标决策问题。在绿色发展效应各指标的考核中存在了大量的模糊的概念,这导致了这些指标无法进行直接地量化,只能定性的考察,因此我们采用多层次模糊评价法进行绿色发展效应测度。
1、原始数据处理根据各数据库以及统计局信息,数据整理如表 2。
|
|
表 2 东营市绿色发展效应考核指标体系及考核表 |
第一,根据德尔菲法得到各级指标权重。
一级指标权重为:
A=[0.4, 0.3, 0.3]
二级指标权重为:
A1=[0.5, 0.5]
A2=[0.5, 0.5]
A3=[0.5, 0.5]
三级指标权重为:
A11=[0.15, 0.2, 0.15, 0.15, 0.15, 0.2]
A12=[0.2, 0.15, 0.15, 0.15, 0.2, 0.15]
A22=[0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1]
A21=[0.4, 0.3, 0.3]
A31=[0.5, 0.5]
A32=[0.3, 0.3, 0.4]
第二,根据表 2中数据我们可知,各个三级指标评判矩阵为:
| $ \begin{align} & {{M}_{11}}=\left[ \begin{array}{*{35}{l}} \ 0.5 & 0.375 & 0.125 \\ \ 0.3 & \ 0.3 & \ 0.4 \\ 0.625 & 0.125 & \ 0.25 \\ 0.375 & \ 0.25 & 0.375 \\ \ 0.3 & \ 0.55 & \ 0.15 \\ \ 0.7 & \ 0.15 & \ 0.15 \\ \end{array} \right]~\ \ {{M}_{12}}=\left[ \begin{array}{*{35}{l}} 0.45 & 0.25 & \ 0.3 \\ 0.15 & 0.55 & \ 0.3 \\ 0.45 & \ 0.4 & 0.15 \\ \ 0.6 & \ 0.1 & \ 0.3 \\ \ 0.3 & \ 0.4 & \ 0.3 \\ \ 0.6 & \ 0.3 & \ 0.1 \\ \end{array} \right]\ \ {{M}_{21}}=\left[ \begin{array}{*{35}{l}} 0.45 & 0.45 & \ 0.1 \\ \ 0.6 & 0.15 & 0.25 \\ 0.15 & 0.55 & \ 0.3 \\ \end{array} \right] \\ & {{M}_{22}}=\left[ \begin{array}{*{35}{l}} \ 0.3 & 0.55 & 0.15 \\ 0.45 & 0.32 & 0.23 \\ 0.43 & 0.25 & 0.32 \\ 0.56 & 0.21 & 0.23 \\ 0.65 & 0.15 & \ 0.2 \\ 0.35 & 0.45 & \ 0.2 \\ 0.45 & \ 0.3 & 0.25 \\ 0.35 & \ 0.5 & 0.15 \\ 0.43 & \ 0.3 & 0.27 \\ \end{array} \right]\ \ {{M}_{31}}=\left[ \begin{array}{*{35}{l}} 0.57 & 0.23 & \ 0.2 \\ \ 0.7 & 0.15 & 0.15 \\ \end{array} \right]\ \ {{M}_{32}}=\left[ \begin{array}{*{35}{l}} 0.43 & 0.57 & \ 0 \\ 0.43 & 0.27 & 0.3 \\ \ 0.3 & \ 0.4 & 0.3 \\ \end{array} \right] \\ \end{align} $ |
第三,对各个三级指标进行一级模糊综合评判得到:
B11=A11·M11=[0.47, 0.285, 0.245]
B12=A12·M12=[0.42, 0.3325, 0.2475]
B21=A21·M21=[0.405, 0.39, 0.205]
B22=A22·M22=[0.43, 0.338, 0.23]
B31=A31·M31=[0.635, 0.19, 0.175]
B32=A32·M32=[0.378, 0.412, 0.21]
因此,二级指标的评价矩阵为:
| $ \begin{align} & {{\text{M}}_{1}}=\left[ \begin{matrix} {{\text{B}}_{11}} \\ {{\text{B}}_{12}} \\ \end{matrix} \right] \\ & {{\text{M}}_{2}}=\left[ \begin{matrix} {{\text{B}}_{21}} \\ {{\text{B}}_{22}} \\ \end{matrix} \right] \\ & {{\text{M}}_{3}}=\left[ \begin{matrix} {{\text{B}}_{31}} \\ {{\text{B}}_{32}} \\ \end{matrix} \right] \\ \end{align} $ |
第四,对各个二级指标进行二级模糊综合评价得:
B1=A1·M1=[0.445, 0.3087, 0.2463]
B2=A2·M2=[0.4175, 0.364, 0.2175]
B3=A3·M3=[0.5065, 0.301, 0.1925]
因此,一级指标的评价矩阵为:
| $ \text{M}=\left[ \begin{matrix} {{\text{B}}_{1}} \\ {{\text{B}}_{2}} \\ {{\text{B}}_{3}} \\ \end{matrix} \right] $ |
第五,对各个一级指标进行三级模糊综合评价得:
B=A·M=[0.4552, 0.323, 0.2215]
3、模型结果的分析在模糊评判的过程中我们利用了软件Matlab计算相应的矩阵求积,根据三级指标综合评判结果可知,相应的评价等级—隶属度表见表 3。
|
|
表 3 隶属度表 |
由表 3可知,处于良好等级的概率最大,因此,根据最大隶属度原则,通过2018年的相关数据近似可得黄河三角洲湿地地区2018年度的绿色发展效应等级为良好。
(二) 基于灰色聚类评估模型的效应测度 1、基于端点混合可能度函数的灰色聚类评估模型假设有n个评价对象,m个评价指标,设xij(i=1, 2, …, n;j=1, 2, …, m)为评价对象i关于评价指标j的观测值,每一个评价指标作为一个灰数可以划分为s个灰类,fjk(·)(j=1, 2, …, m;k=1, 2, …, s)为j指标k子类可能度函数。此时给定的第j个指标的权重为(ηjk, j=1, 2, …, m;k=1, 2, …, s)。其建模步骤如下:
第一步:按照评估要求所需划分的灰类数s,将各个指标的取值范围也相应地划分为s个灰类。例如,将j指标的取值范围[a1, as+1]划分为s个小区间[a1, a2],…,[ak-1, ak],…,[as-1, as],[as, as+1]。
第二步:确定与[a1, a2]和[as, as+1]对应的灰类1和灰类s的转折点λj1,λjs;同时计算其余各个小区间的几何中点,λk=(ak+ak+1)/2,k=2, …, s-1。
第三步:对于灰类1和灰类s,构造相应的下限测度可能度函数fj1[-, -, λj1, λj2]和上线测度可能度函数fjs[λjs-1, λjs, -, -]。
设x为指标j的一个观测值,当x∈[a1, λj2]或x∈[λ1s-1, as+1]时,可分别由公式(1)和公式(2)计算出其属于灰类1和灰类s的可能度值fj1和fjs。
| $ f_{j}^{1}\left( x \right)=\left\{ \begin{array}{*{35}{l}} \ \ \ \ \ 0 & x\notin \left[ {{a}_{1}}, \lambda _{j}^{2} \right] \\ \ \ \ \ \ 1 & x\in [{{a}_{1}}, \lambda _{j-}^{1-} \\ \frac{\lambda _{j}^{2}-x}{\lambda _{j}^{2}-\lambda _{j}^{1}~} & x\in [\lambda _{j}^{1}, \lambda _{j}^{2}\text{ }\!\!]\!\!\text{ } \\ \end{array} \right.\text{ } $ | (1) |
| $ f_{j}^{s}\left( x \right)=\left\{ \begin{array}{*{35}{l}} \ \ \ \ \ 0 & x\notin \left[ \lambda _{j}^{s-1}, {{a}_{s+1}} \right] \\ \frac{x-\lambda _{j}^{s-1}~}{x_{j}^{s}-\lambda _{j}^{s-1}}~ & \ \ x\in [\lambda _{j}^{s-1}, \\ \ \ \ \ \ 1 & \ \ x\in [\lambda _{j}^{s}, {{a}_{s+1}}] \\ \end{array} \right. $ | (2) |
第四步:对于灰类k(k∈{2, 3, ……, s-1}),同时连接点(λjk,1)与灰类k-1的几何中点(λjs,0),得到j指标关于灰类k的三角可能度函数fjk[λjk-1,λjk,-,λjk+1],j=1,2,…,m,k=2,…,s-1。
对于指标j的一个观测值x,可由公式(3)计算出其属于灰类k的可能度值fjk(x)。
| $ f_{j}^{k}\left( x \right)=\left\{ \begin{array}{*{35}{l}} \ \ \ \ \ 0 & x\notin \left[ \lambda _{j}^{k-1}, \lambda _{j}^{k+1} \right] \\ \frac{x-\lambda _{j}^{k-1}~}{\lambda _{j}^{k}-\lambda _{j}^{k-1}}~ & \ \ x\in [\lambda _{j}^{k-1}, \lambda _{j}^{k}] \\ \frac{\lambda _{j}^{k+1}-x~}{\lambda _{j}^{k+1}-\lambda _{j}^{k}} & \ \ x\in [\lambda _{j}^{k}, \lambda _{j}^{k+1}] \\ \end{array} \right. $ | (3) |
第五步:确定各指标的权重ηj。
第六步:计算综合聚类系数σik,
绿色发展效应评价中共有30个三级指标,每个指标可以分为较差、一般、良好三个灰类,灰类序号k(k=1,2,3)。依据上述不同年份各项指标值,经过主观和客观的评价,确定各项指标关于不同灰类的取值范围。30个指标不同灰类的白化权函数如表 4所示。
|
|
表 4 白化权函数 |
根据上述模糊综合分析法的权重设定原则,进行本部分权重的确定工作。由一级指标权重乘上二级指标权重,再乘上三级指标权重,最终得到每一个三级指标的权重。如表 5所示。
|
|
表 5 三级指标权重 |
将2018年30个指标数据,各个指标三个灰类的可能度函数,以及不同指标的权重导入灰色建模软件中,可以得到2018年黄河三角洲滨海湿地绿色发展效应所处的三个灰类的聚类系数,结果如表 6所示。
|
|
表 6 聚类系数 |
根据max{σik}可以得出对象i所属灰类,由表 7数据可以看出,总体在σ3上数值最大,属于第三灰类,即2018年黄河三角洲滨海湿地绿色发展效应评价为良好。
|
|
表 7 黄河三角洲滨海湿地定基发展指数 |
综合两种评价方法,可以看出两种方法的结果是一致的:黄河三角洲湿地地区2018年度的绿色发展效应的评定等级均处在良好。这在一定程度上说明黄河三角洲湿地总体发展态势是良好的,在湿地的开发利用以及保护过程中,基本实现了绿色低碳循环发展。
五、滨海湿地绿色发展效应指数 (一) 各指标定基发展指数利用指标体系构建测度模型,本模型对指标体系中的正向指标、逆向指标等不同类型的指标,依照不同的处理方法计算其定基发展指数,用rik代表第i个指标第k年度的定基指数。
1、人均GDP的定基发展指数设置2012年人均地区生产总值为100的定基指数。记滨海湿地第i个指标的第k年的定基指数为rik(1≤i≤30,2012≤k≤2018),将其确定为各经济指标的基准定基发展指数,记为:
| $ {{A}_{1}}=~\frac{\text{max}\left( {{x}_{ik}} \right)}{~\text{min}\left( {{x}_{ik}} \right)}\text{ }\times ········100\% $ | (4) |
对于人均森林面积等正向指标,为消除量纲影响,使其标准化后与人均GDP定基可比,计算公式为:
| $ {{r}_{ik}}=100+\frac{{{x}_{ik}}-\text{min}\left( {{x}_{ik}} \right)}{\text{max}\left( {{x}_{ik}} \right)-\text{min}\left( {{x}_{ik}} \right)}\text{ }\!\!~\!\!\text{ }\times {{A}_{1}}\times 100\% $ | (5) |
其中,1≤i≤30,2012≤k≤2018,max(xik)为第i个指标2012-2018年中数据的最大值,min(xik)为第i个指标2012-2018年数据中的最小值。
3、逆向指标的定基发展指数逆向指标定基发展指数计算公式为:
| $ {{r}_{ik}}=100+\frac{\text{max}\left( {{x}_{ik}} \right)-{{x}_{ik}}}{\text{max}\left( {{x}_{ik}} \right)-\text{min}\left( {{x}_{ik}} \right)}\times {{A}_{1}}\times 100\% $ | (6) |
其中,1≤i≤30,2012≤k≤2018,max(xik)为第i个指标2012-2018年中数据的最大值,min(xik)为第i个指标2012-2018年数据中的最小值。
经计算得到滨海湿地2012—2018年各指标定基发展指数,即一个30×7阶的矩阵,如式(7)。
| $ r={{r}_{ik}}=\text{ }\left[ \begin{array}{*{35}{l}} {{r}_{1, 2018}} & {{r}_{1, 2017}} & \ldots & {{r}_{1, 2012}} \\ {{r}_{2, 2018}} & {{r}_{2, 2017}} & \ldots & {{r}_{2, 2012}} \\ \ \ \ \vdots & \ \ \ \vdots & \ \ \ \vdots & \ \ \ \vdots \\ {{r}_{30, 2018}} & ~{{r}_{30, 2017}} & \ldots & {{r}_{30, 2012}} \\ \end{array} \right]~ $ | (7) |
ηi是第i个指标的权重,2012—2018年滨海湿地高质量定基综合发展指数计算公式如式(8),R是用选定权重ηi与各指标定基发展指数加权计算后,形成的一个1×7阶的矩阵,其中权重的选取与灰色聚类的评估方法保持一致。
| $ \left[ {{R}_{2018}}~\ \ {{R}_{2017}}\ \ \cdots \ \ {{R}_{2012}} \right]~=\\ \text{ }\left[ {{\eta }_{1}}\ \ {{\eta }_{2}}\ \ \cdots \ \ {{\eta }_{30}} \right]\left[ \begin{array}{*{35}{l}} {{r}_{1, 2018}} & {{r}_{1, 2017}} & \ldots & {{r}_{1, 2012}} \\ {{r}_{2, 2018}} & {{r}_{2, 2017}} & \ldots & {{r}_{2, 2012}} \\ \ \ \ \vdots & \ \ \ \vdots & \ \ \ \vdots & \ \ \ \vdots \\ {{r}_{30, 2018}} & {{r}_{30, 2017}} & \ldots & {{r}_{30, 2012}} \\ \end{array} \right] $ | (8) |
根据上述测度模型,计算得到滨海湿地2012—2018年高质量定基综合发展指数,如表 7所示。从测度结果看,2012—2018年,滨海湿地各指标定基发展质素呈现上升趋势,滨海湿地的发展趋好。
据此,计算滨海湿地2012-2018年高质量定基综合发展指数为:
| $ \begin{align} & \left[ {{R}_{2018}}~\ \ {{R}_{2017}}\ \ ~\ldots \text{ }\ \ {{R}_{2012}}~ \right] =\\ & \left[ 101.0739\ \ 100.9875\ \ 100.7865\ \ 100.7494\ \ 100.7155\ \ 100.4329\ \ 100.4617 \right] \\ \end{align} $ | (9) |
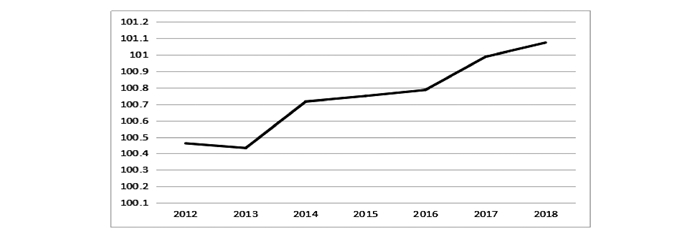
各指数的数值及变化趋势可以由图 1来表示。
|
图 1 2012-2018年高质量定基综合发展指数变化趋势 |
由滨海湿地2012—2018年高质量定基综合发展指数的变化可知,黄河三角洲的湿地绿色发展指数在2013年有小幅度的下降,从2013—2018年绿色发展指数稳步上升,呈现越来越好的趋势。所以伴随着东营市经济社会的不断发展,环境问题日益凸显,政府等相关部门开始加强环境保护的管理。此外,近年来党和国家也提出绿色发展等生态理念,绿水青山就是金山银山的环保意识成为各级政府的关注焦点,一系列的政策与措施促使东营市滨海湿地绿色发展保持良好的发展势头。
六、结论与政策建议 (一) 主要结论本文主要以黄河三角洲滨海湿地为研究对象,综合运用了模糊评价法与灰色聚类评估方法对该湿地的绿色发展效应进行测度,研究结果显示,黄河三角洲2018年的绿色发展效应的评价等价均为良好。在此基础之上,文章又测算了滨海湿地2012年到2018年绿色发展效应指数,结果显示黄河三角洲滨海湿地的绿色发展综合指数一直处于上升态势。
因此,根据实证分析结果得出,黄河三角洲湿地在2012年到2015年期间发展状况较为乐观,基本满足低碳循环的绿色发展要求。由此说明政府等相关部门加大了对滨海湿地的保护以及科学管理力度,在国家大力提倡环境保护的背景下,黄河三角洲滨海湿地已初步实现了绿色、低碳、循环的可持续发展目标。
(二) 政策建议第一,协调好经济发展与滨海湿地保护间的关系,贯彻科学绿色发展观。对于滨海湿地,政府要统筹协调好发展农业、开采资源等经济活动与湿地的可持续发展之间的关系,做到“地上与地下兼顾,综合开发,统筹管理”,实现经济效益、社会效益和生态效益的统一。应调整产业结构,大力发展生态经济。结合湿地生态园区和光合湿地水产品示范区建设,进行科技示范区建设和管理。在保护湿地生态环境的同时提高当地的经济发展水平,提高第三产业在GDP中的占比。
第二,制定滨海湿地绿色发展法规。规范湿地的开发和利用程序,“实行最严格生态环境保护制度”的严密法治观。制定湿地开发管理的统一法规,进行统一的规划协调。确保保护区内的一切资源由保护区机构统一管理。保护区范围内的开发和建设服从保护区的发展规划,依据规划按核心区、缓冲区和实验区分区利用。发挥立法在滨海湿地保护中的根本作用,使滨海湿地的保护和管理逐步走上法制化轨道。
第三,实施滨海湿地生态环境管理和生态系统恢复调整。通过合理替代途径进行补偿,用于补偿的生态系统与原有生态系统具备结构与功能上的等同性,是在空间维上寻求协调保护和开发的途径,关键是提高科研水平,运用保护生态学和恢复生态学的理论加强湿地的保护和恢复。
| [1] |
Hong S, Kim S, Kim J. Implications of potential green tourism development[J]. Annals of Tourism Research, 2003, 30(2): 323-341.
(  0) 0) |
| [2] |
Marco-Fondevila Miguel, Moneva Abadía, José M, Scarpellini Sabina. CSR and green economy: Determinants and correlation of firms'sustainable development[J]. Corporate Social Responsibility & Environmental Management, 2018, 25(05): 756-771.
(  0) 0) |
| [3] |
Luukkanen J, Kaivo-oja J, Vahakari N, O'Mahony T, Korkeakoski M, Panula-Ontto J, Phonhalath K, Nanthavong K, Reincke K, Vehmas J, Hogarth N. Green economic development in Lao PDR: A sustainability window analysis of Green Growth Productivity and the Efficiency Gap[J]. Journal of Cleaner Production, 2019, 211: 818-829. DOI:10.1016/j.jclepro.2018.11.149
(  0) 0) |
| [4] |
杜永强, 王悦, 李晶洁, 等. 基于主成分分析的经济绿色发展评价研究[J]. 科技和产业, 2018, 18(10): 50-59. DOI:10.3969/j.issn.1671-1807.2018.10.011 (  0) 0) |
| [5] |
朱芬华. 绿色发展理念视域下经济发展与资源环境耦合协调发展的实证研究[J]. 安徽商贸职业技术学院学报(社会科学版), 2018, 17(1): 7-11. (  0) 0) |
| [6] |
王海军, 邹日崧. 国外绿色经济典型城市发展经验比较及启示[J]. 沈阳工业大学学报(社会科学版), 2019, 17(3): 1-8. (  0) 0) |
| [7] |
K Ermis, A Midilli I Dincer, M A Rosen. Aritificial neutral network analysis of world green energy use[J]. Enengy Policy, 2007, 35: 1731-1743. DOI:10.1016/j.enpol.2006.04.015
(  0) 0) |
| [8] |
Makridou G, Andriosopoulos K, Doumpos M. Measuring the efficiency of energy-intensive industries across European countries[J]. Energy Policy, 2016, 88(1): 573-583.
(  0) 0) |
| [9] |
李春友, 何广銮. 绿色发展视角下矿产资源利用绩效评价——以X矿产企业为例[J]. 纳税, 2018, (16): 154-157. (  0) 0) |
| [10] |
聂弯. 资源环境约束下培育绿色发展新动能战略路径研究——以大庆市为例[J]. 生态经济, 2018, 34(5): 66-69. (  0) 0) |
| [11] |
James G Titus. Greenhouse effect and coastal wetland policy: How Americans could abandon an area the size of Massachusetts at minimum cost[J]. Environmental Management, 1991, (1).
(  0) 0) |
| [12] |
Osland Michael J, Gabler Christopher A, Grace James B, Day Richard H, McCoy Meagan L, McLeod Jennie L, From Andrew S, Enwright Nicholas M, Feher Laura C, Stagg Camille L, Hartley, Stephen B. Climate and plant controls on soil organic matter in coastal wetlands[J]. Global Change Biology, 2018, 24(11): 5361-5379. DOI:10.1111/gcb.14376
(  0) 0) |
| [13] |
王爱军, 陈坚. 厦门滨海湿地退化机制及可持续发展[J]. 海洋开发与管理, 2006, (6): 184-186. DOI:10.3969/j.issn.1005-9857.2006.06.052 (  0) 0) |
| [14] |
许国晶, 李秀启, 客涵. 基于能值分析的黄河口滨海湿地生态价值评价[J]. 中国农学通报, 2013, 29(35): 211-217. DOI:10.11924/j.issn.1000-6850.2013-1857 (  0) 0) |
| [15] |
王迪, 李团结, 谢敬谦. 广东省海岛(岛礁)滨海湿地现状与保护[J]. 湿地科学与管理, 2018, 14(3): 34-37. DOI:10.3969/j.issn.1673-3290.2018.03.08 (  0) 0) |
| [16] |
徐建国, 郑国建, 孔维健. 南四湖生态湿地产业发展模式[J]. 湿地科学与管理, 2013, 9(1): 45-48. DOI:10.3969/j.issn.1673-3290.2013.01.12 (  0) 0) |
| [17] |
刘玉安, 段炼, 解鹏飞, 等. 大连市滨海湿地现状及加强管护工作对策研究[J]. 海洋开发与管理, 2017, 34(11): 54-60. DOI:10.3969/j.issn.1005-9857.2017.11.011 (  0) 0) |
| [18] |
Virginia D Engle. Estimating the Provision of Ecosystem Services by Gulf of Mexico Coastal Wetlands[J]. Wetlands, 2011, (31): 179-193.
(  0) 0) |
| [19] |
Simpson L T, Osborne T Z, Duckett L J, Feller I C. Carbon Storages along a Climate Induced Coastal Wetland Gradient[J]. Wetlands, 2017, 37(06): 1023-1035. DOI:10.1007/s13157-017-0937-x
(  0) 0) |
| [20] |
丁冬静, 廖宝文, 管伟, 等. 东寨港红树林自然保护区滨海湿地生态系统服务价值评估[J]. 生态科学, 2016, 35(6): 182-190. (  0) 0) |
| [21] |
李楠, 李龙伟, 张银龙, 等. 杭州湾滨海湿地生态系统服务价值变化[J]. 浙江农林大学学报, 2019, 36(1): 118-129. (  0) 0) |
| [22] |
李晓西, 潘建成. 中国绿色发展指数的编制——《2010中国绿色发展指数年度报告——省际比较》内容简述[J]. 经济研究参考, 2011, (2): 36-64. (  0) 0) |
 2019
2019 
