肾综合征出血热（hemorrhagic fever with renal syndrome，HFRS）又称流行性出血热，是由汉坦病毒引起的，以鼠类为主要传染源的自然疫源性疾病，包括流行性出血热（主要分布在亚洲）和流行性肾病（主要分布在欧洲）。据报道，中国大陆地区年发病数为4～6万，具有季节特征，每年均有不同程度的流行，且新疫区和转型疫区不断出现^[1]。为此，了解HFRS的发病趋势和季节性，建立预测模型，有助于在疫情暴发前采取预防控制措施，降低其流行强度和发病率。一般对于HFRS疫情的研究多局限在某一地区，通常以年或月发病率进行预测^{[2 – 3]}，而描述全国的流行趋势以及基于剔除季节因素的非季节性数据进行预测的研究并不多见。时间序列分解法适用于季节性较强的、一次性短期预测或在使用其他预测方法前消除季节变动因素的影响^[4]。因此，本研究基于时间序列分解法研究中国2011 — 2016年HFRS的发病趋势和季节性，建立预测模型并评价其效果。结果报告如下。

HFRS发病资料来源于国家卫生部网站（http://www.moh.gov.cn）2011年1月1日 —2016年12月31日逐月报告的发病数。

采用Excel 2007处理数据，应用R 3.4.0软件进行统计分析。（1）数据预处理：统计全国2011年1月1日 — 2016年12月31日每月报告的HFRS原始发病数N_i。按照国家统计局公布的2011 — 2016年年均人口自然增长率（分别为4.79 ‰、4.95 ‰、4.92 ‰、5.21 ‰、4.96 ‰、5.86 ‰），以各月天数和人口月平均增长率校正发病数，校正后的发病例数记为X_i^[5]。（2）时间序列分解法：时间序列一般包括长期趋势（T）、季节变动（S）、周期变化（C）和不规则变动（I）四类因素，Y_t = f （T_t, S_t, C_t, I_t）^{[4, 6]}。常用模型有乘法模型和加法模型。乘法模型假定各因素相互影响，用于相对数总变动的计算；加法模型假定各因素相互独立，用于总量指标总变动的计算^[7]。本研究采用乘法模型进行时间序列的分解，公式为： $\mathop Y\nolimits_t = \mathop T\nolimits_t \times \mathop S\nolimits_t \times \mathop C\nolimits_t \times \mathop I\nolimits_t $ 。（3）季节指数分解：使用跨度等于周期加1并以 0.5 加权的端点计算移动平均数，一定程度上抵消随机性和季节性的正负波动^[8]，移动平均数序列（T × C）只含长期趋势和周期变动因素。将校正病例数除以（T × C），剔除长期趋势和周期变动因素，得到只含季节因素和不规则变动因素的序列（S × I）。公式为： $\displaystyle\frac{{\mathop X\nolimits_i }}{{T \times C}} =$ $\displaystyle\frac{{T \times S \times C \times I}}{{T \times C}} = S \times I$ 。取各年同一月（S × I）均值S₁，去掉不规则变动的影响并进行调整，即为各月季节指数S₂ ，公式为： $\mathop S\nolimits_2 = \frac{{12}}{{\sum {\mathop S\nolimits_1 } }} \times \mathop S\nolimits_1 $ ^[7]。（4）非季节性处理：校正病例数（Xi）除以季节指数（S₂），剔除季节性因素，为不含季节变动的非季节性数据，公式为： $\mathop {X'}\nolimits_i = \mathop X\nolimits_i /\mathop S\nolimits_2 = T \times C \times I$ 。（5）建立预测模型^[9]：通过数据变换或差分使序列满足平稳性假定，利用单位根（augmented Dickey-Fuller，ADF）检验来验证。根据平稳序列的自相关函数（auto correlation function plot，ACF）图和偏自相关函数（partial autocorrelation function plot，PACF）图选定参数，拟合模型，通过对模型的系数和残差进行检验，判断模型的适合性。建立HFRS月发病数的预测公式： $\mathop Y\nolimits_i = \mathop {X'}\nolimits_i \times \mathop S\nolimits_2 $ 。（6）评价模型预测精度：以2011—2016年HFRS月发病数进行回代检验，计算平均绝对误差（mean absolute error，MAE）、均方根误差（root mean square error，RMSE）和平均绝对百分误差（mean absolute percentage error，MAPE）评价模型预测精度。

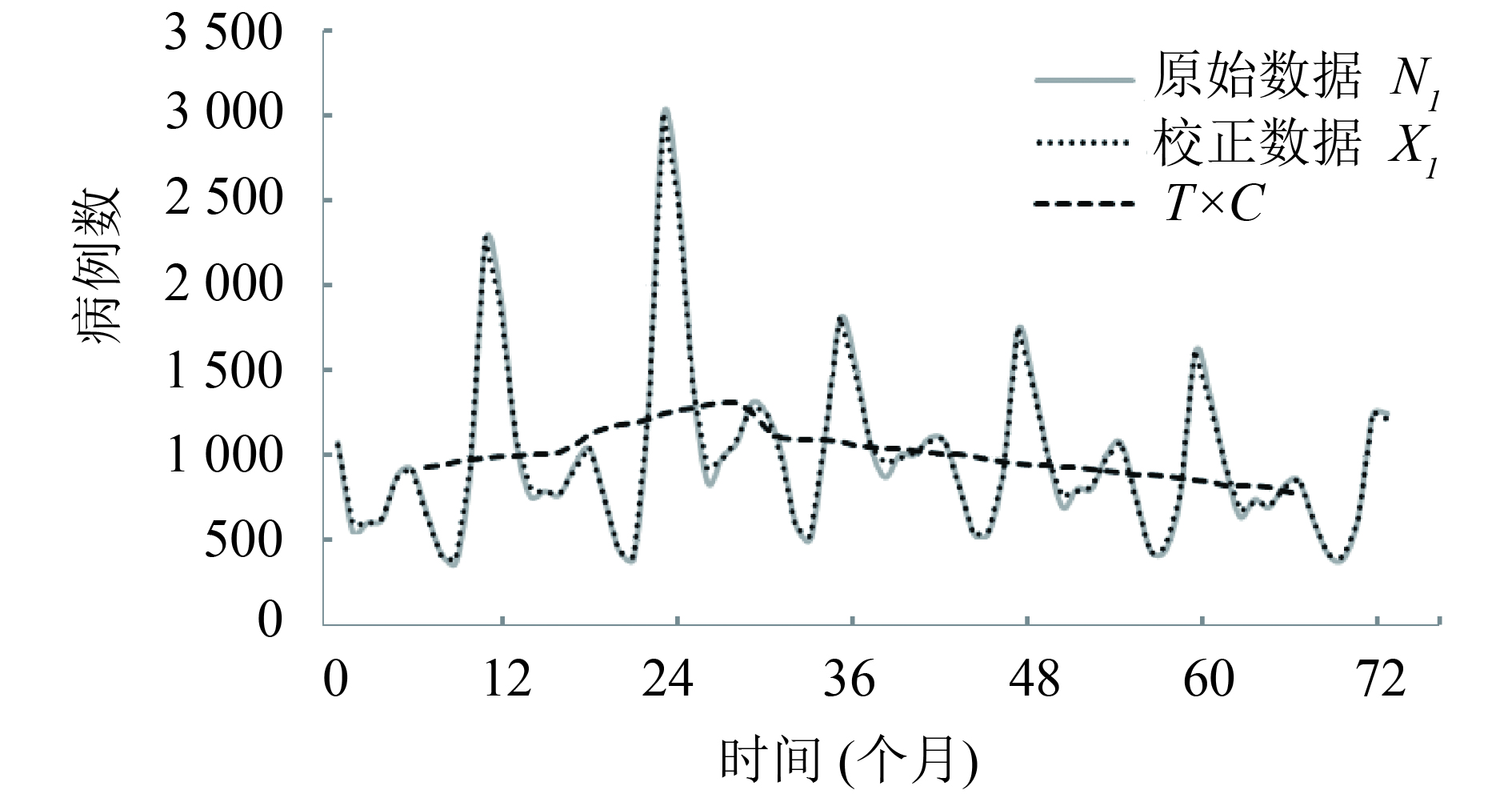
中国2011 — 2016年报告HFRS平均月发病数987例，校正后983例。图1显示校正后的数据变化不大，但更平稳，不再有小波动。2011 — 2012年发病呈上升趋势，2013年发病数达到高峰，此后迅速下降并保持平稳，略有缓慢降低的趋势。一年四季均有病例出现，疫情呈周期性和季节性波动。（T × C）趋势图表明全国HFRS病例数在2011年中期至2013年初期呈上升趋势，其后不断下降。

图 1

图 1 中国2011 — 2016年HFRS月发病原始和校正病例数及（T × C）序列图

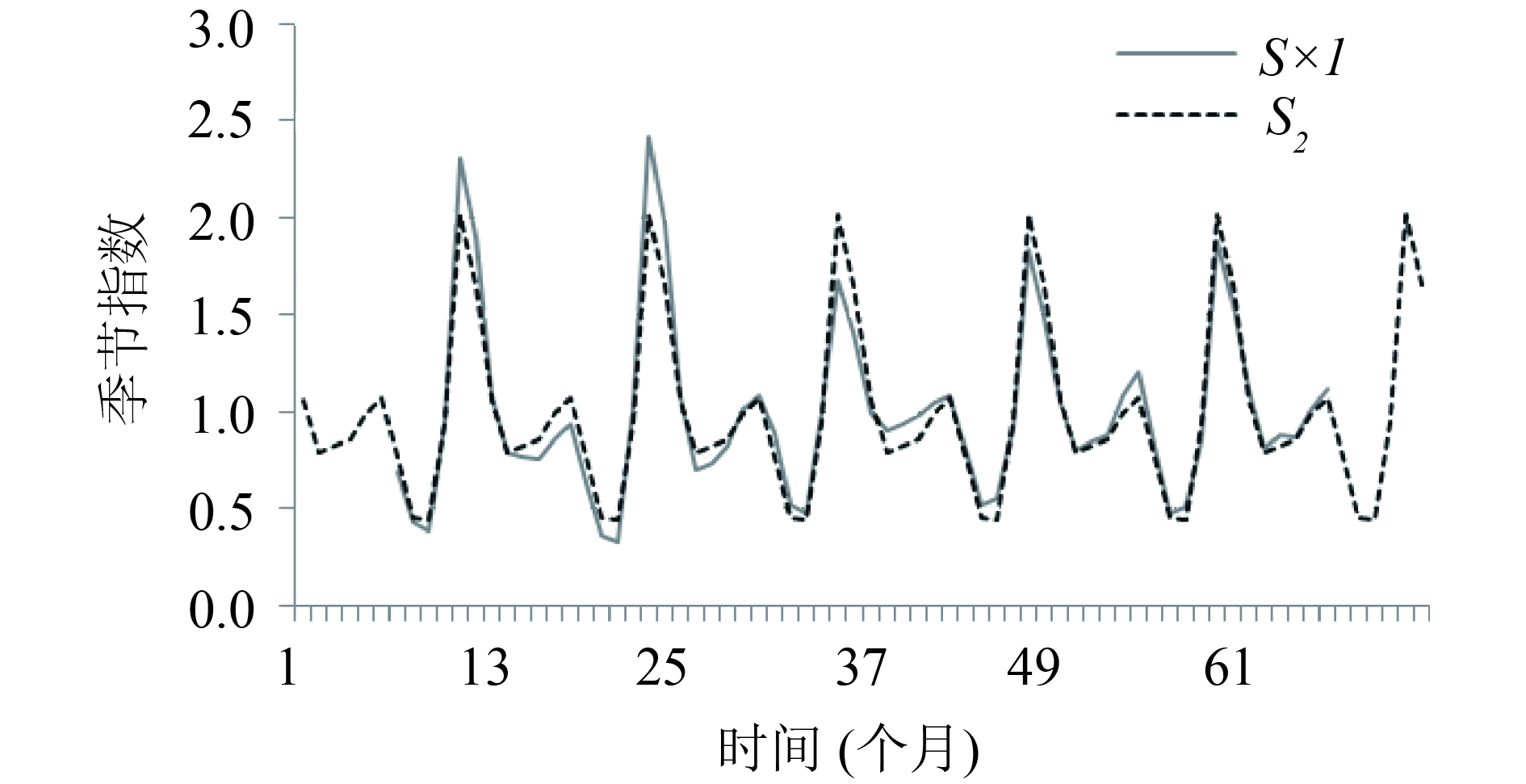
季节指数S₁之和为12.833，按公式进行调整后的S₂值在5、6、11、12月和次年1月均 > 1，分别为1.066、1.007、1.084、2.024和1.666。图2显示HFRS发病数季节特征明显，呈双峰型。第1个发病高峰多在5 — 6月，第2个出现在11月 — 次年1月，且疫情重于前一个高峰。2个低谷期分别在每年2月和8 — 9月。

图 2

图 2 季节指数图

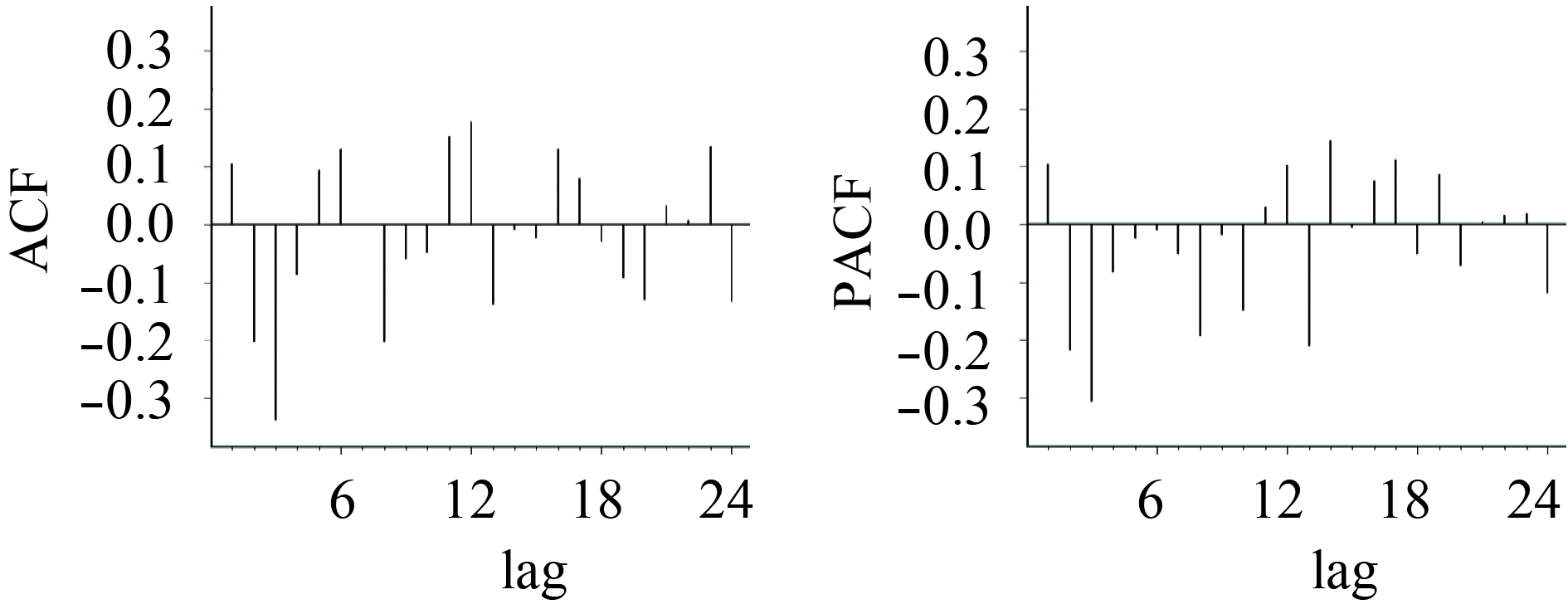
非季节性数据（X’_i）一次差分后，单位根检验的P < 0.01，满足平稳性假定。一次差分后的ACF和PACF均截尾，识别为差分自回归移动平均模型ARIMA，且 d = 1，根据滞后项（lag），考虑p和q最大取2，在模型通过假设检验的前提下，依据赤池信息（Akaike information criterion，AIC）准则，确定最优模型为ARIMA （2, 1, 1）。

图 3

图 3 X’i序列一次差分后的ACF图和PACF图

模型统计量log likelihood =– 429.2，AIC = 866.4，BIC = 875.45，自回归（autoregression, AR）和移动平均（moving average, MA）的系数（B）及假设检验见表1。

表 1

表 1 ARIMA（2, 1, 1）模型的参数估计与检验 参数 B $ {S_{\overline x}}$ t 值 P 值 AR 1 0.786 7 0.164 9 4.770 8 < 0.001 AR 2 – 0.354 3 0.119 9 – 2.955 0 < 0.010 MA – 0.744 1 0.141 1 – 5.273 6 < 0.001

表 1 ARIMA（2, 1, 1）模型的参数估计与检验

残差序列Ljung-box检验的统计量Q（20）= 16.364，P = 0.694，残差不存在自相关，为白噪声序列，模型可较好的拟合该数据。最终预测公式为Y_i = ARIMA （2, 1, 1） × S₂。

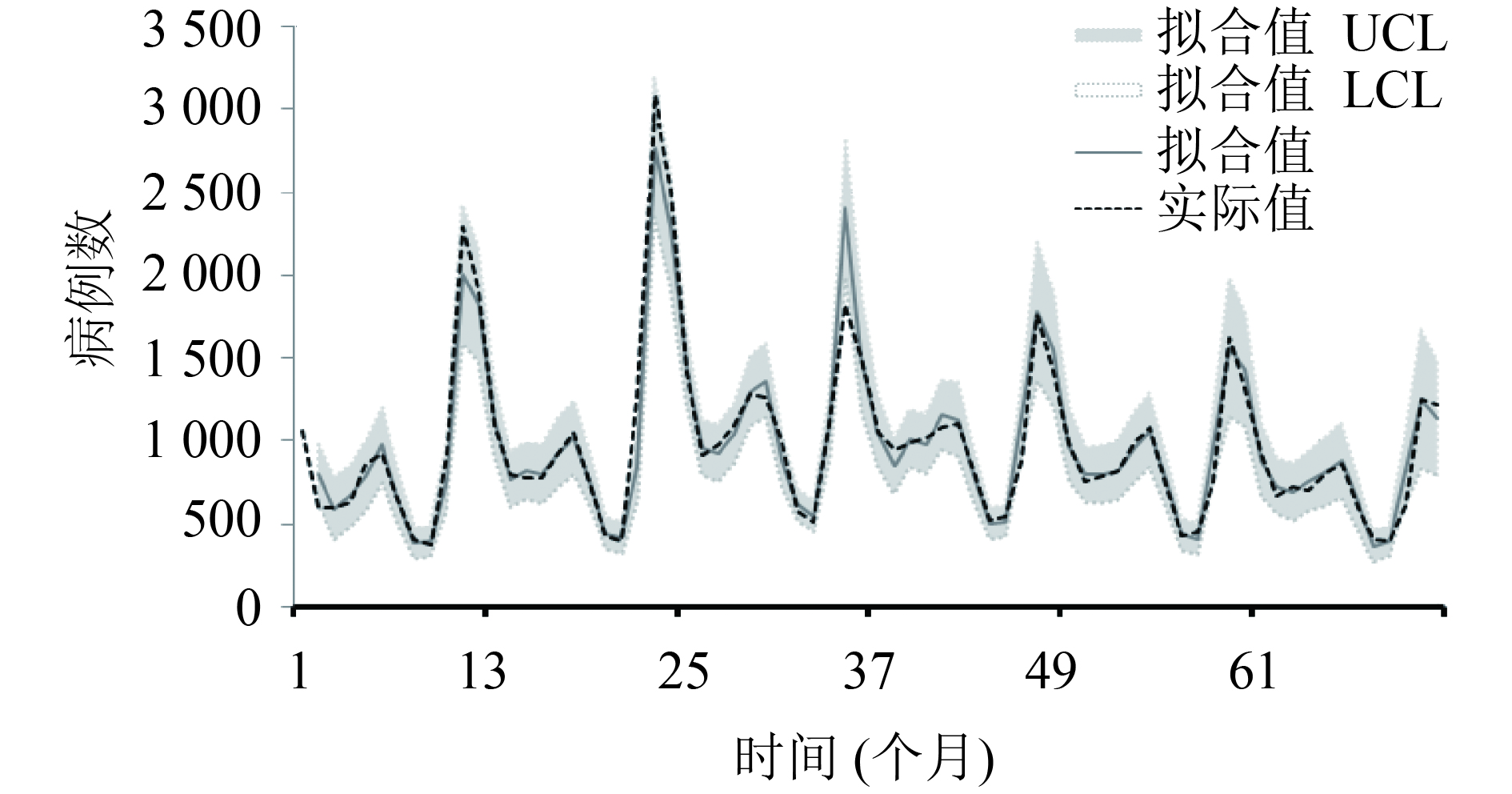
ARIMA（2, 1, 1）模型的MAE、RMSE和MAPE分别为66.54、101.05和6.83 %。建立HFRS月发病数的预测模型，以2011 — 2016年HFRS月发病数进行组内回代检验，MAE、RMSE和MAPE分别为71.31、122.43和7.00 %。图4显示了拟合值、95 % CI的上限（upper confidence limit ，UCL）、下限 （lower confidence limit ，LCL）和实际值的序列图，实际值均落在95 % CI内。

图 4

图 4 中国2011 — 2016年HFRS月发病数的实际值和拟合值

时间序列分解法不考虑外部影响因素，最大限度地利用时间序列分解出疾病的趋势和季节性变动因素，以序列图的形式直观地展示出发病趋势和季节特征。本研究采用时间序列分解法研究中国2011 — 2016年HFRS的发病趋势，结果显示在2011年中期至2013年初期发病上升，其后缓慢下降。全国HFRS发病数统计结果显示，2011 — 2013年初发病人数增加，2013年中期至2015年初期的发病数下降^[10]。总体来看，HFRS发病表现出上升到下降的波动状态。HFRS的防控取得了一定成效，疫情有所缓解，但影响其发病的环境因素存在不确定性，有疫情反复的可能，有关部门需重视预防措施和监测工作，保持环境卫生，提高易感人群疫苗接种率，将发病数控制在较低水平。

季节指数S₂ > 1，说明季节性大于平均值，出现流行高峰。（ S × I）指标结合了季节性和不规则变动因素，两者差值越大，说明随机性对季节性的影响越大，综合考虑（S × I）和S₂可以更准确地研究疾病季节性。（S × I）和S₂曲线趋势基本一致，前2年（S × I）曲线波动较大，随机性因素对发病的影响较大。HFRS发病季节特征显著，5 — 6月和11月 — 次年1月均为发病高峰。研究表明，姬鼠型HFRS发病高峰季节在秋冬之间（10 — 12月），家鼠型HFRS则在春夏之间（3 — 6月）^[1]。建议政府部门应密切关注随机或突发因素对发病的影响，在高发季节前加强疫情监测，组织开展防鼠灭鼠和卫生宣传教育工作。

时间序列预测是根据历史数据随时间的变化规律建立的数学模型，短期预测精度较高^[11]。ARIMA模型适用于流行因素较稳定疾病的预测，特别是季节性明显的传染病^[12]，因此被广泛用于传染病预测^[13]。HFRS发病季节特征明显，在以发病率拟合预测模型时，需要考虑时间序列的季节性^[14]。本研究采用时间序列分解法分解出非季节性数据，作为时间序列来拟合ARIMA模型，结合季节指数建立HFRS月发病数预测模型ARIMA（2, 1, 1）× S₂ ，较准确地拟合了2011 — 2016年HFRS月发病数，表明该方法适用于HFRS月发病数的预测。梅树江等^[15]建立预测模型ARIMA（1, 0, 1）（1, 0, 1）₁₂对广东省深圳市2014年HFRS发病率预测的相对误差为20.74 %；Wang等^[16]以山东省淄博市2004 — 2011年HFRS发病率建立的预测模型预测2014年发病率的MAPE为11.5 %。一般认为MAPE < 10 %～15 %时预测精度较好，本研究的MAPE为7.00 %，提示以非季节性数据结合季节指数进行预测有较高的精度。由于非季节性数据是剔除了季节变动因素的，因此在拟合ARIMA模型时无需考虑季节特征，需要的参数较少，模型相对简单，可达到较高的预测精度。

由于无法获得统计指标证明显著性是时间序列分解法的一大局限性，因此在判断季节特征、高峰期月份时带有主观因素，而本研究基于时间序列分解法建立的模型则能较好预测HFRS的月发病数。但本研究以全国发病数为基础，因而忽略了不同地区气候地理差异和社会环境因素，也未考虑到HFRS发病的动物宿主、疫源地迁移、经济变化等其他影响因素，因此在以后的研究中应缩小研究区域，综合考虑当地的气候环境因素，以便更准确地估计HFRS的发病情况。