手足口病是一种常见的丙类传染病[1],可用一般的数据模型进行暴发预警[2]。暴发预警以监测数据为基础,根据传染病预警中常用模型设置基线和预警阈值,如当前期监测数据偏离基线并超过了阈值,则发出预警[3-4]。考虑到各模型对不同疾病、不同地区的预警功效有差异,且真实环境中往往缺少足够的疫情暴发事件来测试模型预警功效,本研究以湖北省潜江市2013年4月1日—2014年3月31日的手足口病数据为基础,利用模拟暴发来探索不同时间预警模型在当地手足口病预警中的功效,优选各模型的预警阈值并综合评价其预警效能,为自动预警技术提供理论支持。
1 资料与方法 1.1 资料来源数据来源于湖北省潜江市疾病预防控制中心的中国疾病预防控制系统,选取全市2013年4月1日—2014年12月31日报告的手足口病日发病数作为背景数据进行分析。
1.2 模型及参数设置 1.2.1 Shewhart控制图模型在传染病预警中,若监测病例数Xi超过上控制线(upper control limit,UCL)则该模型发出预警信号。UCL计算公式如下:UCL=x+k×s。式中,x、s为所用基线数据的均值和标准差,k为置信系数。本研究中k取0.5~5.0,间隔为0.5。
1.2.2 移动平均(moving average, MA)设原有时间序列yn,MA模型定义距离当前期最近的k天(包括当前日)内的日病发病均值μk为“当前期监测值”,并与预期值μi比较。MA模型统计量为Mt=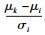
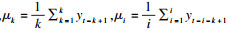
根据历史数据距当前值的时间远近赋予相应权重以估算当前值,即在时间序列yn中,估计(t+1)期的预期数为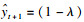
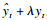
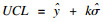
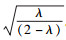
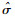
假定监测数据服从Poisson分布[5],将每日监测病例数作标准化正态处理,得到的标准正态离差表示监测值与预期值的差异: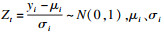
(1) EARS′C1模型假定时间序列yn服从正态分布,将最近7 d的监测数据作为基线数据,模型统计量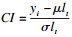
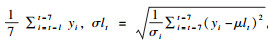
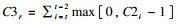
设定模拟暴发服从Poisson分布,以一次暴发时总人数中发病人数的占比作为暴发强度(intense),设定强度分别为0.2、0.5和0.8。设暴发持续时间(duration)分别为3、7、14 d。计算每日病例数均值。对于每个服从Poisson分布的模拟暴发,其参数仅与λ相关,公式如下:λ=x×intense×duration。参考文献[8]并利用Excel 2013合成模拟暴发数据。
1.3.2 暴发的插入及运行将背景数据的前1周数据作为基线以便于各预警模型计算初始均值以及标准差,从背景数据的第8 d作为手足口病疫情暴发的起始日开始插入模拟暴发,将同日背景数值与暴发相应数值相加即为模拟监测值。每一次插入暴发均可得到该次模拟暴发后利用某一模型监测的相关指标,如正确预警暴发数、插入暴发数、正确预警信号数等。计算结束后清空该次暴发种子的插入,在后1日继续插入同一暴发种子并重复上述计算过程。按上述方法逐日插入暴发种子可得结果后,同一类型的评价指标再求均值得到最终的灵敏度和特异度。
1.4 评价指标和方法综合考虑灵敏度、特异度、约登指数、受试者工作曲线(receiver operating characteristic curve,ROC)、动态监测工作特征曲线(acitve monitoring operation curve,AMOC)和检出时间(detection time,DT)来寻找最优模型。其中,在每次模拟暴发插入后,能在暴发持续时间内监测到暴发并发出预警,记录暴发1、插入暴发数1;若未能探测到暴发则记录暴发0,插入暴发数1。在插入的总暴发数中共探测到暴发数所占的比值,即为该模型的灵敏度。公式为:


模拟暴发的插入和运行均利用Excel 2013中加载的VBA程序对各模型编程,随后进行相应的计算。
2 结果 2.1 流行病学特征及各模型的ROC曲线和AMOC曲线比较2013年4月1日—2014年12月31日潜江市共上报手足口病1 841例, 4—6月、11月—次年1月的存在发病高峰。其中散居儿童占76.81%(1 412/1 841),幼托儿童21.51%(396/1 841),以散发为主。男性患者1 206例,女性患者635例,性别比1.9:1;年龄分布在1个月~27岁,以0~4岁为比例最高,达到总数的95.44%。对于潜江地区的手足口病的预警,各模型的ROC曲线和AMOC曲线相似,灵敏度提高则特异度下降,特异度升高的则DT增加,总的功效相差不大。
2.2 各模型最佳预警阈值下的功效比较(表 1)| 表 1 手足口病不同预警模型的最佳功效a |
所比较的结果来源于9种暴发形态下的平均结果。通过设置预警阈值h为0.5~5.0的比较发现,各模型均在h=0.5时取得最佳预警效果。各模型的约登指数相差不大,其中Shewhart模型的灵敏度最高,DT最短;而CUSUM模型的特异度较高。其中,Shewhart模型的约登指数为0.57,同时DT为1.12 d,在所有模型中相对功效最佳;而EWMA模型的约登指数最低为0.44,DT最长为3.70 d,功效较差。
2.3 不同模拟暴发数据的功效比较(表 2)| 表 2 不同模拟暴发数据的功效比较 |
通过分别对模拟暴发数据的单一影响因素进行分析发现,模拟暴发数据的不同,对各预警模型的功效均产生影响,主要表现在灵敏度和DT的变化,但对特异度的影响较小。暴发的强度越大,各模型的灵敏度越高,DT越短;而暴发的持续时间越长,灵敏度越高,而DT延长,但此时DT延长可能与模拟暴发数据本身的长度增长有关。
3 讨论目前在各种对预警模型的研究中,已经越来越广泛地通过模拟暴发的方式来评价模型的预警效果[11-12],但通过模拟暴发来评价多种预警模型在手足口病上的应用功效仍很少见。由于模拟暴发是人为加入的,形状、强度、持续时间这些参数可灵活的变化并可重复测试运算,在原始数据并未出现暴发也不会影响对于不同的预警方法之间的比较。在本研究中可以看到,基于模拟暴发数据的预警性能评价方法在潜江地区的手足口病的可适模型的研究中是切实可行的,该方法可定量地评估各预警模型预警能力的理论值,为潜江市的手足口病预警相关系统实现自动预警提供了理论支持,也为其他类似的研究提供一定参考依据。
本研究中各模型均有预警价值。在各种模型的对比中,Shewhart控制图模型在预警阈值0.5时取得最佳预警功效,此时模型的灵敏度和特异度分别为88.64%、68.20%,DT为1.12 d。虽然将预警阈值减小后,能使模型的功效增大,但考虑到阈值太低时预警失去实际意义,且加重了警报发出后因采取相应措施所需要的各种人力、物力及财力资源等负担,故不推荐采用。在实际应用过程中,预警模型和预警阈值的选择需根据不同的预警目的和要求进行调整和确定。在维持灵敏度不变的情况下,如要提高监测结果的特异性,还可考虑采用联合使用多种时间预警模型同时进行预警的方法来达到要求。
预警模型在医疗机构的监测系统早期预警中均有广泛应用[13-14],且在应用中预警效能均较好。但这些研究并未应用模拟暴发数据,仅对真实监测数据进行分析处理,可能与本研究存在一些不同。本研究中的预警模型效能仍有提高的可能,主要存在以下不足:首先,本研究中模拟暴发的形状设置为Poisson分布,但国内外其他研究中有将模拟暴发假定服从正态分布[8]、对数正态分布[15]或负二项分布[16]。随着模拟暴发事件的强度和持续时间变化,各模型的功效均会发生较明显的改变,故而选择合适参数的暴发事件来插入到背景数据中更有利于优选出功效高的预警模型。叶楚楚等[17]认为基于真实暴发病例进行的模拟比人为设置参数进行的模拟更科学且贴近实际。同时,加大模拟暴发数据量有利于更好的测试评价预警模型的功效。其次,本研究的背景数据存在季节性的较大高峰,其中有可能包含暴发事件,王小莉等[12]通过消峰对原始数据进行平滑处理发现可提高模型的敏感性。再次,本研究中各模型中均采用7 d的基线数据,可能会出现因基线数据少而导致预警指标不稳定的情况,周鼎伦等[18]的研究建议可适当延长基线时间改进模型的稳定性。
| [1] | Zhang Y, Zhu Z, Yang W, et al. An emerging recombinant human enterovirus 71 responsible for the 2008 outbreak of hand foot and mouth disease in Fuyang city of China[J]. Virol J, 2010, 7: 94. DOI:10.1186/1743-422X-7-94 |
| [2] | Unkel S, Farrington CP, Garthwaite PH, et al. Statistical methods for the prospective detection of infectious disease outbreaks:a review[J]. Journal of the Royal Statistical Society:Series A (Statistics in Society), 2012, 175(1): 49–82. DOI:10.1111/rssa.2011.175.issue-1 |
| [3] | 任赟静, 黄建始, 马少俊, 等. 症状监测及其在应对突发公共卫生事件中的作用[J]. 中华预防医学杂志, 2005, 39(1): 57–59. |
| [4] | 代小秋, 刘民. 症状监测预警系统中常用的统计学方法及其比较[J]. 中国卫生统计, 2011, 28(2): 221–224. |
| [5] | 宋姝娟, 丁华, 黄春萍, 等. 泊松分布在手足口病预警中的应用[J]. 浙江预防医学, 2015, 27(1): 32–35. |
| [6] | 刘文东, 胡建利, 艾静, 等. CUSUM模型在流行性腮腺炎早期预警中的应用研究[J]. 中国卫生统计, 2014, 31(4): 563–566. |
| [7] | Fricker RD, Hegler BL, Dunfee DA. Comparing syndromic surveillance detection methods:EARS' versus a CUSUM-based methodology[J]. Stat Med, 2008, 27(17): 3407–3429. DOI:10.1002/sim.v27:17 |
| [8] | Jackson ML, Baer A, Painter I, et al. A simulation study comparing aberration detection algorithms for syndromic surveillance[J]. BMC Med Inform Decis Mak, 2007, 7: 6. DOI:10.1186/1472-6947-7-6 |
| [9] | Hutwagner L, Browne T, Seeman GM, et al. Comparing aberration detection methods with simulated data[J]. Emerg Infect Dis, 2005, 11(2): 314–316. DOI:10.3201/eid1102.040587 |
| [10] | 程丽薇. 湖北省农村地区药物销售量监测系统应用研究[D]. 武汉: 华中科技大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10487-1014025123.htm |
| [11] | Buckeridge DL, Burkom H, Moore A, et al. Evaluation of syndromic surveillance systems-design of an epidemic simulation model[J]. MMWR Suppl, 2004, 53: 137–143. |
| [12] | 王小莉, 王全意, 刘东磊, 等. 采用北京市麻疹的暴发模拟数据比较几种预警模型的功效[J]. 中华流行病学杂志, 2009, 30(2): 159–162. |
| [13] | Monto AS, Comanor L, Shay DK, et al. Epidemiology of pandemic influenza:use of surveillance and modeling for pandemic preparedness[J]. J Infect Dis, 2006, 194(Suppl 2): S92–97. |
| [14] | Fan Y, Yang M, Jiang H, et al. Estimating the effectiveness of early control measures through school absenteeism surveillance in observed outbreaks at rural schools in Hubei, China[J]. PLoS One, 2014, 9(9): e106856. DOI:10.1371/journal.pone.0106856 |
| [15] | Miller B, Kassenborg H, Dunsmuir W, et al. Syndromic surveillance for influenza like illness in ambulatory care setting[J]. Emerg Infect Dis, 2004, 10(10): 1806–1811. DOI:10.3201/eid1010.030789 |
| [16] | 韩新焕. 负二项分布的性质特征及在流行病学研究中的应用[J]. 数理医药学杂志, 2009, 22(2): 138–140. |
| [17] | 叶楚楚. 大型活动症状监测预警方法研究[D]. 北京: 中国疾病预防控制中心, 2011. http://cdmd.cnki.com.cn/Article/CDMD-84501-1011210902.htm |
| [18] | 周鼎伦, 杨维中, 兰亚佳, 等. 暴发规模和持续时间对CUSUM预警模型效能的影响[J]. 中华流行病学杂志, 2012, 33(6): 617–621. |
 2017, Vol. 33
2017, Vol. 33


