2. 中国疾病预防控制中心性病艾滋病预防控制中心
多水平统计模型是英美等发达国家教育界于20世纪80年代中后期发展起来的一门多元统计分析新技术,是当前国际上统计学研究中一个新兴而重要的领域[1]。1995年英国伦敦大学教育研究所学者在与北京中央教育学研究所的学术交流活动中首次介绍了多水平统计模型及其在教育研究中的应用,随后出现大量多水平模型的应用报告[2-4],主要用于研究多水平数据[1]或具层次结构以及嵌套结构的数据,如分层抽样或整群抽样的数据。多水平数据的主要特征是反应变量的分布在个体间不具备独立性,但存在地理距离内、某行政划区内或特定空间范围内的聚集性。在多种研究中存在此类数据,例如学校、医院、场所、地区等均具有不同水平或层次的单位,如水平1(低水平)和水平2(高水平)单位,水平1单位的数据容易在水平2单位下呈现聚集性。为此,本文就多水平统计模型分析方法作简单介绍,以期望公共卫生人员能更广泛地应用此方法。
1 基本原理和形式 1.1 多水平模型提出背景传统统计分析方法具有一些基本假设,比如它要求个体间测量变量具有独立性,若此假设不成立,此时模型参数的估计就会出现偏差,从而影响统计推断结论的可靠性。而实际在很多研究中,如流行病学调查,出于可操作性或经济可行性的考虑,经常采用分层或整群抽样方法来获得研究对象,从而产生层次结构数据,导致搜集的数据在群组闪存在聚集性。此时,如果只用传统方法处理此类数据则存在很多弊端[5]:人为扩大高水平单位特征变量的自由度,或者低估低水平单位间差异、损失大量样本的有效信息且增加犯Ⅰ类错误的概率[6]。而适用于具层次结构数据的多水平模型则能役好处理此类情况[7].它可以有效分析含缺失值[8]或非平衡设计的纵向数据资料。
1.2 基本原理多水平模型又被称为随机系数模型、层次线性模型[9]、混合效应模型[10]、混合模型等,在算法或应用领域的普及程度上略有差异。多水平模型集Ⅱ型方差分析理论和多元统计分析技术为一体,将方差分解到相应层次结构水平上。与传统方法相比,多水平模型把低水平上的随机变异分解到高水平上,有更小的残差标准误[11],提高了模型估计的准确度;多水平模型有更小的-2对数似然值[7],模型拟合更好。
1.3 基本形式 1.3.1 方差成分模型[12]又称随机截距模型,是最基本、最简单的模型形式。以某校不同班级学生成绩的影响因素调查为例,班级为该校的随机样本,其基本形式如下:
(1) 模型中不含任何解释变量(零模型),相当于随机效应方差分析模型。
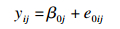
|
(1) |
其中,β0j=β0+u0j,u0j~N(0, σ2u0), e0ij~N(0, σ2e0); i=1, 2, …, n, 表示水平1单位,即某班级不同学生个体;j=1, 2,…,n,表示水平2单位, 即不同班级;aii则表示第j个班级中第i个学生的成绩;u0j表示第j个班级平均成绩β0j与学校学生平均成绩β0的差值,属水平2残差项,其方差σ2u0可用来估计水平2单位之间的差异;e0j为通常的随机误差项,表示不同学生个体间的随机误差,其方差σ2e0可用来估计水平1单位之间的差异。
(2) 模型中可引入任何水平的解释变量,1个或者多个,以引入1个低水平解释变量为例,其形式如下:

|
(2) |
模型中β1是解释变量xij的固定系数;xij表示第j个班级中第i个学生解释变量的测量值。假设xij是学生年龄,yij是学生成绩,则β1表示学生年龄每增加1岁学生成绩的变化。由模型(2) 司以看出,对每个班级学生来说系数β1是相同的,模型拟合的是j条平行线。
1.3.2 随机系数模型[12]又称随机斜率模型,与模型(2) 唯一不同就是解释变量的系数β1j具有随机效应。模型(2) 假定解释变量在所有水平2单位是相同的,但实际应用中常出现水平2单位间此系数是有差异的,如学生年龄每增加1岁,每个班级平均成绩的变化并不一定相同。此时,可将解释变量的系数设为随机变量,最基本的形式如下:

|
(3) |
其中, β0j=β0+u0j, β1j=β1+u1y, u0j~N(0, σ2u0), u1j~N(0, σ2u1), e0ij~N(0, σ2e0), COV(u0j, u1j)=σu01。需估计4个随机参数σ2u0、σ2u1、δ2e0和σu01。σu01指截距和斜率离差值的协方差,反映了二者间的相关关系。
2 模型参数估计及其检验多水平模型含有随机效应成分,它同时提供数据的平均水平信息和变异度信息。将模型(2) 写成yij=(β0+β1xij)+(u0j+e0ij),即固定效应和随机效应2个成分,需要估计固定参数β0、β1和随机参数σ2u0、σ2e0。极大似然法可用于估计固定参数,但由于其未考虑到抽样变异,因而不宜用于估计随机参数。1986年Goldstein[13]提出“迭代广义最小二乘法”,首先利用广义最小二乘法和普通最小二乘法获得随机系数和固定系数的估计粗值,然后在随机与固定参数估计间反复迭代直至收敛。当模型的随机变量在各水平均服从多变量正态分布时,迭代广义最小二乘法等价于极大似然法,估计量基本一致,但小样本时其估计有偏。1989年Goldstein[14]进一步提出“限制性迭代广义最小二乘法”,等价于限制性极大似然法,是无偏估计。迭代时仅用二项分布的均值和方差进行参数估计的方法称为拟似然法,衍生生成预测性拟似然法[15]和边际拟似然法,两法各有优缺点,1996年Goldstein等[16]提出过预测性拟似然法的一些算法。对于固定部分参数构建的假设检验方法有3种,其结果相似:(1) 建立参数的单独可信区间和联合可信区间进行假设检验;(2) Wald检验;(3) 对数似然比检验。对于随机部分参数构建的假设检验,样本量大时可用以上3种方法,其中对数似然比检验方法更好。多水平模型中高水平单位属于某一总体,研究者可以通过残差估计预测高水平单位的个体估计值[12],既体现单位间的随机变异,也可看成是各单位对反应变量的效应成分。在调整全部低水平单位的特征和部分高水平单位的特征后,通过对高水平单位残差估计值进行排序和比较,可识别具极端值的高水平单位,在高水平残差图中容易判断异常点[17]。如果进一步再对其作深入个案调查,则形成意义较大的定量与定性相结合的研究。
3 应门条件及其检验用实际数据拟合模型时,为探究高水平效应是否存在,除密切结合专业知识和具体情况判断外,还可从以下几方面考虑:(1) 拟合零模型①,并检验随机参数σ2u0,若具有统计学意义则存在高水平效应;(2) 计算组内相关系数(intra-class correlation coefficient,ICC)或者方差分配系数(variance partition coefficient,VPC)[18],二者表示高水平变异或方差占总变异或方差的比例;(3) 与传统模型相比较,检验是否具有较小的-2对数似然值;(4) 高水平残差是否为0。若综合以上各方法后判断数据层次结构无实际意义,则直接选用传统模型进行分析与交流即可。
多水平模型也存在一定的模型假设:各水平残差服从正态分布和模型的常数方差性。分别对各水平作标准化残差正态分布图,以该水平变量的标准化残差为纵轴,以其正态分数为横轴,若呈直线则基本认为该水平残差符合正态分布,适合构建多水平模型。
多水平模型要求高水平单位和低水平单位都要有足够样本量。低水平单位数量较少时,高水平残差估计能利用相互借助的力量在一定程度有效地节制极端的估计;但低水平单位数量过少时,此残差估计值会很小,层次结构不明显,此时构建多水平模型则不合理,易得出有偏结论;有学者建议将低水平单位 < 5个的不纳入分析[19]。另外,由于方差成分估计值的准确性依赖于估计方差成分的自由度,高水平单位数量过少( < 5) 也会导致固定效应及其标准误的估计有偏。
4 应用资料及模型类型多水平模型已应用于多类型的层次结构数据中,对应产生不同多水平模型形式,如二分类离散数据多水平模型、多分类离散数据多水平模型、重复测量数据多水平模型、多水平交叉分类模型、多水平meta分析模型和多水平生存时间模型等。流行病学中多以离散型变量为研究因素,部分具层次结构的数据服从超二项、超Poisson模型,可引入多水平模型分析方法,如多水平logistic回归模型[20]、多水平Poisson回归模型[21]、由Poisson回归模型扩展而来的多水平空间模型;反应变量为多分类变量(无序或有序)时,可引入多分类多水平模型拟合数据,连续型变量也可转化后纳人多分类反应变量多水平模型。
重复测量资料具有个体测量值非独立、相关性强和变异来源多等特点。Goldstein等[22]提出多水平时间序列模型用于儿童生长发育研究产生的重复测量数据。国内学者指出多水平模型应用于纵向数据时需考虑的原则[23]:至少需要 > 3次的追踪数据、根据研究需要合理选择时间变量、最低水平中结果变量必须在各次测量中具有等价性及可比性。Crystal等[24]运用多水平模型对艾滋病患者的不平衡纵向数据进行分析,显示艾滋病患者功能损伤的时间趋势,利用传统模型却未发现时间趋势关系,可见多水平模型在处理包含缺失值或不平衡数据的纵向数据时很具灵活性。
多水平meta分析模型应用也较多,优点是能分析各研究差异的大小和来源。多水平模型拟合meta分析数据时,纳入分析的研究本身为水平2单位,研究中包含的对象为水平1单位[25];此时考虑了各研究之间的变异,但由于多数情况下不能得到原始研究中所有研究对象个体的资料,使其模型不同于一般意义上的多水平模型。
5 广泛应用及展望目前多水平统计模型广泛应用于教育、心理、社会、经济、政治、地理等领域[26-27],在实验研究、儿童生长发育、流行病学及其他医学领域中也应用广泛。随着计算机技术的发展,现已建立起一套可以常规应用的技术与软件,由Goldstein领导开发的MLwiN软件作为多水平分析的专用软件,可以拟合多个水平多种类型的模型,功能实现简便;此外,SAS、SPSS、Stata、SPlus、MPlus和LISREL等软件也可实现较为基本但程度不同的多水平分析。综上所述,多水平模型应该并且可以在实际研究的数据分析中得到更多的应用,使推断结论更可靠,当然,在具体实践应用中应符合该模型的一般特征和要求。
| [1] | Goldstein H. 多水平统计模型[M]. 李晓松, 译. 2版. 成都: 四川科学投术出版社, 1999: 1-8. |
| [2] | 杨珉. 多水平统计模型在生长发育研究中的应用(一)[J]. 中国卫生统计, 1997, 14(3): 58–60. |
| [3] | 李晓松, 倪宗瓒. 多水平logistic模型在问卷信度研究中的应用[J]. 中国卫生统计, 1998, 15(6): 1–4. |
| [4] | 金芳, 倪宗瓒, 李晓松, 等. 多元多水平模型在儿童生长发育研究中的应用[J]. 中国公共卫生, 2004, 20(4): 447–448. DOI:10.11847/zgggws2004-20-04-38 |
| [5] | 杨珉, 李晓松. 医学和公共卫生研究常用多水平统计模型[M]. 北京: 北京大学医学出版利, 2007: 3-7. |
| [6] | 彭慧. 多水平模型在中学生预防艾滋病健康教育中的应用[D]. 广州: 中山大学硕士学位论文, 2009. http://d.wanfangdata.com.cn/Thesis/Y1476680 |
| [7] | 衡明莉, 王泓午, 马林茂, 等. 多水平模型在分层抽样研究中的优越性[J]. 首都医科大学学报, 2010, 31(3): 373–376. |
| [8] | 王艳梅, 王洁贞, 丁守銮, 等. 多水平模型在纵向研究资料中的应用[J]. 山东大学学报:医学版, 2007, 45(7): 658–661. |
| [9] | Jostins L, Pickrell JK, Macarthur DG, et al. Misuse of hierarchical linear models overstates the significance of a reported association between OXTR and prosociality[J]. Pro Natl Acad Sci USA, 2012, 109(18): E1048. DOI:10.1073/pnas.1202539109 |
| [10] | Yucel RM. Random-covarianees and mixed-effects models for imputing multivariate multilevel continuous data[J]. Stat Modelling, 2011, 11(4): 351–370. DOI:10.1177/1471082X1001100404 |
| [11] | 李佳萌. 多水平模型在吸烟行为研究中的应用[J]. 中华流行病学杂志, 2007, 28(4): 398–401. |
| [12] | 孙振球, 徐勇勇. 医学统计学[M]. 北京: 人民卫生出版社, 2010: 445-464. |
| [13] | Goldstein H. Multilevel mixed linear model analysis using iterative generalized least square[J]. Biometrika, 1986, 73: 43–56. DOI:10.1093/biomet/73.1.43 |
| [14] | Goldstein H. Restricted unbiased iterative generalized least squares estimation[J]. Biometrika, 1989, 76: 622–623. DOI:10.1093/biomet/76.3.622 |
| [15] | Breslow NE, Clayton DG. Approximate inference in generalized linear mixed model[J]. Journal of the American Statistical Association, 1993, 88: 9–25. |
| [16] | Goldstein H, Rasbash J. Improved approximations for multilevel models with binary responses[J]. Journal of the Royal Statistical Society, 1996, 159: 505–513. DOI:10.2307/2983328 |
| [17] | 王静, 叶冬青. 多水平统计模型简介及MLwiN软件的应用实例说明[J]. 疾病控制杂志, 2006, 10(5): 518–522. |
| [18] | Goldstein H, Browne W, Rasbash J. Partitioning variation in multilevel models[J]. Understanding Statistics, 2002, 1: 223–232. DOI:10.1207/S15328031US0104_02 |
| [19] | Li Q, Li X, Stanton B, et al. A multilevel analysis of gate-keeper characteristics and consistent condom use among establishment based female sex workers in Guangxi, China[J]. Sex Transm Dis, 2010, 37(11): 700–705. DOI:10.1097/OLQ.0b013e3181e1a2b2 |
| [20] | 廖国宇, 周燕荣, 钟晓妮, 等. 重庆15岁及以上城市居民2周患病影响因素的多水平模型[J]. 重从医科大学学报, 2010, 35(8): 1238–1241. |
| [21] | 陈家慧, 富春枫, 赵杨, 等. 多水平Poisson回归模型在交叉设计临床试验中的应用[J]. 中国临床药理学与治疗学, 2007, 12(11): 1306–1310. DOI:10.3969/j.issn.1009-2501.2007.11.023 |
| [22] | Goldstein H, Healy MJ, Rasbash J. Multilevel time series models with applications to repeated measures data[J]. Stat Med, 1994, 13(16): 1643–1655. DOI:10.1002/(ISSN)1097-0258 |
| [23] | 杨会芹, 何俊华. 多层线性模型在心理和教育纵向研究中的运用[J]. 石家庄学院学报, 2008, 10(3): 71-71–102. |
| [24] | Crystal S, Sambamoorthi U. Functional impairment trajectories among persons with HIV disease:a hierarchical linear models approach[J]. Health Serv Res, 1996, 31: 469–488. |
| [25] | Flückiger C, Del Re AC, Wampold BE, et al. How central is the alliance in psychotherapy? A multilevel longitudinal meta-analysis[J]. J Couns Psychol, 2012, 59(1): 10–17. DOI:10.1037/a0025749 |
| [26] | 贾红, 张俊辉, 李爱玲, 等. 健康城市建设满意度多水平模型评价[J]. 中国公共卫生, 2012, 28(4): 458–461. DOI:10.11847/zgggws2012-28-04-17 |
| [27] | 赵倩倩, 杨永利, 施学忠, 等. 河南省卫生系统反应性影响因素多水平模型分析[J]. 中国公共卫生, 2011, 27(6): 762–764. DOI:10.11847/zgggws2011-27-06-38 |
 2017, Vol. 33
2017, Vol. 33


