数据主要分为名义数据、有序数据、区间数据和比率数据4类,其中,名义数据和有序数据统称为定性数据,区间数据和比率数据统称为定量数据。有序数据是将观察单位按某种属性的不同程度分成等级后分组计数,分类汇总各组观察单位数后而得的资料[1]。目前,有序数据在医学科学研究中的应用已屡见不鲜。有序数据的各个类别形成了一个有序而封闭的结构,这个结构会受到1个或多个外部因素的影响,因此将有序数据作为一个整体进行分析和探索在医学统计中鲜有人尝试。信息熵是一种测量结构信息量的理论和方法[2]。本文从信息理论的视角,对有序数据结构进行了整体性的度量,在经过统计学变换和多重线性回归分析后,实现了对有序数据结构外部影响因素的测量,为有序数据的分析提供了一种新的思路和方法。
1 原理与方法一个结构可以由多个类别构成,所有类别的比重合计为100%,一个类别的比重变化会引起其他类别比重的变化。结构的表观特征一般用构成比来描述,结构的内在核心特征是结构所包含的信息量;从一般的表观特征抽象出核心特征,即得到一个结构所包含的信息量。结构的信息量度量用信息熵表示,信息熵即为entropy,公式为:
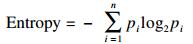
|
(1) |
其中,n为结构的类别数;i为第i个类别(1≤i≤n);Pi原指信源发出各种符号的频率或概率[2],这里表示结构第i类别的构成比。然而,在各类别构成比保持不变的情况下,不同的排序方式,信息熵值并不改变。因此,信息熵不能直接用来衡量有序数据结构的信息量。为了测量李克特量表的答题一致性,基于信息熵理论提出了一致性指数(agreement,AGR),公式为:
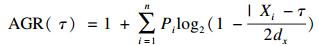
|
(2) |
其中,n为有序结构的类别数;i为第i个类别(1≤i≤n);Pi为有序结构第i类别的构成比;Xi为有序结构第i类别的赋值;τ为可人为设定的期望均值;dX为有序结构(变量X)的宽度;X为随机离散变量[3-4]。此处以药物疗效为例,药物疗效分为治愈、显效、好转、无效4个等级,赋值为:治愈=1、显效=2、好转=3、无效=4。那么X={1,2,3,4},并且X1=1,X2=2,X3=3,X4=4。dX为变量X的宽度:dX=Xmax-Xmin=4-1=3。τ为我们期望的均值,例如治愈是我们想得到的结果,则可设定τ=1。AGR的取值范围为[0, 1],为了能清楚说明AGR的性质,假设有10种骨质疏松药物分别治疗20个患者的疗效结果,见表 1。第1种药物显示,所有个体疗效均无效,距离期望的治愈最远,因此AGR=0;第10种药物显示,所有个体疗效均为期望的治愈,AGR=1;从第1种药物到第10种药物,疗效逐渐靠近期望的治愈,AGR也从0越来越接近1。简而言之,药物疗效结构越好,AGR越大。从数学意义上讲,AGR是一种描述有序数据离散程度的统计指标,距离期望的均值τ越近,有序数据的离散程度越小,此时AGR就越大。从表 1可以看出,若以治愈为期望的均值,从第1种药物到第10种药物,数据的离散程度是逐渐变小的,对应于AGR从0变化到1。因此,AGR可以较好地反映有序数据距离期望均值的整体分布状况。另外,AGR与各等级类别的实际频数无关,而是与各类别所占的百分比有关,因此可用于不同对象的直接比较[5],而不用考虑各对象的实际总频数是否相等。
| 表 1 不同药物疗效结构的AGR变化情况 |
大数据模拟实验表明,对AGR进行logit变换,变换后的值y服从正态分布,取值范围为(-∞,+∞)。此时即可采用多重线性回归的方法测量外部因素对有序数据结构的影响。应当注意的是,当AGR等于或者接近1或0时,y值趋近无穷大,此时需要注意离群值对结果的影响。有序数据结构外部影响因素测量的回归方程:
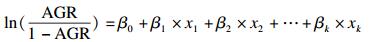
|
(3) |
x1,x2,…,xk为纳入模型的影响因素;β1,β2,…,βk为对应的偏回归系数;β0为截距。根据公式(3) 可得到AGR:
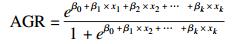
|
(4) |
如果βj为正,在其他变量保持不变时,AGR随xj的增大而增大;如果βj为负,在其他变量保持不变时,AGR随xj的增大而减小。
2 实例分析某研究调查了中国450个村/社区的基本情况,以及这些村/社区中≥45岁中老年人的健康自评状况(很好、好、一般、不好、很不好)[6]。各个村/社区中老年人的整体健康状况可以用AGR来衡量,运用上述方法即可分析地区类型、下雪天数、下雨天数、有无公共厕所、有无下水道系统、有无露天健身器材、有无老年活动中心、有无老年协会、是否设置最低生活保障金、是否给≥65岁老人发放补助等10个因素对村/社区中老年人整体健康状况的影响。此研究共调查了145个城市社区和305个乡村行政单位,中老年人共计17 577人,其中健康状况很好、好、一般、不好、很不好的人数分别为1 338人(7.61%)、2 864人(16.29%)、8 169人(46.48%)、4 723人(26.87%)、483人(2.75%)。将健康状况很好作为期望的类别,450个村/社区的AGR的最大值为1.00,最小值为0.33,平均值为(0.57±0.08)。其中,农村中老年人整体健康状况AGR的(0.55±0.07),低于城市社区中老年人整体健康状况AGR为(0.61±0.06),差异有统计学意义(t=-8.889,P < 0.000 1)。对AGR值进行logit变换,以logit变换后的值为因变量,以下雪天数、下雨天数、有无公共厕所、有无下水道系统、有无露天健身器材、有无老年活动中心、有无老年协会、是否设置最低生活保障金、是否给≥65岁老人发放补助等待研究的9个因素为自变量,采用逐步回归的方法(入选标准为0.05,剔除标准为0.10) 分别对乡村和城市社区进行多重线性回归分析。结果显示,给≥65岁老年人发放补助、有下水道系统、有露天健身器材的乡村,中老年人整体健康状况相对较好;下雪天数越少、有露天健身器材的城市社区,中老年人整体健康状况相对较好,见表 2。
| 表 2 乡村和城市社区中老年人健康状况影响因素分析 |
3 讨论
AGR能够准确而灵敏地反映有序数据结构的变动情况,本文实例用来衡量各个村/社区中老年人的整体健康状况,并探索了能导致慢性病发生、发展的社会环境因素[7]。本文介绍的方法具有以下特点:(1) 运用AGR可对多个有序数据结构进行直接比较,例如可以比较各个村/社区中老年人的整体健康状况,并进行各个村/社区整体健康状况的排序,可以简便快速地发现健康状况最差的几个村/社区,以便于进行健康干预;不足之处在于不能对不同村/社区中老年人的整体健康状况的分布进行假设检验。传统的非参数检验方法可以用来比较各个村/社区健康状况的分布,但是随着村/社区数目的增多,两两比较次数的增长也越来越快,不仅工作量大,而且很难对各个村/社区的整体健康状况进行排序。因此,在处理有序数据时,AGR和传统的非参数检验方法是一对优势互补的方法,将两者结合起来使用可以得到更加全面的结果。(2) 同样是文中的数据,有序logistic回归可以探索个人层面的影响因素,比如年龄、婚姻状况、文化程度等[8-9],而AGR进行logit变换后,以有序数据结构整体为单元,能够探索更加宏观的影响因素。例如本文实例中探索的是村/社区层面的影响因素(村/社区是否发放老年人补助、是否有露天健身器材等),可以为村/社区的建设提供指导性建议。因此,这2种方法在实际运用中的侧重点有所不同,要根据研究目的和数据结构特点进行合理地选择和利用。此外,有序多水平模型可以同时探索个人层面和更高水平(例如社区)的影响因素[10],但是由于有序多水平模型的构建比较复杂,目前在公共卫生领域的应用较少。(3) 该方法是一种基于信息理论的新方法,在医学大数据背景下,医学中广泛存在的待研究的有序数据结构,使得该方法有较大的应用价值和现实意义。
但是,在应用本文中探讨的方法时需要注意以下3个方面:第1个方面是有序数据结构中相邻的两等级分类间的距离实际上并不一定相等,例如治愈到显效的距离并不一定等于显效到好转的距离,而在文中是假定距离相等,即设定的治愈=1、显效=2、好转=3、无效=4。解决这个问题的一个方法是赋予各等级分类不同的权重[11],例如通过专家评分法衡量各等级分类间的距离,第1个等级分类治愈=1和最后1个等级分类无效=4保持不变,重新设定显效=1.8、好转=2.5,此时X1=1、X2=1.8、X3=2.5、X4=4,即可计算AGR。第2个方面是有序数据结构中可能会存在“地位”不同的个体或群体[11]。例如在计算某医院病人病情程度(危、急、一般)的一致性指数时,由于主任医师、主治医师、住院医师的知识和经验不同,对病人病情程度的判断结果可能会存在差异,因此需要对不同职称医生评定的病人病情程度赋予不同的权重。至于权重分配的比例要视具体情况进行斟酌,不能一概而论。第3个方面是本文中介绍的方法在运用于小样本数据时,AGR经过logit变换后并不一定服从正态分布,如果继续运用多重线性回归分析方法不大合适。尤其是当AGR等于或者接近1或0时,logit变换后的值趋近正、负无穷大,对分析的结果会产生较大的影响,这时就需要对强影响点进行相应的处理,以提高回归方程的质量[12]。
志谢 感谢北京大学国家发展研究院中国经济研究中心提供CHARLS数据| [1] | Sousa RG, Yevseyeva I, Costa JFPD, et al. Multicriteria models for learning ordinal data:a literature review[J]. Artificial Intelligence, Evolutionary Computing and Metaheuristics, 2014, 427: 109–138. |
| [2] | 付沙, 周航军, 杨波, 等. 基于信息熵多属性决策的统计信息综合评价研究[J]. 现代情报, 2015, 35(8): 126–130. |
| [3] | Tastle WJ, Wierman MJ.Adjusting the consensus measure to target ordinal scale arguments[C]// Fuzzy Information Processing Society, 2006.Nafips 2006 Meeting of the North American, 2006:403-407. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4216836 |
| [4] | Tastle WJ, Wierman MJ.Agreement, agreement distributions, and distance[C]// Fuzzy Information Processing Society, 2008.Nafips 2008 Meeting of the North American, 2008:1-4. http://ieeexplore.ieee.org/document/4531271/ |
| [5] | Tastle WJ, Wierman MJ. Consensus and dissention:a measure of ordinal dispersion[J]. International Journal of Approximate Reasoning, 2007, 45(3): 531–545. DOI:10.1016/j.ijar.2006.06.024 |
| [6] | Zhao Y, Hu Y, Smith JP, et al. Cohort profile:The China Health and Retirement Longitudinal Study(CHARLS)[J]. International Journal of Epidemiology, 2014, 43(1): 61–68. DOI:10.1093/ije/dys203 |
| [7] | 秦江梅. 中国慢性病及相关危险因素流行趋势、面临问题及对策[J]. 中国公共卫生, 2014, 30(1): 1–4. DOI:10.11847/zgggws2014-30-01-01 |
| [8] | 白思敏, 谢慧玲. 基于有序logistic回归的乌鲁木齐市≥65岁社区老年人自评健康影响因素分析[J]. 中国卫生事业管理, 2015(2): 96–98. |
| [9] | 吴振强, 崔光辉, 张秀军, 等. 老年人家庭功能状况及影响因素分析[J]. 中国公共卫生, 2009, 25(2): 138–140. DOI:10.11847/zgggws2009-25-02-06 |
| [10] | 郭仲琪. 基于贝叶斯估计的有序多分类多层模型的应用[D]. 广州: 广东药学院硕士学位论文, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10573-1014009382.htm |
| [11] | Tastle WJ, Wierman MJ.Using consensus to measure weighted targeted agreement[C]// Fuzzy Information Processing Society, 2007.Nafips'07 Meeting of the North American, 2007:31-35. http://ieeexplore.ieee.org/document/4271029/ |
| [12] | Tohidi M, Ghasemi A, Hadaegh F, et al. Age-and sex-specific reference values for fasting serum insulin levels and insulin resistance/sensitivity indices in healthy Iranian adults:Tehran Lipid and Glucose Study[J]. Clinical Biochemistry, 2014, 47(6): 432–438. DOI:10.1016/j.clinbiochem.2014.02.007 |
 2017, Vol. 33
2017, Vol. 33


