虽然近年来全球疟疾控制取得了显著而持久的进展，但疟疾目前仍是全球最受关注的传染病之一。据估计，2013年全球有33亿人口处于疟疾感染的危险中，疟疾新发病例1.98亿，58.4万人死于疟疾^[1]。对疟疾流行趋势进行预测有助于提前采取有针对性的防控措施并合理地配置卫生资源。因此构建灵敏的疟疾流行早期预警方法是疟疾防控工作的研究内容之一。气象因素是疟疾流行的重要影响因素，针对特定地区建立疟疾气象预测模型是构建疟疾早期预警系统的重要方法^[2]。

人工神经网络是模拟生物神经网络进行信息处理的一种数学模型，它具有大规模并行分布式结构、自主学习能力以及由此而来的泛化能力^[3]。Back propagation(BP)神经网络是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一，在统计学领域主要将它应用在预测、判别分类问题中，近年来也常用于解决医学领域的问题^[4-8]。

万宁市位于中国海南岛东南沿海，是中国著名的疟疾高发区。万宁疟疾流行具有明显的季节性，市内高疟区主要分布于西南部山区丘陵地带，主要媒介是大劣按蚊和微小按蚊。为分析气象因素与万宁市疟疾发病率的相关性, 比较BP神经网络模型和逐步回归模型对疟疾发病的预测效果，本研究收集1995年1月－2007年12月万宁市每月气象数据和疟疾发病率数据，应用Spearman等级相关分析方法分析气象因素与疟疾发病率之间的相关性，分别用BP人工神经网络方法和逐步回归方法建立疟疾发病率的气象因子拟合模型，预测2008年各月的疟疾发病率。结果报告如下。

收集1995年1月－2008年12月万宁市疟疾月发病率数据，数据由万宁市卫生防疫站提供。1995年1月－2002年12月万宁市每月平均气温、最高气温、最低气温、平均相对湿度、降雨量、日照时间、平均气压数据由海南省气象局提供，2003年1月－2008年12月相应数据由国家统计局提供。

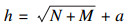
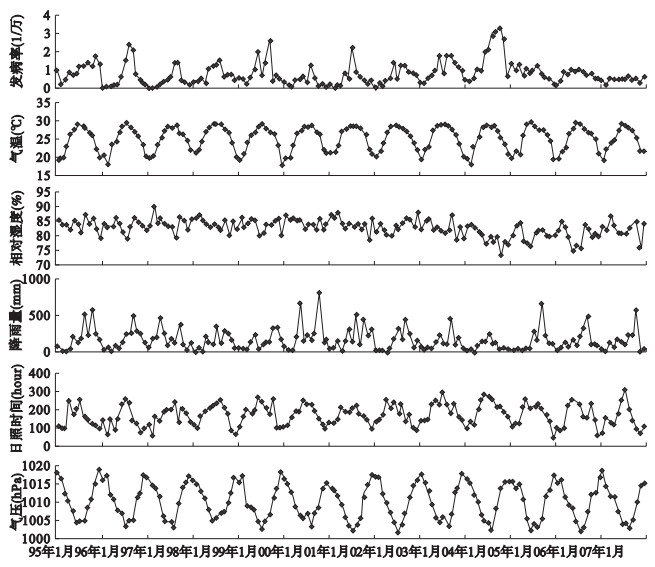
应用SPSS 15.0统计软件进行Spearman等级相关分析，分析气象因素与疟疾发病率的相关性，并构建疟疾发病率的逐步回归模型。应用matlab 7.0软件构建疟疾发病率的BP神经网络模型，输入层数据为1995年1月－2007年11月各月气象数据，输出层数据为1995年2月－2007年12月各月疟疾发病率。用premnmx函数将神经网络输入层数据和输出层数据进行归一化变换，使其值范围为[-1, 1]。本研究采用含一个隐含层的神经网络结构^{[3, 9]}，参考公式确定隐含层单元的数量范围，其中N为输入单元数，M为输出单元数，a为1~10的常数^[10]，通过改变常数a的数值来改变隐含层单元个数h的方法对网络进行训练和调整，直到训练误差达到预先设定的误差最小值为止。本研究预设网络最小训练误差为0.001，最大训练次数为10 000，学习率为0.02，其他参数采用系统默认值。网络训练采用Levenberg-Marquardt训练方法，其训练函数为trainlm。隐含层激活函数为tansig函数，输出层激活函数为purelin函数。该网络的初始结构为：net=newff(minmax(p), [m, n], {‘tansig’, ‘purelin’}, ‘trainlm’)。其中minmax(p)为网络输入p的取值范围，m为隐单元数，n为输出单元数，由于输出单元为疟疾发病率，故n=1。采用决定系数R²检验神经网络模型的拟合效果，其值越接近1，说明模型拟合效果越好。将2007年12月－2008年11月的气象数据分别代入BP神经网络模型和逐步回归模型，分别得到2种模型2008年1－12月的疟疾发病率预测值，利用预测值的平均绝对误差比较2种模型的预测效果。

图 1

图 1 万宁市1995－2007年气象状况及疟疾月发病率时间序列

万宁市1995－2007年各月疟疾发病率及平均气温、最高气温、最低气温、平均相对湿度、降雨量、日照时间、平均气压变化情况见图 1。相关分析结果显示，疟疾的月发病率与其前1个月的平均气温(r=0.61，P < 0.01)、最高气温(r=0.57，P < 0.01)、最低气温(r=0.54，P < 0.01)、降雨量(r=0.17，p=0.04) 和日照时间(r=0.58，P < 0.01) 均呈正相关，与其前1个月的平均相对湿度(r=-0.29，P < 0.01) 和平均气压(r=-0.59，P < 0.01) 均呈负相关。

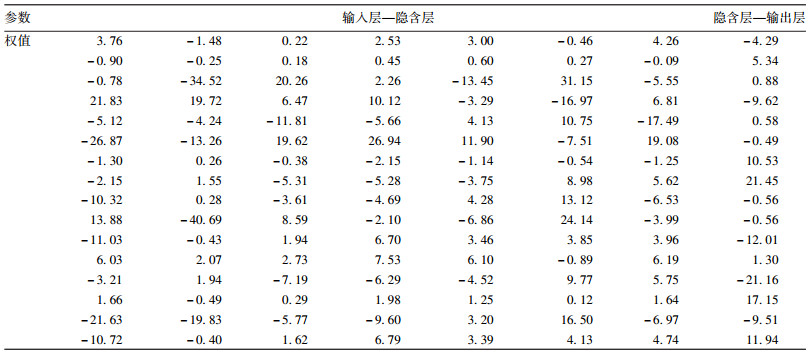
表 1

表 1 BP神经网络模型各神经层单元之间连接权值

表 1 BP神经网络模型各神经层单元之间连接权值

将平均气温、最高气温、最低气温、平均相对湿度、降雨量、日照时间、平均气压7种气象因素作为输入变量，疟疾发病率作为输出变量，通过反复调试确定网络隐含层单元数为16时拟合效果最优，即net=newff(minmax(p), [16, 1], {‘tansig’, ‘purelin’}, ‘trainlm’)是效果相对更好的网络。该模型经过300次训练以后达到预先设定的最小误差值为0.001，模型输出结果的均方误差和决定系数R²分别为0.0027和0.9900，网络拟合效果较好。网络输入层与隐含层之间权值和隐含层与输出层之间权值见表 1。

对疟疾发病率的正态性检验结果显示，疟疾发病率为非正态分布(W=0.14, P < 0.01)。为进行逐步回归分析，对发病率进行平方根转换，转换后数据符合正态分布(W=0.99, p=0.15)。将平均气温、最高气温、最低气温、平均相对湿度、降雨量、日照时间、平均气压7种气象因素作为自变量，疟疾发病率作为因变量构建逐步回归模型，结果显示，进入模型的变量为平均气温和平均相对湿度，疟疾发病率的逐步回归模型为：月发病率=(1.76+0.06×前1个月平均气温-0.03×前1个月平均相对湿度)²，模型的决定系数R²为0.40。

表 2

表 2 万宁市2008年1－12月逐步回归模型和BP神经网络模型疟疾发病率(1/10 000) 预测值比较

表 2 万宁市2008年1－12月逐步回归模型和BP神经网络模型疟疾发病率(1/10 000) 预测值比较

应用BP神经网络模型和逐步回归模型预测万宁市2008年1－12月的疟疾发病率，2种模型预测值的平均绝对误差分别为1.24/10 000和0.44/10 000，逐步回归模型的预测效果优于BP神经网络模型。

研究表明，海南省疟疾流行的消长与气象因素密切相关，可以利用气象因子对疟疾发病率进行预测。本研究结果显示，万宁市的疟疾发病率与前1月平均气温、最高气温、最低气温、降雨量和日照时间均呈正相关，与其前1月平均相对湿度和平均气压均呈负相关。与江苏^[13]、西藏墨脱^[14]、广东广州^[15]等地区疟疾发病率与相对湿度呈正相关不同，万宁市疟疾发病率与相对湿度呈负相关，与在云南省热带雨林地区进行的一项调查结果一致^[16]，同时与尼泊尔的一项调查结果一致^[17]。有研究表明，相对湿度> 60%地区的相对湿度就不再成为疟疾传播的限制性因素^[18]，这种高湿度通过何种机制形成与疟疾发病率的负相关仍需进一步研究。

有研究认为人工神经网络预测法较传统的回归预测法预测效果更好^{[19, 20]}。本研究在相关性分析基础上，尝试应用BP神经网络建模方法构建疟疾发病率的气象因素预测模型，并对其预测效果与常用的逐步回归方法建立的预测模型进行比较。研究结果显示，应用所建立的BP神经网络模型进行回代预测，仿真误差为0.002 7，决定系数R²为0.990 0，说明该模型对训练数据集有非常好的拟合效果。但在对训练集外的样本进行预测时，平均绝对误差为1.24/10 000，大于回归模型预测值平均绝对误差的0.44/10 000，提示BP神经网络模型虽然拟合效果优异，但外推能力尚不够强大。

对疾病的流行趋势进行预测，是流行病学研究的一个热点领域。传统的统计预测如回归预测模型常常要求指标满足正态性、独立性条件，并且在处理复杂非线性问题时存在一定的局限性，而神经网络是一种非线性映射系统，且不要求变量满足正态性、独立性等条件，所以神经网络是一种非传统的信息处理系统。数学理论已证明BP神经网络具有实现任何复杂非线性映射的功能，能以任意精度逼近任何非线性连续函数^[21]，因此对变量间的非线性关系具有较高的建模和拟合能力，常被用于预测和判别分类。但人工神经网络应用中也存在一些问题，例如对于神经网络的类型和结构的选取目前并无统一的标准，而网络结构、神经元数目和神经元类型的选取可直接影响网络的性能。网络隐含层单元数目的选择需要根据设计者的经验和多次实验来确定，不存在一个理想的解析式来表示。当网络的训练样本过多，受到个别特殊样本及噪声的影响，网络学习会出现“过拟合”现象^[22-23]，不能得到样本内含的规律，从而丧失网络的泛化能力，即网络对新样本的预测能力。另外，神经元之间权重系数的假设检验以及流行病学意义等也需要进一步研究。本研究结果显示，BP神经网络模型用于疟疾发病率的预测效果并不优于传统的逐步回归模型，如何结合具体问题对BP神经网络模型进行改进，提高其泛化能力，仍需进一步研究。