中国公共卫生  2017, Vol. 33 Issue (5): 760-763   PDF    
引用本文
王永斌, 许春杰, 尹素凤, 武建辉, 柴峰, 李向文, 袁聚祥. 中国手足口病发病率ARIMA、RBF及ARIMA-RBF组合模型拟合及预测效果比较[J]. 中国公共卫生, 2017, 33(5): 760-763.
WANG Yong-bin, XU Chun-jie, YIN Su-feng, et al. Comparison on predictive capacity and fitting efficiency of ARIMA, RBF and ARIMA-RBF combination model for incidence of hand-foot-mouth disease[J]. Chinese Journal of Public Health, 2017, 33(5): 760-763.
中国手足口病发病率ARIMA、RBF及ARIMA-RBF组合模型拟合及预测效果比较
王永斌, 许春杰, 尹素凤, 武建辉, 柴峰, 李向文, 袁聚祥    
华北理工大学公共卫生学院, 河北 唐山 063000
收稿日期: 2015-11-23; 数字出版日期: 2016-5-19.
基金项目: 河北省卫生厅医学科学研究重点课题(20130055)
作者简介: 王永斌(1989-), 男, 甘肃正宁人, 博士在读, 研究方向:人群传染病防治。
通讯作者: 袁聚祥, E-mail:yuanjx@heuu.edu.cn
摘要：目的 比较求和自回归滑动平均混合模型（ARIMA）、径向基函数神经网络模型（RBF）和ARIMA-RBF组合模型对中国手足口病月发病率的拟合及预测效果，探讨预测手足口病发病率的优化模型。方法 收集2008年1月-2014年12月中国手足口病月发病率资料，基于2008年1月—2014年6月的78个数据分别建立ARIMA模型、RBF模型和ARIMA-RBF组合模型，采用2014年7—12月的6个数据进行外回代验证模型的外推预测效果，评价指标包括相对误差（RE）、平均相对误差（MRE）、均方误差（MSE），均方根误差（RMSE）和平均绝对误差（MAE）。结果 ARIMA模型拟合和预测的MRE、MSE、RMSE、MAE分别为14.006、4.689、2.165、0.916和13.565、4.416、2.101、0.577，RBF模型分别为9.031、1.559、1.249、0.508和8.964、1.504、1.226、0.503，ARIMA-RBF组合模型分别为6.397、1.357、1.165、0.416和6.655、1.485、1.218、0.433，ARIMA-RBF组合模型的拟合及预测曲线与原始值最接近。结论 ARIMA-RBF组合模型拟合及预测效果均优于ARIMA模型和RBF模型。
关键词：手足口病     发病率     求和自回归滑动平均混合模型（ARIMA）     径向基函数神经网络模型（RBF）     ARIMA-RBF组合模型    
Comparison on predictive capacity and fitting efficiency of ARIMA, RBF and ARIMA-RBF combination model for incidence of hand-foot-mouth disease
WANG Yong-bin, XU Chun-jie, YIN Su-feng, et al     
School of Public Health, North China University of Science and Technology, Tangshan, Hebei Province 063000, China
Abstract: Objective To compare predictive capacity and fitting efficiency of autoregressive integrated moving average model (ARIMA), radical basis function model (RBF), and ARIMA-RBF combined model for monthly incidence of hand-foot-mouth disease (HFMD) in China and to explore an optimized model. Methods Data on monthly incidence of HFMD from January 2008 to December 2014 in China were collected and ARIMA, RBF, and ARIMA-RBF combined models were established based on the data; then the data for the period from July to December 2014 were introduced back to the established models to evaluate their predictive capacity.The indexes of fitting efficiency of the models included relative error (RE), mean relative error (MRE), mean square error (MSE), root mean square error (RMSE), and mean absolute error (MAE). Results The MRE, MSE, RMSE, and MAE were 14.006, 4.689, 2.165, and 0.916 for ARIMA fitting model; 13.565, 4.416, 2.101, and 0.577 for ARIMA predictive model; 9.031, 1.559, 1.249, and 0.508 for RBF fitting model; 8.964, 1.504, 1.226, and 0.503 for RBF predictive model; 6.397, 1.357, 1.165, and 0.416 for ARIMA-RBF combined fitting model; and 6.655, 1.485, 1.218, and 0.433 for ARIMA-RBF combined predictive model, respectively.For the three established models, the fitting and predictive values of ARIMA-RBF combined model were closest to the original data. Conclusion The ARIMA-RBF combination model is superior to ARIMA model and RBF model in fitting and prediction of HFMD monthly incidence in China.
Key words: hand-foot-mouth disease     incidence     autoregressive integrated moving average model     radical basis function model     ARIMA-RBF combined model    

手足口病是由多种人肠道病毒引起的一种儿童常见传染病，2008年卫生部列为丙类传染病，其常出现暴发或流行[1]。为此了解其流行规律及流行趋势，对于探索手足口病的病因线索和疾病预防策略及措施的制定具有至关重要的作用。由于手足口病月发病率序列具有季节性特点，采用季节性自回归滑动平均混合模型(autoregressive integrated moving average model，ARIMA)预测手足口病发病是目前最常用的方法之一。ARIMA模型通过对每一个季节周期中相同时间点的序列值进行分析，可以提取其中的季节趋势，并针对每个季节周期内部序列的变化可以提取其中的非季节性成分[2]。但ARIMA模型作为线性模型对数据序列的非线性趋势提取效果较差，而中国手足口病的发病率序列既有线性趋势又有非线性趋势。因此，本研究基于中国2008年1月1日—2014年12月31日手足口病发病序列，将线性ARIMA模型与非线性径向基函数神经网络模型(radical basis function, RBF)进行组合来弥补ARIMA模型非线性映射性能不足的弊端[3]，并比较其与ARIMA模型和RBF模型对手足口病月发病率预测的准确性，以探讨手足口病预测预警的优化模型。

1 资料与方法 1.1 资料来源

资料来源于2008年1月1日—2014年12月31日中国疾病预防控制中心传染病直报系统中各地区上报的手足口病发病序列资料，人口资料来源于中国卫生统计局。

1.2 统计分析

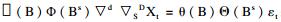
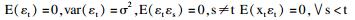
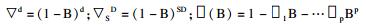
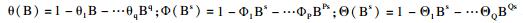
应用SPSS 13.0软件构建ARIMA模型，通过单位根检验来确定序列是否为平稳序列，对于非平稳序列通过对数转换和差分的方式来消除季节和趋势的影响，从而获得平稳的时间序列[2]；依据赤池信息准则(Akaike information criterion，AIC)和Schwarz贝叶斯准则(Schwarz Bayesian criterion，SBC)最小，对数似然函数值(log likelihood)最大的模型为最优ARIMA模型，模型诊断时残差序列应是白噪声，其自相关系数(autocorrelation coefficient，ACF)和偏自相关系数(partial autocorrelation coefficient，PACF)不应与0有显著的差异，Box-Ljung Q统计量应无统计学意义，且模型各系数估计值均应有统计学意义[3]。ARIMA模型公式为：；；；。式中，B为后移算子，εt为残差，d和D分别为非季节和季节差分次数，p和q分别为自回归和滑动平均阶数，P和Q分别为季节自回归和滑动平均阶数[4-5]。应用Matlab 8.0软件建立RBF模型和ARIMA-RBF组合模型时，原始数据序列使用峰值法进行归一化处理。在RBF模型训练过程中，隐含层神经元个数和光滑因子spread的确定是1个关键问题。本研究中利用函数newrbe创建一个精确的神经网络，该函数在创建RBF模型时，自动选择隐含层的数目，使得误差为0[6]。光滑因子spread的确定方法是在用于学习的样本数据中选取6个月的数据作为待估点，将剩余的学习样本数据用来训练神经网络，用训练好的神经网络对这6个待估点进行预测，预测值与实际值的网络逼近误差和均方误差的值最小时对应的光滑因子为最佳spread。通过手足口病发病序列建立ARIMA模型，由于ARIMA模型对手足口病发病序列的拟合值与实际值存在高度的关联性可以将ARIMA模型的拟合值作为RBF模型的输入，实际值作为RBF模型的输出，通过调整光滑因子spread构建1个一维输入、一维输出的优化RBF模型。基于2008年1月—2014年6月的78个数据建立相关模型，用2014年7—12月的6个数据验证模型的外推预测效果，评价指标包括平均相对误差(average relative error，MRE)、相对误差(relative error，RE)、均方误差(mean square predict error，MSE)、均方根误差(root mean squared predict error，RMSE)和平均绝对误差(mean absolute error，MAE)[2]。

2 结果 2.1 ARIMA模型建立及预测(图 1)
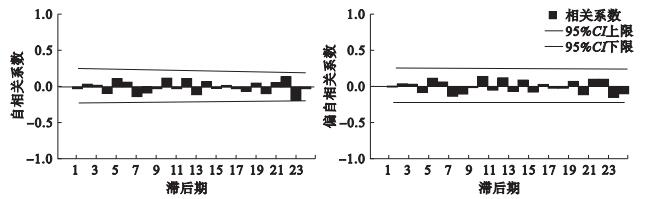
图 1 ARIMA(2, 1, 1)×(0, 1, 1)12残差序列的自我相关函数和偏自我相关函数图

单位根检验结果显示，中国手足口病发病率序列为非平稳时间序列数据。因此首先对原始序列进行对数转换和D=1的季节差分、d=1的非季节差分来消除季节和趋势的影响，从而使序列转化为平稳序列。再结合平稳序列的自我相关函数和偏自我相关函数图、残差序列的自我相关函数和偏自我相关函数图以及相关系数之间的关联性选取log likelihood值最大，AIC和SBC值最小，且模型各系数估计值均有统计学意义的模型为最优模型，通过反复比较，得到最优的模型是ARIMA(2, 1, 1)×(0, 1, 1)12, 具体方程为(1-B)(1-B12)Xt=(1-0.637B)(1-0.448B12)εt/(1-0.891B+0.501B2)，其残差的自我相关函数和偏自我相关函数见图 1。季节性滑动平均系数为0.448(t=3.492，P=0.001)，非季节性滑动平均系数为0.637(t=3.652，P < 0.001)，非季节性自回归系数为0.891(t=6.060，P < 0.001)，AR2=-0.501(t=-4.626，P < 0.001)，AIC=64.078，SBC=75.391，log likelihood=-27.039。且残差序列的Box-Ljung Q统计量差异均无统计学意义(均P>0.05)，可认为残差序列是白噪声。

2.2 RBF模型建立及预测(图 2)
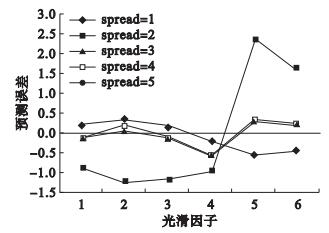
图 2 RBF模型不同光滑因子对应的预测误差

由于手足口病发病率变化的周期为年，因此本研究中RBF模型输入层和输出层神经元个数分别为12和1。光滑因子spread确定时，以2008年1月—2013年12月作为网络的训练样本，2014年1—6月的数据作为网络的测试样本，经多次尝试后，最终确定从1开始，每次增加1直至5，分别得到测试样本的预测值。计算预测值和实际值的网络预测误差、逼近误差和MSE，当它们的值最小时，对应的光滑因子为最优值。本研究中不同光滑因子对应的网络预测误差见图 2，网络逼近误差分别为0.861 6、3.595 1、0.694 6、0.729 6、0.756 9，MSE分别为0.123 7、2.154 1、0.080 4、0.088 7、0.095 5。提示当光滑因子为3时，对应的网络预测误差、逼近误差和MSE的值最小，所以最终确定的光滑因子为3。用确定好的光滑因子构建RBF模型，然后对2014年7—12月数据序列进行预测，将预测值进行反归一化后得到原始序列的预测值。

2.3 ARIMA-RBF组合模型建立及预测(图 3)
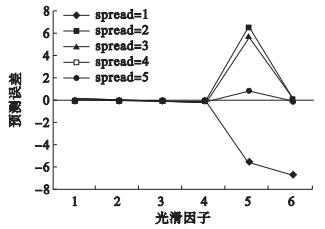
图 3 ARIMA-RBF组合模型不同光滑因子对应的预测误差

构建ARIMA-RBF组合模型时，将ARIMA的拟合及预测值与原始数据序列采用峰值法进行归一化处理。由于对手足口病原始序列进行差分导致13个数据损失，因此以2009年2月—2014年6月ARIMA模型的拟合值作为RBF模型的输入值，以对应月份的手足口病实际发病率作为RBF模型的输出值，构建一维输入、一维输出的ARIMA-RBF组合模型。光滑因子spread确定时，以2009年2月—2013年12月作为网络的训练样本，2014年1—6月的数据作为网络的测试样本。经多次尝试后，最终确定从1开始，每次增加1直至5，最终得到网络逼近误差分别为16.635 8、11.455 7、11.746 7、0.777 2、0.780 4，MSE分别为29.639 2、21.872 3、22.997 6、0.100 7、0.101 5，不同光滑因子对应的网络预测误差见图 3。提示当光滑因子为4时，对应的网络预测误差、逼近误差和MSE的值最小，所以最终确定组合模型的光滑因子为4。用确定好的光滑因子构建ARIMA-RBF组合模型，然后以2014年7—12月ARIMA模型的预测值为输入值，用组合模型对2014年7—12月的数据进行预测，将预测值进行反归一化后得到原始序列的预测值。

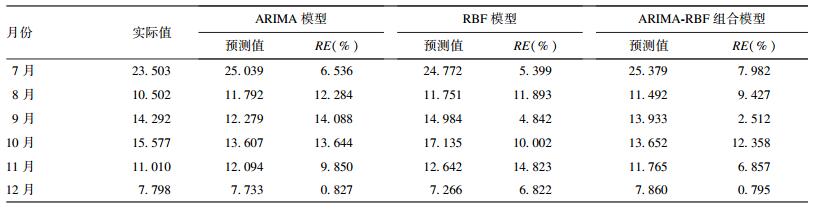
2.4 3种模型拟合及预测效果比较(表 1、图 4)
表 1 中国2014年7—12月手足口病发病率(1/10万)3种模型预测外回代验证值

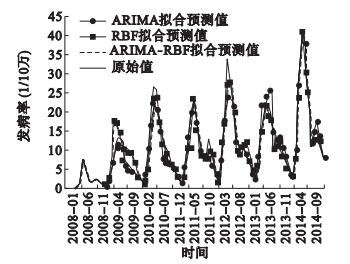
图 4 中国手足口病发病率3种模型对拟合及预测值对比图

ARIMA模型、RBF模型和ARIMA-RBF组合模型3种模型对中国2014年7—12月手足口病月发病率的预测结果见表 1。ARIMA模型拟合和预测的MRE、MSE、RMSE、MAE分别为14.006、4.689、2.165、0.916和13.565、4.416、2.101、0.577，RBF模型分别为9.031、1.559、1.249、0.508和8.964、1.504、1.226、0.503，ARIMA-RBF组合模型分别为6.397、1.357、1.165、0.416和6.655、1.485、1.218、0.433，ARIMA-RBF组合模型的拟合及预测性能均优于ARIMA模型和RBF模型。图 4为3种模型对中国手足口病发病率的拟合及预测曲线，可见ARIMA-RBF组合模型的拟合及预测曲线与原始值最接近。

3 讨论

近年来在医学和公共卫生领域，多种统计预测方法已被广泛应用于疾病发病率、患者预后估计、人口预测、卫生人力资源规划以及各种卫生经费的预算[7]。传染病的发病往往受到多种因素的影响和制约，应用传统的线性模型对其预测存在较大的局限性[8]。而神经网络所具有的非线性映射能力和高度的并行分布处理方式为预测这类非线性动态关系的时间序列提供了一条思路。但单一的线性模型和非线性模型皆存在信息源不广泛问题，在应用中常常受到限制或达不到高精度的要求[9]，而组合预测就是将不同的单一预测模型按一定方式进行组合，综合利用各种方法所能够提供的信息取长补短，具有很强的优势互补性，从而达到提高预测精度和增加预测稳定性的效果。RBF模型具有结构简单、局部响应、快速的训练过程及与初始权重无关的优良特性[6]。因此本研究建立具有ARIMA模型和RBF模型优点的ARIMA-RBF组合模型对我国手足口病发病率进行预测。研究结果表明，ARIMA-RBF组合模型拟合及预测效果优于ARIMA模型和RBF模型。有文献报道，模型拟合及预测的MRE≤10%时，用于预测时准确度和精度较高，其中MRE≤5%时为理想状态[4]。本研究中，ARIMA-RBF组合模型拟合和预测的MRE均≤10%，且ARIMA-RBF组合模型拟合及预测值与实际值的走向有着极为相似的升降规律，提示ARIMA-RBF组合模型更能较好地反映我国手足口病发病率序列的内部规律和未来趋势，是可以推广应用的。但本研究中ARIMA-RBF组合模型拟合及预测效果还未达到理想状态，且目前已有相关研究将ARIMA-BP组合模型[3]、ARIMA-ARCHA组合模型[8]、ARIMA-GRNN组合模型[9]和ARIMA-NARNN组合模型[10]应用于预测传染病发病率，研究结果表明它们的拟合及预测效果优于ARIMA模型，且ARIMA-NARNN组合模型拟合及预测性能优于ARIMA-GRNN组合模型。因此，下一步可考虑将ARIMA-RBF组合模型的拟合及预测效果同上述模型进行比较，寻找预测手足口病发病的最佳组合模型。

尽管本研究中ARIMA模型和RBF模型拟合及预测精度均低于ARIMA-RBF组合模型，但就ARIMA模型和RBF模型拟合及预测的MRE来看，其仍然可以用于预测我国手足口病发病率。需注意的是RBF模型和ARIMA-RBF组合模型建模过中对光滑因子spread的确定是关键，spread的值越大，网络对样本的拟合就越平滑，spread的值越小，网络能更精确地对数据进行拟合。本研究中在学习样本中选取6个月的数据，通过反复训练，综合网络预测误差、逼近误差和MSE来确定最优的spread，从而使模型的拟合及预测性能达到平衡。

综上所述，ARIMA-RBF组合模型在一定程度上具有较高的预测精度与准确度。因此可借助ARIMA-RBF组合模型对我国手足口病发病率进行早期预测、预警，为未来制定相应的政策提供参考依据，从而减少决策的盲目性。但在实际工作中应用组合模型时需注意：(1) 在满足模型使用条件的情况下，根据数据序列的特征，选择合适的单项模型进行组合预测，否则模型的效能不但得不到提高，反而会提供一些不正确的信息；(2) 传染病发病是多因素综合作用的结果，在条件允许的情况下，尽可能多得收集影响传染病发生的因素来构建组合模型；(3) 单次分析构建的组合模型，只适用于短期进行预测。在实际应用过程中，应不断收集新的数据序列对已建立的模型进行外回代验证[11]，以建立更能反映时间序列的内部规律和未来趋势的组合模型。

参考文献
[1] Zhang W, Huang B, She C, et al. An epidemic analysis of hand, foot, and mouth disease in Zunyi, China between 2012 and 2014[J]. Saudi Med J, 2015, 36(5): 593–598. DOI:10.15537/smj.2015.5.10859
[2] Zhang X, Liu Y, Yang M, et al. Comparative study of four time series methods in forecasting typhoid fever incidence in China[J]. PLoS One, 2013, 8(5): e63116. DOI:10.1371/journal.pone.0063116
[3] Zhang G, Huang S, Duan Q, et al. Application of a hybrid model for predicting the incidence of tuberculosis in Hubei, China[J]. PLoS One, 2013, 8(11): e80969. DOI:10.1371/journal.pone.0080969
[4] 王永斌, 郑瑶, 柴峰, 等. 基于周期分解的ARIMA模型在甲肝发病率预测中的应用[J]. 现代预防医学, 2015, 42(23): 4225–4229.
[5] 梅树江, 周志峰, 马汉武, 等. 深圳市ARIMA在肾综合征出血热发病预测中应用[J]. 中国公共卫生, 2015, 31(7): 936–938. DOI:10.11847/zgggws2015-31-07-22
[6] 葛哲学. 神经网络理论与MATLABR2007实现[M]. 北京: 电子工业出版社, 2007: 111-147.
[7] 刘桂芬. 医学统计学[M]. 2版.北京: 中国协和医科大学出版社, 2009: 346-365.
[8] Yan W, Xu Y, Yang X, et al. A hybrid model for short-term bacillary dysentery prediction in Yichang city, China[J]. Jpn J Infect Dis, 2010, 63(4): 264–270.
[9] Zheng YL, Zhang LP, Zhang XL, et al. Forecast model analysis for the morbidity of tuberculosis in Xinjiang, China[J]. PLoS One, 2015, 10(3): e0116832. DOI:10.1371/journal.pone.0116832
[10] Wu W, Guo J, An S, et al. Comparison of two hybrid models for forecasting the incidence of hemorrhagic fever with renal syndrome in Jiangsu province, China[J]. PLoS One, 2015, 10(8): e0135492. DOI:10.1371/journal.pone.0135492
[11] Liu L, Luan RS, Yin F, et al. Predicting the incidence of hand, foot and mouth disease in Sichuan province, China using the ARIMA model[J]. Epidemiol Infect, 2015, 12(3): 1–8.