抽样调查是开展信息收集的重要方式,常见于公共卫生各个领域[1-3]。一项抽样调查能顺利完成,依赖良好的抽样设计。出于对成本和可行性的考虑,目前大多数抽样调查采用复杂抽样设计,其中多阶段抽样是最常见的设计要素之一[4-5]。在这种设计下,样本量如何在各阶段抽样单元中进行有效分配是设计人员面临的重要问题:样本若在总体中过于分散会增加调查样本,降低可行性;若样本过于集中,则可能缺乏代表性,估计不稳定[5]。根据基于设计的分析理论,初级抽样单元(primary sampling unit,PSU)的抽样设计对于估计精度影响较大[6-7],PSU入样比或样本量对抽样误差的估计方式方法及抽样误差的估计精度均有影响,所以样本分配时应首先考虑PSU的样本量。为了解PSU数量与入样比对抽样误差近似估计和统计推断的影响,为今后调查的抽样设计提供参考,本研究收集2010年中国慢性病及其危险因素监测中的98 587条收缩压测量数据开展二阶段模拟抽样,比较不同PSU数量和入样比对误差估计和统计推断的影响。结果报告如下。
1 资料与方法 1.1 资料来源收集2010年中国慢性病及其危险因素监测[8]中全国31个省、直辖市、自治区以及新疆建设兵团162个监测点(区、县或团)98 587名调查对象的收缩压测量数据开展模拟抽样。
1.2 方法以162个监测点共98 587名调查对象的有效收缩压测量值作为总体,进行模拟抽样。由于复杂抽样统计量方差估计形式非常复杂,难以获得显式表达,通常采用极群方差估计策略简化样本结构进行近似估计,即假设样本来自于一阶段整群抽样,忽略除第一阶段抽样外的所有抽样设计[7]。因此,本研究主要对PSU(监测点)的数量或入样比进行模拟,探讨对误差估计和统计推断的影响。根据基于设计的分析理论,统计量的方差(抽样误差的平方)为各抽样层方差之和,各层PSU样本量和入样比对该层抽样误差的影响规律是一致的。为方便理解,本研究不考虑对PSU分层,仅从1个独立层中进行抽样。此外,考虑到样本量对误差估计影响较大,且每个抽样层至少应有2个PSU才能估计抽样误差,本研究将各次抽样样本量定为1 200人,即约2个监测点调查对象总数。每次抽样均包含2个抽样阶段:第1阶段采用简单随机抽样(simple random sampling,SRS)抽取不同数量的PSU,共计40种不同的样本量(2、4、…、48、50)或入样比例(1.2%、2.5%、…、48.1%,49.4%);第2阶段从抽中的PSU中利用SRS抽取相应数量的调查对象,并使每个模拟样本的样本量为1 200人。每个抽样设计均进行500次模拟抽样,总共进行20 000次模拟抽样。
1.3 统计分析应用SAS 9.4统计软件进行模拟抽样。对每个样本计算收缩压的均值、标准误及95%可信区间。一般地,入样比较大时,标准误的计算需要考虑有限总体校正(finite population correction,FPC)[5]。本研究对每个模拟样本均给出考虑和不考虑FPC情况下收缩压均值的标准误。根据本研究的抽样设计,样本收缩压均值可表示为x=∑wij·xij/∑wij,其中xij为第i个PSU的第j个调查对象的收缩压测量值;wij为设计权重,wij=1/(f1·f2),f1和f2分别代表该观测在2个抽样阶段的入样概率。采用泰勒级数线性化估计每个模拟样本收缩压均数的标准误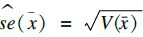
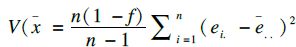
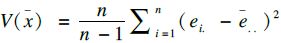
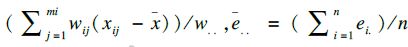
收缩压均值95%可信区间估计采用正态法,为x±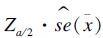
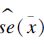
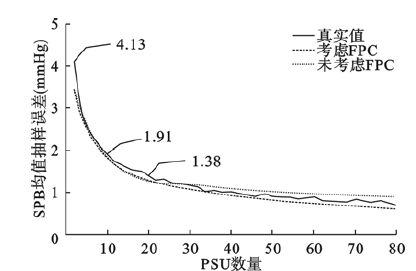
图 1 显示了在不同PSU数量的抽样设计下,抽样误差的近似估计值与真实值。PSU数量自2增加至10,抽样误差迅速从4.13 mm Hg降到1.91mm Hg,下降了53.8%;当PSU数量增加至20,抽样误差降到1.38 mm Hg,降速放缓;之后随着PSU数量增加,抽样误差下降速度越来越慢。考虑FPC和未考虑FPC的误差估计值在PSU为2时均出现了一定程度的低估。在PSU数量较大时(≥20),考虑FPC会造成对抽样误差的低估,反之未考虑FPC会造成对抽样误差的高估,且这种差异会随着PSU个数量的增加而增加。
|
图 1 不同PSU数量情况下抽样误差真值和估计值 |
2.2 统计推断(图 2)
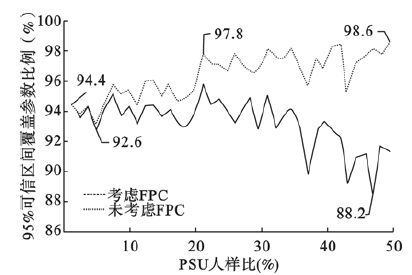
图 2比较了考虑FPC和未考虑FPC在不同PSU入样比情况下估计的均值95%可信区间包含总体均值的概率。在考虑FPC情况下,随着PSU入样比的增加,均值95%可信区间覆盖真值的概率波动较大:在入样比<30%时,95%可信区间覆盖真值概率在94%上下波动,但当入样比>30%时,95%可信区间覆盖真值的概率呈现出震荡下降的趋势,最低到达88.2%,统计推断较敏感。在不考虑FPC情况下,95%可信区间覆盖真值概率均较考虑FPC情况高;在PSU入样比>20%时,95%可信区间覆盖真值概率较入样比<20%时出现了一个小幅跃升,统计推断较保守。随PSU入样比增加,考虑FPC和不考虑FPC情况下进行统计推断的结论差异逐渐增大。
|
图 2 不同PSU入样比情况下95%可信区间估计范围包含真值的概率 |
3 讨 论
本研究通过对一项具有全国代表性的调查数据进行模拟抽样分析,探讨PSU数量及其入样比对抽样误差估计和统计推断的影响。模拟分析显示PSU数量增加至10时,抽样误差下降很快,但增加至≥20时,对于提高估计精度意义不大;随PSU入样比的增加,考虑FPC和不考虑FPC方法的统计推断结论差别逐渐加大。
一项多阶段复杂抽样设计确定样本量后,还需根据调查成本和可操作性,将样本量分配到不同抽样阶段中。样本量的分配决定了调查对象在人群中的离散程度,直接影响调查成本和可行性。理论上,调查样本在总体中越分散,抽样误差越小,估计精度越高;反之亦然[5]。一般地,对复杂抽样调查误差的估计通常会采用简化样本结构的极群方差估计,仅考虑PSU的误差,达到计算的方便性[7]。这种情况下,PSU的数量对抽样误差的估计影响很大。模拟结果显示,抽样误差与PSU数量关系并不是线性的,随着PSU数量增加,抽样误差下降速度是边际递减的。所以,徒增PSU数量并不能获得期望的精度回报,需要找到估计精度和可行性的平衡点。本研究发现,PSU数量从2增加到10的过程中,抽样误差下降非常快;从10增加到20时,误差下降速度明显放缓;但当PSU数量>20时,精度的提升幅度非常小。因此,在调查经费允许情况下,增加PSU数量会增加估计精度,但不建议>20个。
数据分析人员在获得调查数据后,需要根据抽样设计对复查样本的抽样误差进行估计。目前常用的统计分析软件,在默认情况下均采用了极群方差估计策略,仅需要辅以PSU的抽样信息即可估计出抽样误差[6, 11]。一般地,软件假设PSU是有放回或抽自无限总体,所以会忽略FPC。根据经验,认为入样比<5%[5-6]或<10%[11]时,FPC对误差估计的影响较小,可以忽略。本研究模拟结果显示,当入样比<20%时,考虑FPC与不考虑FPC构造的均数95%可信区间覆盖真值概率比较接近。但当入样比>20%时,二者表现差异开始扩大,且不考虑FPC时的统计推断趋于保守,考虑FPC则相反。由于复杂样本抽样误差估计的复杂性,统计分析人员一般更倾向于使用较为保守的方式。但本研究发现,当PSU入样比相当大(如>30%)时,考虑FPC与不考虑FPC表现均不理想:不考虑FPC可能会导致统计推断过于保守,失去了应有的统计效率;考虑FPC则可能会增加I类错误概率。所以,在PSU入样比过大时,极群方差估计策略可能并不是估计抽样误差的有效方法,应考虑多阶段抽样设计,使误差估计更精确。目前,常见统计分析软件,如SUDAAN、Stata和R,均可以实现多阶段抽样设计的误差估计。
本研究利用服从正态分布的血压测量值作为模拟对象探讨了PSU数量和入样比对误差估计和统计推断的影响。虽未对公共卫生领域常见的二项分布数据(率)进行模拟分析,但由于基于设计统计方法并不强调分布假设[6],且样本量较大时二项分布可做近似正态处理,理论上模拟分析也会得到相似的结论。然而,对罕见事件(罕见病)或不独立事件(传染病)抽样调查的PSU抽样设计仍需要更多的模拟研究来支持。
| [1] | 钟韵, 袁红, 钟朝晖, 等. 中国西部两省市农村小学生忽视现状调查[J]. 中国公共卫生, 2015, 31(6) : 713–716. |
| [2] | 龚勋, 王绚璇, 周尚成, 等. 湖北省老年住院患者营养状况调查及评价[J]. 中国公共卫生, 2015, 31(7) : 912–914. |
| [3] | 朱卫红, 黄久仪, 管阳太. 上海市≥ 50岁城镇社区居民脑卒中危险因素调查[J]. 中国公共卫生, 2015, 31(3) : 276–279. |
| [4] | 李镒冲, 于石成, 赵寅君, 等. 基于设计和基于模型方法在复杂抽样数据统计描述中的模拟比较研究[J]. 中华预防医学杂志, 2015, 49(1) : 50–55. |
| [5] | 金勇进, 杜子芳, 蒋妍. 抽样技术[M]. 3版.北京: 中国人民大学出版社, 2012. |
| [6] | Heeringa SG, West BT, Berglund PA. Applied survey data analysis[M].Boca Raton: CRC Press, 2010: 29-31. |
| [7] | Wolter KM. Introduction to variance estimation[M].New York: Springer-Verlag, 1985: 62-68. |
| [8] | 赵文华, 宁光. 中国慢病监测(2010)项目国家项目工作组.2010年中国慢性病监测项目的内容与方法[J]. 中华预防医学杂志, 2012, 46(5) : 477–479. |
| [9] | Lohr SL. Sampling:design and analysis,2nd Edition[M].Boston: Cengage Learning, 2009: 365-391. |
| [10] | SAS Institute Inc. SAS/STAT® 9.2 User's Guide[M].Cary,NC: SAS Institute Inc, 2008: 6485. |
| [11] | United Nations. Department of Economic,United Nations.Statistical Division,National Household Survey Capability Programme.Household sample surveys in developing and transition countries[M].ew York: United Nations Publications, 2005: 449-450. |
 2017, Vol. 33
2017, Vol. 33
