2. 中国疾病预防控制中心性病艾滋病预防控制中心 传染病预防控制国家重点实验室
2013年5月全国新发现HIV(human immunodeficiency virus)感染者/AIDS(acquired immunodeficiency syndrome)病人9 291例,同性性传播1 898例(20.4%)[1]。艾滋病高危人群、特别是男同性恋基数的估计是全面客观分析和掌握该人群基本情况的重要基础,是分析和预测艾滋病流行趋势的核心变量[2]。国际上对艾滋病高危人群基数的估计方法主要有直接法和间接法两类[3, 4]。直接法包括普查法、枚举法等,间接法包括乘数法、网络规模迭加法、提名法和CMR(capture-mark-recapture method)法等。大多数估计方法不能作统计推断或不适合敏感问题的调查,多来源CMR法具有以下几个优点[5]:(1)允许各样本间存在相关。(2)可提高样本的代表性。(3)可基于现存相互重叠的不完整数据库估计目标群体中个体的数目,可挖掘多个方面的现有资料,从而大大减少直接接触调查对象的现场调查。(4)两来源或多来源CMR法可作统计推断,提高了估计的科学性。为此,本研究首次采用三来源CMR法,于2013年11月对北京市MSM人群的基数进行调查,现将结果报告如下。 1 对象与方法 1.1 对象
以2013年10月北京市全部具有本市户籍及在北京市居住6个月以上的常住MSM(the men who have sex with men)人群为研究对象。调查时间为2013年11月。采用两阶段随机抽样方法,根据中国疾病预防控制中心(centers for disease control and prevention,CDC)、北京市各区县CDC、北京MSM群众组织、北京MSM志愿者提供的北京市MSM活动场所、北京市voluntary counselling and testing(VCT)门诊所、男同网站的分布与数量以及北京3个场所的MSM人数大概比例,第1阶段随机抽取北京市28个MSM活动场所、10个VCT门诊所、7个男同网站,第2阶段在已抽取的活动场所、VCT门诊所、男同网站共随机抽取MSM 1 774人,样本按Jianfeng Wang,Ge Gao[6]提出的公式进行估计。 1.2 估计方法
对基数的估计采用三来源CMR法。CMR法起源于对野生动物捕获-标记-再捕获的计数以估计野生动物的数量。当调查对象为人时,CMR法宜称获取-再获取法。三来源CMR法是根据3个来源样本数据资料整理成有1个缺失数据格子的23不完备列联表,如表1。
| 表 1 三来源CMR法的23不完备列联表 |
xijk为观察到的对应格子内的对象个数,下标i、j、k分别代表第一来源、第二来源、第三来源,i、j、k取1代表属于该来源,i、j、k取2代表不属于该来源,表1中“-”代表缺失数据(三来源样本中均未出现的调查对象数)。
三来源CMR法有4种不同模型:(1)三样本中任2对(共3对)样本间相互独立的CMR模型。(2)3样本中有2对样本间相互独立、有1对样本间相关的CMR模型,此时有3种不同形式。(3)3样本中有1对样本间相互独立、有2对样本间相关的CMR模型,此时有3种不同形式。(4)3样本中任2对(共3对)样本间均相关的CMR模型。
本研究采用第(4)种模型,基数N的估计量的计算公式为(其中n为样本含量)[7]:
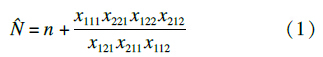
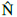 的渐近方差Var(
的渐近方差Var(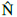 )采用不同内积的正交投影法计算。N的95%CI计算公式为:
)采用不同内积的正交投影法计算。N的95%CI计算公式为:
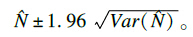
本调查由苏州大学和中国CDC合作进行,结合中国CDC及北京市CDC、北京市各区县CDC的合作项目及北京市CDC、北京市各区县CDC对北京市MSM出入场所开展的日常干预活动进行本次调查。场所认定中,北京市MSM活动场所包括北京市MSM经常出入的酒吧、会所、浴池、公园,VCT门诊所为北京市各CDC、医院、皮防所等单位设立的定点VCT门诊所,男同网站收集的数据为上网IP地址位于北京市的男同网站问卷数据。调查员由医学研究生及CDC、皮防所医师组成,调查员统一培训,各调查场所均有调查员、MSM志愿者向调查对象讲解本次调查的意义,并保证在规定时间内完成问卷填写。同时为了提高调查对象的积极性,为所有参与的调查对象提供一次免费艾滋病、性病体检。 1.4 统计分析
调查数据采用Epi Data 3.1软件建立数据库,所有数据都进行2次核查。采用SAS 9.3软件对所得资料进行处理和计算。 2 结 果 2.1 一般情况
本调查样本人群年龄最小16岁,最大49岁。问卷回收1 774份,其中MSM活动场所519份,VCT门诊所752份,男同网站503份。合格问卷为1 766份,问卷合格率为99.5%,其中活动场所516份,VCT门诊所747份,男同网站503份。 2.2 基数估计(表2)
| 表 2 北京市MSM三来源CMR法的23不完备列联表 |
将此次调查的三来源样本数据整理成有一个缺失格子的23不完备列联表,如表2所示。
将表2中的相关数据代入公式(1),估计得北京市MSM人群的基数为:
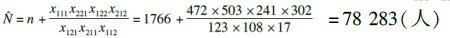
采用不同内积的正交投影法,经SAS编程迭代计算得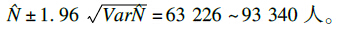 的渐近标准差为:
的渐近标准差为:

北京市MSM人群基数N的95%CI为:
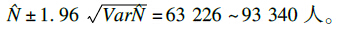
捕获再捕获法基于抽样理论,是通过估计各个来源中均缺失的数据从而估计总体个数以及各种情况的比例[8],当不存在完整的抽样框以建立一种可靠地估计总体的传统抽样调查时,这种方法尤其适用。使用CMR法建立在以下4个假设的基础上[9]:(1)研究域封闭。(2)每个个体被获取的概率相等。(3)每次获取独立。(4)各次获取形式相同。本次调查充分考虑到这些前提条件,并努力优化研究方法。本次调查对象为有北京市户籍与在北京市居住6个月以上的常住MSM人群,且把封闭期设定为1个月,使得研究域封闭这个条件得到保证。本次调查获取的样本是2013年10月到MSM活动场所、VCT门诊所、MSM网站参加活动的MSM人群,而不包括那些在规定期间未参加以上3场所活动(如有固定男性性伴、暂时离京)的MSM对象,前者就成为表1中的7个样本量,后者就成为表1中的缺失数据x222,这很好地符合了CMR法所需要的数据构成。本研究在3个场所均使用了问卷调查这种获取形式,并且考虑到3个场所之间的非独立性,选择了3样本均相关的模型来估计人群基数。本次调查CMR法中三来源选择VCT门诊是一种有益的尝试[10],尤其对于主动求询检测比例较高的北京MSM人群,而网络、活动场所也是众所周知的MSM人群交流的重要渠道,这3类场所可以很好地覆盖北京MSM的出入环境。另外我们选择获取期为1个月,既避免了获取期过短导致收集的资料过少无法满足模型分析的要求,也不会因为获取期过长导致不满足封闭总体的条件。
目前国内外对MSM的研究主要集中在艾滋病病毒感染[11]、行为危险因素[12]及分子流行病学[13]等方面,基数的估计也常局限于不能作统计推断的方法或二来源CMR法。本文考虑到各来源之间独立性在现实调查中难以实现,首次采用三来源CMR法对北京市MSM人群的基数进行调查,并对三来源两两间均存在相关的情况下,拟合合适的对数线性模型,科学估计出北京市MSM人群基数为78 283人,在方法学上具有创新意义。
根据国家统计局北京调查总队发布的2013年北京统计年鉴[14],2012年北京常住人口总量为2 114.8万,其中男性1 090.7万,15~49岁人口1 353.0万,由此估计15~49岁男性约为697.8万(1 068.1/2 069.3×1 314.5),从而得出15~49岁北京市MSM基数约占当地同龄段男性的1.12%(78 283/6 978 000×100%),略高于王丽艳等[15]估计的1%,但低于张北川等[16]在文献中报道的2%~3%。由于男同性恋人群本身的隐蔽性,本文所估计的基数、确切地说应不包括那些从不或极少发生男男性行为的北京市男同性恋人数,恰恰是这些发生男男性行为的男同性恋人群构成了艾滋病的高危人群,已在北京市男性人口中占有不可忽视的比例,因此呼吁相关卫生部门加强对北京市MSM的监测和行为干预。
| [1] | 中国疾病预防控制中心,性病艾滋病预防控制中心.2013年5月全国艾滋病性病疫情及主要防治工作进展[J].中国艾滋病性病,2013,19(7):467. |
| [2] | 许益波.捕获再捕获法在调查杭州市活动型男性同性恋人数中的应用[D].杭州:浙江大学硕士学位论文,2011. |
| [3] | UNAIDS/WHO Working Group.Guidelines on estimating the size of populations most at risk to HIV[M].Geneva:World Health Organization,2010. |
| [4] | 吕繁,张大鹏,贺雄,等.艾滋病高危人群基数估计及其方法[J].中华流行病学杂志,2003,24(11):987-990. |
| [5] | Reddy A.Estimating the size of populations at high risk of HIV in Bangladesh using a Bayesian hierarchical model[M].Washington:UNAIDS,2010. |
| [6] | Wang JF,Gao G,Fan YB,et al.The estimation of sampling size in multi-stage sampling and its application in medical survey[J].Appl Math Comput,2006,178:239-249. |
| [7] | Bishop YMM,Fienberg SE,Holland PW.离散多元分析理论与实践[M].张尧庭译.北京:中国统计出版社,1998. |
| [8] | Rothman KJ,Greenland S,Lash TL.Modern epidemiology[M].Third Edition.America:Lippincott Williams and Wilkins,2008:558. |
| [9] | 陈新华,胡桂华.基于捕获-再捕获模型的人口数目估计[J].统计与决策,2013(22):4-7. |
| [10] | 王国华,谢天胜,辅海平.无固定活动场所MSM人群规模估计方法的应用研究[J].浙江预防医学,2013,25(1):28-30. |
| [11] | 戴丽萍,林玉虾,刘奇,等.广州市不同性角色MSM行为特征及艾滋病感染分析[J].中国公共卫生,2013,29(2):256-258. |
| [12] | 陈向宇,高歌,于明润,等.北京商业性男男性行为Simmons模型调查[J].中国公共卫生,2013,29(2):259-260. |
| [13] | 杜桂英,于海荣.2010年聊城市男男性行为人群艾滋病知识、态度、行为及HIV/梅毒/丙肝感染情况调查[J].预防医学论坛,2013,19(2):93-97. |
| [14] | 北京市统计局,国家统计局北京调查总队.2014北京统计年鉴[M].北京:中国统计出版社,2014. |
| [15] | 王丽艳,夏冬艳,吴玉华,等.乘数法估计北京、哈尔滨两市男性同性恋人群规模的研究[J].华南预防医学,2006,32(3):9-15. |
| [16] | 张北川,李秀芳,史同新.对中国男同/双性爱者人口数量与艾滋病病毒感染率的初步估测[J].中国性病艾滋病防治,2002,8(4):197-199. |
 2015, Vol. 31
2015, Vol. 31


