丙型肝炎(丙肝)是由丙型肝炎病毒(hepatitis C virus，HCV)感染所致的一种慢性肝脏疾病。HCV是一种折叠的单链核糖核酸病毒，属肝炎病毒黄病毒科家族^[1]。自1989年被发现以来，就在世界范围内被认为是导致肝纤维化、肝硬化以及肝细胞癌的主要原因^{[2, 3, 4, 5]}。据报道，全球大约>3%(约1.7亿)的人口感染了HCV^[6]。在中国也存在着丙肝疫情暴发的各种隐患。为此，尽早发现传染病暴发的迹象，及时采取有效控制措施，可有效降低丙肝造成的发病和死亡。为分析不同预测预警方法对江苏省丙肝疫情的预测效果，为丙肝的预防控制提供科学依据，本研究收集江苏省传染病疫情管理系统1997—2009年法定报告传染病疫情中丙肝的发病资料，分别建立Markov链模型、Holt-Winters指数平滑模型以及控制图预警模型，比较3种方法对丙肝预测的效果。结果报告如下。 1 资料与方法 1.1 资料来源

资料来源于江苏省传染病疫情管理系统1997年1月—2009年12月法定报告传染病疫情中丙肝的发病资料。 1.2 方法

1.2.1 Markov随机过程方法

当随机过程在时刻t_n-1状态已知的条件下，其在时刻t_n所处的状态仅与时刻t_n-1的状态有关，这样的过程称为Markov过程。有限个Markov过程的整体称为Markov链，它是由状态转移概率联系起来的一个个状态所组成的“链条”，通过研究链内有限Markov过程的状态及相互关系进而预测链内的未来状况，据此作出决策。疾病的发生的走势属于随机过程，根据疾病资料的取值范围可以划分状态，通过计算状态的频数可以求得各个状态的初始概率，然后再求各状态相互转移出现的频数，确定一阶转移概率矩阵。按照式p_n=p₁ⁿ，可求n阶转移概率矩阵，即是预测值状态间的各阶概率矩阵，按照最大转移概率原理即可作出预测。 1.2.2 指数平滑法

指数平滑预测方法通过给近期的观察值以较大的权重，给远期的实际值以较小的权数，使预测值既反映最新的信息，又能反映历史资料的信息，从而使预测结果更符合实际。指数平滑法可以分为一次指数平滑、二次指数平滑以及多参数指数平滑^[7]。本研究采用的为Holt-Winter季节迭加模型，该方法用于序列具有线性趋势和加法季节变化的序列。y_t平滑后的序列ŷ_t由下式计算：ŷ_t+k=a_t+b_tk+S_t+k,t=s+1,s+2,…,T，其中a_i表示截距，b_t表示斜率，a_t+b_tk表示趋势，S_t为加法模型的季节因子，s表示季节周期长度，月度数据s=12，季度数据s=4。这3个系数有下面的递归式定义： a_t=α(y_t-S_t-s)+(1-α)(a_t-1+b_t-1);b_t=β(a_t-a_t-1)+(1-β)b_i-1; S_t=γ(y_t-a_t)+(1-γ)S_t-s。其中k>0,α、β、γ在0~1，预测值由下式计算： y_T+k=a_T+b_Tk+S_T+k-s，其中S_T+k-s用样本数据最后1年的季节因子。其他模型具体公式参照文献^[8]。

1.2.3 控制图法

按照控制图法预警模型原理，参考国内外传染病预警的一些方法建立控制图法3年模型和控制图法5年模型2种丙肝流行的预警模型。以研究疾病既往3或5年该月的月发病数作为基线数据，计算指定的百分位数(P₅₀、P₆₀、P₇₀、P₈₀、P₉₅)作为候选预警界值，建立预警模型，计算不同预警界值时预警模型的敏感性和特异性，并借助ROC曲线优选出最合适的预警模型及其预警界值。 1.3 统计分析

采用Excel 2003进行数据录入与整理；应用SAS 9.2求转移概率矩阵，采用Eviews 5进行时间序列的分析，应用SPSS 13.0进行统计分析并绘制ROC曲线。 2 结 果 2.1 Markov链模型丙肝疫情预测(图 1、表 1)

根据1997—2008年江苏省丙肝发病的时间顺序及发病数大小，按照所规定的发病数取值范围(状态1:X≤25；状态2：25<X≤50；状态3:50<X≤120；状态4:X>120)确定各年度月发病数所处的状态。各年度月发病数及其趋势见图 1。按照各月发病数所处的状态，计算出各状态相互转移出现的次数，建立一阶转移概率矩阵。应用SAS 9.2求出各阶转移概率矩阵：

图 1

图 1 江苏省1997—2009年丙肝月发病趋势图

表 1

表 1 1997—2009年丙肝各月状态转移次数 状态 1 2 3 4 1 24 9 3 0 2 12 28 2 0 3 0 4 21 9 4 0 0 8 35

表 1 1997—2009年丙肝各月状态转移次数

江苏省1997—2009年丙肝发生病例数总体呈现上升趋势，并且伴随有季节周期性波动，因此选择Holt-Winter季节模型进行拟合和预测。在建模过程中参数值的确定是通过不同参数值的组合进行建模，在参数的选择过程中，要使RMSE最小的模型为最优模型，然后利用最优的参数值组合，通过公式递推出时间序列各时间点的预测值，使拟合和预测达到最佳效果。除此之外MAPE也作为模型拟合效果的评价参考标准。参数设置和最优参数设置如表 2所示，可见Holt-Winter季节迭加模型的RMSE和MAPE 2个指标均低于其他模型，拟合效果较好，因此选择Holt-Winter季节迭加模型对数据进行拟合，将1997—2008年做为训练数据，拟合江苏省实际丙肝发病数，并对2009年各月丙肝发病数做出预测，拟合及预测效果见表 3。Holt-Winter季节迭加模型对2009年各月丙肝发病数的预测相对误差整体较小，除1月的误差略大外，其余各月误差均在较低水平。从宏观分析，该模型对于第2、3季度的预测相对误差较小，效果较好，对于第1、4季度的预测误差较大、效果略差。从图 2可见，Holt-Winter季节迭加模型预测的丙肝发病的趋势与原序列十分接近。

表 2

表 2 指数平滑法参数设置和拟合评估 方法 α β γ RMSE MAPE 一次指数平滑 0.48 16.340 39 24.13% 二次指数平滑 0.14 16.943 21 26.62% Holt-Winter非季节模型 0.45 0.001 16.234 87 25.74% Holt-Winter季节乘积模型 0.14 0.001 0.001 19.839 59 25.35% Holt-Winter季节迭加模型 0.46 0.001 0.001 12.629 85 19.18%

表 2 指数平滑法参数设置和拟合评估

表 3

表 3 Holt-Winter季节迭加模型拟合江苏省2009年丙肝月发病数 月份 发病数(例) 预测数(例) 绝对误差 相对预测误差 1 103 173 70 40.46% 2 145 159 14 8.81% 3 158 177 19 10.73% 4 142 177 35 19.77% 5 175 173 2 1.16% 6 166 172 6 3.49% 7 164 170 6 3.53% 8 156 172 16 9.30% 9 164 164 0 0.00% 10 125 164 39 23.78% 11 145 163 18 11.04% 12 138 152 14 9.21%

表 3 Holt-Winter季节迭加模型拟合江苏省2009年丙肝月发病数

图 2

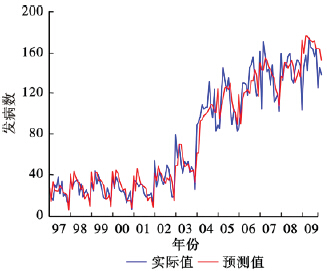图 2 Holt-Winter季节相加模型拟合序列与原序列比较

传染病“流行”系指该疾病的发病水平超过历年一般水平，实际应用时需要对其进行量化。本研究以近5年非流行年发病数为基础，计算丙肝月平均发病数作为基线值，并计算各平均数的s，以作为预警界值判断疾病的流行。将计算所得的基线值代入模型，用各候选预警界值(P₅₀、P₆₀、P₇₀、P₈₀、P₉₅)对2009年江苏省丙肝传染病疫情分月进行预警，并借助ROC曲线优选出最合适的预警模型和预警界值。由图 3可见，选用P₇₀作为预警界值时预警模型的灵敏度和特异度均较好。

图 3

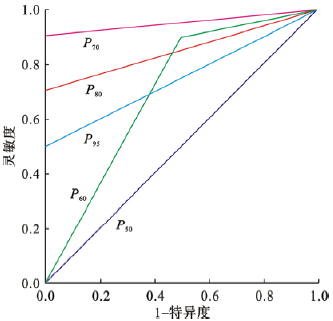图 3 不同预警界值下的ROC曲线

丙肝发病情况的预测预报研究是一项意义深远的工作，也是流行病学研究的重要课题之一。世界卫生组织2010年5月在一次专家共识研讨会上将HCV的慢性感染作为头等重要的公共卫生问题，所有的医疗当局都被邀请加入到努力预防、识别和快速治疗感染的行动中来^[9]。本研究将丙肝的月发病数划分为4个状态，利用Markov链方法，根据所分状态，预测2009年9—12月丙肝的发病数均>120例，与实际发病数的164、125、145、138例相符。Markov链预测是区间预测，虽然降低了预测的精确度，但却提高了预测的准确度，在含有未知因素和随机性的情况下预测发病数实际值的范围，对防病更具有现实意义。为跟踪数据的发展，以便于直观疾病的发展趋势，本研究同时采用了指数平滑法进行预测，通过观察数据可以发现江苏省丙肝发生病数总体呈现上升趋势，且伴有季节周期性波动，因此选择Holt-Winter季节模型进行拟合和预测。通过比较发现，Holt-Winter季节迭加模型(α=0.46，β=0.001，γ=0.001)预测效果较好，RMSE和MAPE分别为12.629 85和19.18%。指数平滑法在进行预测时可以得到每个月具体的预测发病数，提高了预测的精度。在对疾病进行预警时，本文采用了5年控制图法，通过ROC曲线筛选，发现将P₇₀作为预警界值时预警模型的灵敏度和特异度均>90%。该方法简单易行，可避免不断对参数进行调整的弊端。

由于在发展中国家HCV感染的流行病学并不能很好的描述其特性。即便在建立很好疾病监测系统的国家，急性病报告系统也会低估HCV感染的发病率^[10]。虽然直接测量HCV感染的发病率十分困难，但是仍然可以依赖数学模型推断发病的趋势^[7]。本研究直接用发病数的预测来了解未来丙肝的发病情况，将区间预测与点预测结合，对疾病的发展趋势有更全面的了解，为防控决策提高更可靠更准确的依据。