引用本文

焦辛妮, 王长义, 汪东伟, 刘艳. 基于测量模型结构方程模型GLS与WLS比较[J]. 中国公共卫生, 2015, 31(1): 104-108.

JIAO Xin-ni, WANG Chang-yi, WANG Dong-wei, et al. Comparison of GLS and WLS method based on measurement model of structural equation modeling[J]. Chinese Journal of Public Health, 2015, 31(1): 104-108.

基于测量模型结构方程模型GLS与WLS比较
焦辛妮
1, 王长义
2, 汪东伟
3, 刘艳
1

1. 哈尔滨医科大学卫生统计学教研室, 黑龙江 哈尔滨 150081;
2. 深圳市南山区慢性病防治院;
3. 黑龙江省出入境检验检疫局
数字出版日期:2014-12-4 11:52
基金项目:国家自然科学基金(81172741;30972537)
作者简介:焦辛妮(1988-),女,黑龙江伊春人,硕士在读,研究方向:医学数据的统计分析方法。
通讯联系人:刘艳,E-mail:liuyan@ems.hrbmu.edu.cn
摘要:目的 探讨结构方程模型的广义最小二乘法(GLS)和加权最小二乘法(WLS)2种参数估计方法在不同特征数据中的性能差异。方法 设定包含15个显变量、3个潜变量但未包含内生显变量、内生潜变量的真模型和误设模型,运用SAS 9.1软件的IML模块生成模拟数据,通过CALIS过程进行模型拟合,采用两类错误频率对GLS法和WLS法的性能进行评价。结果 分布特征为正态分布、指数分布和二项分布的数据,在采用相关矩阵和协方差矩阵时,GLS和WLS的两类错误频率均随相关系数或样本含量的增加呈下降趋势;在数据特征相同的条件下,2种矩阵分析均表现为GLS两类错误频率之和小于WLS法;GLS在r=0.3且n≥750即显变量个数的50倍时,或在r=0.5且n≥300即显变量个数的20倍时3种分布的两类错误频率之和均<0.05;WLS相关矩阵分析的结果相对于协方差矩阵分析而言稳定性较差,其协方差矩阵分析表现为不论相关系数如何,只要n≥750即两类错误频率之和<0.05。结论 GLS法和WLS法对参数的估计均为无偏的和渐进有效的,数据条件和矩阵的不同会影响其参数估计结果,在应用过程中应根据实际情况合理选择。
关键词:
结构方程模型
参数估计
广义最小二乘法(GLS)
加权最小二乘法(WLS)
两类错误
Comparison of GLS and WLS method based on measurement model of structural equation modeling
JIAO Xin-ni
1, WANG Chang-yi
2, WANG Dong-wei
3, et al
Department of Health Statistics, School of Public Health, Harbin Medical University, Harbin, Heilongjiang Province 150081, China
Abstract: Objective To investigate the difference in parameter estimation of various datasets between the performances of generalized least squares(GLS) and weighted least squares(WLS)in structural equation modeling(SEM).Methods We set the correlation coefficients between variables and established a true model and misspecified model,which contained 15 variables and 3 latent variables.Using Interactive Matrix Language(IML)module of SAS 9.1 software,we got a simulation of multi-feature data and using Covariance Analysis of Linear Structural Equations(CALIS)procedure we tested the model fit.Then we compared GLS and WLS methods using the frequency of the two types of error as the indicator.Results Whether the distribution of data is normal,exponential or binomial,the relative frequency of the two types of errors shows a downward trend with the increase of the correlation coefficient and the sample size of GLS and WLS when matrix and covariance matrix are used in the analyses.For the data with same characteristics,the sum relative frequency of the two types of errors of GLS is smaller than that of WLS for the analyses with either correlation or covariance matrix.If r=0.3 and n≥750(50 times of significant variable)or r≥0.5 and n≥300(20 times of significant variable),the relative frequency of the two types of error of GLS is less than 0.05 for the data with normal,exponential or binomial distribution.The results of WLS analyses with covariance matrix are more stable than those with correlation matrix and as long as n≥750 the relative frequency of the two types of error is less than 0.05 whatever correlation coefficient is for the analysis with covariance matrix.Conclusion The parameter estimation with both GLS and WLS method is unbiased and asymptotically efficient and the estimation result will be influenced by different data conditions and matrix,indicating the two methods should be selected correctly according to characteristics of the data in the analysis.
Key words:
structural equation model
parameter estimation
generalized least square
weighted least square
two types of error
结构方程模型(structural equation modeling,SEM)是现代统计学重大进展之一,是心理、行为、教育和信息学等强有力的研究工具[1, 2, 3]。常用的结构方程模型参数估计方法有极大似然估计(maximum likelihood estimation,ML)、未加权最小二乘法(unweighted least squares,ULS)、广义最小二乘法(generalized least squares,GLS)、加权最小二乘法(weighted least squares,WLS)、对角加权最小二乘法(diagonal weighted least squares,DWLS)等[4]。GLS法和WLS法是除ML法外应用广泛的SEM参数估计方法,当数据违反多变量正态性假设时,GLS法在使用上有其强韧性[5];而WLS法是一种渐近式分布无干扰的估计方法,不受正态分布假设限制。本研究探讨GLS法和WLS法在不同特征数据参数估计中两类错误发生的频率,对比2种方法的差异,为研究者更加准确运用SEM解决实际问题奠定理论基础和科学依据,也为推广SEM在医学领域中的使用提供方法支持。
1 材料与方法
1.1 材料
运用SAS软件的IML模块,依据因子分析思想设定变量间的相关系数并建立SEM的真模型和误设模型,通过Monte Carlo模拟方法实现多变量多特征数据的模拟。
1.1.1 模型的设定(图 1、2)
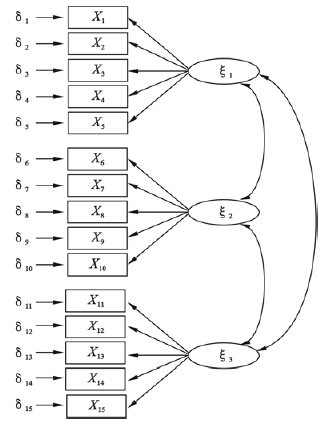
本研究设定了一个未包含内生显变量和内生潜变量的相对简单模型,即测量模型(图 1)。模型中有15个显变量(X1~X15)和3个潜变量(ξ1~ξ3),每个潜变量分别由5个显变量进行测量,构建误设模型时使第6个和第7个显变量(X6和X7)也属于第1个潜变量ξ1(图 2)。
1.1.2 模拟条件的设定(表 1)
主要考虑3个数据特征,即显变量间的相关系数(r)、样本含量(n)和数据分布类型(d),分别采用相关矩阵和协方差矩阵进行参数估计。
1.1.3 拟合效果的评价指标 主要选择RMSEA、NNFI和CFI 3个拟合指数作为判断模型拟合效果的指标,RMSEA<0.10、NNFI>0.90和CFI>0.90表示模型拟合良好。
表 1
 表 1 模拟实验中的参数条件设定情况
|
项目 | 说明
| |
模型(Mo) | Mo1=真模型,Mo2=误设模型
| | 矩阵(Ma) | Ma1=相关矩阵,Ma2=协方差矩阵
| | 相关系数(r) | r1=0.3,r2=0.5,r3=0.7,r4=0.9
| | 分布类型(d) | d1=正态分布,d2=指数分布,d3=二项分布
| | 样本含量(n) | n1=75,n2=150,n3=300,n4=750,n5=1 500
| | 拟合方法(Me) | Me1=GLS,Me2=WLS
|
| 表 1 模拟实验中的参数条件设定情况
|
应用SAS 9.1统计软件,利用CALIS过程进行模型拟合,采用两类错误频率对2种参数估计方法的性能进行评价,其中a表示第一类错误频率,b表示第二类错误频率,a+b表示两类错误频率之和。
2 结 果
2.1 GLS法和WLS法的性能
2.1.1 GLS法(表 2、3)
GLS法对参数的估计是无偏的和渐进有效的,分布特征为正态分布、指数分布和二项分布的数据,在采用相关矩阵和协方差矩阵时,GLS法的两类错误频率均随相关系数或样本含量的增加而减小。当r≥0.5时,n≥300(即显变量个数的20倍)的a+b<0.05;当n≥150时,在相关系数和样本含量相同的条件下,2种矩阵分析均呈正态分布和二项分布的a+b均小于指数分布。
表 2
 表 2 相关矩阵分析时GLS法的两类错误频率
| 数据特征 |
|
n1=75 |
n2=150 |
n3=300 |
n4=750 |
| a |
b |
a+b |
a |
b |
a+b |
a |
b |
a+b |
a |
b |
a+b |
|
正态分布
| | r1=0.3 | 0.198 | 0.552 | 0.750 | 0.162 | 0.128 | 0.290 | 0.098 | 0.000 | 0.098 | 0.002 | 0.000 | 0.002
| | r2=0.5 | 0.166 | 0.370 | 0.536 | 0.116 | 0.006 | 0.122 | 0.030 | 0.000 | 0.030 | 0.000 | 0.000 | 0.000
| | r3=0.7 | 0.134 | 0.240 | 0.374 | 0.094 | 0.000 | 0.094 | 0.006 | 0.000 | 0.006 | 0.000 | 0.000 | 0.000
| | r4=0.9 | 0.104 | 0.132 | 0.236 | 0.092 | 0.000 | 0.092 | 0.008 | 0.000 | 0.008 | 0.000 | 0.000 | 0.000
| | 指数分布
| | r1=0.3 | 0.168 | 0.554 | 0.722 | 0.184 | 0.154 | 0.338 | 0.100 | 0.004 | 0.104 | 0.008 | 0.000 | 0.008
| | r2=0.5 | 0.186 | 0.320 | 0.506 | 0.172 | 0.012 | 0.184 | 0.044 | 0.000 | 0.044 | 0.000 | 0.000 | 0.000
| | r3=0.7 | 0.184 | 0.198 | 0.382 | 0.144 | 0.000 | 0.144 | 0.024 | 0.000 | 0.024 | 0.000 | 0.000 | 0.000
| | r4=0.9 | 0.170 | 0.124 | 0.294 | 0.132 | 0.000 | 0.132 | 0.022 | 0.000 | 0.022 | 0.000 | 0.000 | 0.000
| | 二项分布
| | r1=0.3 | 0.214 | 0.598 | 0.812 | 0.154 | 0.148 | 0.302 | 0.094 | 0.000 | 0.094 | 0.002 | 0.000 | 0.002
| | r2=0.5 | 0.172 | 0.404 | 0.576 | 0.166 | 0.016 | 0.182 | 0.020 | 0.000 | 0.020 | 0.000 | 0.000 | 0.000
| | r3=0.7 | 0.152 | 0.228 | 0.380 | 0.082 | 0.004 | 0.086 | 0.014 | 0.000 | 0.014 | 0.000 | 0.000 | 0.000
| | r4=0.9 | 0.166 | 0.134 | 0.300 | 0.076 | 0.000 | 0.076 | 0.010 | 0.000 | 0.010 | 0.000 | 0.000 | 0.000
|
| 表 2 相关矩阵分析时GLS法的两类错误频率
|
表 3
 表 3 协方差矩阵分析时GLS法的两类错误频率
| 数据特征 |
|
n1=75 |
n2=150 |
n3=300 |
n4=750 |
| a |
b |
a+b |
a |
b |
a+b |
a |
b |
a+b |
a |
b |
a+b |
|
正态分布
| | r1=0.3 | 0.184 | 0.572 | 0.756 | 0.158 | 0.142 | 0.300 | 0.088 | 0.002 | 0.090 | 0.004 | 0.000 | 0.004
| | r2=0.5 | 0.172 | 0.382 | 0.554 | 0.124 | 0.014 | 0.138 | 0.022 | 0.000 | 0.022 | 0.000 | 0.000 | 0.000
| | r3=0.7 | 0.152 | 0.244 | 0.396 | 0.094 | 0.000 | 0.094 | 0.012 | 0.000 | 0.012 | 0.000 | 0.000 | 0.000
| | r4=0.9 | 0.104 | 0.174 | 0.278 | 0.068 | 0.000 | 0.068 | 0.002 | 0.000 | 0.002 | 0.000 | 0.000 | 0.000
| | 指数分布
| | r1=0.3 | 0.170 | 0.532 | 0.702 | 0.206 | 0.168 | 0.374 | 0.124 | 0.002 | 0.126 | 0.004 | 0.000 | 0.004
| | r2=0.5 | 0.186 | 0.366 | 0.552 | 0.138 | 0.012 | 0.150 | 0.038 | 0.000 | 0.038 | 0.000 | 0.000 | 0.000
| | r3=0.7 | 0.186 | 0.202 | 0.388 | 0.152 | 0.000 | 0.152 | 0.012 | 0.000 | 0.012 | 0.000 | 0.000 | 0.000
| | r4=0.9 | 0.182 | 0.122 | 0.304 | 0.130 | 0.000 | 0.130 | 0.024 | 0.000 | 0.024 | 0.000 | 0.000 | 0.000
| | 二项分布
| | r1=0.3 | 0.190 | 0.588 | 0.778 | 0.170 | 0.134 | 0.304 | 0.060 | 0.002 | 0.062 | 0.002 | 0.000 | 0.002
| | r2=0.5 | 0.122 | 0.370 | 0.492 | 0.114 | 0.002 | 0.116 | 0.034 | 0.000 | 0.034 | 0.000 | 0.000 | 0.000
| | r3=0.7 | 0.136 | 0.260 | 0.396 | 0.080 | 0.000 | 0.080 | 0.004 | 0.000 | 0.004 | 0.000 | 0.000 | 0.000
| | r4=0.9 | 0.128 | 0.164 | 0.292 | 0.076 | 0.000 | 0.076 | 0.012 | 0.000 | 0.012 | 0.000 | 0.000 | 0.000
|
| 表 3 协方差矩阵分析时GLS法的两类错误频率
|
WLS法对参数的估计也是无偏的和渐进有效的,虽不要求数据呈多元正态分布,但所需样本含量却较大,故将样本含量分别设定为150、300、750和1 500。当n<300(即显在变量个数的20倍)时采用相关矩阵分析的结果较为理想但a+b较大,3种分布类型数据的b均为0而a相对较大,且a呈现出随相关系数增加而减小的趋势;当n>300时采用协方差矩阵分析的结果较为理想,且当r≥0.5时a+b均<0.05,3种分布类型数据的b也均为0,且a也呈现出相关系数或随样本含量增大而减小的趋势;当n=750(即显在变量个数的50倍)时,除指数分布在r=0.3时a+b略>0.05,其他条件下的a+b均<0.05;当n=1 500(即显在变量个数的100倍)时两类错误已不存在。
表 4
 表 4 相关矩阵分析时WLS法的两类错误频率
| 数据特征 |
|
n2=150 |
n3=300 |
n4=750 |
n5=1500 |
| a |
b |
a+b |
a |
b |
a+b |
a |
b |
a+b |
a |
b |
a+b |
正态分布
| | r1=0.3 | 0.878 | 0.000 | 0.878 | 0.272 | 0.000 | 0.272 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000
| | r2=0.5 | 0.732 | 0.000 | 0.732 | 0.000 | 0.010 | 0.010 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000
| | r3=0.7 | 0.624 | 0.000 | 0.624 | 0.000 | 0.006 | 0.006 | 0.000 | 0.350 | 0.350 | 0.000 | 0.854 | 0.854
| | r4=0.9 | 0.464 | 0.000 | 0.464 | 0.000 | 0.000 | 0.000 | 0.000 | 0.014 | 0.014 | 0.000 | 0.018 | 0.018
| | 指数分布
| | r1=0.3 | 0.980 | 0.000 | 0.980 | 0.470 | 0.000 | 0.470 | 0.004 | 0.000 | 0.004 | 0.000 | 0.000 | 0.000
| | r2=0.5 | 0.948 | 0.000 | 0.948 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000
| | r3=0.7 | 0.856 | 0.000 | 0.856 | 0.000 | 0.000 | 0.000 | 0.000 | 0.056 | 0.056 | 0.000 | 0.004 | 0.004
| | r4=0.9 | 0.476 | 0.000 | 0.476 | 0.000 | 0.012 | 0.012 | 0.000 | 0.042 | 0.042 | 0.000 | 0.098 | 0.098
| | 二项分布
| | r1=0.3 | 0.876 | 0.000 | 0.876 | 0.284 | 0.000 | 0.284 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000
| | r2=0.5 | 0.744 | 0.000 | 0.744 | 0.000 | 0.016 | 0.016 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000
| | r3=0.7 | 0.636 | 0.000 | 0.636 | 0.000 | 0.014 | 0.014 | 0.000 | 0.376 | 0.376 | 0.000 | 0.874 | 0.874
| | r4=0.9 | 0.466 | 0.000 | 0.466 | 0.000 | 0.002 | 0.002 | 0.000 | 0.018 | 0.018 | 0.000 | 0.026 | 0.026
|
| 表 4 相关矩阵分析时WLS法的两类错误频率
|
表 5
 表 5 协方差矩阵分析时WLS法的两类错误频率
| 数据特征 |
|
n2=150 |
n3=300 |
n4=750 |
n5=1500 |
| a |
b |
a+b |
a |
b |
a+b |
a |
b |
a+b |
a |
b |
a+b |
|
正态分布
| | r1=0.3 | 0.984 | 0.000 | 0.984 | 0.686 | 0.000 | 0.686 | 0.014 | 0.000 | 0.014 | 0.000 | 0.000 | 0.000
| | r2=0.5 | 0.946 | 0.000 | 0.946 | 0.468 | 0.000 | 0.468 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000
| | r3=0.7 | 0.932 | 0.000 | 0.932 | 0.286 | 0.000 | 0.286 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000
| | r4=0.9 | 0.904 | 0.000 | 0.904 | 0.212 | 0.000 | 0.212 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000
| | 指数分布
| | r1=0.3 | 0.984 | 0.000 | 0.984 | 0.700 | 0.000 | 0.700 | 0.068 | 0.000 | 0.068 | 0.000 | 0.000 | 0.000
| | r2=0.5 | 0.966 | 0.000 | 0.966 | 0.590 | 0.000 | 0.590 | 0.018 | 0.000 | 0.018 | 0.000 | 0.000 | 0.000
| | r3=0.7 | 0.946 | 0.000 | 0.946 | 0.608 | 0.000 | 0.608 | 0.022 | 0.000 | 0.022 | 0.000 | 0.000 | 0.000
| | r4=0.9 | 0.958 | 0.000 | 0.958 | 0.658 | 0.000 | 0.658 | 0.034 | 0.000 | 0.034 | 0.000 | 0.000 | 0.000
| | 二项分布
| | r1=0.3 | 0.986 | 0.000 | 0.986 | 0.648 | 0.000 | 0.648 | 0.018 | 0.000 | 0.018 | 0.000 | 0.000 | 0.000
| | r2=0.5 | 0.936 | 0.000 | 0.936 | 0.450 | 0.000 | 0.450 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000
| | r3=0.7 | 0.930 | 0.000 | 0.930 | 0.342 | 0.000 | 0.342 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000
| | r4=0.9 | 0.896 | 0.000 | 0.896 | 0.220 | 0.000 | 0.220 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000
|
| 表 5 协方差矩阵分析时WLS法的两类错误频率
|
真模型共需要估计33个参数,其中包括15个显变量的因子负荷、15个误差方差和3个因子(即3个潜变量)间的相关系数,自由度为87。结果显示各显变量的路径系数均>0.4,且t值均>2(而t0.05/2,87=1.987 6),差异有统计学意义(P<0.05),但因子间的相关系数则差异无统计学意义(P>0.05);RMSEA=0、NNFI=1.16和CFI=1.00,3种拟合指数均在可接受范围内,提示模型拟合效果良好。
表 6
 表 6 SAS-CALIS过程计算出的真模型参数估计值
| 变量 |
路径系数 |
误差方差 |
| b |
Sb |
t |
e |
Se |
t |
| X1 | 0.58 | 0.07 | 8.87 | 0.62 | 0.07 | 8.90
| | X2 | 0.56 | 0.07 | 8.21 | 0.72 | 0.07 | 9.65
| | X3 | 0.52 | 0.07 | 7.81 | 0.68 | 0.07 | 9.51
| | X4 | 0.49 | 0.07 | 7.43 | 0.69 | 0.07 | 9.64
| | X5 | 0.56 | 0.06 | 8.86 | 0.58 | 0.07 | 8.93
| | X6 | 0.68 | 0.07 | 10.02 | 0.55 | 0.07 | 7.36
| | X7 | 0.56 | 0.06 | 8.84 | 0.56 | 0.06 | 8.76
| | X8 | 0.56 | 0.07 | 8.18 | 0.73 | 0.08 | 9.47
| | X9 | 0.38 | 0.06 | 5.96 | 0.70 | 0.06 | 10.76
| | X10 | 0.43 | 0.06 | 6.73 | 0.69 | 0.07 | 10.60
| | X11 | 0.63 | 0.07 | 8.89 | 0.69 | 0.08 | 8.42
| | X12 | 0.50 | 0.06 | 8.18 | 0.55 | 0.06 | 9.23
| | X13 | 0.54 | 0.06 | 8.59 | 0.56 | 0.06 | 8.91
| | X14 | 0.43 | 0.07 | 6.25 | 0.81 | 0.08 | 10.58
| | X15 | 0.47 | 0.06 | 7.38 | 0.62 | 0.06 | 9.77
| | f1 | -0.01a | 0.09 | -0.10 | 1.00 |
| | f2 | 0.05b | 0.09 | 0.54 | 1.00 |
| | f3 | 0.13c | 0.09 | 1.56 | 1.00 |
| | | 注:a表示因子f1与f2之间的相关系数;b表示f2与f3之间的相关系数;c表示f1与f3之间的相关系数。 |
| 表 6 SAS-CALIS过程计算出的真模型参数估计值
|
目前,评价SEM比较公认的标准是相对指数≥0.90的拟合模型可以接受,RMSEA<0.05表示模型拟合好,RESEA在0.05~0.10表示模型可以接受[6];一个适当的拟合指数应具有不受样本含量影响和对误设模型有敏感性的特征[7]。为此,本研究主要通过3个拟合指数(RESEA、NNFI和CFI)对结构方程的参数拟合进行评价[8],设定模型的RMSEA<0.01、NNFI=1.16和CFI=1.00,说明设定模型拟合良好。
ML法估计参数要求样本数据符合多变量正态性假设,样本数也不能太少[9],故正态分布数据在大样本时,采用ML法估计参数得到的结果均是适当可信且正确的。有研究认为,在违反正态分布假设时最好使用含有加权式估计程序的方法,如WLS法[10];也有资料显示,如果数据为大样本,但观察数据不符合多变量正态性假设时最好采用GLS估计法[5]。本研究设定了一个未包含内生显变量和内生潜变量的相对简单模型(测量模型),模拟实验结果显示,无论数据的分布特征为正态分布、指数分布和二项分布,无论是采用相关矩阵还是协方差矩阵,GLS法的两类错误频率均随相关系数或样本含量的增加而减小,GLS法确实呈现出结论可靠的优点;WLS法相关矩阵分析的结果相对于协方差矩阵分析而言稳定性较差,WLS法在进行相关矩阵分析时呈现出随样本含量增大或相关系数增加第二类错误频率及两类错误频率之和有波动现象,可能与WLS法采用高阶加权矩阵有关(WLS法权重矩阵估计所需样本量计算在观察变量的数量k≤12时至少为200,在k>12时至少为1.5k(k+1)[11]),WLS法在观察变量数量较大时需要有很大的样本量来估计其权重矩阵且计算耗时[12],若样本量不足会产生很大偏度,从而导致WLS法的权重不可逆;在数据特征相同的条件下,GLS法两类错误频率之和小于WLS法。
本研究只考虑了SEM的测量模型,数据特征也只考虑了3种分布类型、4个相关系数和5个样本含量,在后续研究中应增大模型的复杂程度,对全模型进行研究,完善对数据特征的设定,再对比GLS法和WLS法参数估计的性能差异。
参考文献
| [1] |
Anderson JC,Gerbin DW.Structural equation modeling in practice:a review and recommended two-step approach[J].Psychological Bulletin,1998,103(3):411-423.
|
| [2] |
欧凤荣,丁海龙,高双,等.城市贫困人群生命质量影响因素结构方程模型[J].中国公共卫生,2012,28(6):867-868.
|
| [3] |
张鹏,楼超华,高尔生.未婚青少年性行为影响因素结构方程模型分析[J].中国公共卫生,2012,28(3):399-400.
|
| [4] |
张岩波.潜变量分析[M].北京:高等教育出版社,2009:91-93.
|
| [5] |
吴明隆.结构方程模型-AMOS的操作与应用[M].重庆:重庆大学出版社,2009:24-27.
|
| [6] |
王济川,王小倩,姜宝法.结构方程模型:方法与应用[M].北京:高等教育出版社,2011:16-23.
|
| [7] |
王长义,王大鹏,赵晓雯,等.结构方程模型拟合指数的比较[J].现代预防医学,2010,37(1):7-9.
|
| [8] |
温忠麟,侯杰泰,马什赫伯特.结构方程模型检验:拟合指数与卡方准则[J].心理学报,2004,36(2):186-194.
|
| [9] |
黄芳铭.结构方程模式:理论与应用[M].北京:中国税务出版社,2005:121-124.
|
| [10] |
方敏,黄正峰.结构方程模型下非正态数据的处理[J].中国卫生统计,2010,27(1):84-87.
|
| [11] |
Sörbom D.Model modification[J].Psychometrika,1989,54(3):371-384.
|
| [12] |
Bentler PM,Yuan KH.Structural equation modeling with small samples:test statistics[J].Multivariate Behavioral Research,1999,34(2):181-197.
|

 2015, Vol. 31
2015, Vol. 31


