时间序列是指观察或记录到的一组按时间顺序排列的数据。由于时间序列展示了研究对象在一定时期内的发展变化过程,因此可以从中分析寻找出其变化特征、趋势和发展规律的需要信息。时间序列预测实质上就是根据现在与过去的随机序列的样本取值,对未来某一个时刻的随机变量进行估计〔1〕。时间序列分析是专门用于分析这种时间序列资料的统计模型,它主要分析的是变量间的因果关系,重点观察变量随时间变化的发展规律〔2〕。时间序列分析方法可以分成两大类: 时域和频域,前者将时间序列看成是过去一些点的函数,具有随时间系统变化的趋势,可以用参数来加以描述,并可通过差分、周期等还原成随机序列,而后者认为时间序列是由数个正弦波成份叠加而成〔2〕。本研究利用吉林省腮腺炎监测系统2004-2010 年的月发病数据,建立腮腺炎疫情时间序列模型(autoregressive integrated moving average model,ARIMA) 进行腮腺炎疫情的预测和预警,现将结果报告如下。
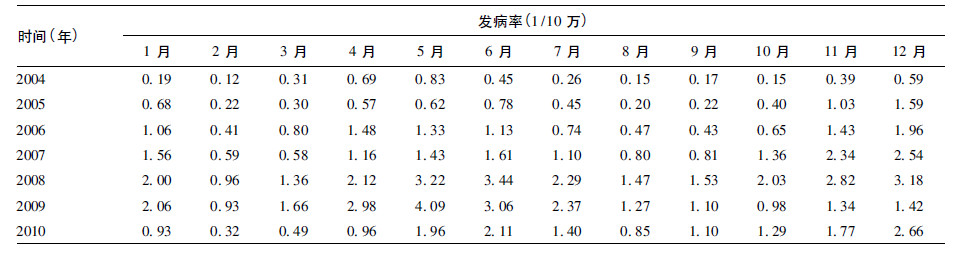
材料与方法(1) 资料来源: 疫情资料来源于吉林省腮腺炎监测系统数据库,人口资料来源于同时期的统计年鉴,吉林省2004-2010 年腮腺炎月发病率见表 1。(2) 统计分析: 利用SPSS 15.0 统计软件ARIMA 分析方法,通过数据处理及模型识别、模型检验和产生预测等步骤对吉林省2004-2010 年腮腺炎月发病数时间序列进行分析。ARIMA 模型见文献〔2, 3〕。
| 表 1 吉林省2004-2010 年腮腺炎月发病率 |
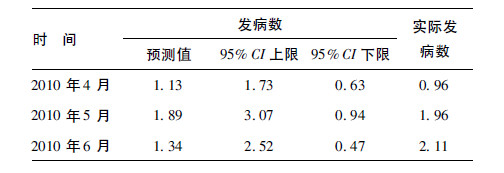
(1) 数据处理及模型建立: 根据平方根转换后月发病率,绘制自相关函数和偏自相关函数图,与ARIMA 模型自相关分析标准图进行对照,可以初步确定此序列符合 RIMA(3,1,1) (0,1,0) s 模型。模型适合度统计量采用 Ljung-Box 方法,模型符合较好(P = 0.37) 。(2) 模型检验: 利用所建模型,得到实际值与预测值之差即残差,计算残差相关系数,如果模型合适,则残差应是一随机序列。对残差进行自相关和偏自相关分析表明,自相关系数均未超出± 0.5,因此不能认为残差序列各数值间有相关性。(3) 产生预测(表 2) : 根据以上模型,对2010 年4 月至6 月份的发病进行预测。 结果表明,实际发生病例数与预测发生的病例数比较吻合,实际发病率均在预测值的95%可信区间内。
| 表 2 ARIMA 模型预测值 |
流行性腮腺炎是一种在全球范围内广泛流行的急性呼吸道传染病,多发于儿童和青少年,至今尚缺乏特效抗病毒药物治疗,可累及各腮体组织和脏器,严重者可导致伤残或死亡; 经常在中小学和托幼机构引起爆发。2009 年吉林省传染病监测系统报告腮腺炎6 357 例,发病率为23.25 /10 万,腮腺炎发病数排法定传染病前5 位,全省报告流行性腮腺炎突发公共卫生事件4 起,占传染病类突发事件1.83%。利用时间序列模型的技术,建立腮腺炎疫情时间序列模型,对及早控制腮腺炎非常必要。ARIMA 模型在国内外被广泛应用于很多领域中,利用ARIMA 模型,澳大利亚分析了罗斯河病毒发病率与气候变化的关系〔4〕,美国对2010 年人群平均寿命的预测〔5〕。我国在公路、商品销售等方面均利用ARIMA 模型进行了预测〔6〕,在医学领域中ARIMA 被用于月门诊量、脑卒中发病的预测〔7, 8〕和艾滋病发病趋势预测〔9〕。吉林省2004-2010 年腮腺炎月实际发病对数曲线与腮腺炎拟合发病对数曲线拟合度较好,所建立的腮腺炎疫情预测数学模型科学可信,为腮腺炎预测预警增加一个全新的预测方式和技术手段,使腮腺炎疫情预测预警更加科学、准确。对于腮腺炎预防控制,在继续实施现行免疫策略的情况下,此模型可用于一定时期的预测预警。但是,一旦改变免疫策略,势必改变流行规律,则应考虑建立新的腮腺炎疫情ARIMA 模型和预测预警方法。腮腺炎是通过疫苗可预防的传染病,而且通过在爆发地区开展有效的应急接种可以控制疫情蔓延和流行。建立腮腺 炎疫情ARIMA 模型可对未来几个月腮腺炎的发病进行精确的预测,这对提前发现腮腺炎疫情,提出预警并制定相应的预防控制策略措施提供了依据。
| 〔1〕 | 王春平,王志锋,单杰,等.随机时间序列分析法在传染病预测中的应用[J].中国医院统计,2006,13(3):229-232. |
| 〔2〕 | 田鑫,陈超,周剑惠,等,应用时间序列模型预测麻疹疫情及其应用[J].中国疫苗与免疫,2008,4(4):4-7. |
| 〔3〕 | Box GEP,Jenkins GM,Reinsel GC.Time series analysis:forecasting and control third edition[N].New Jersey:Prentice Hall,1994. |
| 〔4〕 | Tong SL,Hu WB.Climate variation and incidence of Ross River virus in Cairns,Australia:a time-series analysis[J].Environmental Health Perspectives,2001,109(12),1271-1273. |
| 〔5〕 | Levine RS,Foster JE,Fullilove RE,et al.Black-white inequalities in mortality and life expectancy,1933-1999:implications for healthy people 2010[J].Public Health Reports,2001,116:474-483. |
| 〔6〕 | 陈文华,边浩毅,王怡民,等.基于ARIMA模型的公路客运量预测[J].重庆工商大学学报,2006,16(5):95-97. |
| 〔7〕 | 梁桂玲,刘颜,邓泗沐.ARIMA模型应用于月门诊量预测[J].中国医院统计,2006,13(1):24-26. |
| 〔8〕 | 程锦泉,刘建平,张仁利,等.深圳市脑卒中发病与气温关系[J].中国公共卫生,2007,23(8):970-971. |
| 〔9〕 | 冯超,白杉.时间序列模型拟合艾滋病发病趋势预测[J].中国公共卫生,2005,21(7):893-893. |
 2012, Vol. 28
2012, Vol. 28