中国公共卫生  2009, Vol. 25 Issue (9): 1102-1104   PDF    
引用本文
郑辉烈, 王忠旭, 王增珍. Poisson及负二项分布对微核试验数据拟合效果[J]. 中国公共卫生, 2009, 25(9): 1102-1104.
ZHENG Hui-lie, WANG Zhong-xu, WANG Zeng-zhen Poisson distributon and negative binomial distribution fitting for data of cytokinesis-block micronucleus test[J]. Chinese Journal of Public Health, 2009, 25(9): 1102-1104.
Poisson及负二项分布对微核试验数据拟合效果
郑辉烈1,2, 王忠旭3, 王增珍1     
1. 华中科技大学同济医学院公共卫生学院流行病与卫生统计系, 武汉 430030;
2. 南昌大学医学院公共卫生学院流行病与卫生统计学系;
3. 中国疾病预防控制中心
收稿日期: 2008-12-24
基金项目: 国家科技部“973”课题(2002CB512910)
作者简介: 郑辉烈(1976-), 男, 江西上饶人, 博士在读, 主要从事统计方法在医学中的应用研究。
通讯作者: 王增珍
摘要: 目的 探讨微核试验数据(每1000个双核淋巴细胞中具有微核的淋巴细胞数)的统计分布, 为微核试验数据的统计分析提供依据. 方法 利用东北某大型钢铁公司158名焦炉工和66名非焦炉工微核检测的实例数据, 进行矩法估计Poisson分布和二项分布的参数, 同时拟合Poisson分布和负二项分布, 比较其拟合效果. 结果 拟合优度检验显示, 焦炉工和非焦炉工微核数据均不服从Poisson分布(P < 0.001);焦炉工微核数据服从负二项分布(P=0.545), 非焦炉工微核数据虽不服从负二项分布(P < 0.001), 但该数据似合负二项分布的效果要好于拟合Poisson分布(拟合负二项分布比值3.1 < 拟合Poisson分布比值20.3). 结论 对于具有聚集性趋向(即方差与均数比值较大)的微核数据, 相对于拟合Poisson分布, 拟合负二项分布是一较好选择.
关键词： 微核     Poisson分布     负二项分布     似合优度    
Poisson distributon and negative binomial distribution fitting for data of cytokinesis-block micronucleus test
ZHENG Hui-lie, WANG Zhong-xu, WANG Zeng-zhen     
Department of Epidemiology and Statistics, School of Public Health, Tongji Medical Colldge of Huazhong University of Science and Technology, Wuban 430030, China
Abstract: Objective To investigate the statistical distribution of the data of cytok inesis-block micronucleus test to provide basis of statistical analysis. Methods The moment estimate parameters of the Poisson distribution, the negative binomial distribution, and Pearson goodness of fit test were used to evaluate the goodness of fit of the two different distributions. Results Neither the data of cytokines is-block mucronuc leustest for coke-oven workers and non-coke-oven workers presen ted Poisson distribution (P < 0.001).The data of coke-oven workers showed a negative binomial distribution (P=0.545) and the data of non-coke-oven workes did not (P < 0.001). Conclusion For the data of cytokinesis-block micro-nucleus test with cluste red characte ristics, the negative binomial distribution fitting was a better choice compared to the Poissond is tribution fitting.
Key words: micronucleus     Poisson distrbution     negative binomial distrbution     the goodness of fit test    

微核试验是一种检测细胞内染色体畸变的方法, 常以一定数量的细胞(1000个)进行微核计数为观察指标〔1〕, 因此, 微核数据往往不服从正态分布〔2〕。对于微核数据的处理分析, 通常采用非参数统计方法或变量变换后再进行统计处理〔3-4〕。但从利用微核数据信息的角度考虑, 直接利用微核试验数据的统计分布建立相应的模型〔5〕更为合适, 前提条件是微核试验数据的统计分布已知。本文以东北某钢厂焦炉工和非焦炉工的微核检测数据为例, 采用矩法估计Poisson分布参数(λ)及负二项分布的参数(μ, k), 并进行拟合优度检验, 并比较这2种分布对微核数据的拟合效果, 为微核数据的统计分析提供依据。

1 对象与方法 1.1 对象

东北某大型钢铁公司同一焦炉作业的158名焦炉工和无明显工作相关的多环芳烃(PAHs)及射线暴露的66名非焦炉工为调查对象, 平均年龄分别为(40.0±7.7)岁, (38.1±7.9)岁, 差异无统计学意义。2组均以男性占多数, 其中焦炉工男性占91.1%;非焦炉工男性占86.4%, 性别构成差异无统计学意义。

1.2 方法

抽取所有调查对象1 mL肘静脉血进行双核淋巴细胞微核(cytokinesi-blockmicronucleus, CBMN)试验〔1〕。以计数1 000个双核淋巴细胞中含1个或1个以上的微核细胞数为观察指标, 评价个体外周血淋巴细胞染色体损伤的情况。

1.3 统计分析

Poisson分布和负二项分布均是离散型分布, Poisson分布由其均数即λ参数决定, 且其方差与均数相等, 用于描述单位时间或空间内稀有事件发生数的概率分布, 要求被描述的单位时间或空间内稀有事件的发生是相互独立的, 即事件间没有聚集性; 负二项分布由均数(μ)和聚集性指数(k)2个参数决定, 其方差与均数的比值较大, 则k值越小, 即k是刻画负二项分布变量的离散程度也即聚集性程度的参数。本次研究采用矩法估计Poisson分布和负二项分布的参数, 对于方差与均数比值较大, 即可能存在聚集性趋向的微核试验数据, 先按Poisson分布拟合, 再拟合负二项分布, 并进行Poisson拟合优度检验, 检验水准为0.1。所有数据分析均在Stata 8.0软件中完成。

2 结果 2.1 微核数据的基本特征

焦炉工组和非焦炉工组的微核淋巴细胞数(微核淋巴细胞数/1000个双核淋巴细胞)的均数分别为9.3, 4.0;方差分别为44.1, 12.9;方差与均数之比值为别为4, 7, 3.2, 即变异程度, 相对于其均数而言, 2组人群相差较小。但2组人群微核淋巴细胞数方差与均数之比值均> 1, 反映微核淋巴细胞的出现具有一定的聚集性趋向。

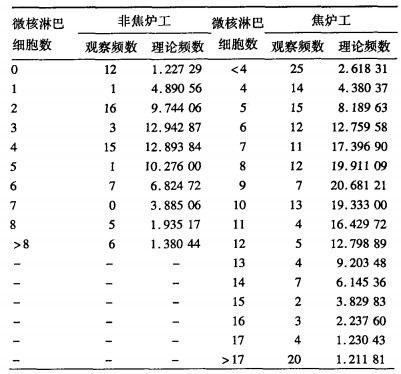
2.2 Poisson分布拟合结果(表 1)
表 1 Poisson分布对微核数据的拟合结果

矩法估计非焦炉工组和焦炉工组微核数据Poisson分布λ参数分别为4.0, 9.3。由于理论频数较小, 非焦炉工组微核淋巴细胞数最后组段的频数进行合并处理, 焦炉工组的前4个组段(0, 1, 2, 3)和最后组段的频数也分别进行合并。经Poisson拟合优度检验结果显示, 非焦炉工(χ2=142.23, v=7, P < 0.001)和焦炉工(χ2=550.4, v=13, P < 0.001)2组人群的微核淋巴细胞数均不服从Poisson分布。

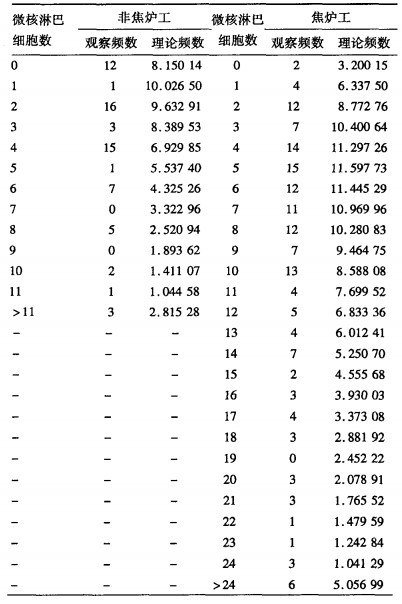
2.3 负二项分布拟合结果(表 2)
表 2 负二项分布微核数据的拟合结果

矩法估计非焦炉工组和焦炉工组负二项分布参数, 分别为μ=4.0, k=1.78;μ=9.3, k=2.51。由于理论频数较小, 分别对2组微核淋巴细胞数的最后组段的频数进行合并。拟合结果表明, 焦炉工组微核淋巴细胞数服从负二项分布(χ2=21.58, v=23, P=0.545), 非焦炉工组数据不服从负二项分布(χ2=40.30, v=13, P < 0.00 1)。

2.4 拟合结果比较(图 1, 2)
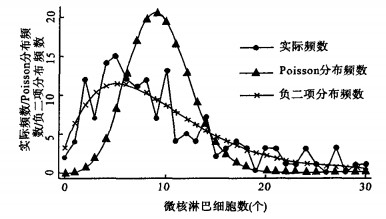
图 1 非焦炉工微核数据实际频数、Poisson分布和负二项分布理论频数比较

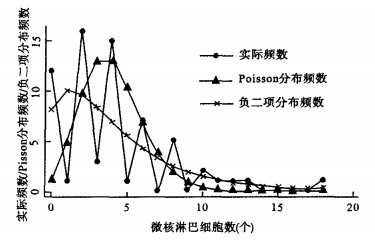
图 2 焦炉工微核数据实际频数、Poisson分布和负二项分布理论频数比较

拟合优度检验结果表明, 非焦炉工组微核数据既不服从Poisson分布也不服从负二项分布。从拟合优度值与其自由度的比值大小来看, 该数据拟合负二项分布的效果好于拟合Poisson分布(拟合负二项分布的比值3.1 < 拟合Poisson分布比值20.3)。从图 1可见, 非焦炉工组微核数据实际频数、Poisson分布和负二项分布理论频数吻合程度较差, 大部分负二项分布理论频数大小介于Poisson分布和实际频数之间, 这一现象也表明, 非焦炉工组微核数据负二项分布的拟合效果相对较好。对于焦炉工组微核淋巴细胞数, 拟合优度检验结果表明, 该微核数据资料服从负二项分布, 不服从Poisson分布。图 2显示, 负二项分布理论频数与微核淋巴细胞数实际频数吻合较好, 而Poisson分布理论频数与实际频数相差较明显。

3 讨论

近年来, 有研究利用微核数据建立Poisson回归或负二项回归模型来分析微该与相关因素的关系〔5-8〕, 但是, 建立Poisson回归或负二项回归模型的前提是微核数据必须服从或近似服从Poisson分布或负二项分布。本研究结果显示, 焦炉工和焦炉工的微核试验数据的方差与均数之比值均> 1, 反映数据存在一定程度的聚集性趋向, 提示微核试验数据可能不符合Poisson分布, 这与拟合优度检验结果相一致。本次研究中, 2组工人微核试验数据的统计分布不一致, 即焦炉工微核数据服从负二项分布, 而非焦炉工微核数据不服从。可能是由于非焦炉工与焦炉工组间均衡性差, 非焦炉工组样本量较小等原因引起, 有待进一步研究分析。但对于非焦炉工人群, 相对于拟合Poisson分布, 微核数据拟合负二项分布是一种较好的选择, 这可能是源于微核淋巴细胞数不具完全的独立性, 具有其种聚集性趋向所致。本研究结果提示, 相对于拟合Poisson分布模型, 对微核试验数据拟合负二项分布模型效果更好。

参考文献
[1] Fenech M. The in vitro micronucleus technique[J]. Mutat Res, 2000, 455 : 81–95. DOI:10.1016/S0027-5107(00)00065-8
[2] 陈少华. 人外周血淋巴细胞微核的频数分布[J]. 癌变·畸变·突变, 1994, 6(4) : 37–40.
[3] 唐萌, 叶明宪, 袁震华, 等. 八氯二丙醚暴露工人微核及DNA损伤程度[J]. 中国公共卫生, 2006, 22(9) : 1082–1083.
[4] 刘楠, 崔涛, 孟会林, 等. MTHFR基因多态性与1, 3-丁二烯作业工人染色体损伤的关系[J]. 毒理学杂志, 2008, 22(2) : 84–87.
[5] Mateuca RA, Roelants M, Larmarcovai G, et al. hOGGI (326), XRCCand XRCC3(241) polymorphisms influence micronucleus in human lymphocytes in vivo[J]. Mutagenesis, 2008, 23(1) : 35–41.
[6] Pastor S, Gutierrez S, Creus A, et al. Cytogenetic analysis of Greek farmers using the micronucleus assay in peripheral lymphocytes and buccal cells[J]. Mutagenesis, 2001, 16(6) : 539–545. DOI:10.1093/mutage/16.6.539
[7] Pastor S, Gutierrez S, Creus A, et al. Micronuclei in peripheral blood lymphocytes and buccal epithelial cells of Polish farmers exposed to pesticides[J]. Mutat Res, 2001, 4959(1-2) : 147–156.
[8] Kirsch-Volders M, Micheline RA, Mateuca M, et al. The effects of GSTM1 and GSTT1 pllymorphisms on micronucleus frequencies in human lymphocytes in vivo[J]. Cancer Epidemiol Biomarkers prey, 2006, 15(5) : 1038–1042. DOI:10.1158/1055-9965.EPI-05-0487