低本底α、β测量仪和流气正比计数器总α、总β测量仪主要用于对样品中α、β放射性进行实验室分析。二者的探测原理不同,但都采用类似的样品盘和铺样方式,在对其计量过程中需要使用标准平面源。使用平面源对仪器进行计量时,结构简图如图1。
|
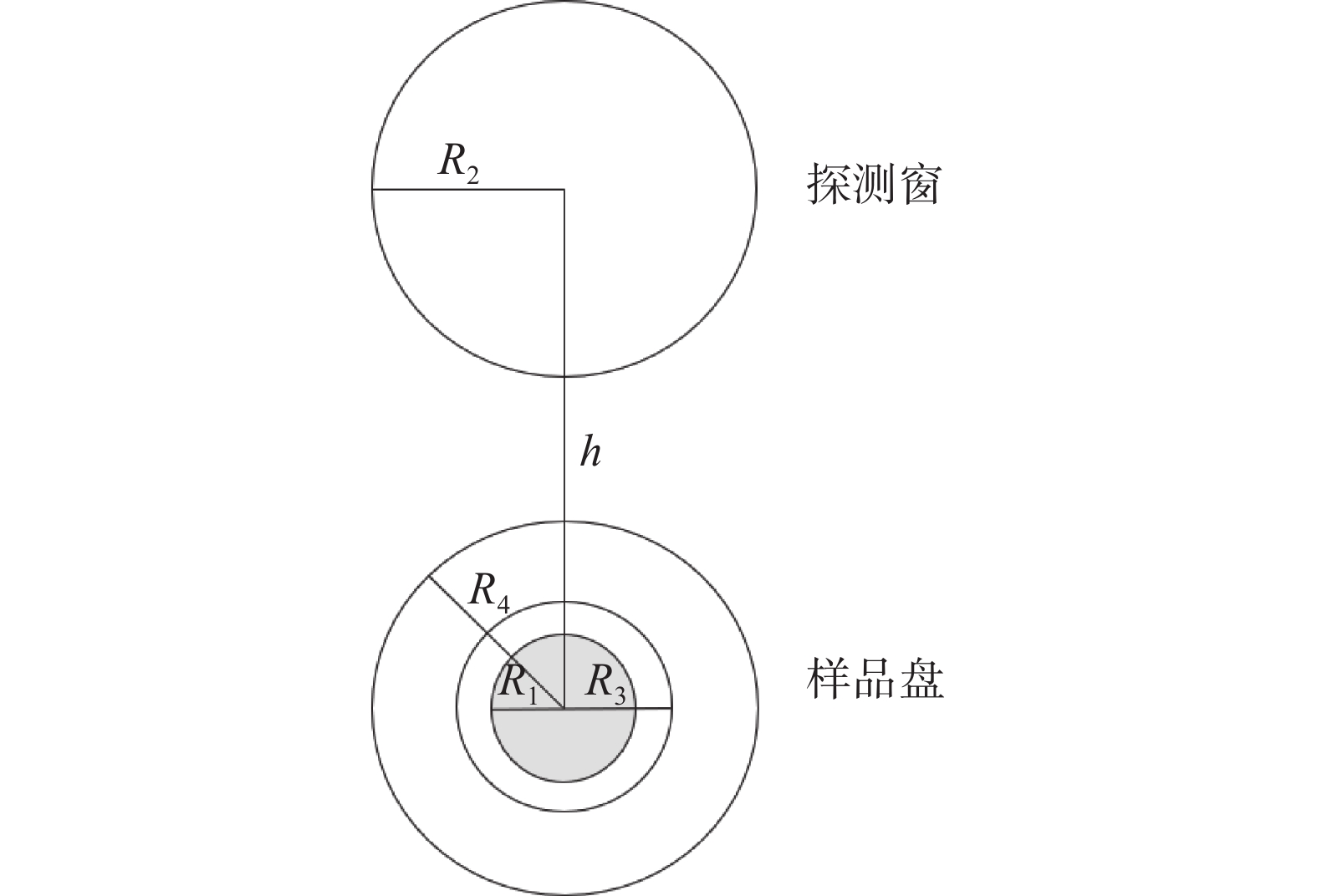
图 1 使用标准平面源计量仪器简图 Figure 1 Schematic of a metering instrument with a standard planar source |
平面源在进行量值传递的时候,与探测器之间会因为探测器半径R2、样品盘的半径R4、源的半径R3、活性区半径R1以及探测窗平面与源表面的距离h等几何结构形成立体角,从探测器表面发射的粒子并非全部都能进入到探测窗,探测器对源所张立体角会影响到这些粒子的数目,进而会影响到最终的探测效率,由立体角引入的效率影响因子本文称为几何因子,Ruffle[1]、Ruby等[2],Gardner等[3]以及倪光炯等[4]研究了面源与探测器同轴平行时的几何因子的计算方法,Conway[5]在前人研究基础上研究了几何因子在非同轴4π球面度情况下以及非圆面源情况下的的计算方法,刘宗良等[6]使用蒙特卡罗方法研究了圆面源与圆面探测器非平行时的几何因子。实验室操作仪器时,变量主要是平面源的活性区半径以及活性区圆心与探测窗圆心的错位间距,因此本文着重讨论平行同轴情况下活性区半径对几何因子的影响以及平行非同轴情况下间距对几何因子的影响。
1 材料与方法Conway的研究给出了在探测器与圆形平面源之间呈4π球面度时计算几何因子的方式,由于平面源一般是以2π球面度的表面发射率进行溯源,所以本文讨论特指2π球面度,而平行非同轴情况下2π球面度的几何因子可表示为
| $ G = \frac{2{R}_{2}}{{R}_{1}}{\int }_{0}^{\infty }\frac{{J}_{0}\left(sa\right){J}_{1}\left(s{R}_{2}\right){J}_{1}\left(s{R}_{1}\right)}{s}{e}^{-sh}ds $ | (1) |
式中G为几何因子;R2为探测器窗半径(mm);R1为面源活性区半径(mm);h为源表面与探测窗平面的垂直距离(mm);a为面源圆心与探测窗圆心水平方向间距(mm),如图2所示,当a = 0 mm时,二者圆心是正对的。

|
图 2 间距a示意图 Figure 2 Schematic of the distance a |
对于安装就位的仪器而言,距离h以及探测窗的半径R2一般是固定不变的,而源半径R3、活性区半径R1(本论文中活性区的圆心与平面源的圆心是重合的)以及间距a可能会变化,其中a可在[0, R4−R3]之间变化。
1.1 活性区半径的变化对几何因子的影响现行有效的检定规程[7-8]中给出了标准平面源的活性区半径的范围为[9,12.5] mm,如果在平行同轴即a = 0 mm且R2 = 22.5 mm,h = 2 mm的条件下,仅改变R1值,利用MATLAB和公式(1)计算得到G值如表1。
|
|
表 1 G值随R1值的变化 Table 1 The change in G value with R1 value |
|
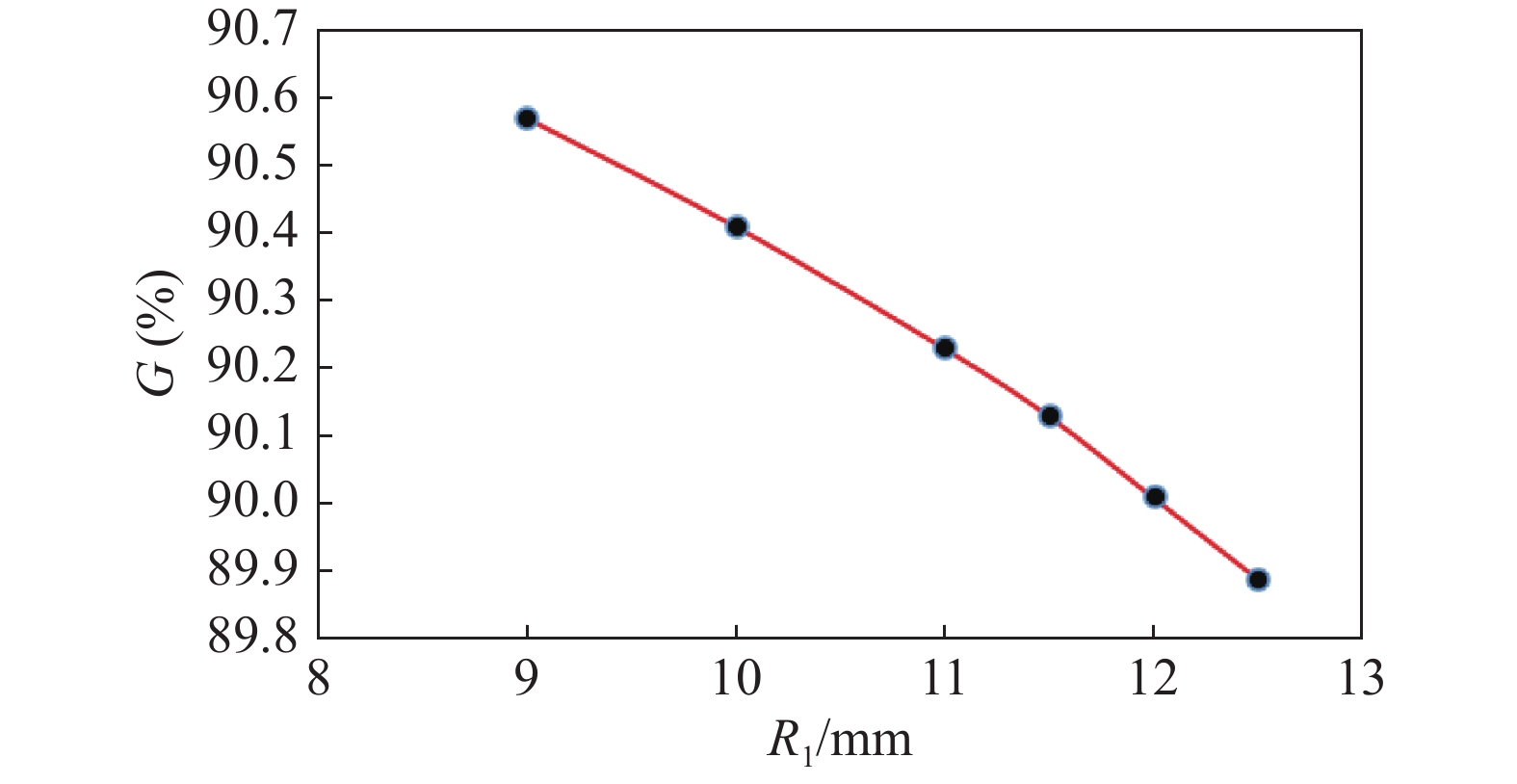
图 3 G值随R1值的变化情况 Figure 3 The change in G value with R1value |
表1和图3均显示,保持其他条件不变,几何因子随着标准源活性区半径的减小而单调增大。也就是说,表面发射率相同的情况下,活性区越小,发射到探测窗内的放射性粒子越多。
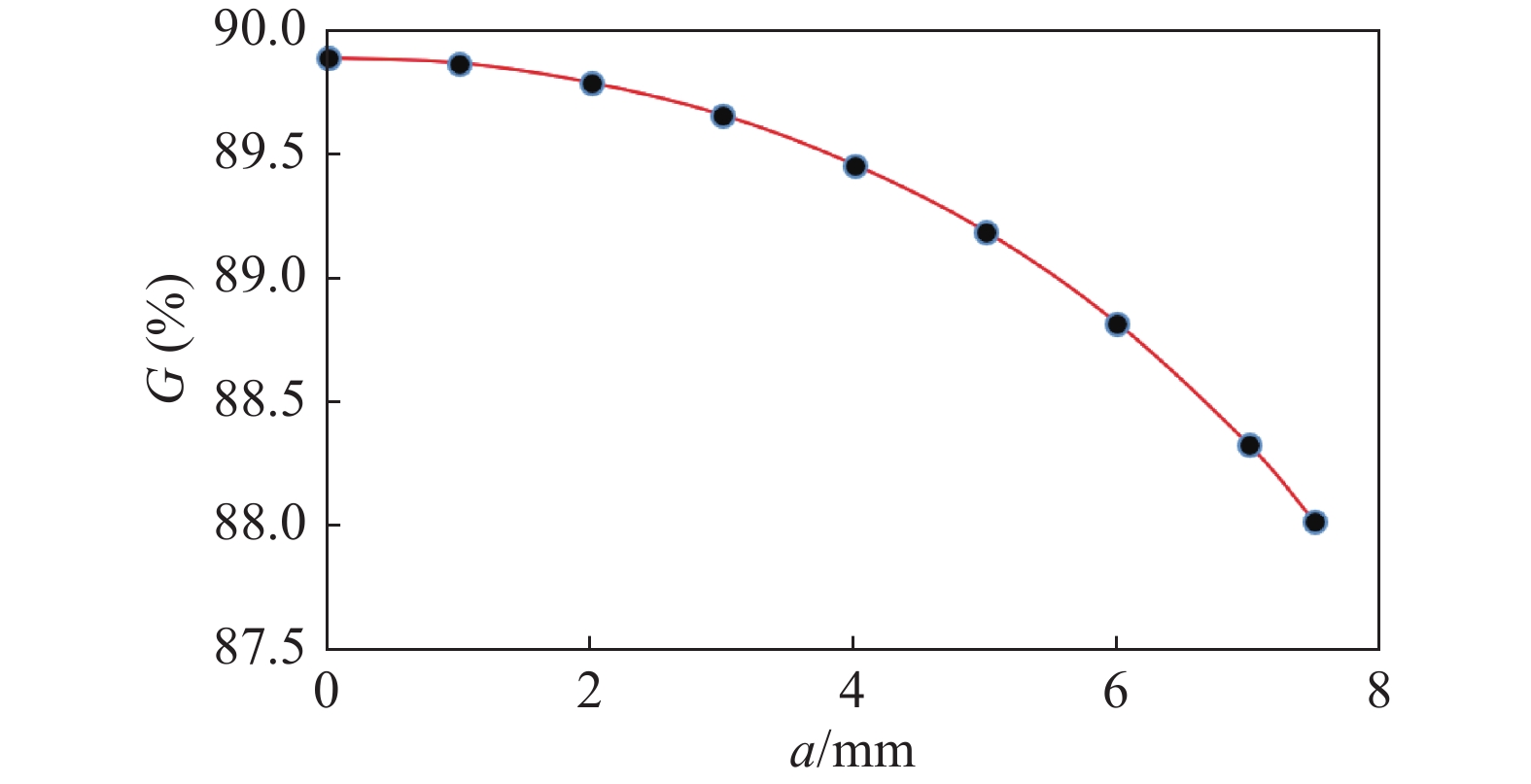
1.2 a值的变化对几何因子的影响如果R3 = 15 mm,R1 = 12.5 mm,h = 2 mm,R2 = R4 = 22.5 mm,a的变化范围为[0,7.5] mm,G值随a值的变化情况如表2和图4所示:保持其他参数不变,G值随着a值的增大而减小,减小的幅度越来越大,在a = 0 mm时,G值最大,也就是说平面源与探测器窗正对时发射到探测窗内的放射性粒子最多。
|
|
表 2 G值随a值的变化 Table 2 The change in G value with a value |
|
图 4 G值随a值的变化情况 Figure 4 The change in G value with a value |
Tsoulfanidis等[9]在著作中给出了本征探测效率的定义式:
| $ \mathrm{探}\mathrm{测}\mathrm{效}\mathrm{率} = \frac{\mathrm{单}\mathrm{位}\mathrm{时}\mathrm{间}\mathrm{内}\mathrm{探}\mathrm{测}\mathrm{器}\mathrm{记}\mathrm{录}\mathrm{到}\mathrm{的}\mathrm{净}\mathrm{粒}\mathrm{子}\mathrm{数}}{\mathrm{单}\mathrm{位}\mathrm{时}\mathrm{间}\mathrm{内}\mathrm{射}\mathrm{向}\mathrm{探}\mathrm{测}\mathrm{器}\mathrm{的}\mathrm{净}\mathrm{粒}\mathrm{子}\mathrm{数}} $ | (2) |
假设源是均匀的,自吸收、散射、探测器的死时间均不考虑,进入探测器窗的所有粒子都发生反应且收集处理效率是100% ,而且平面源与探测器窗在空间上是平行的,可以得到探测效率计算模型如下
| $ \varepsilon = \frac{N-{N}_{b}}{A\cdot G} $ | (3) |
上式中,G为几何因子,A为计量时标准平面源2π 球面度的表面发射率(min−1),N为测量到的总计数率(min−1),Nb为本底计数率(min−1)。
为研究a值对探测效率的的影响,需要考虑其引入的不确定度。从不确定的角度考虑,计数值越大,辐射探测中的统计涨落越小,引入的不确定度也越小,结果也就更可靠。
1.3.1 不确定度来源分析探测效率的不确定度的来源主要有以下4个方面:
1) 探测器计数统计涨落引入的不确定度。依据泊松分布[10],可以参照B类标准不确定度进行评定。
2) 本底涨落引入的不确定度。依据泊松分布,可以参照B类标准不确定度进行评定。
3) 标准平面源表面发射率A引入的不确定度。依据溯源证书,可以参照B类标准不确定度进行评定。
4) a值改变引起G值变化引入的不确定度。依据均匀分布,可以参照B类标准不确定度进行评定。
参考检定规程中的检定方法,进行如下探测效率的测量试验:将一个标准平面源放入待测仪器的样品盘中,源表面与探测窗平面的垂直距离为h,在仪器测量软件上设置测量次数为n1,每次测量t1min,每次测量计数为
| $ N = \frac{{n}_{2}}{{n}_{1}{t}_{1}} $ | (4) |
| $ {N}_{b} = \frac{{n}_{3}}{{t}_{2}} $ | (5) |
| $ {n}_{2} = {\sum }_{i}^{{n}_{i}}{N}_{i} $ | (6) |
各个分量之间独立不相关,各个分量的标准不确定度评定如下:
1) 依据泊松分布,第i次探测器计数的标准不确定度是
| $ u\left(N\right) = \frac{\sqrt{{n}_{2}}}{{n}_{1}{t}_{1}} $ | (7) |
2) 依据泊松分布,Nb的标准不确定度按照B类标准不确定度可以评定为
| $ u\left({N}_{b}\right) = \frac{\sqrt{{n}_{3}}}{{t}_{2}} $ | (8) |
(N−Nb)的相对标准不确定度可以表示为
| $ {u}_{rel}\left(N-{N}_{b}\right) = \frac{u(N-{N}_{b})}{N-{N}_{b}} $ | (9) |
3) 依据溯源证书,A的相对标准不确定度可以参照B类标准不确定度评定,溯源证书中的相对扩展不确定度是Urel,k = 2,那么相对标准不确定度是
| $ {u}_{rel}\left(A\right) = \frac{{U}_{rel}}{2} $ | (10) |
4) a ∈[0,R4−R3],几何因子G在[G(R4−R3),G(0)]范围内均匀分布,依照B类标准不确定度评定法,几何因子的相对标准不确定度为
| $ {u}_{rel}\left(G\right) = \frac{G\left(0\right)-G({R}_{4}-{R}_{3})}{2\sqrt{3}}\cdot \frac{1}{G\left(a\right)} $ | (11) |
各个分量的相对标准不确定度汇总表如表3。
|
|
表 3 各个分量的相对标准不确定度汇总表 Table 3 Relative standard uncertainty of each component |
根据不确定度传播率,我们可以得到探测效率的相对合成标准不确定度
| $ \begin{split} &{\left[\frac{{u}_{c}\left(\varepsilon \right)}{\varepsilon }\right]}^{2} = {\left[\frac{u\left(N-{N}_{b}\right)}{N-{N}_{b}}\right]}^{2} + {\left(\frac{{U}_{rel}}{2}\right)}^{2} +\\ &{\left[\frac{G\left(0\right)-G\left({R}_{4}-{R}_{3}\right)}{2\sqrt{3}}\cdot \frac{1}{G\left(a\right)}\right]}^{2} \end{split} $ | (12) |
观察到上述等式右侧第一项中N远大于Nb, 所以可以简写成
| $ {\left[\frac{u\left(N-{N}_{b}\right)}{N-{N}_{b}}\right]}^{2}\approx \frac{u\left(N\right)}{N} = \frac{1}{\sqrt{{n}_{2}}} $ | (13) |
显然
等式(12)中右侧第3项值与G(a)的平方成反比,G(a)值更大时,该项值更小,G(0)最大,该项值最小。因此a = 0时的探测效率的相对合成标准不确定度更小。
2 结 果为验证a值变化对探测效率及其不确定度的影响,使用经溯源的α、β平面源对探测器进行实验。
2.1 β平面源的实验 2.1.1 实验器材和参数选用2台仪器进行实验,分别是闪烁体型低本底α、β测量仪FYFS-400X(以下简称FYFS-400X)和流气正比计数器总α、总β测量仪MPC-9604(以下简称MPC-9604),选择在溯源证书中满足检定要求的一个测量通道进行实验。
该次实验所用的平面源和仪器的参数如下:
(1)标准平面源的信息:使用90Sr-90Y平面源,溯源证书上的2π球面度表面发射率是27700 min−1(参考日期2020.04.23),Urel = 2.5%,k = 2。平面源厚度1 mm,外径30 mm,活性区直径25 mm。
(2)FYFS-400X的信息
探测器窗与样品盘直径均是45 mm,探测器窗与源表面的垂直距离h = 2 mm。
(3)MPC-9604的参数信息
探测器窗直径是57 mm,样品盘直径是51 mm,h = 3 mm。
测量参数设置如下:
本底均测量24 h,然后放入标准平面源,分别将其置于a = 0 mm和a = (R4−R3) mm处,设置单次测量时间为2 min,测量次数为10次,其他测量条件保持一致。
2.1.2 实验结果不同a值处的2π球面度的几何因子G(a)和相对标准不确定度计算结果如表4。
|
|
表 4 两台仪器不同a值处的几何因子值及探测效率计算值 Table 4 Geometric factor values and detection efficiency values at different a values of the two instruments |
表4显示2类仪器的相对标准不确定度确实是几何因子G(a)最大的时候更小。
检定规程中给出的探测效率计算公式可表示为
| $ \varepsilon = \frac{N-{N}_{0}}{A} $ | (14) |
上式中:
可以看出,根据上式的计算方法,由于居中会让进入探测窗的粒子数更大,自然会使得a = 0时的探测效率更大,如表4所示,其中a最大时FYFS-400X探测效率偏小1.2%,MPC-9604探测效率偏小3.2%,仪器计量时如果不能确保标准平面源位于样品盘正中央,会使得探测效率偏小,可能会导致仪器的探测效率无法满足检定规程的要求,进而出不了有合格结论的检定证书。
2.2 α平面源的实验 2.2.1 实验器材和参数使用流气正比计数器总α、总β测量仪MPC-9604(以下简称MPC-9604),选择在溯源证书中满足检定要求的一个测量通道进行实验。
该次实验所用的平面源和仪器的参数如下:
(1)标准平面源的信息:使用241Am α平面源,溯源证书上的2π球面度表面发射率是15500 min−1(参考日期2020.02.26),Urel = 2.5%,k = 2。平面源厚度1 mm,外径30 mm,活性区直径25 mm。
(2)MPC-9604的参数信息
探测器窗直径是57 mm,样品盘直径是51 mm,h = 3 mm。
测量参数设置如下:
本底均测量24 h,然后放入标准平面源,分别将其置于a = 0 mm和a = (R4−R3) mm处,设置单次测量时间为2 min,测量次数为10次,其他测量条件保持一致。
2.2.2 实验结果不同a值处的2π球面度的几何因子G(a)和相对标准不确定度计算结果如表5。
|
|
表 5 仪器不同a值处的几何因子值及探测效率计算值 Table 5 Geometric factor values and detection efficiency values at different a values of MPC-9604 |
表5显示2类仪器的相对标准不确定度在几何因子G(a)最大时更小。也可以看出,根据检定规程中式(14)的计算方法,标准平面源居中会让进入探测窗的粒子数更多,自然会使得a = 0时的探测效率更大,其中a最大时MPC-9604探测效率偏小1.9%,因此仪器计量时如果不能确保标准平面源位于样品盘正中央,会使得探测效率偏小,进而会出现和β平面源实验一样的后果。
3 讨 论目前带铅室用于获得较低本底的α、β放射性测量仪应用广泛,尤其在环境样品的监测中,如樊芳等[11]利用FYFS-400X型α、β测量仪对昆明某基地蔬菜的总α、β放射性水平进行了测量分析,李林泽等[12]使用FYFS-400X型仪器研究了南京市 24 个地下水监测井中水样的总 α、总 β 放射性水平,赵坤等[13]使用BH1216Ⅲ型仪器研究了大亚湾、岭澳核电站周围生活饮用水中总 α、总 β 放射性水平,曾亚楠等[14]使用BH1227型仪器研究无锡市环境样品中总 α和总 β放射性水平,熊强等[15]利用LB4200型仪器研究了土壤中总 α、总 β放射性检测方法的比较,罗茂丹等[16]使用MPC9604型仪器研究了水中总 α、总 β 测量的实验室质量控制。作为实验室分析仪器,这些低本底α、β放射性测量仪需要进行周期溯源以保证其计量特性满足一定的要求。
使用圆面源对低本底α、β测量仪和流气正比计数器总α总β测量仪进行计量已然很普遍,放射源的传递量值是2π球面度的表面发射率,仪器终端的示值一般是计数率,计量过程中源与探测器几何位置的改变会导致立体角改变,进而使得几何因子发生变化,几何因子变化会直接影响进入到探测窗的粒子数目,一般情况下,平面源居中置于样品盘会有更多的放射性粒子进入到探测窗,这也进一步影响到仪器的探测效率,而且考虑到放射性计数的统计涨落,进入到探测窗的放射性粒子越多,探测系统的计数相应会变大,其相对涨落就会更小,引入的不确定度也会更小,这也使得最终的结果更加可靠。
本文着眼于仪器计量实际场景,重点从活性区半径和间距变化两个方面来讨论对探测效率的影响,在检定规程要求的范围内,活性区半径越小,几何因子越大,这有利于获得更好的探测指标;而不居中放置,会导致平面源与探测窗发生错位,几何因子相对也会变小,这不利于更好地评价仪器的探测性能。实验结果显示FYFS-400X或MPC9604,对于β平面源的探测受到间距a变化的影响;MPC9604对于α平面源的探测也受到相同的影响,相信其他类型的α、β放射性测量仪对于α、β平面源的探测也遵循这个结果。
本文研究说明一方面宜使标准平面源的活性区半径与实验室在样品盘上铺设的样品半径保持相同,以寻求立体角的一致;另一方面在将平面源置于样品盘中对仪器进行计量时,需要考虑活性区中心与探测窗中心位置间距的变化对几何因子的影响,间距越小,几何因子越大,宜将平面源居中放置。本文研究也得出将标准平面源置于样品盘正中央,不仅使几何因子的变化引入的相对标准不确定度更小,而且按照检定规程中的探测效率计算方法,居中相比其他位置能够有更大的探测效率。进一步也可以看出目前的检定规程在计算探测效率时没有考虑到几何因子或者直接假设几何因子G为1,这与实际情况不符。本文的实验结果计算表明依据检定规程计算的探测效率会比考虑了几何因子的探测效率偏小,对于FYFS-400X,测量β源时会偏小11.2%;对于MPC-9604,测量β源时会偏小12.8%,测量α源时会偏小12.8%。
总之,将平面源居中置于样品盘测量,既能获得更大的探测效率,也能获得更小的不确定度,所以无论是日常仪器质控还是周期检定,都应该采取有效措施确保平面源始终置于样品盘正中央。
| [1] |
Ruffle MP. The geometrical efficiency of a parallel-disc source and detector system[J]. Nucl Instrum Methods, 1967, 52(2): 354-356. DOI:10.1016/0029-554X(67)90248-0 |
| [2] |
Ruby L, Rechen JB. A simpler approach to the geometrical efficiency of a parallel-disk source and detector system[J]. Nucl Instrum Methods, 1968, 58(2): 345-346. DOI:10.1016/0029-554X(68)90491-6 |
| [3] |
Gardner RP, Verghese K. On the solid angle subtended by a circular disc[J]. Nucl Instrum Methods, 1971, 93(1): 163-167. DOI:10.1016/0029-554X(71)90155-8 |
| [4] |
倪光炯, 陶宗英. 圆盘面对放射性面源所张平均立体角的计算[J]. 核技术, 1979, 2(4): 14-20. Ni GJ, Tao ZY. Calculation of the average solid Angle of a disk facing a radioactive surface source[J]. Nucl Tech, 1979, 2(4): 14-20. |
| [5] |
Conway JT. Generalizations of Ruby's formula for the geometric efficiency of a parallel-disk source and detector system[J]. Nucl Instrum Methods Phys Res Sect A:Accel Spectrom Detect Assoc Equip, 2006, 562(1): 146-153. DOI:10.1016/j.nima.2006.02.197 |
| [6] |
刘宗良, 周剑良. 圆面探测器对圆面源几何因子的蒙特卡罗计算[J]. 科技资讯, 2008, 6(6): 251-252,254. Liu ZL, Zhou JL. Monte Carlo Calculation of geometrical factor of Circular surface source by Circular surface detector[J]. Sci Technol Inf, 2008, 6(6): 251-252,254. DOI:10.3969/j.issn.1672-3791.2008.06.210 |
| [7] |
国家质量监督检验检疫总局. JJG 853—2013 低本底α、β测量仪[S]. 北京: 中国标准出版社, 2014. General Administration of Quality Supervision, Inspection and Quarantine. JJG 853—2013 Low background alpha/beta measuring instruments[S]. Beijing: Standards Press of China, 2014. |
| [8] |
国家质量监督检验检疫总局. JJG 1100—2014 流气正比计数器总α、总β测量仪检定规程[S]. 北京: 中国质检出版社, 2014. General Administration of Quality Supervision, Inspection and Quarantine. JJG 1100—2014 Gas-flow proportional counter gross alpha and gross beta measuring instruments[S]. Beijing: China Quality Inspection Press, 2014. |
| [9] |
Tsoulfanidis N, Landsberger S. Measurement and detection of radiation[M]. 4th Ed. Boca Raton: CRC Press, 2015. DOI: 10.1201/b18203.
|
| [10] |
Knoll GF. Radiation detection and measurement[M]. 4th Ed. Hoboken: John Wiley & Sons, Inc. , 2010.
|
| [11] |
樊芳, 杨波, 秦启凤, 等. 昆明某基地蔬菜中总α和总β放射性水平调查与分析[J]. 中国辐射卫生, 2020, 29(5): 503-506. Fan F, Yang B, Qin QF, et al. Monitoring and analysis of gross α and gross β radioactivity levels in vegetables base in Kunming[J]. Chin J Radiol Health, 2020, 29(5): 503-506. DOI:10.13491/j.issn.1004-714X.2020.05.015 |
| [12] |
李林泽, 朱锐, 刘飞, 等. 南京市地下水总α、总β放射性水平研究[J]. 中国辐射卫生, 2020, 29(5): 507-509,514. Li LZ, Zhu R, Liu F, et al. Determination of gross-α and gross-β activities in groundwater of Nanjing City[J]. Chin J Radiol Health, 2020, 29(5): 507-509,514. DOI:10.13491/j.issn.1004-714X.2020.05.016 |
| [13] |
赵坤, 林涌钦, 蔡金敏, 等. 核电站周围饮用水中总α、总β放射性水平研究[J]. 中国辐射卫生, 2019, 28(6): 681-683. Zhao K, Lin YQ, Cai JM, et al. A reaserch on total alpha and total beta radioactivity in drinking water around[J]. Chin J Radiol Health, 2019, 28(6): 681-683. DOI:10.13491/j.issn.1004-714X.2019.06.022 |
| [14] |
曾亚楠, 朱晓明, 姚誉阳, 等. 2014—2019年无锡市环境样品总α和总β放射水平调查[J]. 中国辐射卫生, 2022, 31(1): 17-22. Zeng YN, Zhu XM, Yao YY, et al. Gross α and gross β radioactivity of environmental samples in Wuxi, China, 2014-2019[J]. Chin J Radiol Health, 2022, 31(1): 17-22. DOI:10.13491/j.issn.1004-714X.2022.01.004 |
| [15] |
熊强, 葛潇, 闫琳琳, 等. 土壤中总α、总β放射性检测方法的比较[J]. 中国辐射卫生, 2023, 32(3): 245-249. Xiong Q, Ge X, Yan LL, et al. Comparison of methods for determination of gross α and gross β radioactivity in soil[J]. Chin J Radiol Health, 2023, 32(3): 245-249. DOI:10.13491/j.issn.1004-714X.2023.03.005 |
| [16] |
罗茂丹, 李斌, 李雪泓, 等. 水中总α、总β测量的实验室质量控制[J]. 四川环境, 2017, 36(2): 57-61. Luo MD, Li B, Li XH, et al. Laboratory quality control of gross alpha and gross beta radioactivity measurement in water[J]. Sichuan Environ, 2017, 36(2): 57-61. DOI:10.3969/j.issn.1001-3644.2017.02.012 |



