2. 苏州大学医学部放射医学与防护学院,江苏 苏州 215123;
3. 中国计量科学研究院,北京 100029
2. School of Radiation Medicine and Protection, Medical College of Soochow University, Suzhou 215123 China;
3. National Institute of Metrology, Beijing 100029 China
随着各国对核电需求的增加及核能的广泛应用,我国作为拥有最大规模在建核电站的国家,日益重视起对放射性惰性气体流出物的监测以及对核辐射突发事件开展应急卫生工作[1-2]。核电站反应堆工作与核爆试验过程中都会产生放射性惰性气体,如133Xe、135Xe、37Ar、85Kr等,其中133Xe、37Ar已被全面禁止核试验条约组织确定为现场视察(on-site inspections,OSI) 的核查核素 (CTBT/PC-10/1/Annex II,Appendix VIII)[3]。对放射性惰性气体活度浓度的准确测量是提升核技术发展能力与监测各国核辐射突发事件信息、采取应急反应举措与快速组织有效核防护的关键。
分析环境中放射性活度较低的样品时,探测效率对准确获得放射性核素活度至关重要[4]。37Ar通过核爆过程或核反应堆中40Ca(n,α)Ar37反应产生,半衰期为35.04 d,衰变方式为轨道电子俘获。其中,K壳层发射的俄歇电子能量为2.82 keV, 占分支比81.5%;特征X射线能量为2.82 keV,分支比为8.7%;L壳层发射的俄歇电子或X射线能量为0.27 keV,分支比为8.9%[5]。37Ar作为惰性气体,衰变射线能量低,内充气正比计数器法是具有高探测效率的37Ar活度测量方法。但基于内充气正比计数器,必需考虑测量装置电子学系统死时间、本底、端效应、阈值以下漏计数等因素对测量结果的影响,对测量计数率进行相应的修正[6]。
在对放射性惰性气体计数率进行修正过程中,死时间和本底修正可通过优化测量系统、增加屏蔽体实现;端效应则可通过长度补偿法予以修正[5]。但阈值以下漏计数的损失无法直接测量,实验上一般采用改变电子学下阈值和改变气压的方式进行外推修正[7],或在压强难以改变时,运用蒙特卡罗模拟确定修正因子。本文通过蒙特卡罗理论计算的方法,构建正比计数器模型并获得37Ar能量沉积谱,模拟不同条件下探测效率及计数损失差异,研究得到计数损失修正因子,为提高实验中37Ar活度测量的效率与准确性提供理论支撑。
1 材料与方法 1.1 Geant4软件本文基于Geant4蒙特卡罗模拟软件[8],对37Ar活度绝对测量过程中漏计数修正方法与修正因子等开展系统研究。Geant4是一个基于C + + 编写的开源软件包,用于准确地模拟粒子在物质中的运输及参与的物理过程,主要包括几何体与材料构造、粒子径迹及物理过程、探测器灵敏度、轨迹存储与可视化、结果读取与分析等[8]。Geant4提供一系列物理模型来描述射线和物质相互作用过程,用户可以依需自由选择。依据37Ar的衰变特性及粒子能量范围,本模拟使用Geant4内建的物理过程包FTFP_BERT。该物理过程包可以较好描述输入能量仅为几个keV的粒子所发生的光电效应等物理过程。程序的模拟结果以ROOT文件格式存储,并基于ROOT进行数据分析[9]。
1.2 正比计数器建模正比计数器是一种气体探测器,因其高增益和低噪音,适用于探测低能X/β射线。尤其,在进行活度测量时,对β射线的探测效率接近百分之百[10]。本研究工作中,为了便于将模拟结果与实验数据对比,在探测器建模方面,选取已进行过测量实验的移动式37Ar快速探测系统 (movable 37Ar rapid detection system, MARDS)[11]所采用的LND 4953型正比计数管。该计数管总长550 mm, 灵敏体积为950 ml, 内置工作气体为P10(氩甲烷混合气体),实验常用压强60 kPa。构造示意图如图1,模型输入参数见表1[12]。
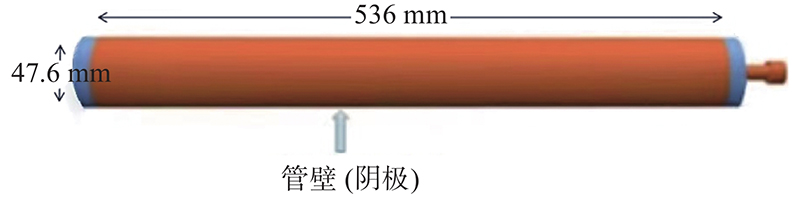
|
图 1 正比计数器结构 Figure 1 Schematic of proportional counter |
|
|
表 1 蒙卡输入模型参数 Table 1 Parameters used in the Monte Carlo model |
本程序将发生1次电子俘获衰变定义为发生1个Event(事件),多次Event组成运行执行程序Run。将工作气体区设置为灵敏体积,气体压强可调。粒子发射位置均匀分布在圆柱体内,以衰变道形式将2.82 keV电子与2.82 keV光子按照各自分支比抽样。发射方向为4π同性,输出粒子径迹与能量沉积结果。为了增加运行结果的普遍性与减小误差,每种条件均模拟了106个事件。参考实际应用的内充气正比计数器的能量分辨率和信噪比,对输出数据进行能量分辨率为20%的高斯展宽,对应X射线和俄歇电子的能峰位置,选择1.5 keV为下阈值,3.5 keV为能峰上阈值。结果输出模型可视化视图、能量沉积谱、探测粒子计数(除以输入粒子数106即为探测效率)。
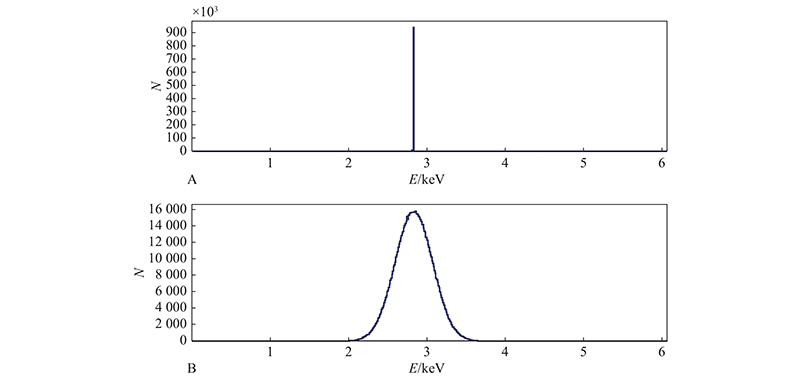
2 结 果 2.1 37Ar探测效率与计数损失将37Ar衰变过程中释放的俄歇电子和特征X射线按照各自分支比与能量对应输入后,在60 kPa下获得粒子运行轨迹及粒子能量沉积谱如下图2、3,其中横轴为粒子在计数管中沉积的能量E,纵轴为计数N。

|
图 2 粒子轨迹可视化视图 Figure 2 Particle trajectory visualization |
|
图 3 37Ar能量沉积谱 Figure 3 Energy deposition spectrum of 37Ar 注:A.原始图谱;B.高斯展宽图谱。 |
可以看出,由于37Ar衰变产生单能粒子,与工作气体相互作用几乎将能量全部沉积在灵敏体积内,并在2.8 keV左右形成单能峰。因此活度测量时无需进行阈值以下的小脉冲幅度修正,实验上对小脉冲计数损失的处理,只需以峰计数除以能量衰变分支比0.902即可得到修正后计数。
当37Ar衰变产生的粒子与工作气体发生相互作用时,将能量损失在气体介质中,产生电子-离子对被正比计数管内电极收集[13]。理论上,对于2.82 keV的低能粒子而言,发生电离相互作用后产生的离子对可将能量全部沉积在灵敏体积内,正比计数器对电子探测效率应趋近100%。但由图3模拟结果表明,在输入初始粒子数106的前提下,正比计数管灵敏体积对粒子探测效率为93.5%。对于模拟探测效率与理论数值的差异,考虑是由于37Ar衰变同时发射俄歇电子和X射线2种不同粒子所导致。因此分别将电子和X射线按分支比单独进行模拟以分析差异来源。经模拟发现当输入低能俄歇电子时正比计数管灵敏体积探测效率高达99.9%,说明能量几乎完全沉积;输入光子灵敏体积探测效率仅为38.7%,说明在设置的0.6个大气压的情况下,仅有少部分光子在工作气体内沉积能量。在能量小于10 keV时,X射线与物质主要发生光电效应被吸收,其中K壳层发生几率最大,约占80%,每个原子所发生光电效应的总截面σ可近似表示为[14]:
| $ \sigma =\frac{K{Z}^{5}}{{E}_{\gamma }^{n}} $ | (1) |
式中,Z为吸收物质的原子序数;Eγ为γ光子能量;n为常数,从低能的7/2到高能的1;K为常数。可以看出,光电反应截面与原子序数有强烈的依赖关系,P10气体组分为低原子序数物质氩甲烷,光子与工作气体反应截面积较小,靠近计数器管壁区域的粒子直接逃逸出灵敏区域,沉积在阴极壁上而不被探测到产生漏计数,因此37Ar活度测量过程中计数损失主要来源于光子逃逸产生的“壁效应”。
2.2 37Ar活度测量壁效应修正对于发生在探测器壁附近的衰变事件,当粒子向管壁方向发射时,有较大的概率不被测量。随着灵敏体积内工作气体压力增加,气体对探测射线的阻止能力增强,带电粒子沉积能量增加[15]。因此由计数器有限边界区域引起的“壁效应”漏计数损失,会随着计数器灵敏体积内工作气体压强增加而减小。根据正比计数器对电子和光子探测效率模拟结果的差异,分别对2种粒子进行模拟,分析俄歇电子及X射线壁效应随压强的变化情况。取60、90、120、150、180、210、240、270、300 kPa 9个点,得到不同压强倒数下探测效率结果如图4所示。

|
图 4 不同压强下37Ar探测效率曲线图 Figure 4 37Ar detection efficiency at different pressures |
可以看出随着压强改变,电子探测效率变化不大,对X射线影响较大,压强低时X射线探测效率低,在100 kPa以下低于50%,随着压强增加壁效应显著减小,且呈高阶项曲线变化趋势。依据上述模拟结果,对壁效应产生计数损失的修正应通过改变气体压强,获取不同压强下的计数,并按照适合的函数形式进行曲线拟合后外推至无穷大压强时的探测粒子数。为研究最优修正方法,增加低压条件30 kPa, 模拟由低至高不同工作气体压力下灵敏体积内粒子能量沉积计数,采取对压强倒数与模拟探测计数多项式拟合(式2),以及压强与模拟探测计数指数拟合(式3)两种常用修正方式,其中x为计数管工作气体压强,kPa;y为压强为x时,计数管探测的样品计数。图5为模拟拟合曲线。

|
图 5 不同压强下37Ar衰变的能量沉积计数 Figure 5 Energy deposition counts of 37Ar decay at different pressures 注:A.30~300 kPa;B.30~300 kPa;C.90~300 kPa;D.90~300 kPa。 |
| $ y = {k_1}x + {k_2}{x^2} + b $ | (2) |
式中,k1, k2, b为待定常数。
| $ y = {{\mathop A\nolimits_2 + (\mathop A\nolimits_1 - \mathop A\nolimits_2 )} \mathord{\left/ {\vphantom {{\mathop A\nolimits_2 + (\mathop A\nolimits_1 - \mathop A\nolimits_2 )} {\left( {1 + {{\left( {{x \mathord{\left/ {\vphantom {x {{x_0}}}} \right. } {{x_0}}}} \right)}^p}} \right)}}} \right. } {\left( {1 + {{\left( {{x \mathord{\left/ {\vphantom {x {{x_0}}}} \right. } {{x_0}}}} \right)}^p}} \right)}} $ | (3) |
式中,A1, A2, x0, p均为待定常数。
由模拟结果图5A、图5B可见,当工作气体压强低于90 kPa时,壁效应随压强变化幅度较大;高于90 kPa时,壁效应随压强变化幅度减小,故选取90~300 kPa压强进行探测计数模拟,结果如图5C、图5D所示。对30~300 kPa的计数采用多项式拟合压强倒数外推方法偏差为0.88%,压强与探测粒子计数指数拟合方法偏差为0.61%;对90~300 kPa进行多项式拟合压强倒数外推方法偏差为0.10%,压强与探测粒子计数指数拟合方法偏差为0.29%。因此为获得更精确的37Ar活度浓度测量结果,实验上可将工作气体压强设置为100 kPa以上,以此降低压强外推得到的壁效应漏计数修正因子的不确定度。然而,考虑到实际实验条件下,稳定的高气压条件往往不易实现,且高气压条件下,经调节后的正比计数器的工作电压也会随之增高。为此,选取与中国工程物理研究院进行37Ar活度测量实验所设置对应的100、150、200、250、300、350、400 kPa 7组压强[11],采用不同压强倒数与探测计数进行多项式拟合并外推至零,即获得压强无穷大时的计数,除以各压强下的探测计数得到修正因子,结果列于表2。通过数据拟合及模拟修正因子分析可得,100 kPa下37Ar活度测量壁效应影响为4.4%,随着压强增大,修正因子逐渐减小,总体而言,每个压强点下得到的修正因子模拟结果与实验结果的相对偏差在0.6%以内。
|
|
表 2 不同压强下37Ar壁效应计数损失修正因子 Table 2 Correction factor of 37Ar counting loss due to wall effect at different pressures |
本文基于Geant4模拟放射性惰性气体37Ar活度浓度测量过程中计数损失产生原因及修正方法,发现37Ar衰变释放X射线对探测效率影响较大,漏计数损失主要来自光子产生的壁效应。但因X射线所占分支比小于10%,其余为将能量全部沉积在灵敏体积内的电子,计数管对37Ar总探测效率仍然可达到90%以上,因此可以采用正比计数器法实现37Ar活度绝对测量。
当气体压强无穷大时,没有射线逃逸出计数器的灵敏体积,壁效应引起的漏计数趋于零[15]。对壁效应引起的漏计数损失修正通过增加工作气体压强,采用不同压强倒数与计数进行多项式拟合,并获取修正因子的方法实现。使用Geant4构建正比计数管模型,模拟探测计数并获取不同压强下修正因子,结合实验压强下测量得到的计数率即可获得放射性核素活度测量结果,可避免实验中调节压强所引起工作电压、上下阈值的改变而对测量结果产生影响。后续可基于此Geant4程序模拟不同衰变特性放射性惰性气体如85Kr、3H等,对阈值以下计数损失进行分析和修正,并优化实验操作条件,实现放射性惰性气体活度浓度准确测量。
| [1] |
陈惠芳, 袁龙, 付熙明, 等. 国家核辐射突发事件卫生应急队伍组建与管理探讨[J]. 中国辐射卫生, 2021, 30(2): 201-204. Chen HF, Yuan L, Fu XM, et al. Discussion on establishment and management of national health emergency team for nuclear radiation emergency[J]. Chin J Radiol Health, 2021, 30(2): 201-204. DOI:10.13491/j.issn.1004-714X.2021.02.017 |
| [2] |
王自路, 王伟, 拓飞, 等. 我国放射性惰性气体Kr、Xe监测体系的溯源现状[J]. 中国辐射卫生, 2019, 28(6): 730-733. Wang ZL, Wang W, Tuo F, et al. Current status of traceability of radioactive inert gas (Kr、Xe) monitoring system in China[J]. Chin J Radiol Health, 2019, 28(6): 730-733. DOI:10.13491/j.issn.1004-714X.2019.06.035 |
| [3] |
Kirchner G, Gerfen F, Heise A, et al. Will 37Ar emissions from light water power reactors become an obstacle to its use for nuclear explosion monitoring?[J] J Environ Radioact, 2020, 223-224: 106392. DOI: 10.1016/j.jenvrad.2020.106392.
|
| [4] |
王硕, 杨宝路, 周强, 等. 无源效率刻度在马林杯状气体源活度测量中的应用[J]. 中国辐射卫生, 2022, 31(1): 6-12. Wang S, Yang BL, Zhou Q, et al. Application of sourceless efficiency calibration in activity measurement of gas source in Marinelli beaker[J]. Chin J Radiol Health, 2022, 31(1): 6-12. DOI:10.13491/j.issn.1004-714X.2022.01.002 |
| [5] |
Cleveland BT, Daily T, Davis R Jr, et al. Measurement of the solar electron neutrino flux with the homestake chlorine detector[J]. Astrophys J, 1998, 496(1): 505. DOI:10.1086/305343 |
| [6] |
李奇, 樊元庆, 王世联, 等. 低本底内充气正比计数管测量37Ar活度
[J]. 原子能科学技术, 2019, 53(4): 734-738. Li Q, Fan YQ, Wang SL, et al. Measurement of 37Ar activity by low background internal gas proportional counter [J]. At Energy Sci Technol, 2019, 53(4): 734-738. DOI:10.7538/yzk.2018.youxian.0453 |
| [7] |
Mori C, Wu Y, Agemura T, et al. Evaluation of counting loss and its correction for small pulses in internal counting with proportional counters[J]. Appl Radiat Isot, 1998, 49(9/11): 1107-1111. DOI:10.1016/S0969-8043(97)10028-8 |
| [8] |
CERN Geant4 User’s Guide[EB/OL]. [2022-09-09]. http://geant4.web.cern.ch/geant4.
|
| [9] |
Brun R, Rademakers F. ROOT-An object oriented data analysis framework[J]. Nucl Instr Methods Phys Res Sect A:Accel, Spectr Detect Associat Equip, 1997, 389(1/2): 81-86. DOI:10.1016/S0168-9002(97)00048-X |
| [10] |
王自路, 李语奇, 张明, 等. 基于内充气正比计数器长度补偿法测量85Kr放射性活度浓度
[J]. 原子能科学技术, 2019, 53(12): 2465-2470. Wang ZL, Li YQ, Zhang M, et al. Radioactivity concentration measurement of 85Kr using length-compensated internal gas proportional counting method [J]. At Energy Sci Technol, 2019, 53(12): 2465-2470. DOI:10.7538/yzk.2019.youxian.0259 |
| [11] |
曹琳. 内充气正比计数管测量37Ar活度的探测效率研究[D]. 绵阳: 中国工程物理研究院, 2008. Cao L. Detection efficiency of 37Ar activity[D]. Mianyang: China Academy of Engineering Physics, 2008. |
| [12] |
LND, INC. Nuclear Radiation Detectors[EB/OL]. https://www.lndinc.com/products/special-products/4953.
|
| [13] |
复旦大学, 清华大学, 北京大学. 原子核物理实验方法[M]. 北京: 原子能出版社, 1981: 52-60. Fudan University, Tsinghua University, Peking University. Nucl phys exp methods[M]. Beijing: Atomic Energy Press, 1981: 52-60. |
| [14] |
于孝忠. 核辐射物理学[M]. 北京: 原子能出版社, 1981: 103-109. Yu XZ. Nuclear radiation physics[M]. Beijing: Atomic Energy Press, 1981: 103-109. |
| [15] |
王自路. 放射性惰性气体85Kr活度量值传递技术方法研究[D]. 北京: 中国疾病预防控制中心, 2020. DOI: 10.27511/d.cnki.gzyyy.2020.000088. Wang ZL. Research on technical methods of 85Kr activity standard transfer[D]. Beijing: Chinese Center for Disease Control and Protection, 2020. DOI: 10.27511/d.cnki.gzyyy.2020.000088. |




