2. 同方威视技术股份有限公司,北京 100084
2. Nuctech Company Limited, Beijing 100084 China
环境辐射样品的活度测量一般多用半导体探测器,这需要对探测器进行效率刻度[1-3]。为快速获得刻度结果,通常采用无源效率刻度方法,目前主要有蒙卡模拟方法和数值解析方法2类。蒙卡模拟方法通过对样品、探测器等进行精确建模并足量模拟射线在探测器中的输运过程及能量沉积而得到精确的探测效率,有很多通用或专用的蒙卡模拟程序如MCNP、GEANT4、FLUKA、DETEFF[4-5]等可供使用,但都存在计算时间较长的缺点;数值解析方法通过解析计算得到探测器对各类样品的探测效率,目前主要有虚拟点法、代表点法、效率转化法等方法[6-11],这类方法较蒙卡模拟方法的计算时间大大减少,但需要首先给出点源探测效率。作者所在研究室曾基于MCNP5开展过蒙卡与解析耦合的无源效率刻度方法研究[1],但只给出了点源及与探测器同轴的圆柱源的效率刻度方法。
为了对上述方法进一步扩展及优化,本文首先使用清华大学基于GEANT4工具包研发的蒙卡辐射防护设计与剂量计算软件THUDose[12]对多种类型探测器进行参数化建模,以方便获得点对点的探测效率网格;其次对探测效率网格插值后使用数值积分方法对7种常见样品进行解析,获得自吸收修正因子及探测效率;最终将蒙卡与解析方法的优点有效结合,实现一种可应用于多种探测器在常见类型样品活度测量场景下的无源效率刻度方法。
1 材料与方法对于点源,使用蒙卡模拟得到点对点探测效率网格,对于其它形状体源样品,方法则是将其分割为多个体积微元,每个体积微元可视为点源处理,把整体探测效率计算转化为空间任意位置点源探测效率的积分计算。
1.1 点源探测效率计算如图1,将探测器上表面

|
图 1 探测器测量点源示意图 Figure 1 Schematic diagram of point source measurement with a detector |
| $ eff(S) = \sum {eff({S_i})\frac{{dS}}{S}} $ | (1) |
其中,Si为探测器上表面某一面积为
若使用探测器上表面任意一点对空间中任意一处点源的探测效率作为探测效率网格,会消耗较多计算资源,基于下述2点性质,对点对点探测效率网格的蒙卡模拟进行简化。
1)在如图2探测器上表面任意一点A在真空情况下,对能量相同的点源S1、S2沿直线A-S1-S2发射的γ射线探测效率相同;
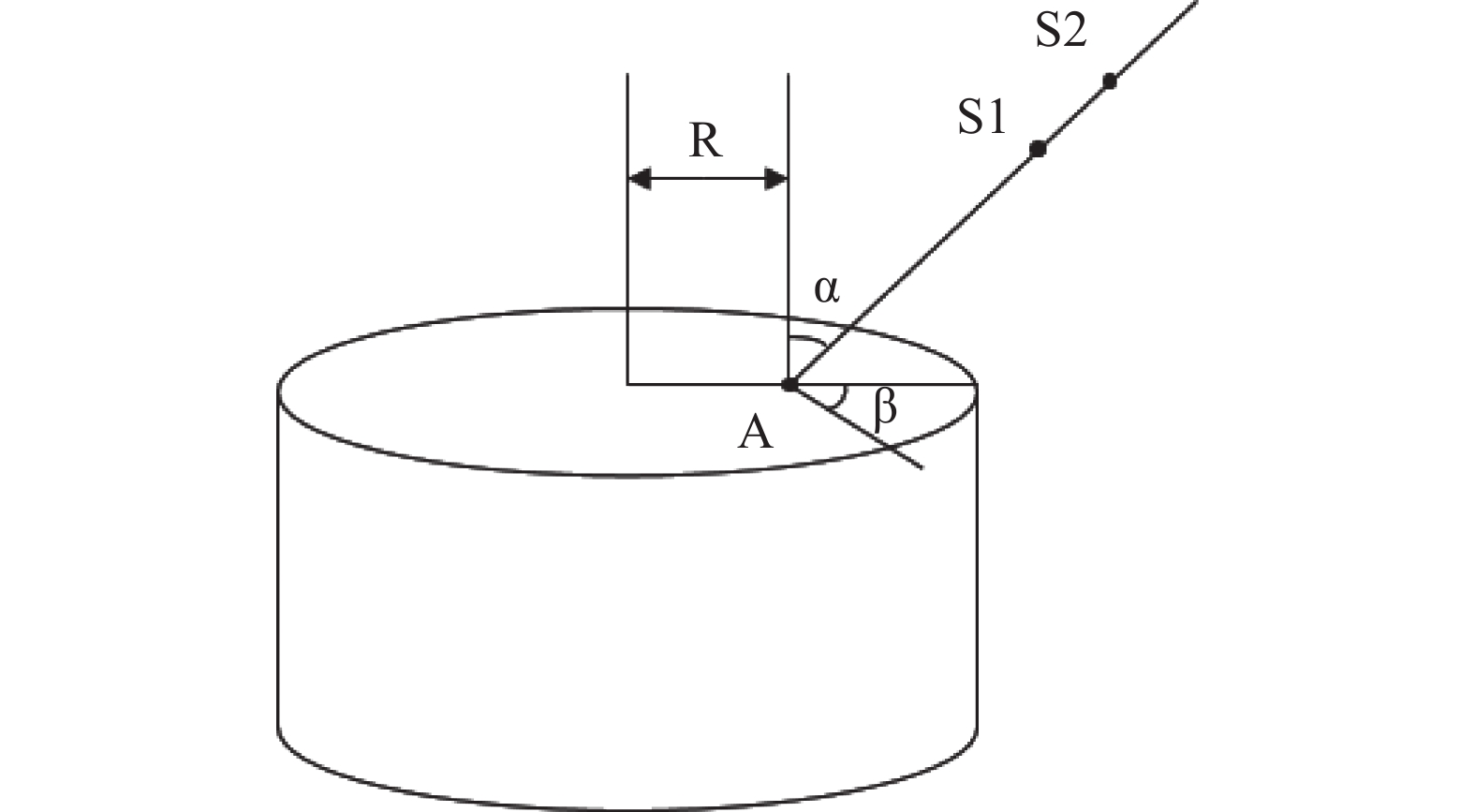
|
图 2 探测效率网格简化示意图 Figure 2 Schematic diagram of detection efficiency grid |
2)圆柱属于轴对称图形,探测器探头通常为圆柱形,选择探测器上表面任一条半径,其他所有半径均可通过旋转与该半径重合。
简化方案如下:选择探测器上表面一条半径,在半径上划分若干个点,每个点代表一个面积微元,求各点对以之为球心的上半球面的所有角度(每个角度代表一个点源或体积微元)的探测效率,以此作为探测效率网格。
网格中使用的物理量已在图2中标记,R为A点距探测器上表面中心的距离,
本文对使用的HPGe探测器模型共划分了15个能量点、6个半径上的点、19个
计算点源探测效率计算完成后,对该效率进行数值积分,获得体源探测效率。探测器探头通常为轴对称的圆柱,通过2个值定义体积微元的坐标:1)体积微元到探测器上表面中心点的距离d;2)体积微元与探测器上表面中心点连线与探测器中轴线的夹角θ,如图3。
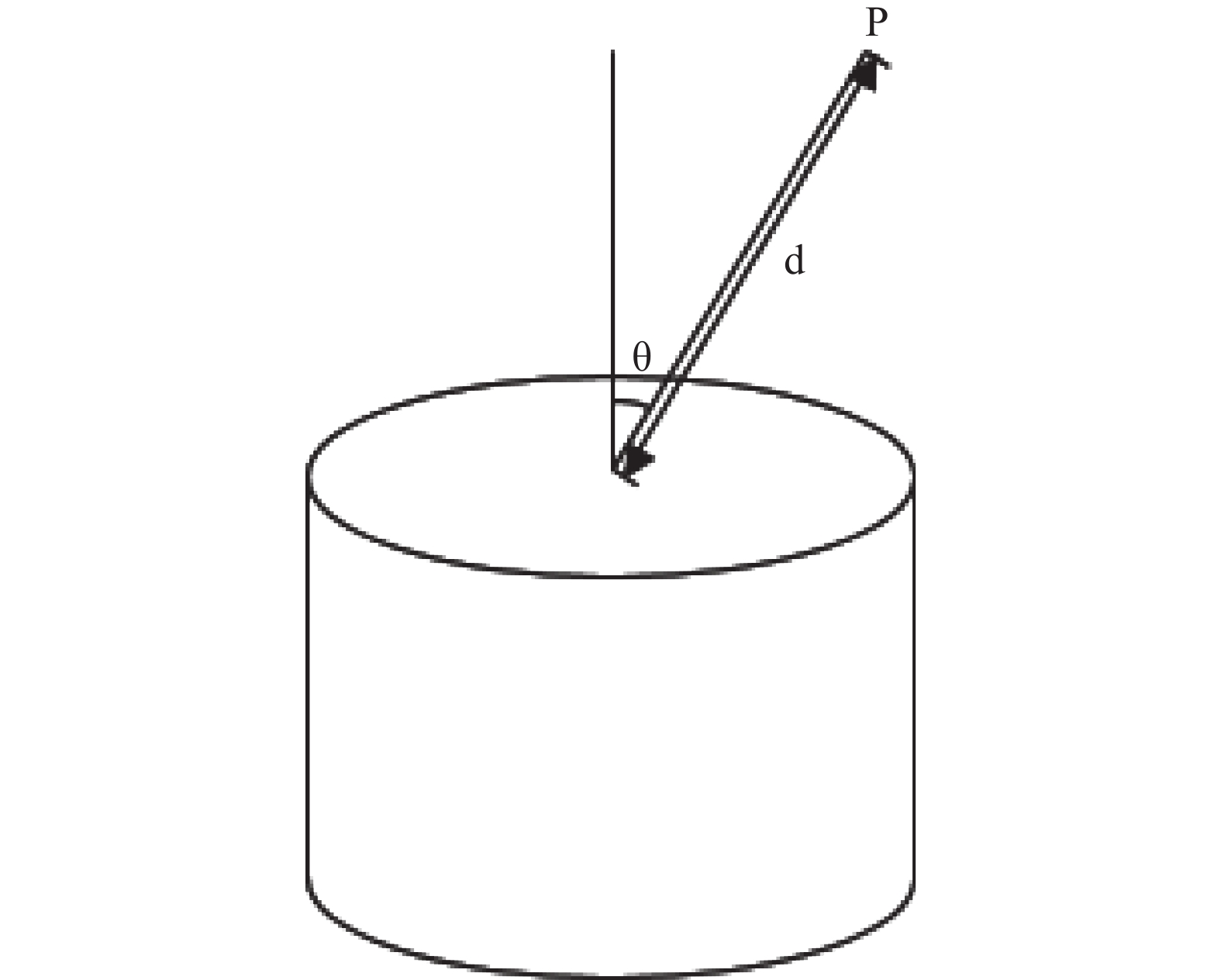
|
图 3 体积微元位置示意图 Figure 3 Schematic diagram of volume element position |
d与θ组成的体积微元坐标只能给出其与探测器上表面中心点的相对位置,探测效率网格存储的数据为点源与探测器上表面任意一点的相对位置,需要进一步转换坐标。对探测器上表面任意一点A,坐标为

|
图 4 探测器上表面示意图 Figure 4 Schematic diagram of detector upper surface |
基于d、θ、
| $ {{ef}}{{{f}}_P} = 2\int\limits_0^{{R_{\max }}} {\int\limits_0^\pi {eff({R_i},\alpha ,\beta ,{\rm E})\frac{{{R_i}d{R_i}d\delta }}{{4\pi {l^2}}}} } $ | (2) |
其中,系数2对应
体源内部的体积微元发射的γ射线经过体源样品材料的衰减才会被探测器探测到,在体源探测效率的计算公式中需引入体积微元的自吸收系数
| $ eff = 2\int\limits_0^V {\int\limits_0^{R\max } {\int\limits_0^\pi {eff({R_i},\alpha ,\beta ,E){f_{att}}\frac{{{R_i}d{R_i}d\delta }}{{4\pi {l^2}}}} } } \frac{{dV}}{V} $ | (3) |
其中,
| $ {f_{att}} = {e^{ - \mu t}} $ | (4) |
其中,
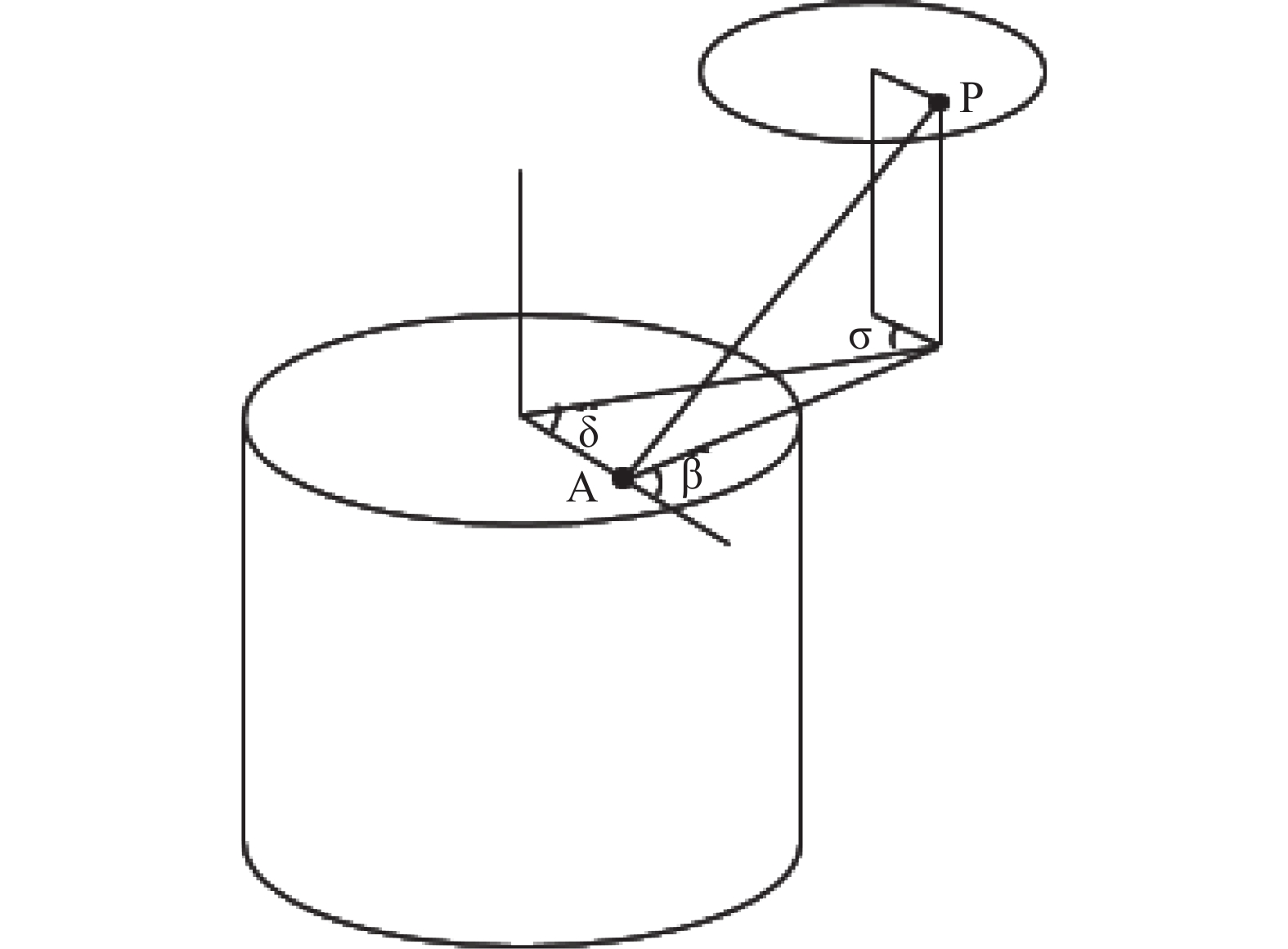
|
图 5 体积微元角度坐标信息 Figure 5 Angular coordinates of volume element |
| $ \alpha ' = \alpha \quad \beta ' = \sigma + (\beta - \delta ) $ | (5) |
其中,
以U型管样品为例,介绍样品自吸收系数的计算方法。
将U型管样品分为上下2部分,上部为圆柱,下部为球冠。以球冠的底面中心为参考点确定U型管样品与探测器的位置关系。如图6,设U型管样品整体高度为H0,圆柱半径为R0,球冠高为h,半径为r,设任意一体积微元的坐标为
|
图 6 U型管样品分割示意图 Figure 6 Schematic diagram of U-tube sample division |
分2类情况计算衰减距离。一类为
| $ t = \sqrt {{r^2} - R{'^2}} - r + H' $ | (6) |
另一类为
1)体积微元发出的γ射线从圆柱侧面出射时,衰减距离为:
| $ {{t}} = \frac{{R'\cos (\beta ') + \sqrt {{R_0^2} - {{(R'\sin (\beta '))}^2}} }}{{\sin (\alpha ')}} $ | (7) |
2)体积微元发出的γ射线从球缺出射时,衰减距离满足下列关系:
| $\begin{split}& {(t\sin (\alpha '))^2} + R{'^2} - 2t\sin (\alpha ')R'\cos (\beta ') =\\& {r^2} - {(r - H' + t\cos (\alpha '))^2} \end{split}$ | (8) |
实际情况下,放射源样品通过容器盛放,还需计算γ射线在容器材料中的衰减距离。重复前述步骤计算得到γ射线在考虑容器壁的U型管样品中的衰减距离
由式3)可得圆柱样品的总探测效率如下:
| $ \begin{split}& eff = 4\int\limits_0^\pi {\int\limits_0^{{R_{\max }}} {\int\limits_0^\pi {\int\limits_0^{{{\text{H}}_0}} {\int\limits_0^{{R_0}} {eff({R_i},\alpha ,\beta ,E){e^{ - {\mu _1}t}}{e^{ - {\mu _2}t'}}} } } } } \frac{{{R_i}d{R_i}d\delta }}{{4\pi {l^2}}}\frac{{dV}}{V} \\& d{V_{{\text{cy}}linder}} = \pi ({r^2_{i + 1}} - {r^2_i})dH\frac{{d\omega }}{{2\pi }} \\& d{V_{sphere}} = \frac{1}{3}\pi ({H_2^2}(3r - {H_2}) - {H_1^2}(3r - {H_1}))({k_{i + 1}^2} - {k_i^2})\frac{{d\omega }}{{2\pi }} \\& V = \frac{1}{3}\pi {h^2}(3r - h) + \pi {R_0^2}({H_0} - h) \\& dH = {H_2} - {H_1} \\[-15pt] \end{split} $ | (9) |
其中,μ1与μ2为γ射线在样品材料和容器材料中的线衰减系数,ri+1与ri为对圆柱半径R0等分后的半径,ki+1与ki为
本文采用上述耦合方法,实现了点源、圆盘、圆柱、烧杯、球形、U型管、马林杯7类代表性的样品的无源效率刻度计算模块构建,并对其计算正确性及计算时间进行了比较,此外采用该方法对一台HPGe探测器进行点源无源效率刻度并与有源刻度结果比对作为验证。
2.1 点对点效率网格计算对于不同型号的探测器,首先使用THUDose软件生成其相应的探测效率网格。THUDose软件中内置包括HPGe、LaBr3、NaI、CZT探测器等多种常用半导体探测器的结构模型,用户只需自定义探测器的参数即可完成探测器建模,特殊探测器模型可通过GDML文件自定义并导入。探测器建模完成后即可由THUDose内置蒙卡无源效率刻度模块快速获得探测器的探测效率网格。
2.2 体源耦合计算以圆柱样品为例,图7给出了基于耦合方法的无源效率刻度计算模块的实现流程。首先编制圆柱体源参数输入模块生成输入文件,提供探测器的型号,所测样品的模型编号,样品各部分详细参数和材料,吸收层参数和材料,以及需要测量的能量点等参数信息。输入文件提供的探测器型号将用于读取在第一步中生成的探测效率网格;将圆柱样品分割为m1×m2×m3个体积微元,计算体积微元相对探测器的位置和角度,采用插值法从探测效率网格得到体积微元在探测器每个面积微元对应的探测效率;下一步计算体积微元在圆柱样品中的位置和角度,计算衰减距离,获得自吸收系数;使用自吸收系数对探测效率修正,最终累加得到圆柱样品的总探测效率,输出结果为能量点与其对应的探测效率。

|
图 7 耦合计算模块流程图 Figure 7 Flow diagram of coupling computing module |
在相同计算条件下,使用THUDose软件的蒙卡模拟方法和耦合方法分别进行无源效率刻度计算,以蒙卡方法结果为基准,将耦合方法的结果与以其进行比较,验证方法的精确性。本节中蒙卡模拟的单能量点粒子数为106,统计误差均小于5%。此外,还给出了耦合方法的积分次数和计算时间,与蒙卡模拟的计算时间进行了比较及优劣分析。
2.3.1 不同样品精确性验证以某单开端同轴HPGe探测器为例,将7类样品均置于探测器上表面中轴线上方100 mm处进行探测效率计算,与THUDose蒙卡模拟得到的探测效率刻度结果曲线比对如图8,样品的参数设置见表1。
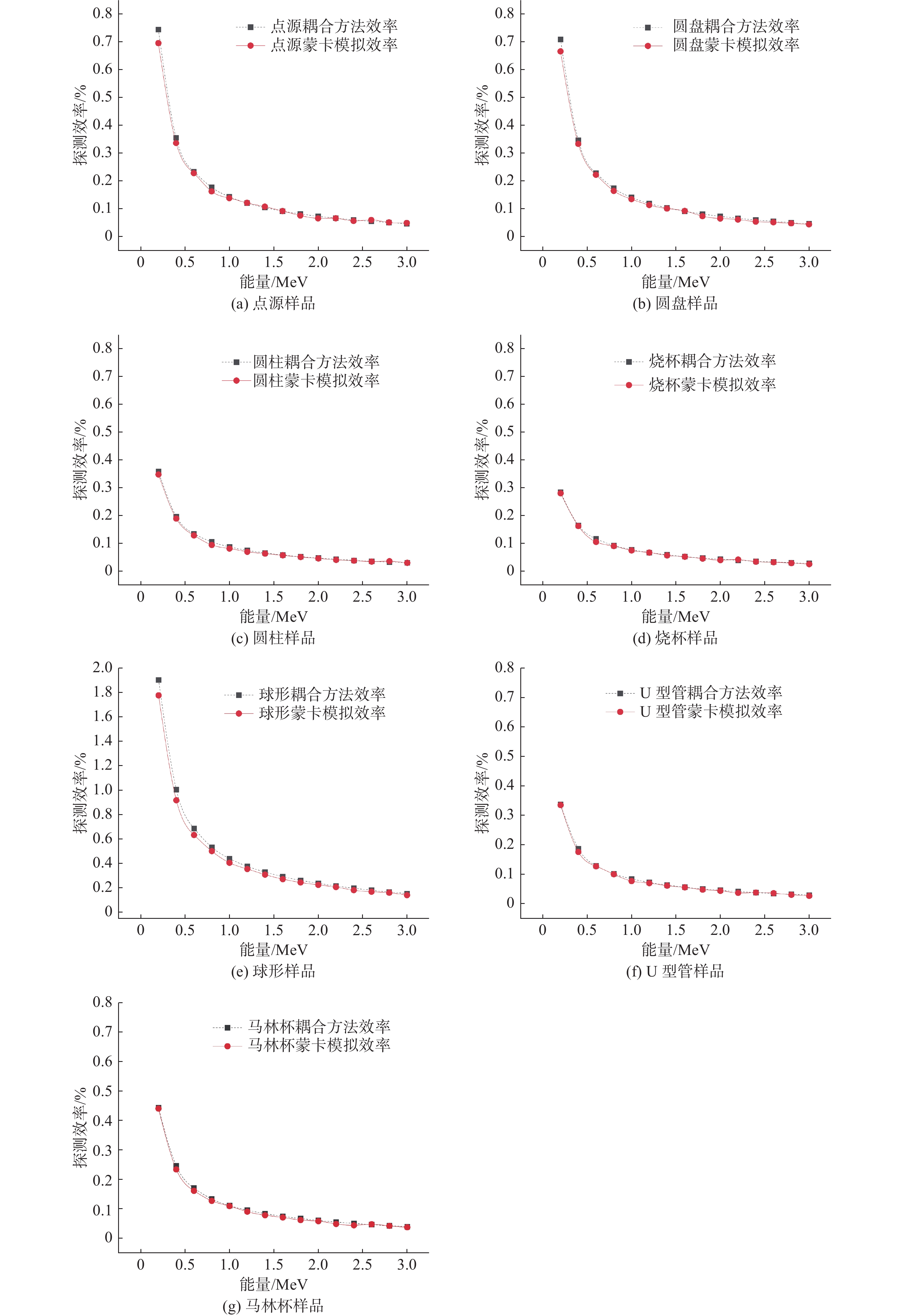
|
图 8 7类样品效率刻度曲线 Figure 8 Efficiency calibration curves of seven samples |
|
|
表 1 7类样品参数设置 Table 1 Parameters of seven samples |
由图8可知,样品模型中既有简单的如点源样品也有复杂的如U型管样品,本文提出的耦合方法均能较为精确地对其进行刻度,表2给出了耦合方法与THUDose模拟得到的效率的相对偏差,可以看出且对大部分能量的γ射线和样品模型相对偏差都小于10%。
|
|
表 2 7类样品耦合方法探测效率与蒙卡模拟偏差比较 Table 2 Comparison of detection efficiency deviation between coupling method and Monte Carlo simulation of seven samples |
对精确性的影响验证以圆柱样品为例,分别计算了样品位于探测器上表面中轴线上方100 mm和20 mm,以及上表面100 mm且水平方向偏离中轴线14.14 mm 3种情况的探测效率,并与THUDose的模拟结果进行比对,分析样品位置对计算精确性的影响。圆柱样品均采用半径21 mm、高41 mm、容器壁厚1 mm的模型,容器材料为铜,样品材料为水,探测效率刻度结果如图9。

|
图 9 不同位置圆柱样品效率刻度曲线 Figure 9 Efficiency calibration curves of cylindrical samples at different positions |
表3给出了不同位置圆柱样品效率刻度曲线计算偏差,大部分相对偏差在10%以内,因此认为本文提出的耦合方法能够较为精确地刻度圆柱样品的探测效率。在γ射线能量较低时,相对偏差较小,耦合方法比较精确;在γ射线能量大于2 MeV以上时,由于高能量的γ射线探测效率较低,导致相对偏差较大。
|
|
表 3 不同位置圆柱样品效率刻度曲线相对偏差 Table 3 Relative deviation of efficiency calibration curves of cylindrical samples at different positions |
对比样品置于探测器正上方100 mm和20 mm的计算结果,发现20 mm处的探测效率相对偏差普遍大于100 mm处且均大于5%,这表明样品探测效率的计算精度与样品距探测器上表面距离有关,距离探测器越近,耦合方法的精确性越低。综合分析样品的探测效率数据以及耦合方法的原理,认为上述偏差增加是由探测器表面的面积微元以及样品的体积微元由分割得来所致:当样品距离探测器上表面越近时,分割的面积微元、体积微元本身的面积、体积对比样品与探测器上表面的距离越不能忽视,从而导致积分计算结果偏差增大。
2.4 计算时间分析表4展示了耦合方法的数值积分次数、数值积分时间以及THUDose的蒙卡模拟的计算时间,计算平台为一台windows个人工作站,配有2颗Intel Xeon E5-2637 V4的4核CPU及64 GB内存。数值积分计算采用单核计算15个能量点,不同样品所需积分次数不同,样品模型越复杂,积分次数越多,用时越长;对于体源样品,积分次数的计算方法为:探测器上表面面积微元个数×样品体积微元个数(本文所用算例为3000×2700)。
|
|
表 4 数值积分方法与蒙卡方法计算用时对比 Table 4 Comparison of calculation time between numerical integration method and Monte Carlo method |
THUDose蒙卡模拟使用双核并行,共计算15个能量点,每个能量点计算106个粒子,总粒子数为1.5×107,平均每种样品用时都在7 min左右。
经过对比认为耦合方法相较于纯粹的蒙卡模拟能极大地提升无源效率刻度速度,且数值积分大部分计算均在探测器表面进行,若能事先在获得探测效率网格的步骤中完成这一过程,将能继续缩短无源效率刻度花费的时间。
2.5 实际应用将一台ORTEC公司生产的某型号HPGe γ谱仪送交中国计量科学研究院进行校准。校准过程中对241Am、60Co、40K等多类标准点源的γ射线进行了全能峰效率刻度。基于此建立了该HPGe γ谱仪的探测器模型,并使用耦合方法和THUDose蒙卡模拟对相应的γ射线进行了无源效率刻度。刻度结果如图10,点源距探头上表面25 cm,位于探头上表面中心正上方。
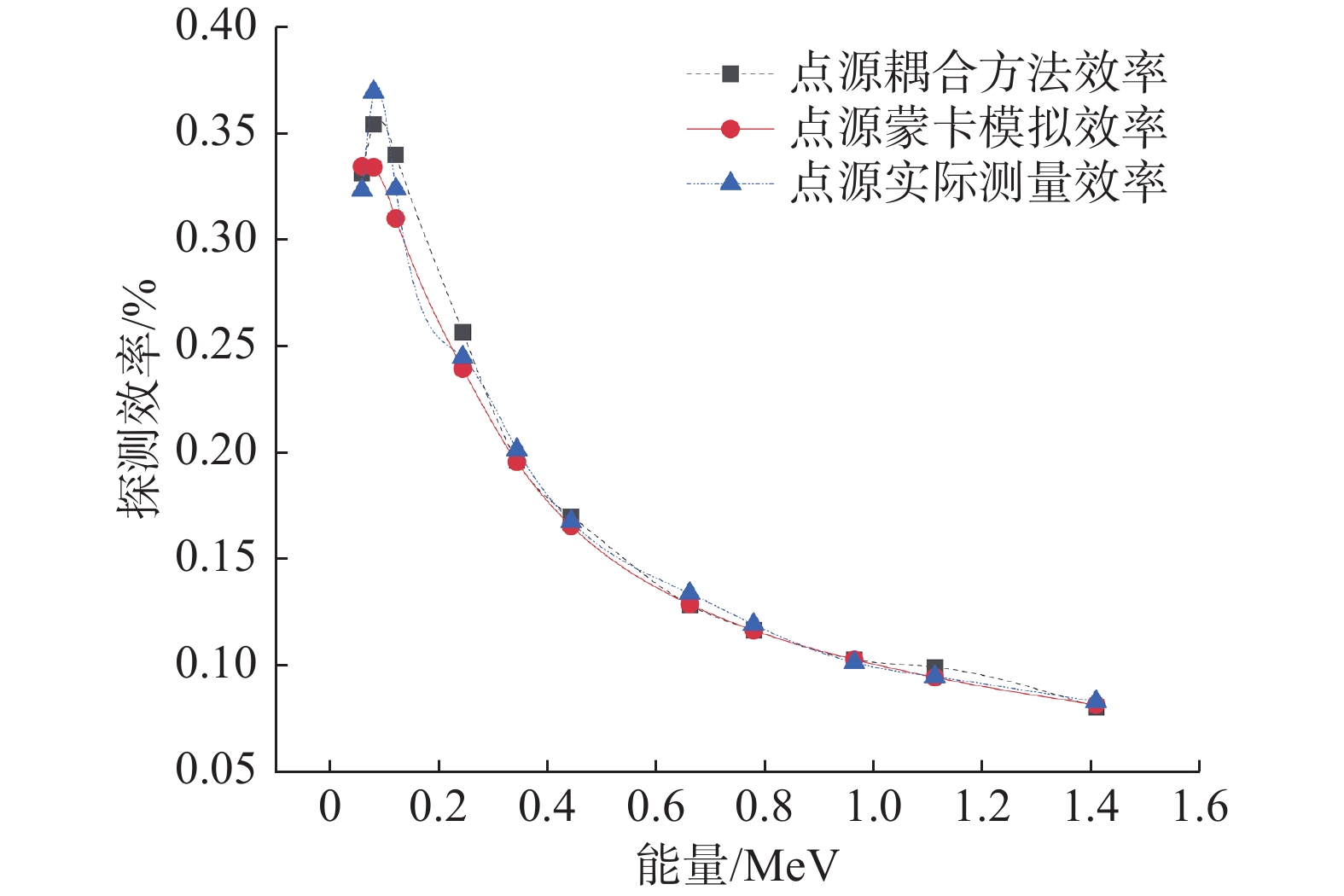
|
图 10 通过3类方法绘制的点源效率刻度曲线 Figure 10 Point source efficiency calibration curves with three methods |
由图10可知,耦合方法与THUDose蒙卡模拟得到的效率刻度曲线除低能区外,在形状上均能与实际测量曲线吻合。表5给出了耦合方法和蒙卡模拟的效率刻度曲线相对实际测量曲线的偏差,两者均在10%以内,认为2种方法均能较为准确地进行无源效率刻度,且耦合方法与蒙卡模拟的准确性相差不大。
|
|
表 5 耦合方法与蒙卡模拟相对实际测量的相对偏差 Table 5 Relative deviation of the coupling method and the Monte Carlo simulation compared with the actual measurement |
本文基于前人研究基础,建立了一种适用于多种常用样品的蒙卡与解析耦合无源效率刻度计算方法,该方法在保留蒙卡模拟精确性的基础上,结合解析计算速度快的优点,能精准快速地完成无源效率刻度工作。
耦合方法对于不同种类的样品计算得到的探测效率与蒙卡方法相对偏差大部分在10%以内,计算时间均缩短了至少7倍;同时在实际应用中与有源效率刻度得到的点源探测效率相对偏差0.33%~9.53%。这与商用无源效率刻度软件LabSOCS相近,曾奕等[13]使用LabSOCS对152Eu点源进行无源效率刻度的结果偏差在0.03%~9.2%;李奇等[14]使用LabSOCS对152Eu、133Ba、60Co点源进行无源效率刻度的结果偏差在0.3%~5.6%。上述比较表明耦合方法具有形成软件投入实际应用的价值。
目前耦合方法还存在样品与探测器距离过近刻度不准、无法对不规则几何样品进行刻度等局限性。在本文基础上,还可从并行计算、微元划分、大样品及不规则样品效率计算等方面进行优化和扩展,改进方法的计算速度、精度及适用性,从而进一步提升其在实际无源效率刻度应用中的工程实用价值。
| [1] |
陈立, 马豪, 曾志, 等. 基于蒙特卡罗的HPGe伽马谱仪无源效率刻度方法[J]. 强激光与粒子束, 2013, 25(1): 201-206. Chen L, Ma H, Zeng Z, et al. Monte Carlo-based sourceless efficiency calibration method of HPGe γ spectrometer[J]. High Power Laser Part Beams, 2013, 25(1): 201-206. DOI:10.3788/HPLPB20132501.0201 |
| [2] |
丁洪林, 张秀凤. 半导体探测器及其应用[M]. 北京: 原子能出版社, 1989: 1-48. Ding HL, Zhang XF. Semiconductor detector and its application[M]. Beijing: Atomic Energy Press, 1989: 1-48. |
| [3] |
安继刚. 致电离辐射探测学讲义(上册)[M]. 北京: 清华大学出版社, 1993: 199-256. An JG. Ionizing radiation detection[M]. Beijing: Tsinghua University Publishing House Co. , Ltd, 1993: 199-256. |
| [4] |
杨悦. 高纯锗γ谱仪体源效率刻度方法的对比研究及应用[D]. 南昌: 东华理工大学, 2019: 7-13. Yang Y. Approaches for efficiency calibration of volume source with HPGe γ-ray spectrometry: comparative study and application[D]. Nanchang: East China University of Technology, 2019: 7-13. |
| [5] |
付杰, 徐翠华. 无源效率刻度技术研究进展及应用概况[J]. 核电子学与探测技术, 2007, 27(4): 799-804. Fu J, Xu CH. Research and application of sourceless efficiency calibration technic[J]. Nucl Electron Detect Technol, 2007, 27(4): 799-804. DOI:10.3969/j.issn.0258-0934.2007.04.047 |
| [6] |
Badawi MS, Gouda MM, Nafee SS, et al. New algorithm for studying the effect of self attenuation factor on the efficiency of γ-rays detectors
[J]. Nucl Instrum Methods Phys Res A, 2012, 696: 164-170. DOI:10.1016/j.nima.2012.08.089 |
| [7] |
Badawi MS, Gouda MM, Nafee SS, et al. New analytical approach to calibrate the co-axial HPGe detectors including correction for source matrix self-attenuation[J]. Appl Radiat Isot, 2012, 70(12): 2661-2668. DOI:10.1016/j.apradiso.2012.08.014 |
| [8] |
Saegusa J, Oishi T, Kawasaki K, et al. Determination of gamma-ray efficiency curves for volume samples by the combination of Monte Carlo simulations and point source calibration[J]. J Nucl Sci Technol, 2000, 37(12): 1075-1081. DOI:10.1080/18811248.2000.9714994 |
| [9] |
Venkataraman R, Bronson F, Atrashkevich V, et al. Improved detector response characterization method in ISOCS and LabSOCS[J]. J Radioanal Nucl Chem, 2005, 264(1): 213-219. DOI:10.1007/s10967-005-0696-7 |
| [10] |
王硕, 杨宝路, 周强, 等. 无源效率刻度在马林杯状气体源活度测量中的应用[J]. 中国辐射卫生, 2022, 31(1): 6-12. Wang S, Yang BL, Zhou Q, et al. Application of sourceless efficiency calibration in activity measurement of gas source in Marinelli beaker[J]. Chin J Radiol Health, 2022, 31(1): 6-12. DOI:10.13491/j.issn.1004-714X.2022.01.002 |
| [11] |
赖忠俊, 宣志强, 俞顺飞, 等. 有源-无源γ能谱分析方法在分析环境样品中放射性核素的应用[J]. 中国辐射卫生, 2020, 29(4): 378-381,386. Lai ZJ, Xuan ZQ, Yu SF, et al. Application of sources and sources-less methods of γ spectrometry for analysis of radionuclides in environmental sample[J]. Chin J Radiol Health, 2020, 29(4): 378-381,386. DOI:10.13491/j.issn.1004-714X.2020.04.014 |
| [12] |
罗熹宇, 邱睿, 武祯, 等. 辐射防护设计与剂量计算软件THUDose的研发与应用[J]. 现代应用物理, 2021, 12(2): 23-28. Luo XY, Qiu R, Wu Z, et al. Development and application of radiation protection calculation software THUDose[J]. Mod Appl Phys, 2021, 12(2): 23-28. DOI:10.12061/j.issn.2095-6223.2021.020203 |
| [13] |
曾奕, 徐彬, 陈立. 实验室无源效率刻度技术的准确性检验[J]. 四川环境, 2011, 30(3): 5-9. Zeng Y, Xu B, Chen L. Calibration check for efficiency scale of sourceless detection in laboratory[J]. Sichuan Environ, 2011, 30(3): 5-9. DOI:10.3969/j.issn.1001-3644.2011.03.002 |
| [14] |
李奇, 王世联, 樊元庆, 等. 无源效率刻度在活度测量中的应用研究[J]. 核电子学与探测技术, 2013, 33(5): 568-571. Li Q, Wang SL, Fan YQ, et al. Application of sourceless efficiency calibration in activity measurement[J]. Nucl Electron Detect Technol, 2013, 33(5): 568-571. DOI:10.3969/j.issn.0258-0934.2013.05.011 |




