烟囱等通风管道内气载流出物的取样监测需保证气体样品的代表性,相关标准建议在管道内气体流速及示踪物质分布较为均匀的截面上,采用单点取样器采集气体样品[1-2]。因此需预先对管道内部各截面位置的混合均匀性进行验证。除现场实验外,多采用比例模型实验或计算流体力学(CFD)仿真的方法,进行通风管道内气体混合均匀性问题研究[3-4]。
随着控制方程数值解法的不断改进及计算硬件水平的提高,CFD仿真已经可以部分取代物理实验,完成通风管道内气体混合规律的探索,并且具有较高的效率和求解精度[5-6]。针对某一特定管道结构,McFarland等通过模型实验证实了,当管道内部流场处于完全发展的湍流状态后,增大雷诺数对于气体混合均匀性的提高无明显作用,同时也排除了模型尺寸的影响[7-8];Seo等针对4种典型结构的通风管道开展实验测量,进一步指出管道结构变化对于内部气体混合均匀性影响显著,且90°弯头引起的扰动会极大促进气体混合,并分析了流体的压力变化以解释这一现象[9]。
物理实验通常需耗费大量的时间及经济成本,且测量结果易受限于仪器精度[7-8]。本文通过仿真手段,研究截面分别为方形和圆形的长直管(I型)、90°单弯管(L型)、90°双弯管(S型和U型)内的速度分布及气体混合规律,其结论可作为通风管道设计的参考。
1 材料与方法基于有限体积法的通用CFD软件Fluent在对Navier-Stokes方程进行数值求解前,需确定边界条件并选择适宜的流动控制方程,并对流体区域进行离散化处理[10-11]。
通过雷诺数
| $ Re=\frac{\rho vD}{\mu } $ | (1) |
式中,
方形管截面尺寸
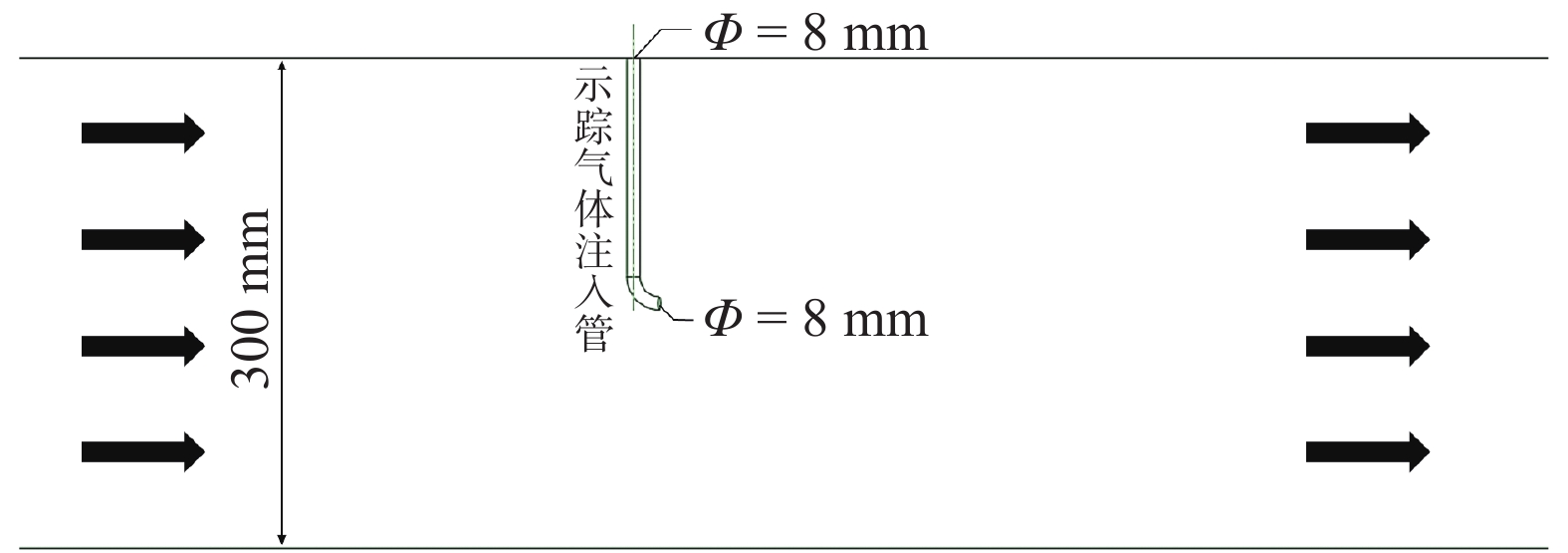
|
图 1 示踪气注入管尺寸及位置 Figure 1 The size and position of the tracer gas injection pipe |
管道内气体视为不可压缩流体,计算过程中密度
| $ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0 $ | (2) |
采用三维笛卡尔直角坐标系建立模型,
| $ \left\{\begin{array}{c}\dfrac{\partial \rho u}{\partial t}+\nabla \cdot \left(\rho u\overrightarrow{\mathit{v}}\right)={\rho F}_{x}-\dfrac{\partial p}{\partial x}+\mu \left(\dfrac{{\partial }^{2}u}{\partial {x}^{2}}+\dfrac{{\partial }^{2}u}{\partial {y}^{2}}+\dfrac{{\partial }^{2}u}{\partial {z}^{2}}\right)\\ \dfrac{\partial \rho \upsilon }{\partial t}+\nabla \cdot \left(\rho \upsilon \overrightarrow{\mathit{v}}\right)={\rho F}_{y}-\dfrac{\partial p}{\partial y}+\mu \left(\dfrac{{\partial }^{2}v}{\partial {x}^{2}}+\dfrac{{\partial }^{2}v}{\partial {y}^{2}}+\dfrac{{\partial }^{2}v}{\partial {z}^{2}}\right)\\ \dfrac{\partial \rho w}{\partial t}+\nabla \cdot \left(\rho w\overrightarrow{\mathit{v}}\right)={\rho F}_{z}-\dfrac{\partial p}{\partial z}+\mu \left(\dfrac{{\partial }^{2}w}{\partial {x}^{2}}+\dfrac{{\partial }^{2}w}{\partial {y}^{2}}+\dfrac{{\partial }^{2}w}{\partial {z}^{2}}\right)\end{array}\right. $ | (3) |
式中,
湍流过程的仿真调用标准形式的
由于空气与示踪气体混合前经历了3倍水力直径的扩散,理论上流速分布较为均匀,采用截面中心2/3以上面积内的速度变异系数COV表征速度分布均匀性;示踪气体注入后,混合初期集中于截面中心,2/3以上面积内的浓度COV较高,受湍流扩散及布朗运动影响,下游远距离处截面混合均匀性将逐渐提高[3,14-15]。
速度及示踪气体浓度变异系数COV定义为标准差与均值的比值,计算式为:
| $ COV=\frac{s}{\bar x}=\frac{1}{\bar x}\sqrt{\frac{1}{n-1}\sum\nolimits _{i=1}^{n}{({x}_{i}-{\bar x})}^{2}} $ | (4) |
式中,
截面为正方形及圆形时,水力直径D均为

|
图 2 I型长直管道几何示意 Figure 2 Geometric schematic diagram of long straight I-type pipe |
速度COV与截面位置(
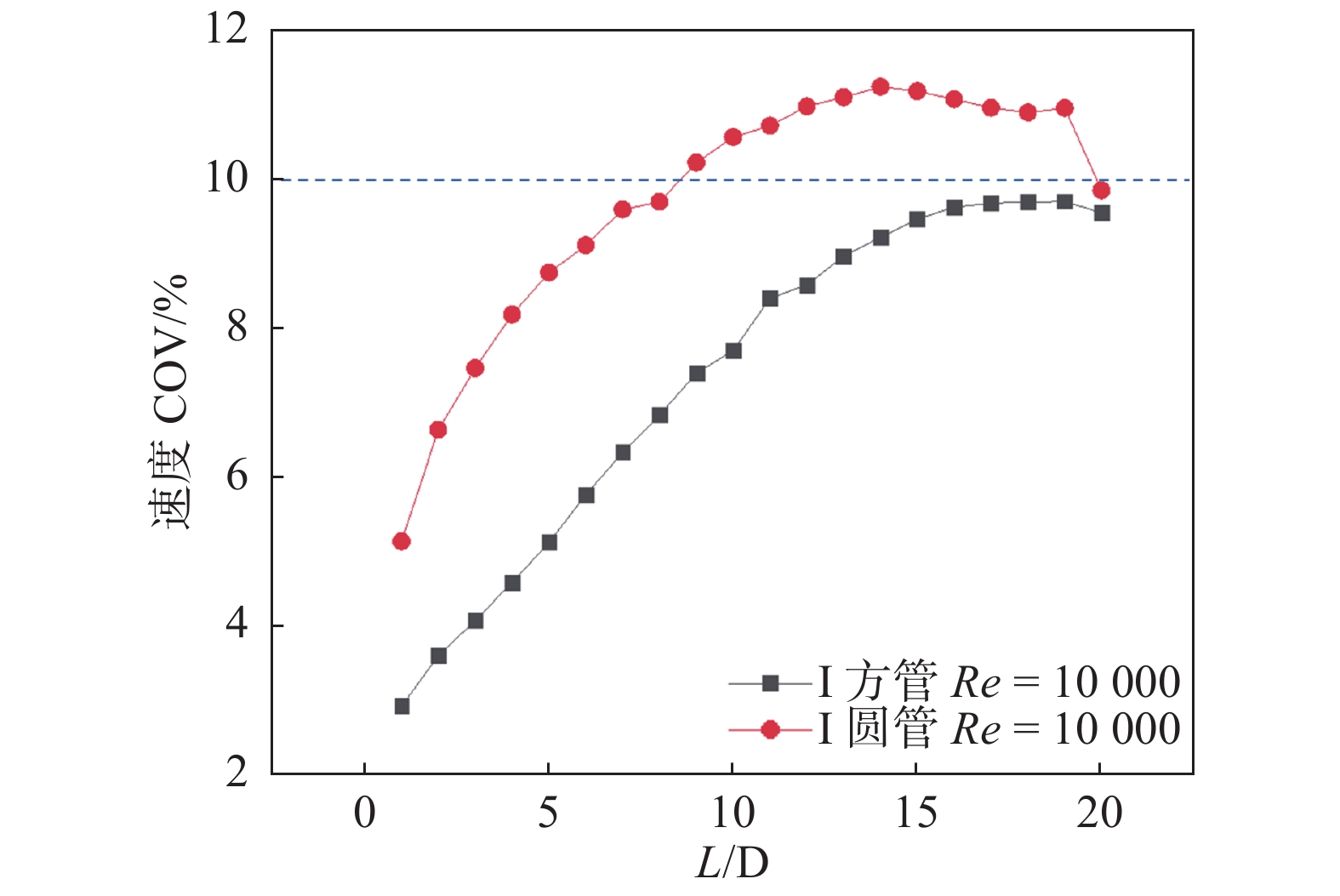
|
图 3 I型管道速度COV与截面位置关系 Figure 3 The relationship between velocity COV and section position in I-type pipe |
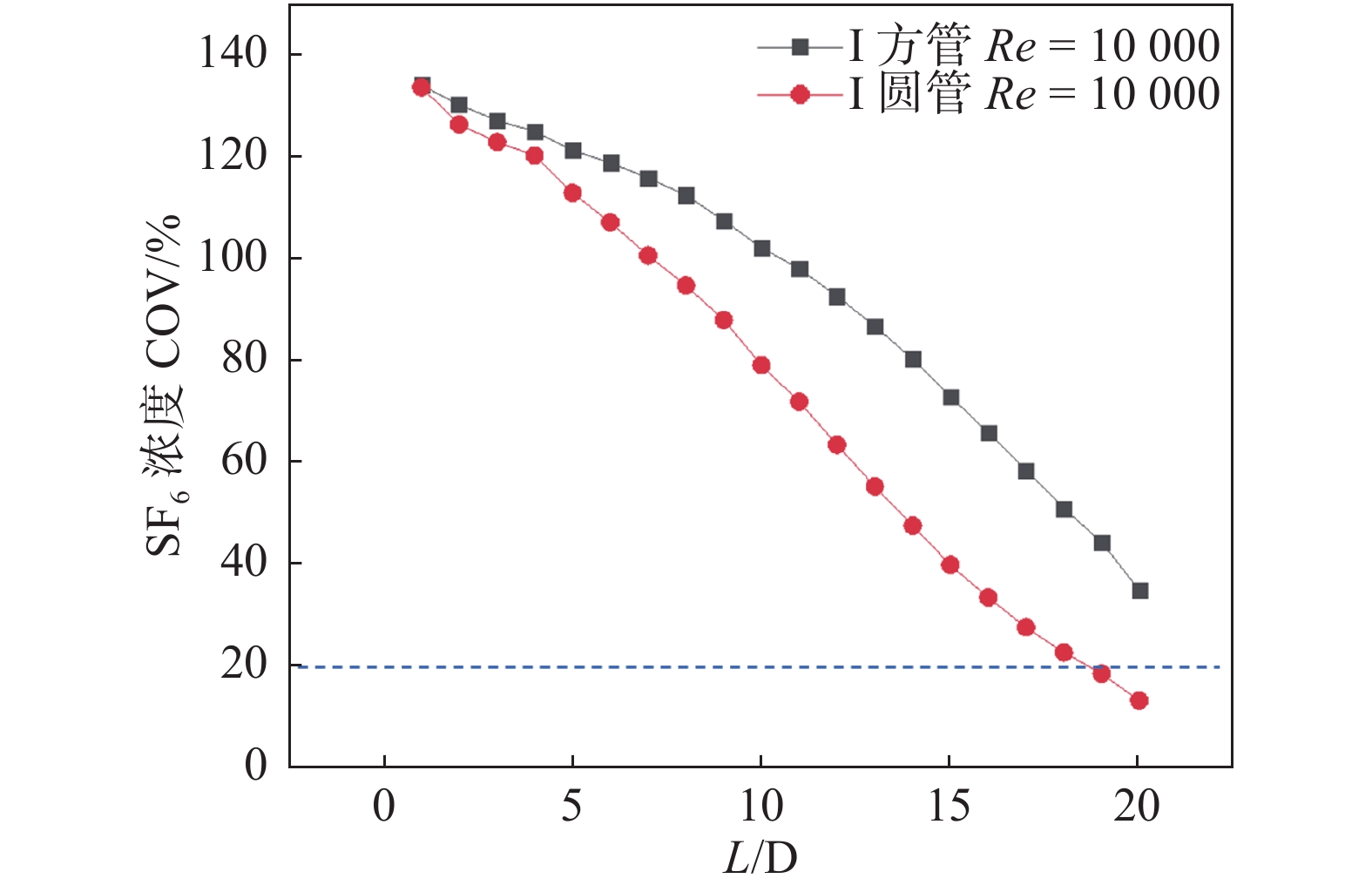
|
图 4 I型管道
|
长直管道缺乏结构变化带来的流场扰动,无法带来良好的混合效果[3,9],当管道截面为圆形,若要达到相关标准要求的混合均匀性指标,可能需要20倍水力直径的混合距离,对管道截面为方形,所需混合的距离可能更长,见图5。
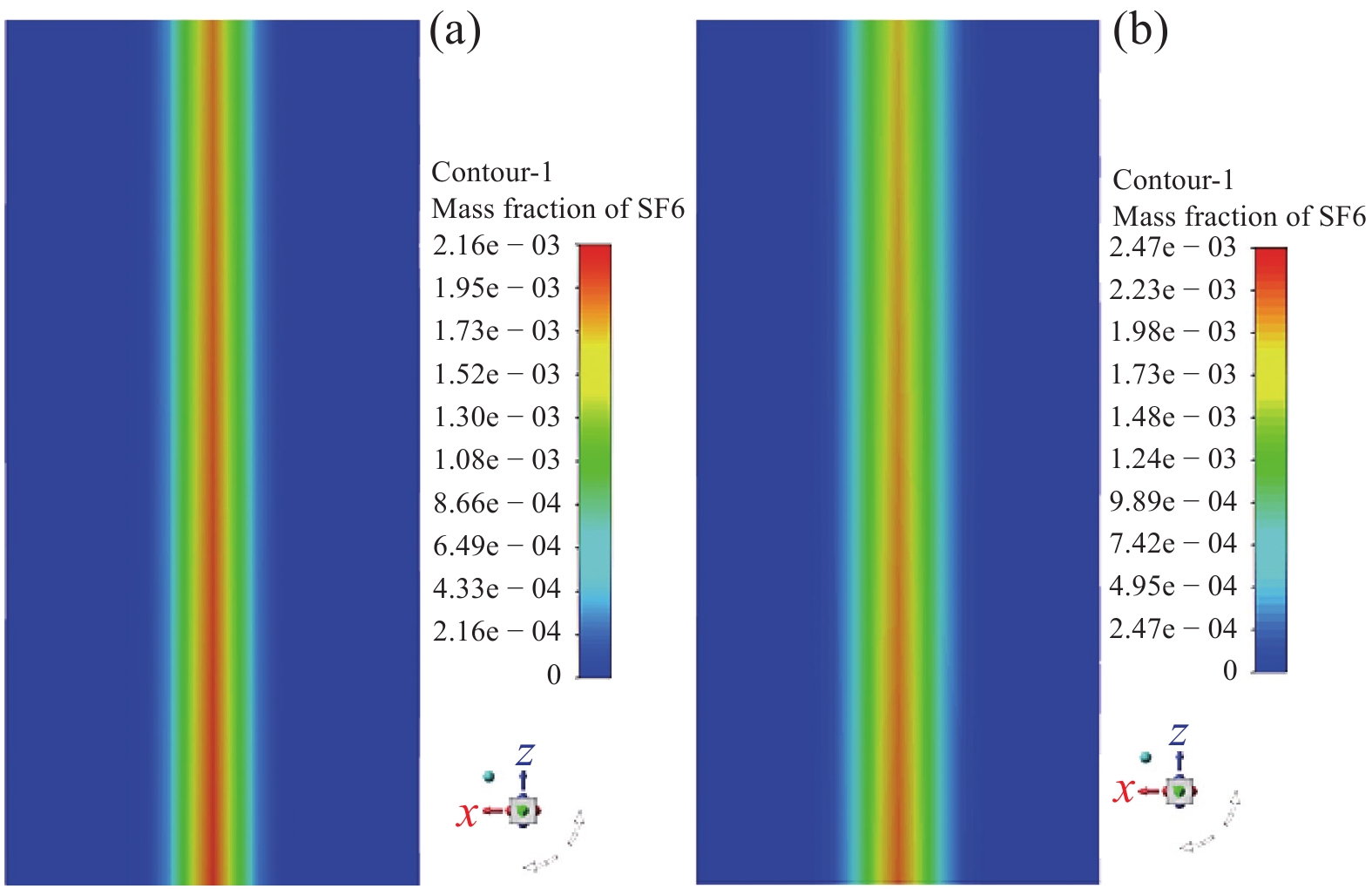
|
图 5 I型管道
|
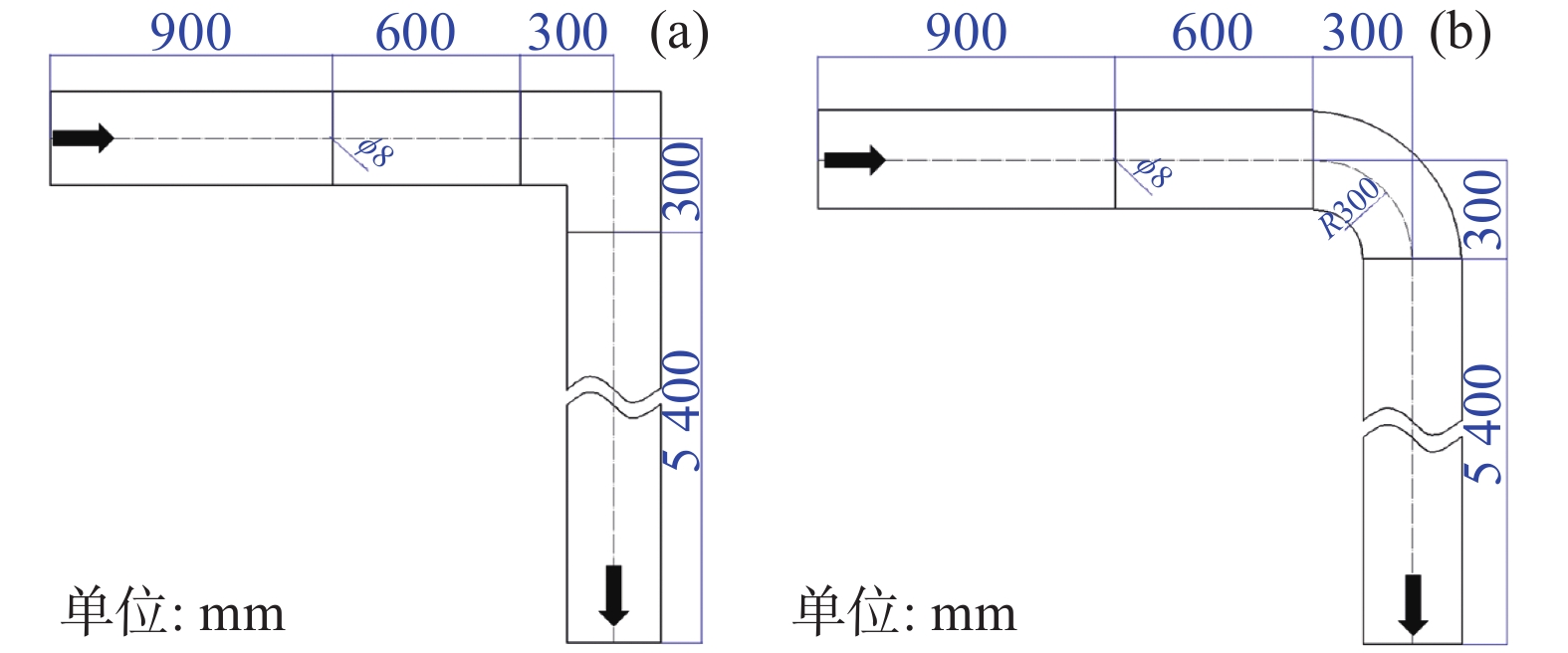
L型单弯头管道采用90°弯头连接两段直管,空气入口下游3倍水力直径设示踪气注入口,再经过2倍水力直径的直管段,90°弯头后接
|
图 6 L型单弯头管道几何示意(a为方形截面;b为圆形截面) Figure 6 Geometric schematic diagram of L-type single-bend pipe (a: square section; b: circular section) |
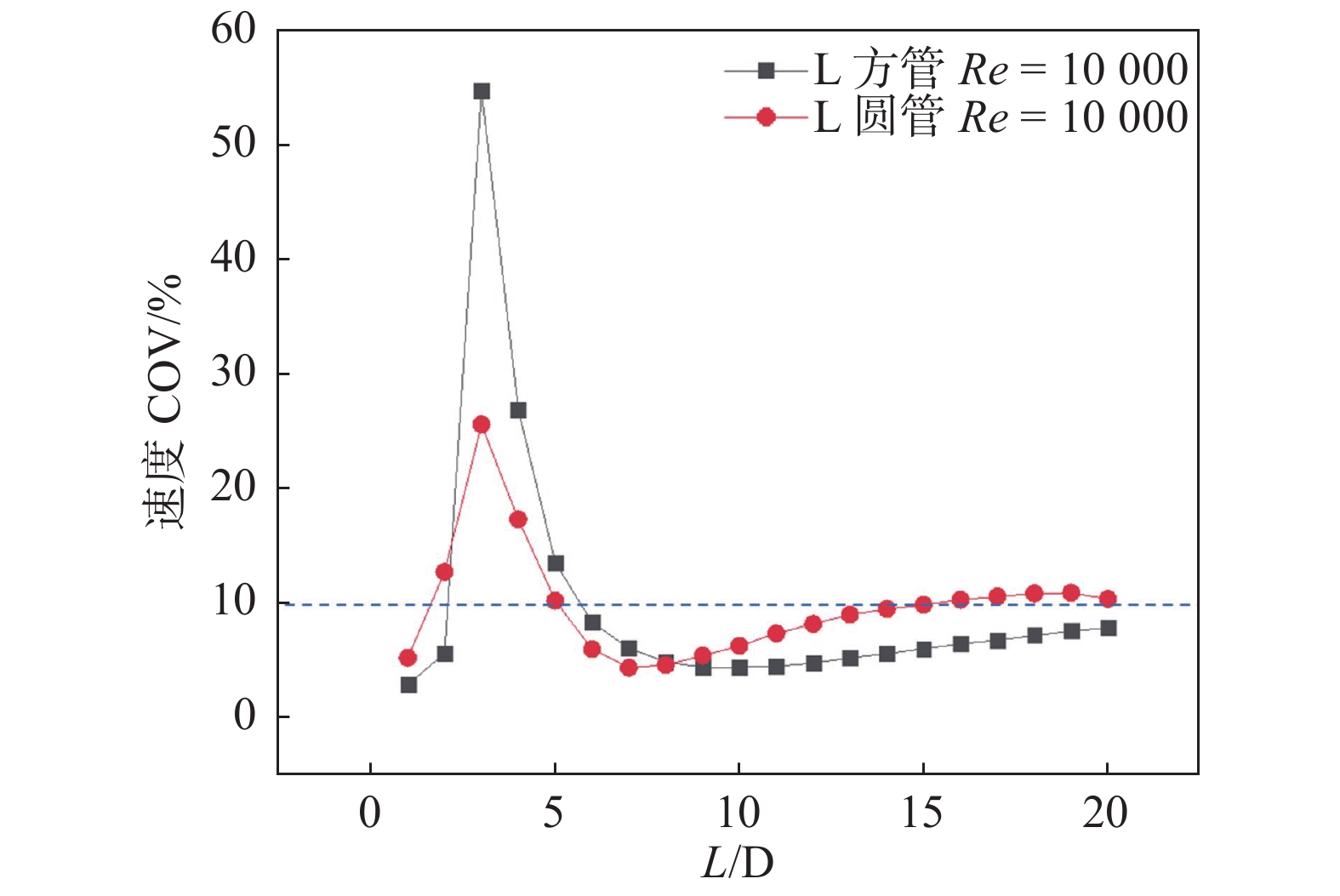
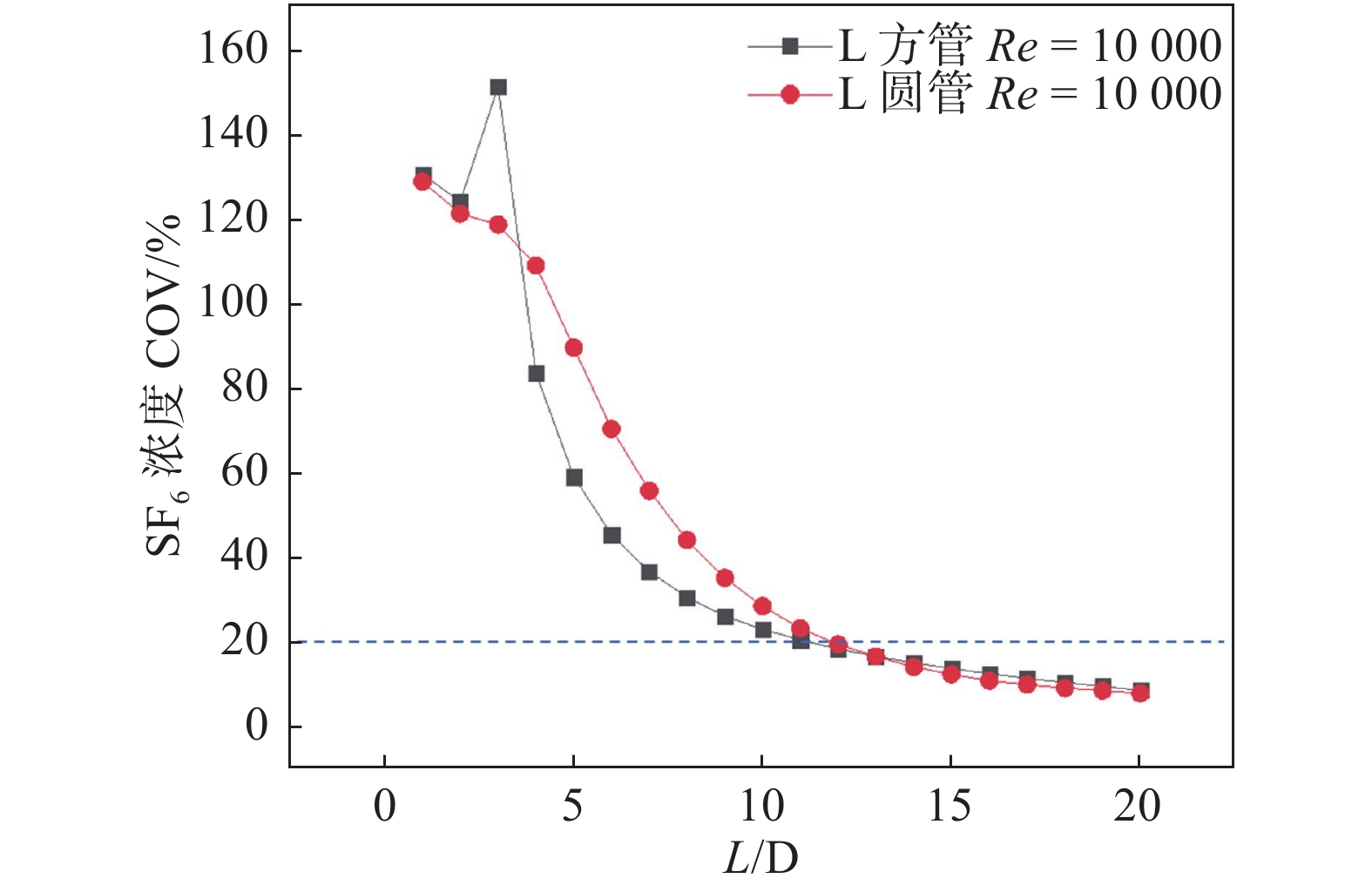
示踪气体先经2倍水力直径的直管混合,再受90°弯头的扰动后,继续监测18倍水力直径的直管段混合效果。速度COV与截面位置的关系见图7,示踪气体浓度COV与截面所在位置的关系见图8。
|
图 7 L型管道速度COV与截面位置关系 Figure 7 The relationship between velocity COV and section position in L-type pipe |
|
图 8 L型管道
|
2倍水力直径的直管段混合,速度COV有升高趋势,且圆形管更为明显,经历弯头后,第3个监测截面速度COV大幅升高,且方形管速度COV的波动更为剧烈,但在下游直管段,速度COV在较短距离有大幅下降,经9倍水力直径后,方形管内速度COV低于圆形管,其后有小幅升高的趋势,直到监测末端都保持均匀分布;
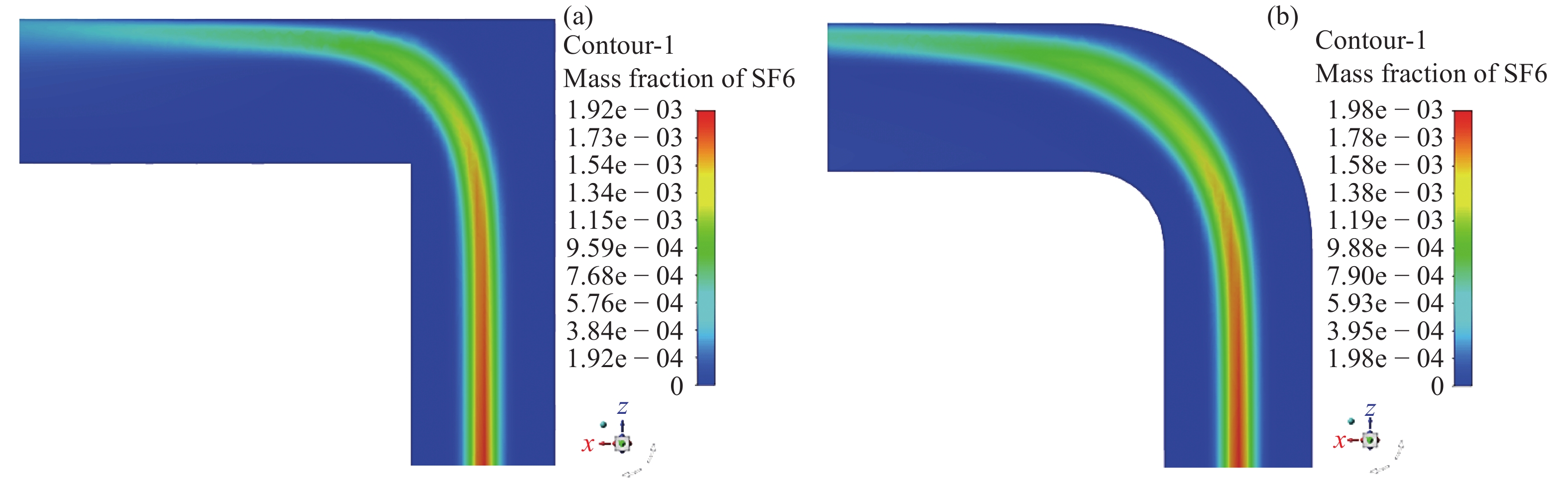
90°弯头引起的扰动可以极大促进示踪气体混合,且对于方形管道效果更为明显,虽然弯头下游短,距离内气体分布可能极不均匀,但后续混合效果提升显著,见图9。
|
图 9 L型管道
|
S型双弯头管道采用2个90°弯头连接3段直管,第1、3直管段内气流方向相同,两弯头之间为2倍水力直径的直管,第3段直管长
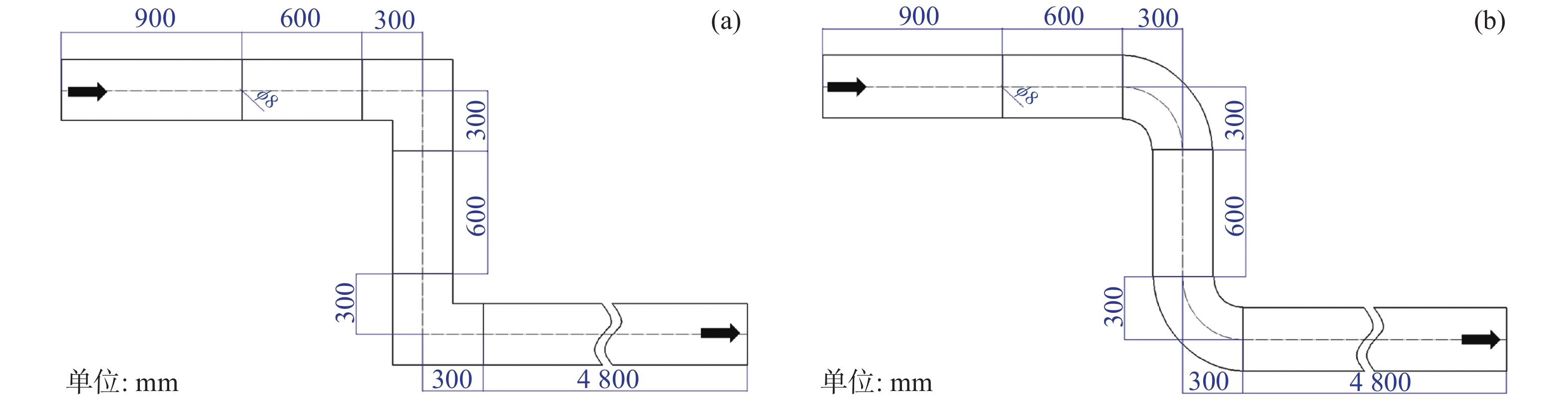
|
图 10 S型双弯头管道几何示意(a为方形截面;b为圆形截面) Figure 10 Geometric schematic diagram of S-type double-bend pipe (a: square section; b: circular section) |
第1直管段内包含2个监测截面,两弯头间的第2直管段包含2个监测截面,第3直管段内设置16个监测截面。S型双弯头管道20个截面的速度COV与截面位置的关系见图11,示踪气体浓度COV与截面所在位置关系见图12。
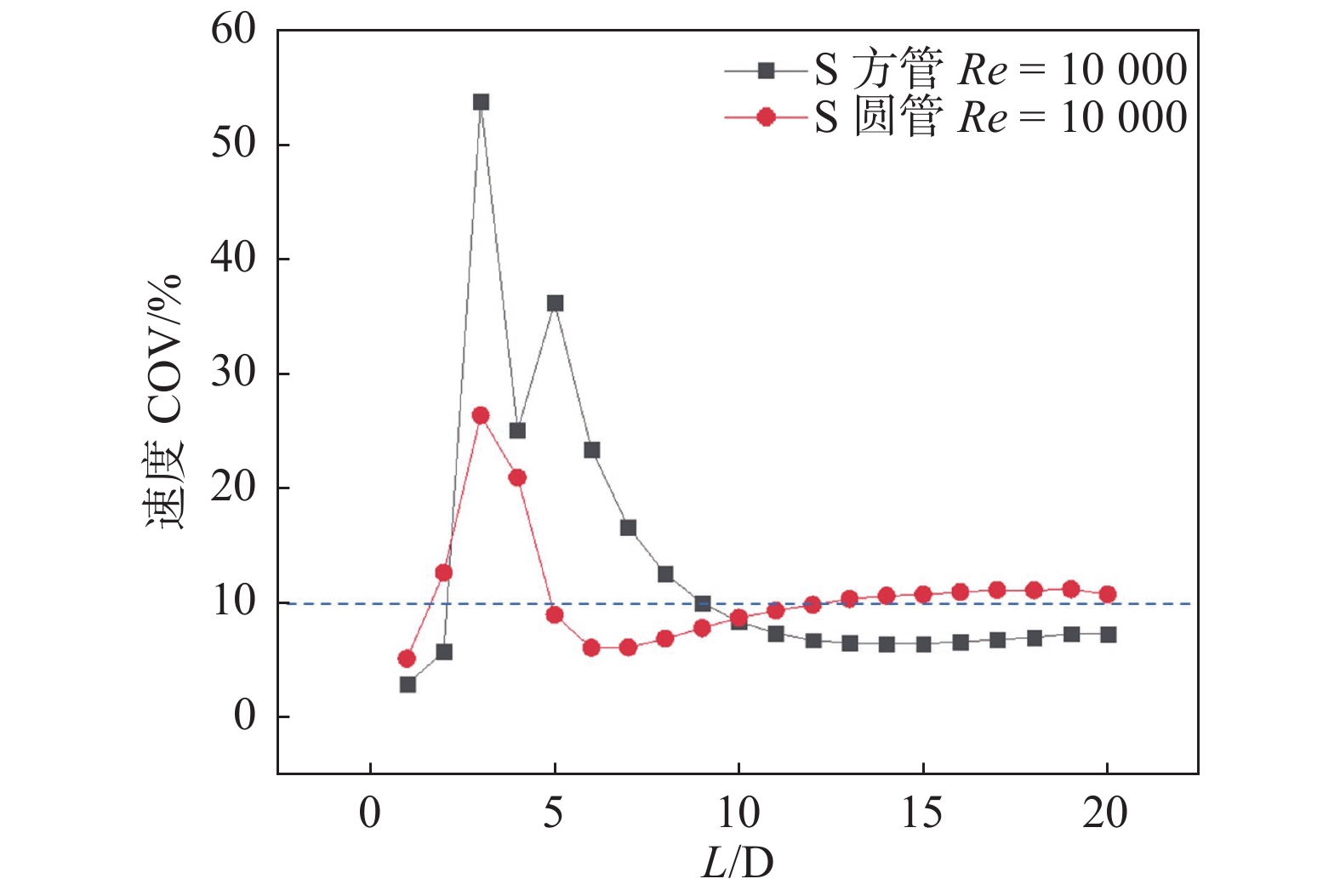
|
图 11 S型管道速度COV与截面位置关系 Figure 11 The relationship between velocity COV and section position in S-type pipe |
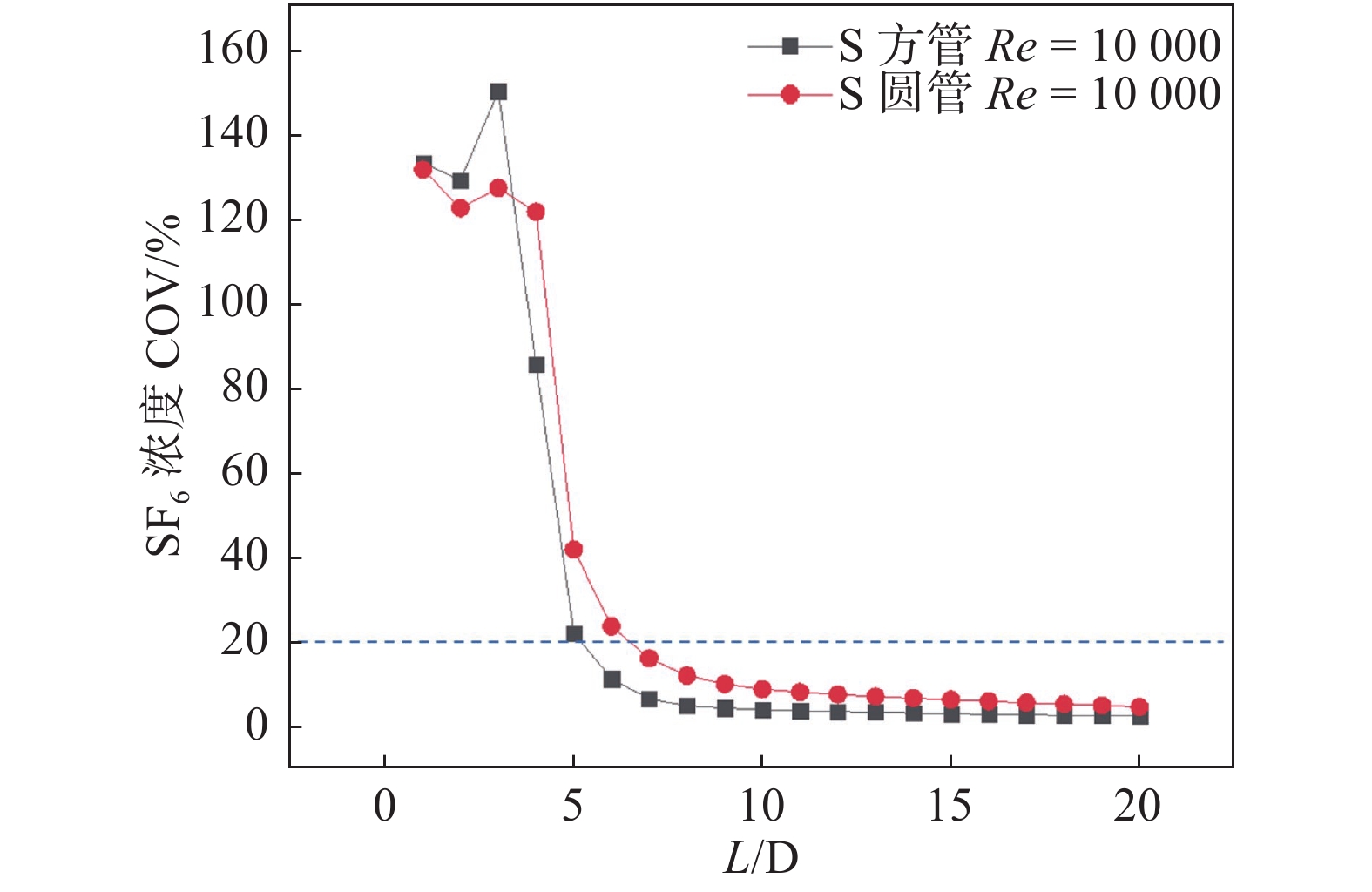
|
图 12 S型管道
|
类似于L型单弯头管道,经历第一个90°弯头后,方形和圆形管内的速度COV均有大幅增加,均匀性变差,但气体流经第2个弯头后,圆形管速度COV未表现出波动,在5倍水力直径位置的截面,方形管速度COV为36%,圆形管则低于10%,且3~9倍水力直径范围内,圆形管内的速度分布更为均匀,而10倍水力直径之后,情况相反;对于
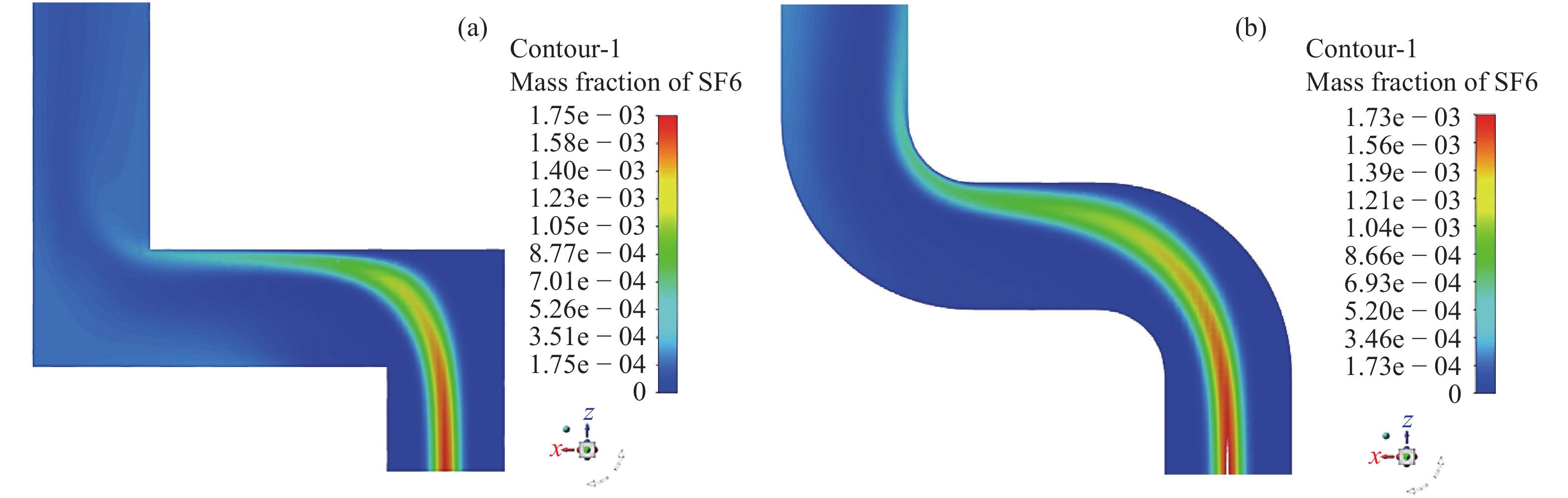
|
图 13 S型管道
|
综合速度与示踪气体的统计数据,方形S管道在7倍水力直径后满足了气体混合的均匀性,圆形管同样也需7倍水力直径的混合距离,但方形弯头的扰动效果强于圆形弯头,这与Seo团队的实验结果较为一致[9]。
2.4 U型双弯头管速度及气体混合均匀性分析U型双弯头管道采用2个90°弯头连接3段直管,第1、3直管段内气流方向相反,两弯头之间为2倍水力直径的直管,第3段直管长
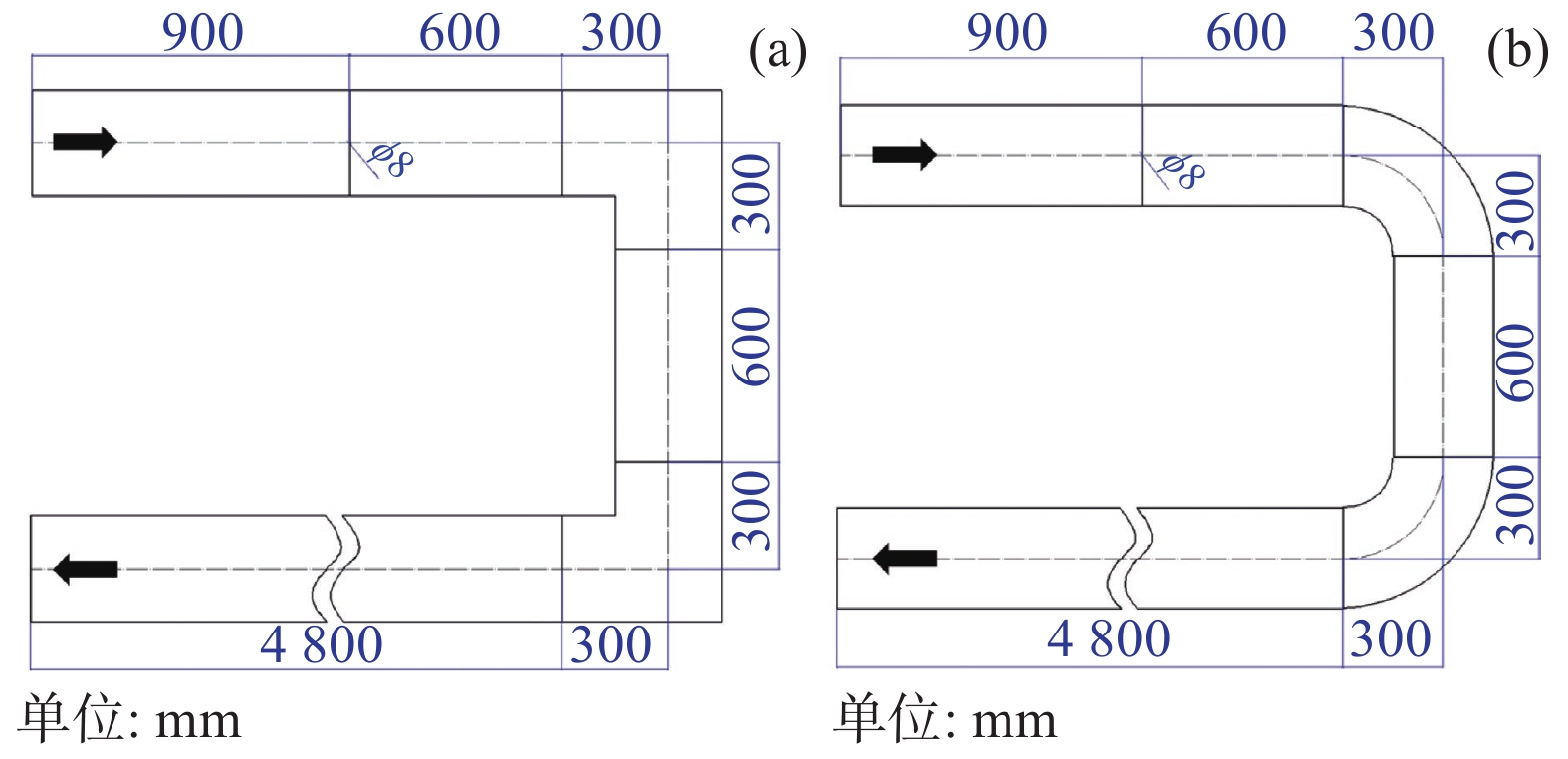
|
图 14 U型双弯头管道几何示意(a为方形截面;b为圆形截面) Figure 14 Geometric schematic diagram of U-type double-bend pipe (a: square section; b: circular section) |
方形及圆形截面的U型双弯头管道20个截面的速度COV、示踪气体浓度COV与截面位置(
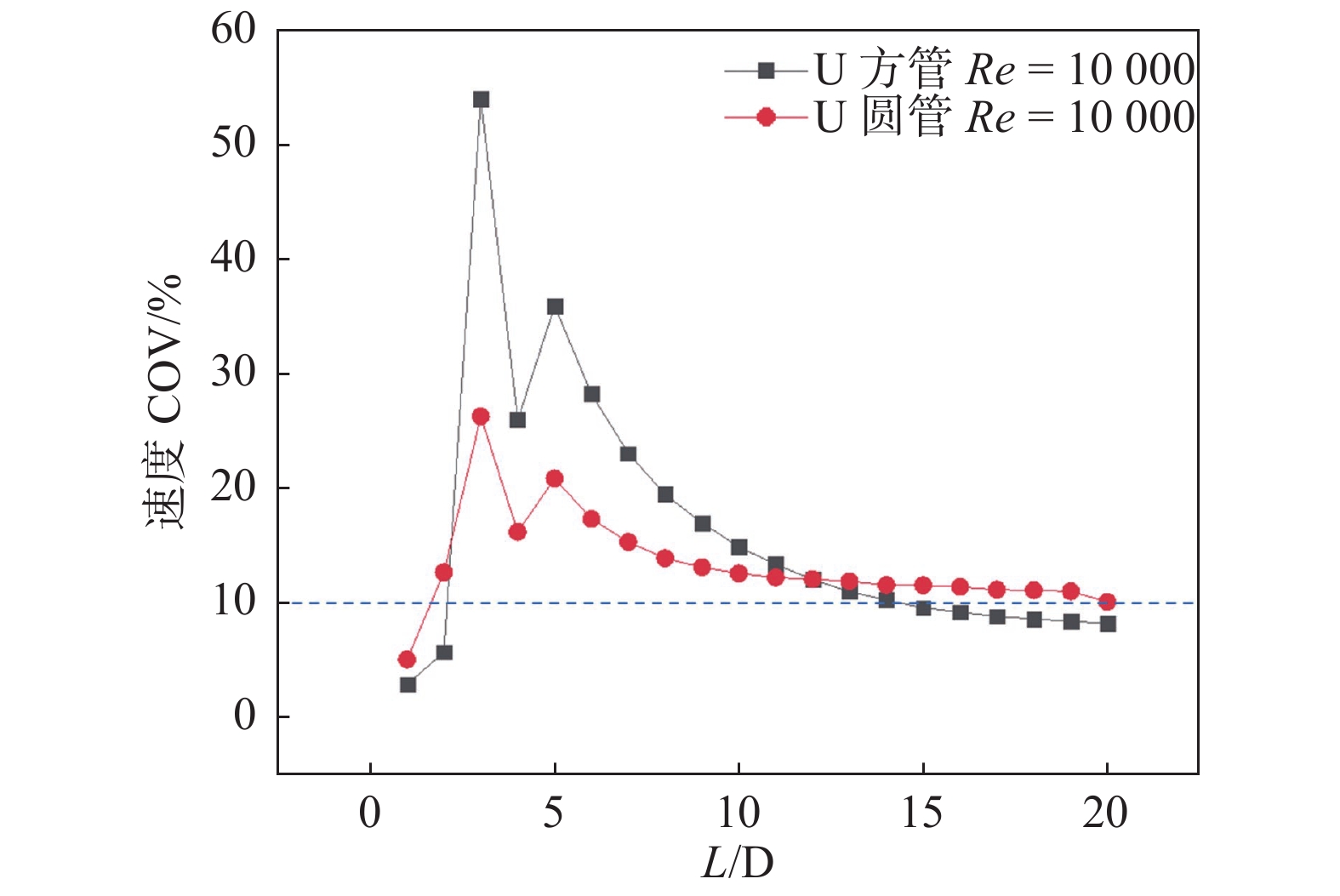
|
图 15 U型管道速度COV与截面位置关系 Figure 15 The relationship between velocity COV and section position in U-type pipe |

|
图 16 U型管道
|
不同于S型双弯头管,当气体流经第2个弯头后,圆形和方形管4倍水力直径和5倍水力直径位置,截面速度COV均出现了增大,但依然是方形管波动较大,圆管与方管分别在4倍水力直径和8倍水力直径后达到了速度COV < 20%,下游12倍水力直径后,方形管速度 COV略低于圆管,且降低的趋势更为陡峭;
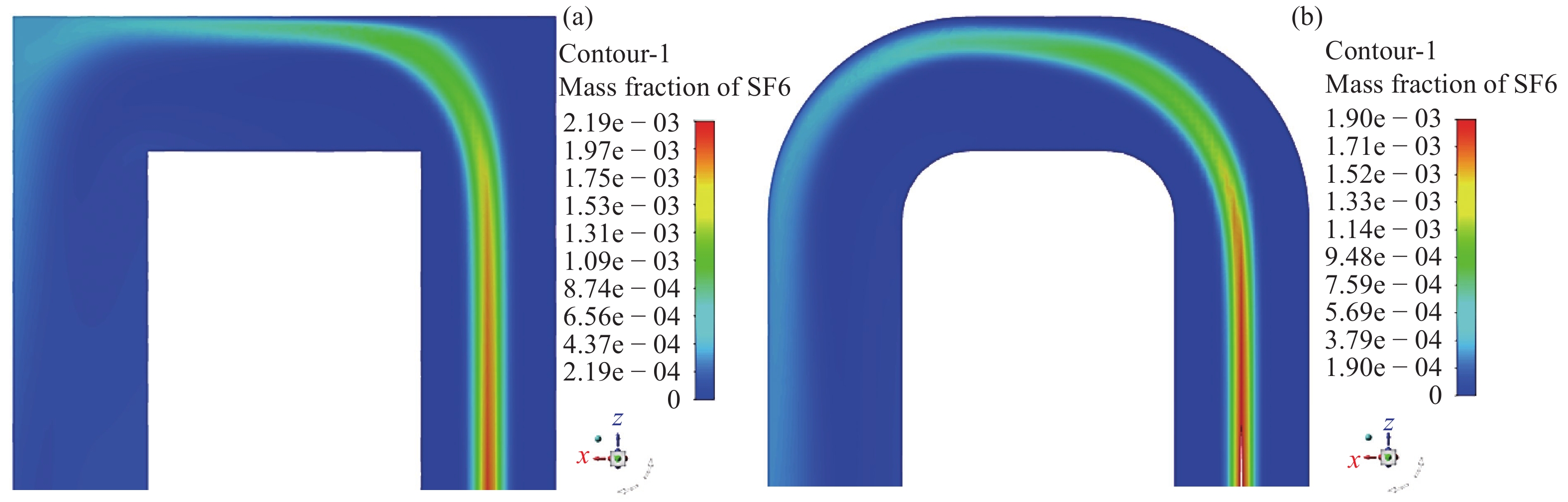
|
图 17 U型管道
|
对于圆形截面的U型管道,示踪气体的混合效果欠佳,弯头部分的平滑过渡带来的导流作用可能远比扰动作用显著[7-9,16],而具有相同水力直径的方形管在8倍水力直径后满足了速度分布和示踪气体浓度的均匀性。
2.5 雷诺数对速度及气体混合均匀性影响一般情况下,通风设施尺寸较大,内部气体流动均能保证充分的湍流状态[3,17-18],前述的仿真过程中,主管道内的雷诺数均为10000。选择方形截面的4种管道,再次设定入口边界条件,使流动雷诺数达到50000,并与雷诺数2 000的状态对比,验证雷诺数对于此4种管道结构的影响情况。
4种结构的管道在3种雷诺数条件下,速度COV变化趋势见图18。
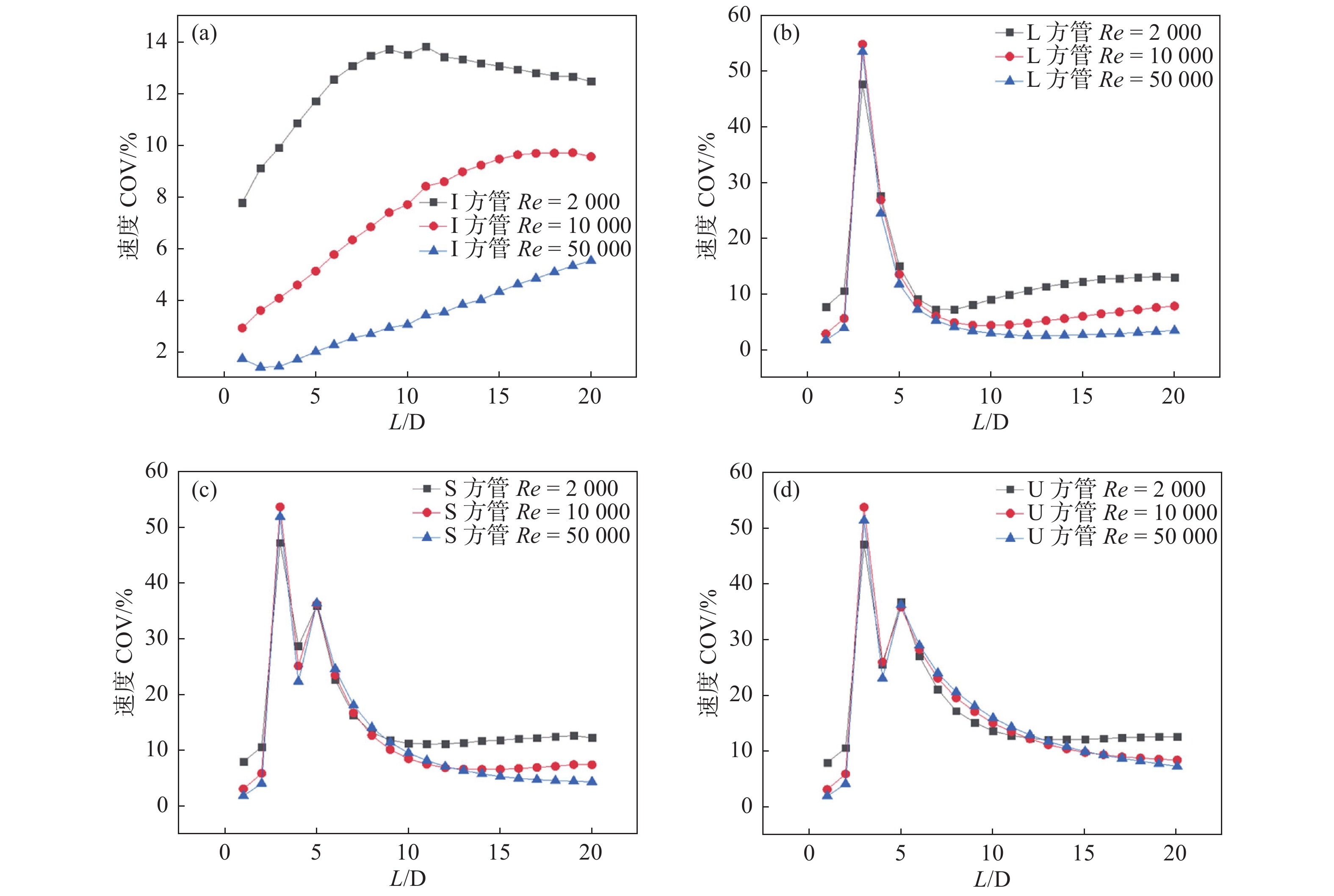
|
图 18 4种管道结构的速度COV与截面位置关系(a为I型;b为L型;c为S型;d为U型) Figure 18 The relationship between velocity COV and section position for four pipe structures (a: I type; b: L type; c: S type; d: U type) |
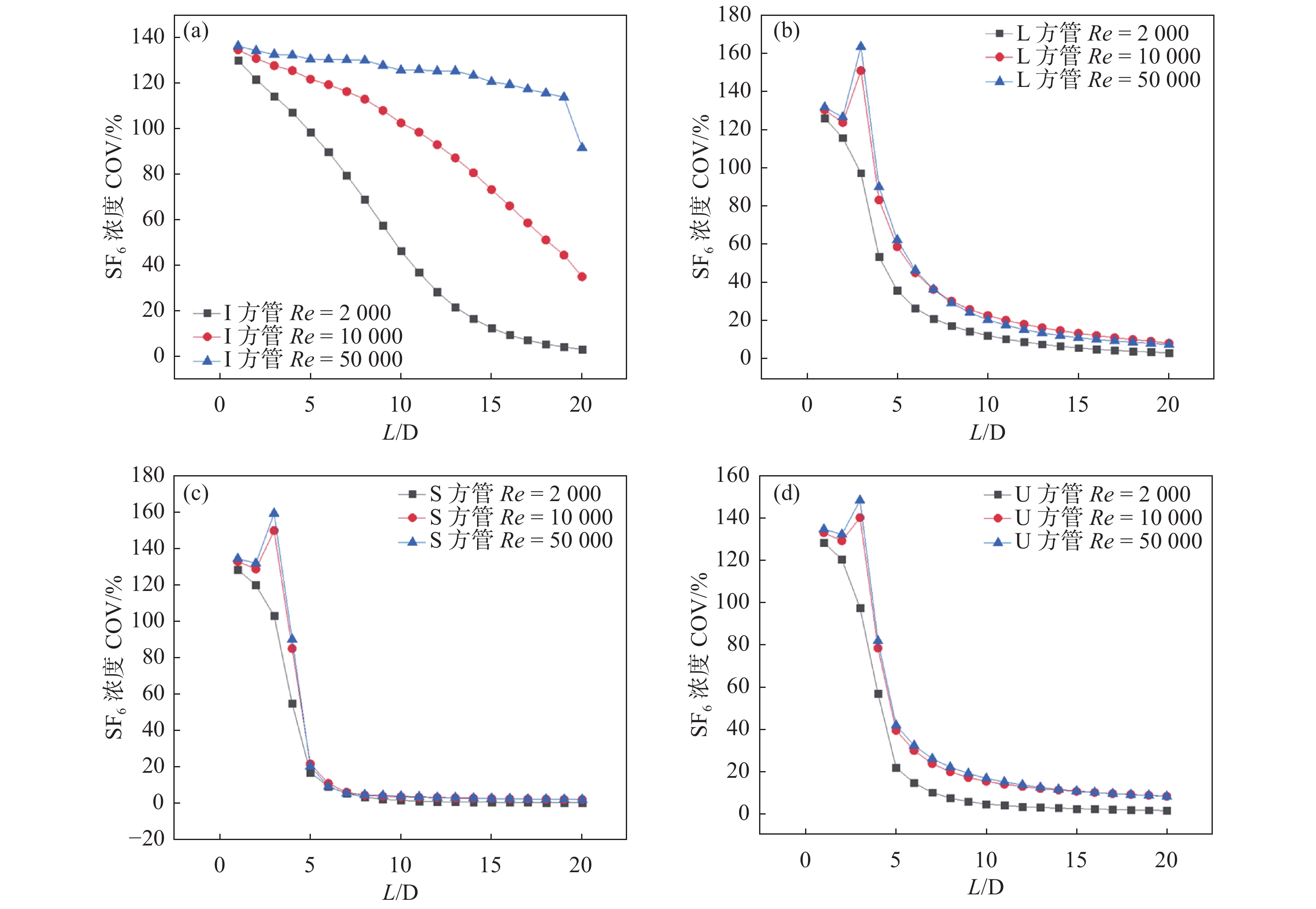
I型长直管道内的速度COV在3种雷诺数条件下均能满足标准要求的20%以下,随Re增大,速度COV有所增加,但充分的湍流状态下,伴随监测截面向下游移动,速度COV呈现了先增大后减小的结果;对于L型、S型和U型管道,3种雷诺数条件下的速度COV变化趋势都较为接近,Re为10000及50000时的曲线走势极其相似,在弯头处的波动程度也更大。
4种管道结构在3种雷诺数下的示踪气体浓度COV变化趋势见图19。
|
图 19 四种管道结构的
|
由图可知,雷诺数较低,无法达到充分的湍流,示踪气体遇到90°弯管的扰动时,混合效果不会有明显的变化。长直管道在雷诺数较低时,示踪气体混合得更为快速,13倍水力直径满足了均匀性要求,而湍流状态下,大的雷诺数反而可能降低混合的效果;对于L型、S型和U型管道,湍流雷诺数条件下的示踪气体浓度COV变化趋势都较为接近,经历弯头的扰动后,示踪气体将以更快的速度混合均匀。
3 讨 论通过计算流体力学的仿真,研究截面分别为方形和圆形的长直管(I型)、90°单弯管(L型)、90°双弯管(S型和U型)内的速度分布及气体混合情况,得出以下结论:1)对于气体而言,同样的布置形式,方形管道比圆形管道具有更好的混合效果,其在弯头及转角等部位可产生更为强烈的扰动作用。2)长直管道内的气体需要经历极长距离的输运扩散才能达到较好的混合均匀性,而在管道中增加弯头,对于降低速度和示踪气体浓度COV,效果十分显著。3)相比于L型单弯头管道,S型和U型双弯头管道能在更短距离内实现气体的均匀混合,可节约至少4倍水力直径的混合距离。4)方形截面的S型管道与U型管道在示踪气体混合方面性能接近,但U型管道第2个弯头带来的COV值波动可能更为明显。5)当管道内流场处于充分的湍流后,雷诺数对于速度及示踪气体浓度COV的影响不再重要,继续提高雷诺数对于混合均匀性提升无益。6)Mcfarland等的实验证实,要达到混合均匀性指标,单弯头直管段至少需7倍水力直径的混合距离,双弯头直管段则至少4倍水力直径,流场充分湍流后,继续提高雷诺数无益[3,7-9]。计算流体力学方法可模拟通风管道内的气体迁移混合过程,并获得较为可靠的结果。
| [1] |
卢正永. 核设施烟囱和管道气载放射性排放物的取样监测——美国新标准介绍(三)[J]. 辐射防护通讯, 2003, 23(3): 40-42. Lu ZY. Sampling and monitoring releases of airborne radioactive substances from the stacks and ducts of nuclear facilities—introduction of a new standard of the America: part III[J]. Radiat Prot Bull, 2003, 23(3): 40-42. DOI:10.3969/j.issn.1004-6356.2003.03.008 |
| [2] |
ISO. ISO 2889—2010 Sampling airborne radioactive materials from the stacks and ducts of nuclear facilities[S]. Switzerland: [s.n.], 2010: 110.
|
| [3] |
Anand M, McFarland AR, Rajagopal KR. Gas mixing for achieving suitable conditions for single point aerosol sampling in a straight tube: experimental and numerical results[J]. Health Phys, 2003, 84(1): 82-91. DOI:10.1097/00004032-200301000-00007 |
| [4] |
Zhang HF, Ahmadi G. Aerosol particle transport and deposition in vertical and horizontal turbulent duct flows[J]. J Fluid Mech, 2000, 406: 55-80. DOI:10.1017/S0022112099007284 |
| [5] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 33582—2017 机械产品结构有限元力学分析通用规则[S]. 北京: 中国标准出版社, 2017: 14. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration. GB/T 33582—017 General principles of structural finite element analysis for mechanical products[S]. Beijing: Standards Press of China, 2017: 14. |
| [6] |
Schwer LE. An overview of the PTC 60/V&V 10: guide for verification and validation in computational solid mechanics[J]. Eng Comput, 2007, 23(4): 245-252. DOI:10.1007/s00366-007-0072-z |
| [7] |
McFarland AR, Anand NK, Ortiz CA, et al. A generic mixing system for achieving conditions suitable for single point representative effluent air sampling[J]. Health Phys, 1999, 76(1): 17-26. DOI:10.1097/00004032-199901000-00004 |
| [8] |
McFarland AR, Gupta R, Anand NK. Suitability of air sampling locations downstream of bends and static mixing elements[J]. Health Phys, 1999, 77(6): 703-712. DOI:10.1097/00004032-199912000-00015 |
| [9] |
Seo Y. Degree of mixing downstream of rectangular bends and design of an inlet for ambient aerosol[D]. Texas: Texas A&M University, 2004.
|
| [10] |
钱丛昊. 燃煤电厂排放烟气流速与气体污染物排放量测量方法的研究[D]. 南京: 东南大学, 2019. Qian CH. Research on measurement method of flue gas velocity and gas pollutant emission from coal-fired power plants[D]. Nanjing: Southeast University, 2019. |
| [11] |
董信芳, 李航, 丁世海, 等. “华龙一号”核电厂烟囱气态流出物取样系统验证的试验与分析[J]. 中国辐射卫生, 2018, 27(1): 52-57. Dong XF, Li H, Ding SH, et al. Verification for the representative sampling system of “Hualong I” NPP gaseous effluent: test and analysis[J]. Chin J Radiol Health, 2018, 27(1): 52-57. DOI:10.13491/j.cnki.issn.1004-714X.2018.01.014 |
| [12] |
叶涛. 多组分粉体混合过程的理论分析与实验研究[D]. 武汉: 武汉理工大学, 2009. Ye T. Theoretical analysis and experimental study for process of multicomponent powders mixing[D]. Wuhan: Wuhan University of Technology, 2009. |
| [13] |
程攀攀, 王海宁, 梅力, 等. 颗粒粉尘在水平管道内运移的三维数值模拟[J]. 环境工程学报, 2017, 11(10): 5457-5464. Cheng PP, Wang HN, Mei L, et al. 3D simulation on transporting of particle dust in horizontal duct[J]. Chin J Environ Eng, 2017, 11(10): 5457-5464. DOI:10.12030/j.cjee.201612149 |
| [14] |
Kelbaliev GI, Ibragimov ZI, Kasimova RK. Deposition of aerosol particles in vertical channels from an isotropic turbulent flow[J]. J Eng Phys Thermophys, 2010, 83(5): 908-916. DOI:10.1007/s10891-010-0413-4 |
| [15] |
Yin ZQ, Li XF, Bao FB, et al. Thermophoresis and Brownian motion effects on nanoparticle deposition inside a 90° square bend tube[J]. Aerosol Air Qual Res, 2018, 18(7): 1746-1755. DOI:10.4209/aaqr.2018.02.0047 |
| [16] |
Dai ZP, Yin ZQ. Flow and deposition characteristics of nanoparticles in a 90° square bend[J]. Thermal Sci, 2015, 19(4): 1235-1238. DOI:10.2298/TSCI1504235D |
| [17] |
杨光俊, 丁力, 郭照冰. 基于CFD方法的燃煤电厂烟气排放数值模拟[J]. 环境科学研究, 2017, 30(12): 1934-1943. Yang GJ, Ding L, Guo ZB. Numerical simulation of flue gas emissions from coal-fired power plants using computational fluid dynamics method[J]. Res Environ Sci, 2017, 30(12): 1934-1943. DOI:10.13198/j.issn.1001-6929.2017.03.51 |
| [18] |
陈建利, 王洪凯, 李建发, 等. 核电厂通风系统中压差测量问题分析及解决建议[J]. 中国辐射卫生, 2019, 28(4): 433-435,439. Chen JL, Wang HK, Li JF, et al. Analysis and solution of the differential pressure measurement problem in the ventilation systems of nuclear power plants[J]. Chin J Radiol Health, 2019, 28(4): 433-435,439. DOI:10.13491/j.issn.1004-714X.2019.04.023 |



