核事故后果评价是事故应急决策的重要支持手段,源项信息的准确度直接影响到核事故后果评价及应急决策,其中源项的不确定性是造成评价结果误差的主要原因之一[1]。为获得较准确的核事故源项,基于监测数据反演事故释放源项的技术得到广泛发展。源项反演基本原理是将各个测量点坐标、测量数据以及气象数据(如大气稳定度、风向、风速、温度)与大气扩散模型相结合,从而推导出源项。文中基于环境监测数据和高斯烟羽模型,分析比较了可用于源项反演的几种优化算法,并对同条件下不同算法计算结果的准确性进行比较验证,初步研究了放射性释放源项反演模型。
1 材料和方法 1.1 扩散模型高斯烟羽模型结构简单,所需计算参数少,计算迅速,能够快速估算出烟羽的大概分布,扩散因子计算见式1)[2],反演过程见式2):
| $\begin{array}{l} {{C}}({\rm{x}},{{y}},{\text{z}},{{H}}) = \dfrac{{{A}}}{{{\rm{2}}{\text{π}} {\sigma _y}{\sigma _{\text{z}}}{\rm{u}}}}\exp \left[ { - \dfrac{1}{2}{{\left( {\dfrac{y}{{{\sigma _y}}}} \right)}^2}} \right]\\ \left\{ {\exp \left[ { - \dfrac{1}{2}{{\left( {\dfrac{{{\text{z}} - H}}{{{\sigma _{\text{z}}}}}} \right)}^2}} \right] + \exp \left[ { - \dfrac{1}{2}{{\left( {\dfrac{{{\text{z}} + H}}{{{\sigma _{\text{z}}}}}} \right)}^2}} \right]} \right\} \exp \left( { - \dfrac{{\lambda x}}{u}} \right)DF\left( x \right) \end{array} $ | (1) |
| $\begin{gathered} X*A = Y \\ \left[ {\begin{array}{*{20}{c}} {{x_{1,1}}}&{{x_{1,2}}}&{...}&{{x_{1,n}}} \\ {{x_{2,1}}}&{{x_{2,2}}}&{...}&{{x_{2,n}}} \\ {...}&{}&{}&{...} \\ {{x_{p,1}}}&{{x_{p,2}}}&{...}&{{x_{p,n}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{a_1}} \\ {{a_2}} \\ {...} \\ {{a_n}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{y_1}} \\ {{y_2}} \\ {...} \\ {{y_p}} \end{array}} \right] \\ \end{gathered} $ | (2) |
式中,C为时间积分的空气浓度,(Bq·s)/m3;A为释放量,Bq;H为有效释放高度,m;λ为核素衰变系数,s−1;x,y,z均为计算点坐标,m;σy,σz分别为横向和纵向扩算参数,m;u为有效释放高度H处的平均风速,m/s;DF(x)为烟羽耗减因子。xi,j为i点j时段的弥散因子,由扩散公式计算;aj为j时段的释放量;yi为i点在n时刻(高斯模型n = 1)的监测值。
1.2 优化算法目前优化算法主要使用的有最小二乘法、禁忌搜索算法、遗传算法和蚁群优化算法等[3-5]。
(1)最小二乘法:该算法通过最小化误差的平方和寻找数据的最佳函数匹配,简便地求得未知数据,并使所得数据与实际数据之间误差的平方和为最小。具体过程分3步:① 确定线性方程组X * A = Y,X为p × n矩阵,p ≥ n,A为[a1,a2,…,an]T,Y为[y1,y2,…,yn]T;② 分别计算XT * X,XT * Y;③ 计算A = XT * Y/XT * X。流程见图1。

|
图 1 最小二乘法计算流程图 Figure 1 Flow chart of least square method |
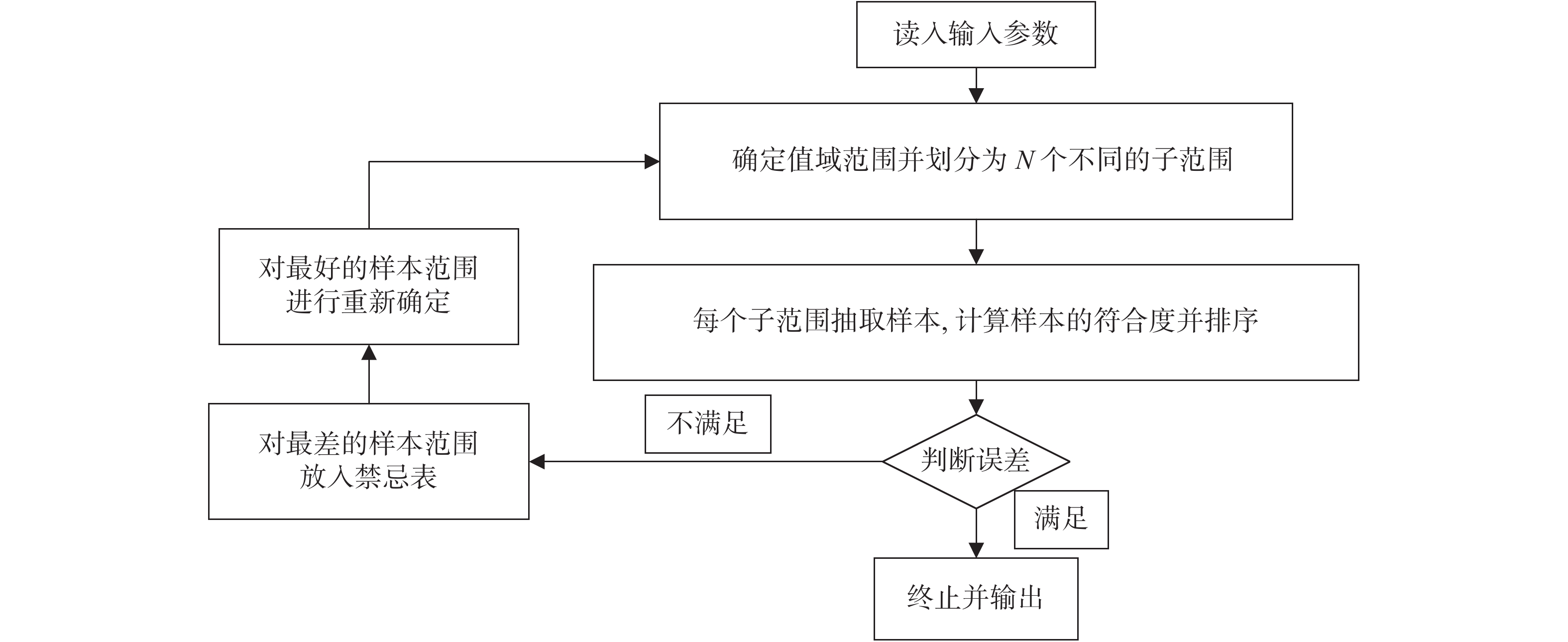
(2)禁忌搜索算法:该算法用禁忌表记录已到达过的局部最优点或过程,在下次搜索中利用禁忌表信息不再或有选择地搜索这些点或过程,以此跳出局部最优点。具体过程分5步:① 在解域范围均匀生成N个样本;② 计算每个样本的符合度并排序;③ 判断最高符合度的样本是否满足误差要求,若满足输出并退出搜索;④ 若不满足,将符合度低的样本及其领域放入禁忌表,在符合度高的样本附近重新搜索新样本;⑤ 回到step2。流程见图2。
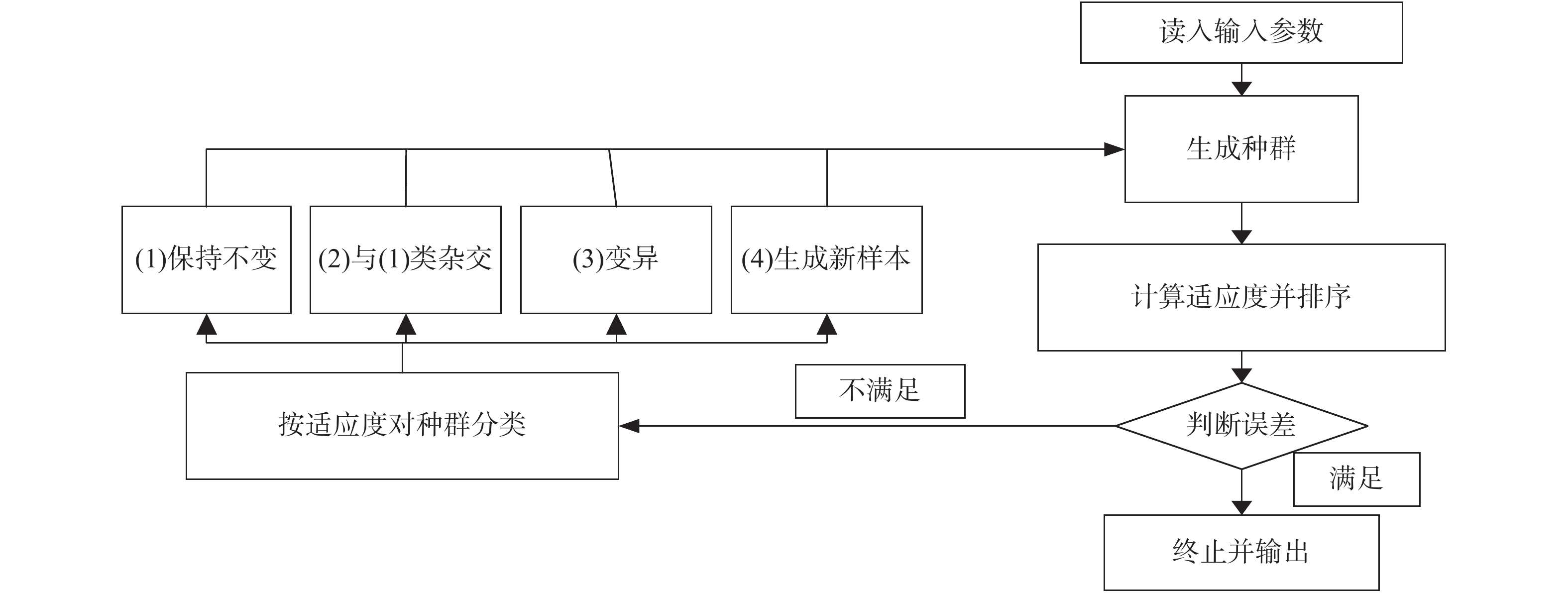
(3)遗传算法:该算法主要借用生物进化中“适者生存”规律,通过对“解”进行编码,遗传过程中通过杂交变异不断产生新的解,最终获得最优解。具体分5步计算:① 在解域范围生成初始种群;② 计算每个样本的适应度并排序;③ 若最高适应度的样本满足误差要求,输出并退出循环;④ 按照适应度从大到小将样本分成4类,第一类样本保持不变,但参与第二类的杂交;第二类样本与第一类样本杂交生成新样本;第三类变异生成新样本;第四类抛弃,并在第一类领域附近随机生成新样本;⑤ 将step4生成的样本组成新种群,回到step2。计算流程见图3。
|
图 2 禁忌搜索算法基本流程图 Figure 2 Basic flow chart of tabu search algorithm |
|
图 3 遗传算法基本流程图 Figure 3 Basic flow chart of genetic algorithm |
(4)蚁群优化算法:该算法是种分布式智能模拟算法,基本思想是模仿蚂蚁依赖信息素进行通信而显示出的社会行为。它是种基于总体优化、随机的通用试探法,可用于求解各种不同组合优化问题,具有通用性和鲁棒性。具体分5步计算:① 在解域范围生成初始蚁群;② 计算每个样本的信息素并排序;③ 如果最高信息素的样本满足误差要求,输出并退出循环;④ 按照信息素从大到小以一定概率向最高信息素附近移动(最高信息素的样本附件生成新样本);⑤ 将step4生成的样本组成新蚁群,回到step2。计算流程见图4。

|
图 4 蚁群优化算法基本流程图 Figure 4 Basic flow chart of ant colony optimization algorithm |
反演模型分析基于监测数据、高斯烟羽模型和不同优化算法相结合的方法,通过优化算法比较和实际案例验证的方法进行反演模型分析,研究使用的条件和参数见下文。
(1)优化算法的比较:采用几种优化算法进行源项反演计算,并比对不同算法的计算结果,选出较适用于源项反演分析的优化方法。目前优化算法主要是解决线性方程的求解(式3),本文针对前者反演求解式对不同算法进行了测试比较。
| $C = {C_0} + {\sum {{ X}O{Q_i} \cdot Q} _i}\;\;D = {D_0} + \sum {DX{Q_i} \cdot {Q_i}} $ | (3) |
式中,C为空气中浓度,Bq/m3;C0为本底或其他因素造成的浓度,Bq/m3;XOQi为弥散因子,s/m3;D为外照射剂量率,nGy/h;D0为本底或其他因素造成的剂量率,nGy/h;DXQi为剂量计算因子;Qi为源项释放率,Bq/s。
模拟数据基于高斯烟羽模型计算结果并符合随机误差生成,模拟输入数据见表1,其中C0 = 63.5,Q = 0.035,求解范围[0,800]。
|
|
表 1 模拟输入参数 Table 1 Analog input parameters |
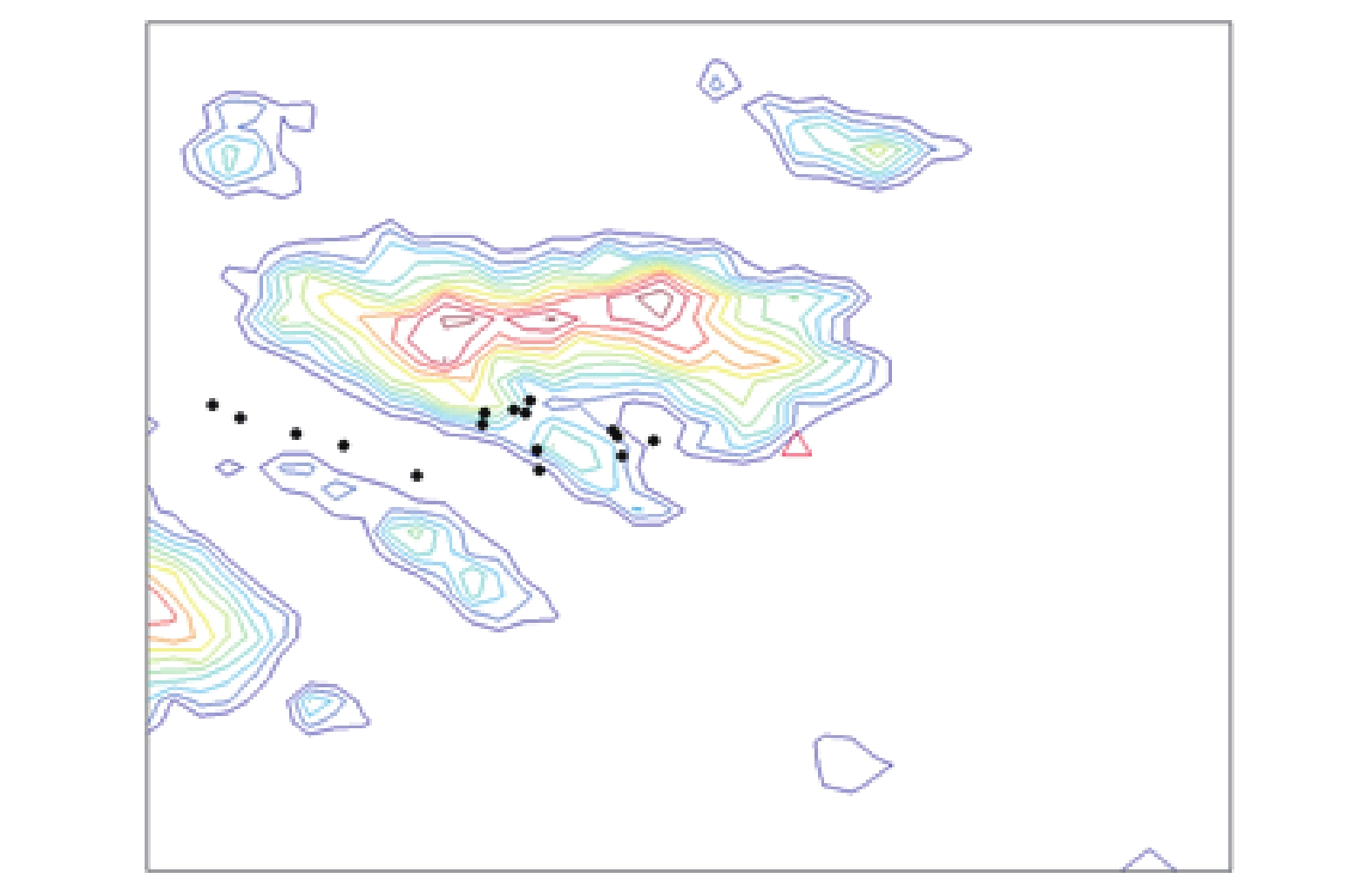
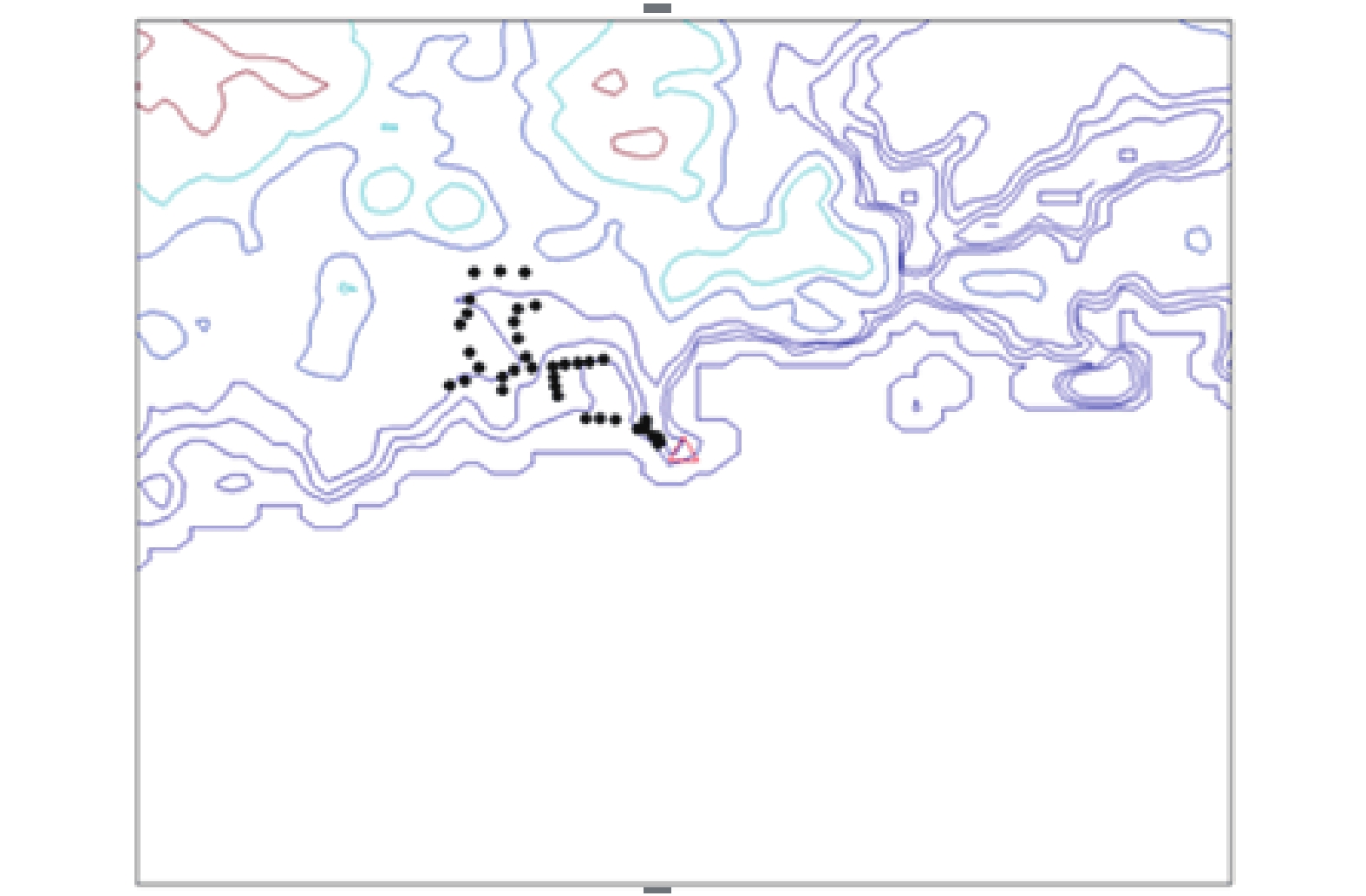
(2)实际案例的验证:选用复杂和简单地形下的实际扩散示踪案例对优化模型计算准确性进行了验证。现场试验地形见图5、图6 (复杂和简单地形实验释放时长分别为45 min和1 h,每次试验采样点连续采样3次(时长10 min,间隔5 min),各采样点从采样开始到结束共计40 min。采样结果为采样点10 min的平均结果,总反演时长为释放时长。)源项、气象和监测点数据分别见表2、表3、图7、图8、图9、图10。
|
图 5 SF6现场试验复杂地形及采样点分布 Figure 5 Complex terrain and sampling point distribution of SF6 field test |
|
|
表 2 源项数据 Table 2 Source term data |
|
|
表 3 复杂地形反演使用的气象数据 Table 3 Meteorological data in complex terrain for inversion |
|
图 6 SF6现场试验简单地形及采样点分布 Figure 6 Flat terrain and sampling point distribution of SF6 field test |
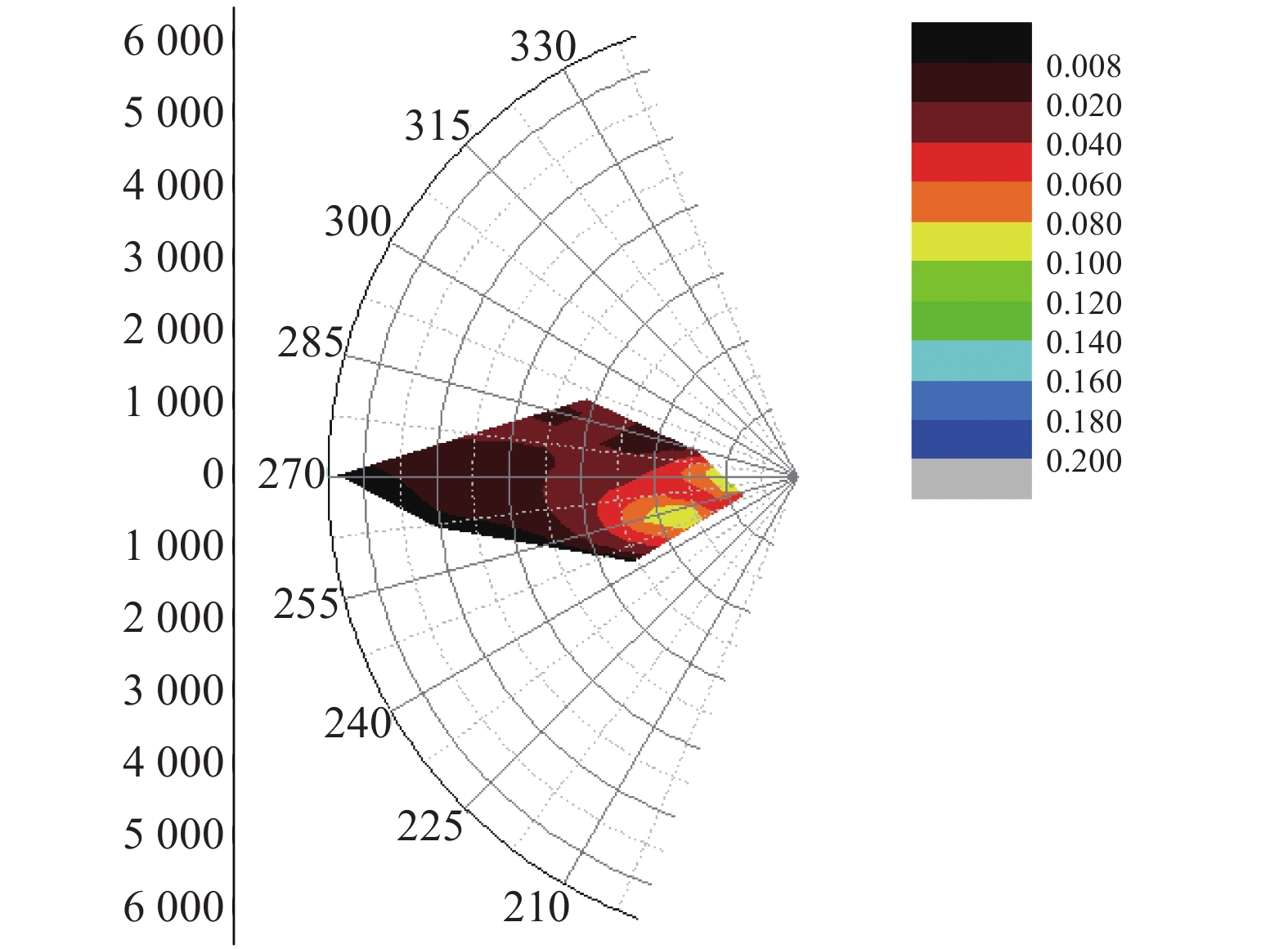
|
图 7 复杂地形条件的监测数据分布图 Figure 7 Distribution of monitoring data in complex terrain conditions |
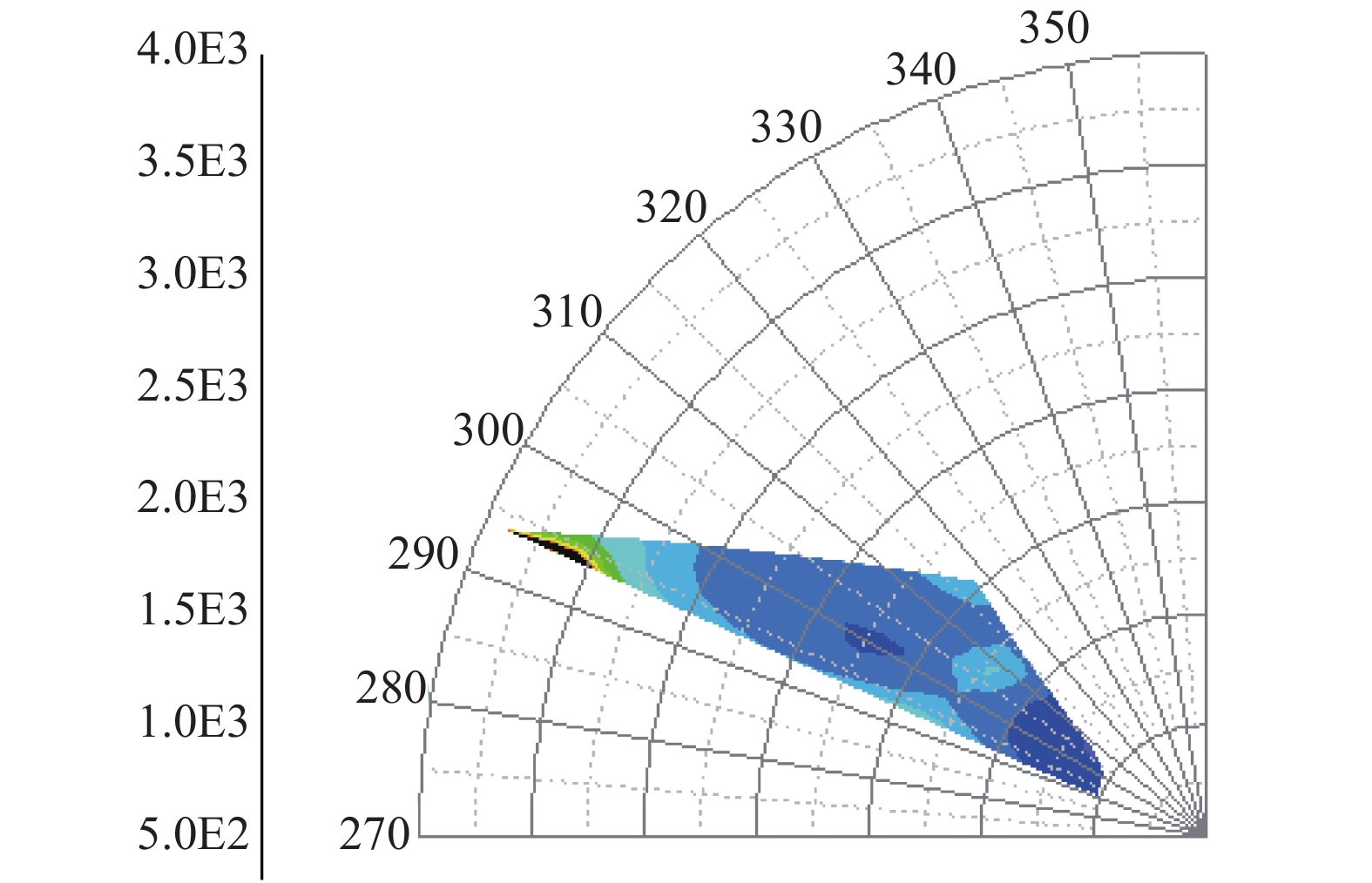
|
图 8 简单地形条件的环境监测数据分布图(采样时间12:30~12:40) Figure 8 Distribution of environmental monitoring data under flat terrain conditions |
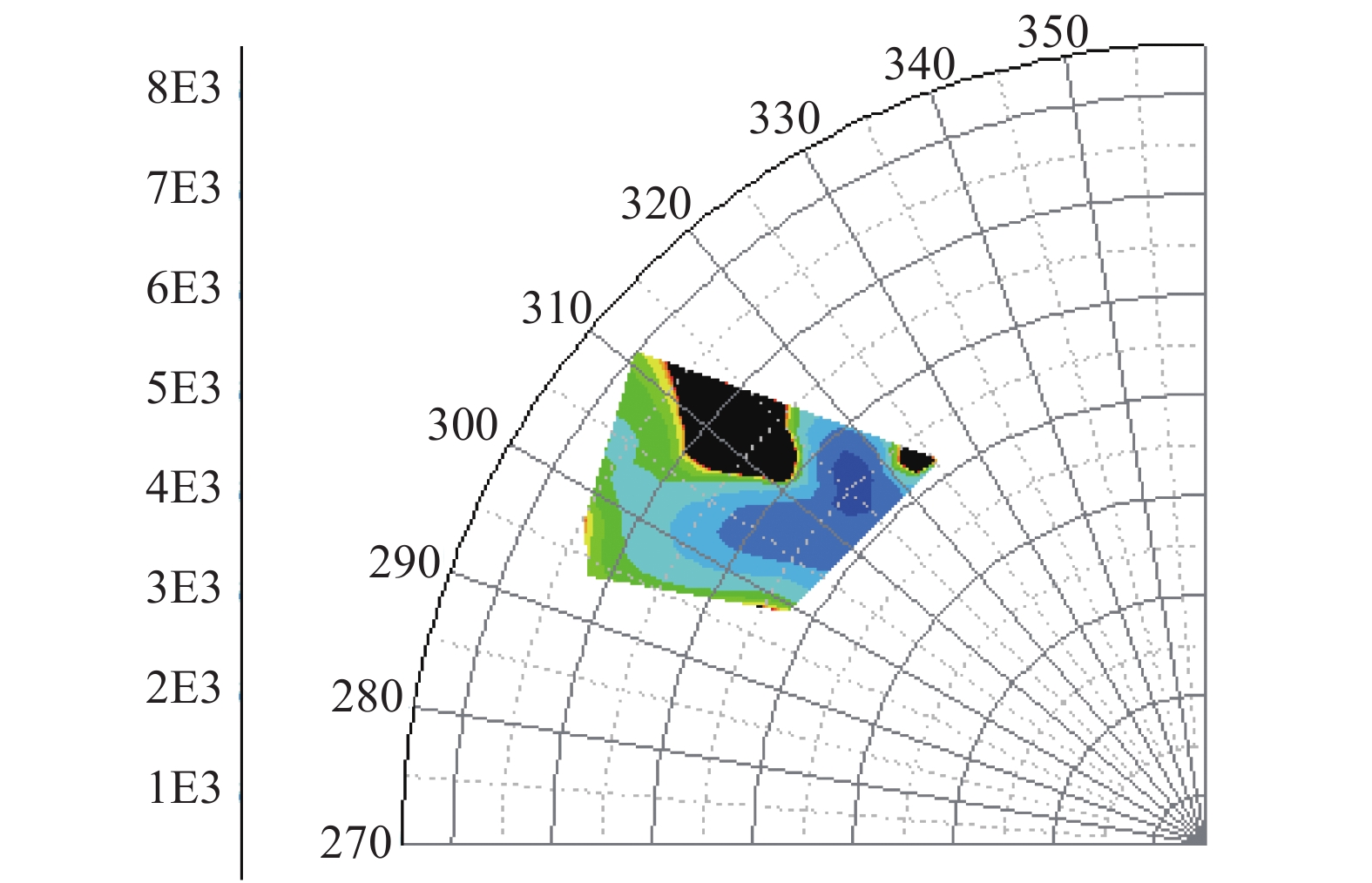
|
图 9 简单地形条件的环境监测数据分布图(采样时间12:40~12:50) Figure 9 Distribution of environmental monitoring data under flat terrain conditions |
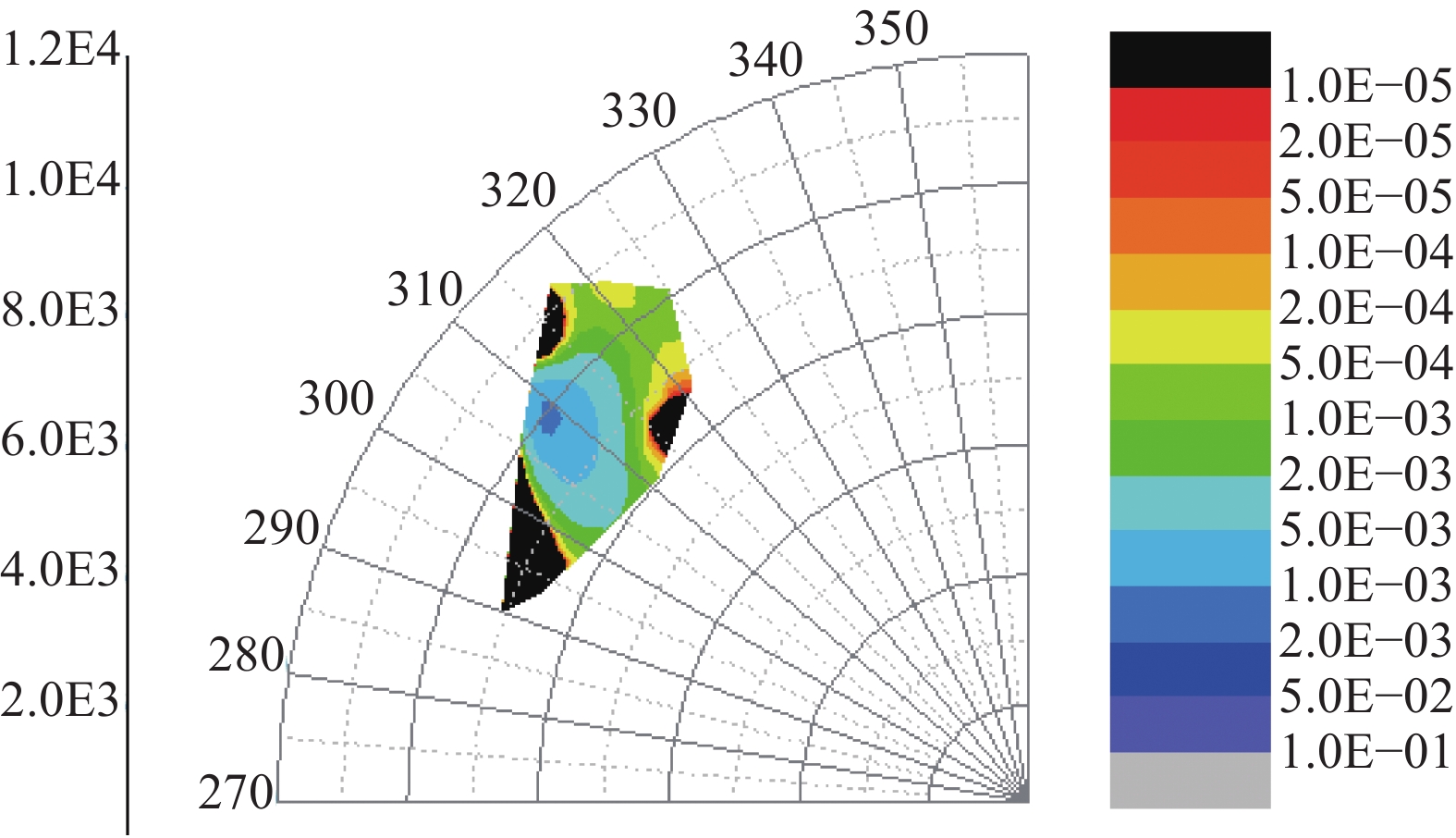
|
图 10 简单地形条件的环境监测数据分布图(采样时间12:50~13:00) Figure 10 Distribution of environmental monitoring data under flat terrain conditions |
基于第1章节中的理论分析和参数,用于比较优化算法的结果见表4。
|
|
表 4 简单地形反演中的气象数据 Table 4 Meteorological data in simple terrain for inversion |
基于第1章节中的理论分析和参数,实际案例的验证结果见表5。
|
|
表 5 模拟结果 Table 5 Simulation results |
从表5可看出:①最小二乘法效率最高,仅需一次解析计算即可得到结果;②禁忌搜索算法、遗传算法、蚁群算法计算迭代次数与给定的解范围和搜索样本数有关,当给定解范围越精确、搜索样本越多,需要迭代次数越少;但给定搜索样本越多,每步计算量也随之增大,总计算效率不会提高很多;③对于多元一次方程形式(线性)的反演模型,最小二乘法是最有效的方法;对于多元非线性方程形式的反演模型来说,则需要做更多的研究比较。因此对于多元一次方程形式(线性)的反演模型,推荐选用最小二乘法。
3.2 实际案例分析表6计算结果显示:①采用反演模型进行释放源项的反演计算是可行的,其误差精度满足后果评价要求;② 采用文中直线高斯烟羽模型的源项反演计算,对于简单地形下的反演结果为实测值的0.92倍,精度较高;对于复杂地形条件下的反演结果为实测值1.5倍,受模型本身限制,误差相对较大。
|
|
表 6 实际释放量与计算结果的比较 Table 6 Comparison of actual release and calculation results |
通过本文的研究,得出以下主要结论:
(1)对于直线高斯烟羽模型,长期事故释放情景只能采用分段处理方式,进而获取整个释放期间的释放量。因文中采用模型的限制,对于简单地形地区的反演效果较好,对于复杂地形条件,通过对监测点的选择可有效提高反演精度。
(2)从优化算法的对比来看,虽然各类优化算法均可实现释放量的反演分析,最小二乘法效率最高。对于其他算法,变量较少时容易实现计算,当待求解变量数很多时,对于程序的编制,以及计算效率有很高的要求。
(3)因模型的限制,对于复杂地形条件和复杂气象条件时的反演存在较大的困难,因此需要后续研究考虑更精确的扩散模型。
| [1] |
徐志新, 奚树人, 曲静原. 核事故源项反演技术及其研究现状[J]. 科技导报, 2007, 25(5): 16-20. Xu ZX, Xi SR, Qu JY. Review on source inversion technology in analyzing nuclear accidents[J]. Sci Technol Rev, 2007, 25(5): 16-20. DOI:10.3321/j.issn:1000-7857.2007.05.004 |
| [2] |
宁莎莎, 蒯琳萍. 混合遗传算法在核事故源项反演中的应用[J]. 原子能科学技术, 2012, 46(zl): 469-472. Ning SS, Kuai LP. Back-calculation of source terms by hybrid genetic algorithm in nuclear power plant accident[J]. At Energy Sci Technol, 2012, 46(zl): 469-472. DOI:1000-6931(2012)SO-0469-04 |
| [3] |
侯闻宇, 凌永生, 赵丹, 等. GA-BP算法应用于核事故源项反演的研究[J]. 安全与环境学报, 2016, 16(6): 24-28. Hou WY, Ling YS, Zhao D, et al. GA -BP neural network algorithm and its application to the nuclear accident source term inversion[J]. J Saf Environ, 2016, 16(6): 24-28. DOI:CNKI:SUN:AQHJ.0.2016-06-007 |
| [4] |
余胜威. MATLAB优化算法案例分析与应用[M]. 北京:清华大学出版社, 2014. Yu SW. Case analysis and application of MATLAB optimization algorithm[M]. Beijing:Tsinghua University Press, 2014. |
| [5] |
Steven G. Homann. HotSpot-Health Physics Codes Version 2.07 User's Guide[M]. March 1, 2009.
|




