高浓缩钚作为核武器重要组成材料，主要含有²³⁹Pu、²⁴⁰Pu、²⁴¹Pu和²⁴¹Am等放射性核素^[1]，可造成内照射和外照射危害。通常来讲，在核武器试验或发生核武器核事故时，主要放射性危害来自裂变核素，而且主要是α发射体形成的内照射。一般认为，在核试验或核武器事故中，不存在导致严重健康危害问题的大量β和(或)γ发射体^[2]。但在正常情况下，由于外层材料的密封和屏蔽作用，电离能力较强的α射线、β射线基本不会从内层泄漏出来，因而，内照射的危害是比较小的，而穿透能力较强的X射线、γ射线和中子射线可穿透钚材料本身和外层屏蔽材料，从而对操作人员造成外照射危害，由于接触距离近、时间长，其辐射危害应引起重视。

由于高浓缩钚发射的X射线、γ射线射线能量偏低，对一般的辐射监测仪器响应能力提出了更高的要求，且在有些情况下无法监测(如在可行性论证阶段)，无法开展工作人员辐射安全评估，这时就需要对武器钚的贯穿辐射场进行理论计算。若要保证计算的准确性和科学性，必须要考虑高浓缩钚所含放射性核素的多样性、能量线的复杂性，此时，对于操作高浓缩钚的工作人员来说，由于距离源较近，采用简单的点源衰减模式是不合适的，所以，应考虑另外的计算方法予以解决。

本文通过对高浓缩钚辐射特性的分析，研究了其贯穿辐射场的形成机理，提出基于宽束理论的γ辐射场计算模型、基于分出截面法的中子辐射场计算模型^[3]，为贯穿辐射场计算提供解决方案。

1 辐射场计算方法 1.1 辐射场形成机理分析

高浓缩钚材料中主要含有²³⁹Pu及少量²⁴⁰Pu、²⁴¹Pu和²⁴¹Am，可发射α、β、X、γ射线。此外，²³⁹Pu和²⁴⁰Pu为超铀元素，可产生自发裂变中子。²⁴¹Am和杂质发生(α，n)反应产生中子，钚发射的γ射线以及自发裂变中子、增殖中子和(α，n)反应产生的中子会对工作人员形成外照射伤害。各核素主要辐射特性见表 1。

1.1.1 高浓缩钚γ辐射特性分析

钚同位素的γ谱构成比较复杂，如²³⁹Pu在能量几十keV~800 keV之间有众多的γ射线，并且有很多γ射线的能量相近，在γ谱形成重峰，不易分辨。此外，不同纯度的钚材料在不同能段的γ峰强度有差异，特别是²⁴¹Am的浓度影响较大。图 1是高纯度²³⁹Pu(6% ²⁴⁰Pu)的γ能谱。钚的同位素²³⁹Pu、²⁴⁰Pu、²⁴¹Pu和²⁴¹Am在率变过程中都发射各自的特征γ射线，其主要γ射线的能量和强度如表 2所示。

1.1.2 高浓缩钚中子辐射特性分析

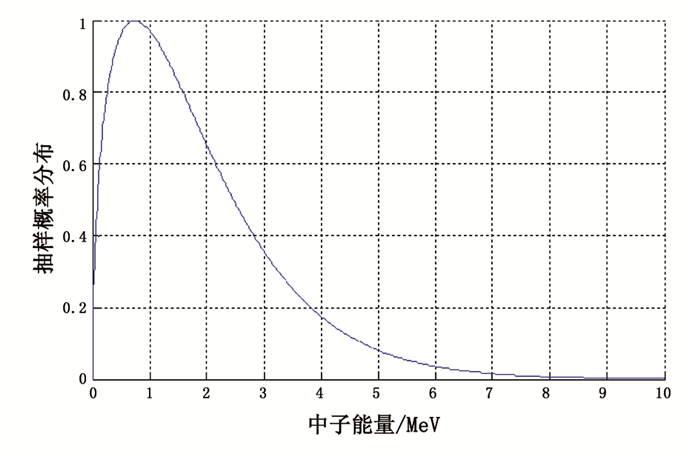
钚材料的中子主要由自发裂变中子和(α，n)反应中子两部分组成。大多数情况下，当材料中含有一定量较高α衰变率的²⁴¹Am核素时，(α，n)产生的中子占钚材料中释放中子的主要部分，两者产生的中子能谱见图 2和图 3，钚主要同位素自发裂变中子产额见表 3，表 4列出了部分钚同位素的(α，n)中子释放率。

1.2 辐射场计算方法 1.2.1 高浓缩钚γ辐射场计算

通过对高浓缩钚中含有的放射性核素特性、射线特性和结构材料的分析，可通过基于宽束减弱规律计算高浓缩钚材料外γ射线空气吸收剂量率。高浓缩钚材料介质可视为无限均匀，外面的结构或封装材料简单且有一定厚度，此种情况下，从钚材料中发射出来的γ射线经二次或多次散射后仍有可能穿出结构材料，所以，基于宽束减弱规律，可建立其γ射线空气吸收剂量率计算公式：

${\dot D_\mathit{i}} = {\mathit{\dot D}_{\mathit{i}{\rm{0}}}}B{e^{ - \mu r}} $

${\dot D_\mathit{i}} = \sum\limits_{i = 1}^n {{{\mathit{\dot D}}_{\mathit{i\varepsilon }}}} $式中：$\dot D$为经过屏蔽层之后的γ吸收剂量率，单位为Gy/h；${\dot D_\mathit{i}}$为经过屏蔽层之后核素i产生的γ吸收剂量率，单位为Gy/h；${\dot D_{\mathit{i}{\rm{0}}}}$为未经过屏蔽层之前核素i产生的γ吸收剂量率，单位为Gy/h；B为该条件下的累积因子，无量纲。其可通过伯杰公式计算得出，计算公式为B=1+αμRe^-bμR，a和b可通过查表得到；μ为屏蔽物质的衰减系数，单位为cm^-1。它是基于宽束减弱规律计算的关键参数，可通过查表、查图获取；r为屏蔽层的厚度，单位为cm；n为钚材料中所含放射性核素的个数；ε为放射性核素i中某一能量线的分支比。

需要说明的是，${\dot D_{\mathit{i}{\rm{0}}}}$可根据高浓缩钚材料加工形状确定是否为点源、线状源、圆盘源、球面源、圆柱面源、球体源或无限大体积源，然后通过比释动能率计算公式得到^[5]。对于点源来说，可先计算出比释动能率，然后转化成空气吸收剂量率。其计算公式为${\dot K_\mathit{i}} = \frac{{A \cdot \mathit{\Gamma k}}}{{{R^{\rm{2}}}}}$, A为源的活度(单位为Bq)，R为离源距离(单位为m)，Γk为比释动能率(单位为Gy·m²·Bq^-1·s^-1)。

1.2.2 高浓缩钚中子辐射场计算

高浓缩钚材料中发射的中子为快中子，快中子通过屏蔽物质时，主要发生弹性与非弹性散射而损失能量，此外，被物质吸收时，还要发射俘获γ射线。它与原子核的作用过程，以及截面与能量的关系都相当复杂。所以，计算中子在屏蔽体中的减弱规律，远比γ射线复杂，所以，大多数情况下，采用简单的近似或经验公式计算，如查图法和半厚度法^[6]。但在需要精确计算时，采用上述方法是不够的，而要考虑基于分出截面法的计算方法。

分出截面法的原理是中子通过单位厚度材料时，从高于某能量阈的中子群中分出来而进入较低能量的中子群中支的几率。经分析，高浓缩钚发射的快中子在外层屏蔽体中各向同性，满足指数衰减规律，基于分出截面理论，建立了高浓缩钚中子剂量当量率计算公式：

$\dot H = \frac{S}{{4{\rm{ \mathit{ π} }}{\mathit{R}^{\rm{2}}}}}{d_\mathit{H}}{B_\mathit{n}}{e^{ - \sum {_{{R^r}}} }}{\rm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;3)}} $

3)

式中：$\dot H$为剂量当量率，单位为Sv/s；S为中子源强，即源活度与中子产额的乘积，单位为s^-1；d_H为中子剂量当量换算因子，单位为Sv·m²；r是屏蔽层厚度，单位为m；R是距源的距离，单位为m；B_n是中子积累因子，无量纲；Σ_R是含氢材料的宏观分出截面，单位为m^-1。

1.2.3 计算方法验证

为验证计算方法的准确性，结合某次高浓缩钚材料操作实际，依据本文提出的贯穿辐射场计算方法，对高浓缩钚材料周围贯穿辐射水平进行了计算，并对照实际监测结果进行比对。

2 结果

从图 4和表 5中可以看出：

① 计算的中子、γ剂量率与实际测量吻合情况较好，相对测量值而言，大部分中子计算值偏大而γ计算值偏小。分析原因主要是：中子测量时，受探测器能量响应范围的限制，测量值相对偏小，而γ射线测量时，探测器受中子影响导致测量结果比计算值偏大。②随着距表面距离的增加，中子、γ计算值与测量值的相对误差呈减小趋势。分析主要原因为距离表面较近时，从侧面进入计数栅元的粒子比重较大，而这部分粒子在实际测量过程受晶体形状、尺寸及外壳包装屏蔽等影响，导致探测效率小于从正面入射的粒子，距离远时，该部分粒子比重减小，致使实际测量与理论计算误差变小。③进一步分析，中子对γ射线测量影响较大。另外，材料中²⁴¹Am的含量对γ剂量率的影响较大，尤其以59.54 keV特征射线影响最为显著。

3 讨论

本文针对高浓缩钚材料辐射场计算的实际，提出了基于宽束理论的γ辐射场计算模型和基于分出截面法的中子辐射场计算模型，通过原理分析和实测验证，证明本文提出的计算方法是合理可行的，能够满足科学性和准确性要求。通过进一步分析，高浓缩钚材料外辐射场计算本质上是γ和中子在屏蔽体中的减弱计算。本文研究提出的γ、中子辐射场计算方法有充足的理论依据，且计算过程相对比较简单，并有一定的精确度保证。但任何一种计算方法都有一定的局限性，例如，在利用本文提出的方法进行多层屏蔽γ辐射场计算时，因衰减系数难以确定，因此适用性较差。同样，对于利用本文提出的基于分层截面法进行中子辐射场计算时，屏蔽层中要含有足够的氢和重核材料，应用本方法时需要作一定的假设和近似，会造成误差变大。因此，在计算方法选择时，应对计算对象、条件和边界等进行全面深入的分析，避免模型和方法选择的问题而导致误差不可接受。