近些年来,中子谱测量技术研究一直伴随着中子探测技术的发展而不断完善,被广泛应用于辐射防护、核物理、核技术、核聚变等离子体诊断及放射治疗等领域[1]。随着现代技术的发展,中子谱仪的性能较其早期已有了巨大改善,然而由于辐射防护涉及的中子场具有能量范围宽、方向分布不确定、伴随其它射线干扰等复杂特性,且不同环境的中子能谱分布千差万别,因而设计一种能量分辨率好,且具有理想能量和角响应的中子谱仪十分困难。
多球中子谱仪,又称Bonner球中子谱仪,由Bramblett等[2]于1960年首次将其用于中子能谱测量,然后针对不同的研究目标得到多种形式的发展。多球中子谱仪由于具有能量覆盖范围广、灵敏度高、响应几乎各向同性、操作简单、对电子学噪声及光子甄别能力较好等优点,至今仍被广泛使用,特别是在中子谱学和辐射防护剂量学中[3]。但由于受限于响应函数的重叠,多球谱仪在低能及中能区的能量分辨率相对较差,导致其在某些领域的使用受到较大程度的限制。
为了提高多球谱仪的能量分辨率,针对不同研究对象和中子能量范围,人们对其进行了针对性的改进。在硼中子俘获疗法治疗癌症领域,Wang和Blue[4]研制了一种与多球谱仪类似的中子谱仪,该谱仪包含一个球形3He正比计数器和一套由半球状10B球壳包围的石蜡球,可改善1 eV~10 keV能区的分辨率。该改进是通过改变吸收材料厚度在低能和中能区形成不同的响应函数峰,进而达到提高相应能区分辨率的目的,但由于存在测量能量范围有限、响应各向异性等不足,使其不能满足某些辐射防护场所的需要。为改善对医院中子照射器中子束超热能区的分辨率,陈军等[5]建立了一套改进的主动式多球谱仪,包含一个SP9型球形3He正比计数器,九个常规聚乙烯单元,以及四个覆盖硼壳的扩展单元。该方法可较明显改善常规谱仪在100 eV~100 keV能区的能量分辨。此外,Ueda等[6]利用10B含量0.14%的硼酸水溶液做慢化体,也可较明显的改善多球谱仪在超热中子能区的分辨率。
基于上述研究,本工作采用中心置有3He正比计数器的聚乙烯内球外覆盖不同掺碳化硼聚乙烯球壳的形式,引入切阈的方法进一步对多球谱仪在中低能区的能量分辨加以改善,以便为现场剂量测量仪表校准提供依据。
1 原理及方法出于防护的目的,需要对工作场所辐射场中子能谱进行测量,由于这些辐射场具有较宽的能量范围[7-9],要求谱仪对中子能谱的测量范围尽可能宽广。多球中子谱仪作为目前唯一可覆盖热能区至GeV能区的谱仪,其基本原理是不同能量的中子在不同尺寸的慢化球内被慢化的程度不同,到达慢化球中心后引起的响应也不同,从而可以反映所测辐射场中子的能量分布情况。从数学角度分析,其能谱测量关系为:
| $ {N_k}\left( \mathit{\Phi } \right) = \int {_{{E_{\mathit{min}}}}^{{E_{\mathit{max}}}}{R_k}\left( E \right)\mathit{\Phi dE}} $ | 1) |
其中Nk为第k个探测器的中子计数,Rk(E)为第k个探测器对中子的响应函数,Φ(E)为待测中子能谱,Emin和Emax是待测中子的最低和最高能量。理论上,得到响应函数后,通过解谱即可得到中子能谱。阈探测器由一系列具有不同中子反应阈能的探测器组成,其基本原理是利用具有不同反应阈能的探测器对不同能量中子的响应不同来获得中子能谱[10]。该探测器在阈值以下无响应,计数只反应能量高于阈值的中子能谱信息,由此可以准确去除阈值以下中子的干扰,如在多球中子谱仪中采用此能谱测量原理,将提高解谱精度,改善谱仪的能量分辨率。
因此,本工作借鉴阈探测器测量中子能谱的思路,结合两种谱仪的优点,在纯聚乙烯内球外覆盖一套含硼聚乙烯球壳,通过调整含硼聚乙烯厚度和硼含量改变慢化体对中子的慢化和吸收性能,降低对低能中子的响应从而形成不同的响应阈值。该方法可明显提高1 eV~10 MeV能区的能量分辨率,特别是超热中子能区和注量-剂量当量转换系数随中子能量变化剧烈的能区。
2 响应矩阵计算 2.1 慢化体设计谱仪的设计基于对注量能量响应的计算,为选择合适方案,需综合考虑能量分辨率、灵敏度、加工成本、体积重量等各方面因素。为覆盖较宽的能谱测量范围,同时具有较高的能量响应,选取在宽能量范围内具有相对较高且平缓能量响应的直径为11 cm的聚乙烯作慢化体内球;为在镉切割能以上能区形成不同的响应阈值,选择掺有70%碳化硼的聚乙烯球壳作外层中子慢化吸收材料,但鉴于球壳厚度较大时低含量含硼聚乙烯具有相近甚至更好的切阈能力,且重量更轻,因此部分球壳选择掺有20%碳化硼的聚乙烯。
2.2 计算模型本工作采用英国Centronic公司生产的SP9型球形3He正比计数器,内充200 kPa的3He气体和120 kPa的氪气(氪气用以减小壁效应)。谱仪系统包含1个裸的、1个裸的包1 mmCd以及12个含慢化体的探测器,慢化体内层中子慢化材料为直径11 cm、密度0.91 g/cm3的纯聚乙烯,外层中子慢化吸收材料为碳化硼含量分别为70%(厚度分别为0.5、1.0、1.5、2.5、3.5、4.5、5.5、6.5、7.5、8.5 cm,密度1.65 g/cm3)和20%(厚度分别为9.0、10.0 cm,密度1.04 g/cm3)的含硼聚乙烯球壳。计算时使用3He原子数密度为4.95×1019 cm-3,不锈钢球壳(含Cr:19.5%、Fe:70.5%、Ni:10%)内外半径分别为1.60 cm和1.65 cm。平行中子束入射到慢化体球上(如图 1),假设各结构之间无空隙,设计时不考虑线缆等对计算的影响。

|
图 1 多球谱仪的响应函数计算模型 |
为方便比较,利用三维粒子输运程序MCNP[11]分别计算常规多球谱仪(谱仪系统包含1个裸的、1个裸的包1 mmCd以及10个聚乙烯直径范围从2.5英寸~12英寸的慢化体探测器)和改进的多球谱仪在中子能量10-9~20 MeV范围的能量响应函数,该程序曾用于以6LiI为中心探测器的多球谱仪对响应函数的计算[12]。计算中,采用“俄罗斯轮盘赌”方差减小技术以提高计算效率,计算结果如图 2和图 3所示。

|
图 2 计算的常规多球谱仪的中子响应函数 |

|
图 3 计算的11 cm聚乙烯球外覆盖不同含量及厚度含硼聚乙烯球壳的中子响应函数 |
从图 2可知,对常规多球中子谱仪,一组不同厚度的慢化体可获得一组独立的响应曲线。随着慢化体厚度的增加,测量中子的能量越高,响应函数峰位逐渐向高能区转移。在低能区和快中子能区,其响应函数曲线均存在明显的峰,而在阈切割能以上的超热中子能区,由于响应函数存在较大程度的重叠而无明显的峰。由图 3可知,除裸探测器和包镉的裸探测器外,一组不同厚度和硼含量的慢化体对应一组有阈的响应曲线。随着含硼聚乙烯厚度和硼含量的增加,探测器对低能中子的响应明显降低,形成了一系列响应阈值,其形状与阈探测器谱仪的响应函数曲线相似。
比较两种多球谱仪的响应函数曲线(图中凹陷处源于Cd壳和11B的共振吸收),可以定性的估计其在镉切割能附近以及100 keV~20 MeV均具有最佳的能量分辨率。而在能量介于10 eV~100 keV之间的能区,由于常规多球谱仪的响应函数存在相当大程度的重叠,其能量分辨率相对较差;对改进后的多球谱仪,由于不同慢化体在该能区具有不同的响应阈值,相较常规多球谱仪而言其能量分辨率应有明显的改善。但从定量的角度,很难对两种谱仪在不同能量范围的能量分辨率给出准确的判断。
3 谱仪分辨能力计算结果与分析 3.1 多球中子谱仪分辨能力评价方法介绍为解决地球物理勘探中计算数据结果分辨率低的问题,Backus和Gilbert[13-14]引入了地球物理反演问题情况下分辨能力的求解方法,Reginatto[15]将该方法用于对高能多球中子谱仪能量分辨率的评价。按照Reginatto的方法,考虑Φ(E)在点E0的线性平均为如下形式
| $ {\left\langle \mathit{\Phi } \right\rangle _{{E_0}}} = \int {A\left( {{E_0}, E} \right)\mathit{\Phi }\left( E \right)dE} $ | 2) |
其中,平均核A是能量E的函数。为构造平均核,将其表示为响应函数的线性方程
| $ A\left( {{E_0}, E} \right) = \sum\limits_{k = 1}^n {{a_k}\left( {{E_0}} \right){R_k}\left( E \right)} $ | 3) |
其中,ak(E0)是常数,n是探测器的数目。不难看出,不用解谱,根据测量结果平均核A可直接提供 < Φ>E0的近似估计。利用(1)~(3)式,该近似估计可写为如下形式
| $ {\left\langle \mathit{\Phi } \right\rangle _{{E_0}}} = \sum\limits_{k = 1}^n {{a_k}\left( {{E_0}} \right){N_k}} $ | 4) |
随后通过优化选择ak(E0)值以使平均核A(E0, E)近似为δ函数。为了用平均核量化能量分辨率,引入以下两个参数:
| $ {L_{AV}}\left( {{E_0}} \right) = \int {A\left( {{E_0}, E} \right)E\;dE} $ | 5) |
| $ {\left[{\Delta L\left( {{E_0}} \right)} \right]^2} = \int {A\left( {{E_0}, E} \right){{\left( {E -{L_{AV}}\left( {{E_0}} \right)} \right)}^2}dE} $ | 6) |
LAV提供了平均核A(E0, E)以E0为中心的集中程度,△L则是对平均核宽度的一个量化,反应了在能量E0时分辨能力的好坏。如果平均核近似于δ函数,即A(E0, E)→δ(E0, E),则相应参数则写为LAV(E0)→E0和△L(E0)→0,即此时具有最佳的能量分辨。
3.2 计算结果与分析为比较两种谱仪对中子能谱的分辨能力,利用上述方法对常规多球谱仪和改进后的多球谱仪在不同能量的平均核分布进行了计算,结果如图 4和图 5所示。
|
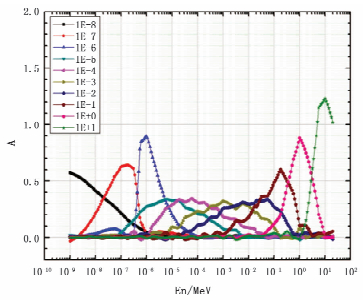
图 4 常规多球谱仪在不同能量的平均核A(E0, E) |
|
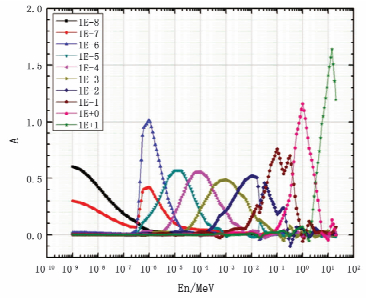
图 5 改进型多球谱仪在不同能量的平均核A(E0, E) |
由常规多球谱仪的平均核分布曲线可以看出,随着中子能量的变化,其在E0=10-6,10+0和10+1MeV时平均核宽度较窄因而具有较好的能量分辨率,而在其它能量时较差。由改进后多球谱仪的平均核随中子能量变化的分布曲线可知,其在E0=10-5~10-1MeV时平均核宽度明显变窄,因此能量分辨率显著提高,同时在常规多球谱仪能量分辨较好的E0=10-6,10+0和10+1MeV能量附近也略有改善。
为了定量的评价多球中子谱仪分辨能力的改善程度,使用平均核参数LAV和△L对两种谱仪在不同能量范围的分辨能力进行了比较,对比如表 1所示。
|
|
表 1 平均核参数 |
比较两套多球中子谱仪平均核参数可以看出,改进后的多球中子谱仪在1 eV~10 MeV能量范围内的平均核宽度△L明显变窄,尤其是在常规多球谱仪能量分辨率较差的10 eV~100 keV能区(100 eV能量附近可提高约35.6%),该结果与上文对谱仪能量分辨率的定性评估相吻合。而平均核宽度作为分辨能力的量度,也反应了谱仪对中子能谱在不同能区的能量分辨率。由此可见,利用掺硼慢化体切阈的方法可在很大程度上提高多球中子谱仪在低能和中能区的能量分辨率。
4 结果及讨论本文利用MCNP程序模拟计算了常规多球谱仪与使用掺硼聚乙烯作中子慢化和吸收材料的改进多球谱仪在10-9~20 MeV能量中子的响应函数,基于独立于解谱过程的一种分析多球中子谱仪数据的方法,通过比较平均核参数及其分布结果发现,改进后的多球中子谱仪在1 eV~10 MeV能量范围内的分辨能力较常规多球谱仪有很大程度的提高。该能区既涵括了超热中子能区,也涵括了辐射防护关注的注量-剂量当量转换系数随中子能量变化剧烈的能区,因此,利用基于掺硼慢化体的多球中子谱仪开展辐射场中子能谱测量,可在低能和中能区获得更准确的中子能谱,为现场剂量测量仪表校准提供可靠依据。
本设计工作仅对基于切阈原理提高能量分辨率的方法作简单介绍,以论证方法的可行性。在实际研究工作中,针对不同的测量对象和要求,通过选用不同参数的中子探测元件,以及对慢化体尺寸或成分的进一步优化,可更为细致的调整谱仪关注能区的能谱测量精度。
| [1] |
Brooks F D, Klein H. Neutron spectrometry-historical review and present status[J]. Nucl Instr and Meth, 2002, A 476: 1-11. |
| [2] |
Bramblett R L, Ewing R I, Bonner T W. A New Type of Neutron Spectrometer[J]. Nucl Instr and Meth, 1960, 9: 1-12. DOI:10.1016/0029-554X(60)90043-4 |
| [3] |
Alevra A V, Thomas D J. Neutron spectrometry in mixed fields:multisphere spectrometers[J]. Radiat Prot Dosim, 2003, 107: 37-72. DOI:10.1093/oxfordjournals.rpd.a006388 |
| [4] |
Wang C K, Blue T E. A neutron spectrometry for neutrons with energies between 1 eV and 10 keV[J]. Nucl Instr and Meth, 1990, A 290: 237-241. |
| [5] |
陈军, 李春娟, 李玮, 等. 多球谱仪测量BNCT医院中子照射器中子束能谱[J]. 原子能科学技术, 2014, 48(11): 2127-2132. DOI:10.7538/yzk.2014.48.11.2127 |
| [6] |
Ueda H, Tanaka H, Sakurai Y. Reprint of the improvement of the energy resolution in epi-thermal neutron region of Bonner sphere using boric acid water solution moderator[J]. Appl Radiat Isot, 2015, 106: 107-110. DOI:10.1016/j.apradiso.2015.10.010 |
| [7] |
ISO. Reference Neutron Radiations-Characteristics and Methods of Production of Simulated Workplace Neutron Fields, ISO 12789[J].2000.
|
| [8] |
Griffith RV, Palfalvi J, Madhvanath U. IAEA Tech. Rep. 318[R]. 1990.
|
| [9] |
Griffith RV, Palfalvi J, Siebert B R L. IAEA Tech. Rep. 403[R]. 2001.
|
| [10] |
Apfel R E, d'Errico F. A neutron spectrometer based on temperature variations in superheated drop compositions[J]. Nucl Instr and Meth, 2002, A476: 298-303. |
| [11] |
X-5 Monte Carlo Team. MCNP-A General Monte Carlo N-Particle Transport Code[R]. Los Alamos National Laboratory Report, LA-CP-03-0245, Version 5, US: 2003.
|
| [12] |
Mazrou H, Idiri Z, Sidahmed T, et al. MCNP5 evaluation of a response matrix of a Bonner Sphere Spectrometer with a high efficiency 6LiI (Eu) detector from 0.01 eV to 20 MeV neutrons[J]. Radioanal Nucl Chem, 2010, 284: 253-263. DOI:10.1007/s10967-010-0493-9 |
| [13] |
Backus G E, Gilbert J F. Numerical Applications of a Formalism for Geophysical Inverse Problems[J]. Geophys J R Astr Soc, 1967, 13: 247-276. DOI:10.1111/gji.1967.13.issue-1-3 |
| [14] |
Backus G, Gilbert F. The Resolving Power of Gross Earth Data[J]. Geophys J R Astr Soc, 1968, 16: 169-205. DOI:10.1111/gji.1968.16.issue-2 |
| [15] |
Reginatto M. Resolving power of a multisphere neutron spectrometer[J]. Nucl Instr and Meth, 2002, 480: 690-695. DOI:10.1016/S0168-9002(01)01207-4 |



