屏蔽防护应用极广,在核工程和强源操作中,都要涉及到屏蔽问题。根据核技术工业应用涉及内容,γ射线源得到日益广泛应用和普及,γ射线源的放射防护屏蔽设计越来越受到放射卫生防护人员的重视与关注。
当研究宽束γ射线在物质中的减弱规律时,累积因子是描述散射光子影响的物理量。在辐射屏蔽设计中,累积因子的计算成为不可或缺的一部分,累积因子计算的差异,直接影响屏蔽设计的准确性。
1 计算方法在屏蔽设计时,累积因子是一个必须考虑的重要因素。在解决实际辐射防护问题时,采用经验公式法来计算累积因子,可使计算大为简化。在计算各向同性点源的屏蔽计算中,常用泰勒(Taylor)公式和伯杰(Berger)公式两种不同经验公式来计算累积因子。
1.1 泰勒公式| $ B = {A_1}{e^{ - {\alpha _1}\mu d}} + \left( {1 - {A_1}} \right){e^{ - {\alpha _2}\mu d}} $ | 1) |
式中,μ为线衰减系数,d屏蔽介质厚度,A1、α1、α2为与γ能量有关的常数,相关参数取值见表 1[1]。
|
|
表 1 用泰勒公式计算各向同性点源的累积因子的有关参数 |
| $ B = 1 + a\mu d{e^{b\mu d}} $ | 2) |
式中,μ为线衰减系数,d为屏蔽介质厚度,a、b为与γ能量有关的常数,相关参数取值见表 2[1]。
|
|
表 2 用伯杰公式计算各向同性点源的累积因子的有关参数 |
在屏蔽材料为铅时,根据公式(1)和公式(2),计算137Cs和60Co放射源在不同铅屏蔽厚度下的累积因子,计算结果见表 3。
|
|
表 3 各向同性点源的累积因子计算结果 |
根据表 3中对137Cs和60Co放射源在不同铅屏蔽厚度下的累积因子的计算结果,分别绘出137Cs和60Co放射源在不同经验公式计算下累积因子的比较图,见图 1和图 2。
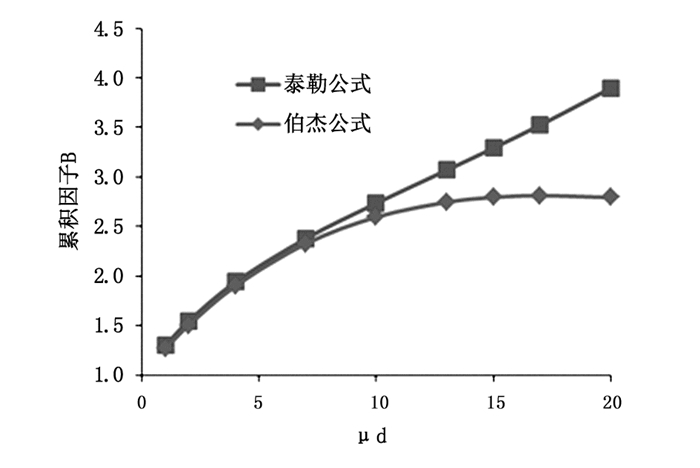
|
图 1 137Cs放射源在不同铅屏蔽厚度下的累积因子 |
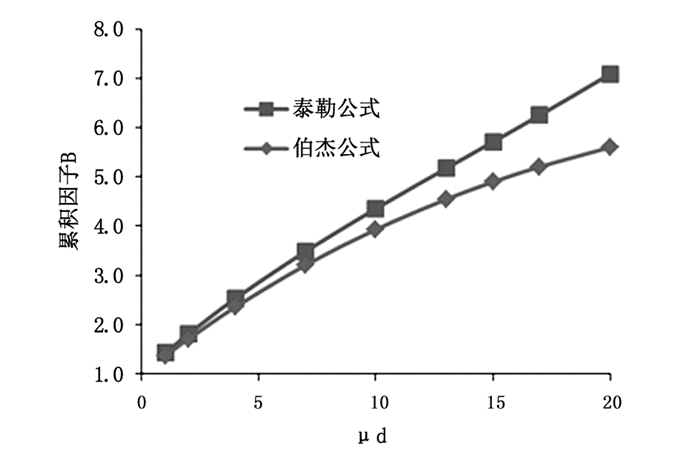
|
图 2 60Co放射源在不同铅屏蔽厚度下的累积因子 |
从图 1可知,对于137Cs放射源,μd在1~20之间时,累积因子随厚度的增加而增大;利用泰勒公式计算累积因子是利用伯杰公式计算累积因子的1~1.4倍;在辐射屏蔽设计中,μd在1~20之间时,利用伯杰公式计算137Cs放射源的累积因子所需屏蔽厚度较泰勒公式小。
从图 2可知,对于60Co放射源,μd在1~20之间时,累积因子随厚度的增加而增大;利用泰勒公式计算累积因子是利用伯杰公式计算累积因子的1~1.3倍;在辐射屏蔽设计中,μd在1~20之间时,利用伯杰公式计算60Co放射源的累积因子所需屏蔽厚度较泰勒公式小。
3 讨论综上所述,利用泰勒公式和伯杰公式计算累积因子时存在一定的差异。对于137Cs和60Co放射源,分别利用泰勒公式和伯杰公式计算累计因子时,可得出以下结论:①厚度越大,光子在介质中的散射贡献越大,累积因子也越大;②从对比结果可知,在同一屏蔽厚度下,利用泰勒公式计算结果均大于利用伯杰公式计算结果;③在辐射屏蔽设计中,μd在1~20之间时,利用伯杰公式计算137Cs和60Co放射源的累积因子所需屏蔽厚度较泰勒公式小。
| [1] |
李星洪. 辐射防护基础[M]. 北京: 原子能出版社, 1982: 118-129.
|


