加速器的充电电路是为仿真线充电的电路,因其要求的精度高,所以一般采取了一些措施,如常用的并联RC型DE-Q电路,当充电电路冲到设定值时,把充电电路切换到一个品质因素Q值较低的电路,然后以电阻发热的方式消耗掉充电电感中的剩余能量,为下一次充电把充电电感设置到零状态;充电完成后,PFN开关闭合,多充电电容(即PFN电容CN)放电,放电完成后,恢复到零状态。
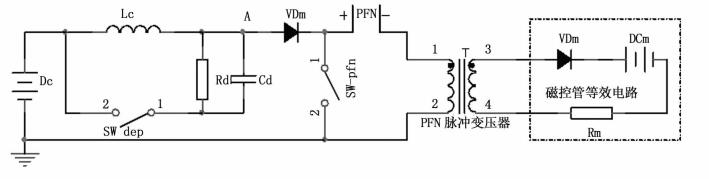
这两次开关的闭合,改变了电路结构,因充电电感感量大,如果不采取措施,如图 1所示,将出现如下一些问题:①充电精度降低;②隔离二极管和充电电感容易损坏;③DE-Q开关管、PFN开关管容易损坏等问题。
|
图 1 典型并联RC型DE-Q充电电路 |
|
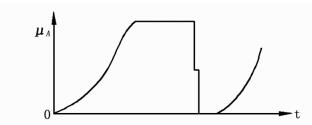
图 2 A点理想波形 |
|
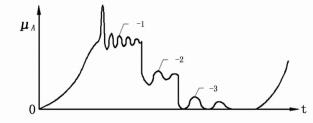
图 3 A点实测波形示意图 |
图 1充电电路固有震荡角频率为:
| $ {{\omega }_{c\text{ }o}}=\frac{1}{\sqrt{{{L}_{c}}{{C}_{N}}}} $ |
由图 3波形可看出与理想波形有三处不同,分别标注于图上1、2、3处。这三处的共同之处是:它们都是震荡衰减波形,且震荡频率都远大于充电波形频率;不同之处是:1处波形频率大约是充电波形频率的40~80倍,2、3处波形频率大约是充电波形频率的20~50倍。震荡波形意味着是二阶或二阶以上的电路产生,因频率不同所以产生的电路不同。
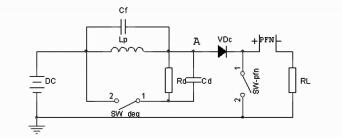
2 临界阻尼电路在隔离二极管的前级电路中,由于大电感存在匝间分布电容以及漏感,它们构成的等效电路为图 4:
|
图 4 考虑匝间分布电容以及漏感的电路 |
值得注意的是,这里的电感是Lp,而不是Lc。
在RLC并联谐振电路中,谐振条件为:
| $ R\le \frac{1}{2}\sqrt{\frac{L}{C}} $ |
在DE-Q电路设计时,一般Rd取比
| $ {{\omega }_{\text{d 0}}}=\frac{1}{\sqrt{{{L}_{\text{p}}}{{C}_{\text{f}}}}} $ |
|
图 5 第1处等效简化电路 |
比较
| $ \frac{{{\omega }_{\text{d 0}}}}{{{\omega }_{\text{c 0}}}}=\frac{\frac{1}{\sqrt{{{L}_{\text{p}}}{{C}_{\text{f}}}}}}{\frac{1}{\sqrt{{{L}_{\text{c}}}{{C}_{\text{N}}}}}}=\sqrt{\frac{{{L}_{\text{c}}}{{C}_{\text{N}}}}{{{L}_{\text{p}}}{{C}_{\text{f}}}}} $ |
其中:
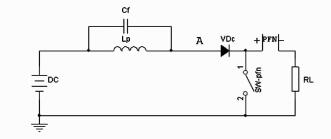
由图 5电路构成的并联RC振荡电路最大的问题是产生了很高的尖冲和高频震荡,所以需对上升的电压进行压制;同时破坏电路的震荡条件,而由RLC构成的临界阻尼等效电路就具备这个功能,如图 6:
|
图 6 临界阻尼等效电路 |
图 6中:
| $ {{R}_{\text{z}}}\le \frac{1}{2}\sqrt{\frac{{{L}_{\text{p}}}}{{{C}_{\text{f}}}}} $ |
一般取其1/3-1/10之间,使其可靠地不会处于震荡状态。
功耗大约等于临界阻尼电容的储能:
| $ {{P}_{{{\text{R}}_{\text{z}}}}}\approx {{C}_{\text{z}}}E_{0}^{2}{{f}_{\text{r}}} $ |
可取1.5PRz的功耗。
这样的电路解决了阻尼的问题,但带来了对充电电路的影响,对此进行修正,在阻尼电阻支路上串入电容,此电容不会对原有的分布电容造成影响,一般取值为:Cz≥3Cf,这里取值为:
| $ {{C}_{\text{z}}}=5\sim 10{{C}_{\text{r}}} $ |
耐压:实际电压为E0多一点,考虑余量,取2E0耐压值。
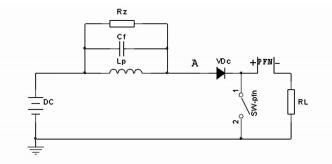
图 7为由此修正的临界阻尼等效电路。
|
图 7 完整的临界阻尼等效电路 |
通过临界阻尼电路处理后波形变为图 8:

|
图 8 临界阻尼电路处理后波形 |
由测试波形消除了第一处的尖峰和震荡,证实了以上分析,并取得很好的效果。
3 反尖峰电路在使用了临界阻尼电路后,第1处的波形变好,但在第2、3处基本没有改变,说明此处的波由另外的电路产生。而2、3处波形频率基本相当,可以猜想是同一电路产生。
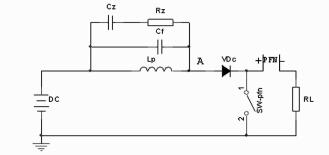
当SW_pfn开通时,充电电感的对地分布电容C0通过隔离二极管极速放电,破坏了隔离二极管左边的电路的稳定性,由充电电感的对地分布电容C0和漏感Lp构成了串联LC震荡电路,如图 9:
|
图 9 SW_pfn开通时隔离二极管右边等效电路 |
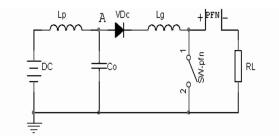
图 10串联LC电路固有震荡频率为:
| $ {{\omega }_{\text{g }0}}=\frac{1}{\sqrt{{{L}_{\text{p}}}{{C}_{0}}}} $ |
|
图 10 增加阻尼电感的电路 |
比较
| $ \frac{{{\omega }_{\text{g }0}}}{{{\omega }_{\text{c }0}}}=\frac{\frac{1}{\sqrt{{{L}_{\text{p}}}{{C}_{0}}}}}{\frac{1}{\sqrt{{{L}_{\text{c}}}{{C}_{\text{N}}}}}}=\frac{\sqrt{{{L}_{\text{c}}}{{C}_{\text{N}}}}}{{{L}_{\text{p}}}{{C}_{0}}} $ |
其中:
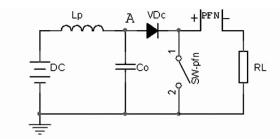
此电路工作的原因在于C0的极速放电,极大的破坏了电路的平衡,如果能降低这种变化,此电路的波形将得到改善。设想一个减缓C0放电速度的电路,电感具备这种功能,串接到C0的放电回路中,如图 10。
Lg的选取原则:对高频的放电产生作用,而对低频的充电基本不产生作用。选取充电回路中充电电感Lc的0.5%~2%,一般选取1%。
在充电时Lc、Lg的感抗分别为:
| $ {{Z}_{\text{cc}}}=2\text{ }\!\!\pi\!\!\text{ }{{f}_{\text{r}}}{{L}_{\text{c}}}~\ \ {{Z}_{\text{gc}}}=2\text{ }\!\!\pi\!\!\text{ }{{f}_{\text{r}}}{{L}_{\text{g}}}=0.012\text{ }\!\!\pi\!\!\text{ }{{f}_{\text{r}}}{{L}_{\text{c}}} $ |
而由C0和Lg组成的电路震荡频率和在为此频率下Lg的感抗分别为:
| $ {{f}_{\text{g}}}=\frac{1}{2\pi \sqrt{{{C}_{0}}{{L}_{\text{g}}}}}\text{ }\!\!~\!\!\text{ }\ \ {{Z}_{\text{gg}}}=2\pi {{f}_{\text{g}}}{{L}_{\text{g}}} $ |
两者阻抗之比为:
| $ {{Z}_{\text{gc}}}{{Z}_{\text{gg}}}=\frac{2\pi {{f}_{\text{r}}}{{L}_{\text{g}}}}{2\pi {{f}_{\text{g}}}{{L}_{\text{g}}}}=\frac{{{f}_{\text{r}}}}{{{f}_{\text{g}}}}=\frac{\frac{1}{2\pi \sqrt{{{C}_{\text{N}}}{{L}_{\text{c}}}}}}{\frac{1}{2\pi \sqrt{{{C}_{0}}{{L}_{\text{g}}}}}}=\sqrt{\frac{{{C}_{0}}{{L}_{\text{g}}}}{{{C}_{\text{N}}}{{L}_{\text{c}}}}}\approx \frac{1}{10}\sqrt{\frac{{{C}_{0}}}{{{C}_{\text{N}}}}} $ |
此值大约在1:50到1:70之间。
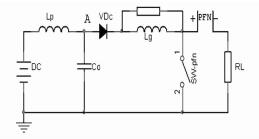
在增加了阻尼电感Lg后将C0上的能量转移给了Lg,这将影响PFN电路的波形,为了降低这种影响,与Lg并联一个阻尼电阻Rg来消耗这个能量,如图 11:
|
图 11 完整的尖峰阻尼电路 |
Rg的选取:
阻值:Zgc≤Rg<Zgg
功耗:PRg≈4C0e02fr,一般取其1.5倍。
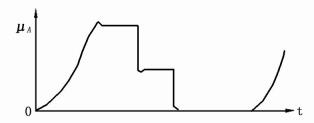
调整后的波形为图 12,由测试波形证实了以上分析,并取得很好的效果。
|
图 12 尖峰阻尼电路处理后波形 |
至此,完整的脉冲调制器的调整完成,如图 13:

|
图 13 调整完成的脉冲调制器 |
加速器的脉冲调制器充电电路是一个比较复杂的电路,以上的分析是突出电路的主要因素进行分析,如果要进行精确分析需借助于模拟软件等措施,但这种分析已经基本够用,在实际的辅助电路设计和验证中已经得到了很好的验证。另外,以上的计算是建立在一定范围内的经验值的基础上的,对于具体的电路应根据实际情况进行确定。
| [1] |
郑新, 李文辉, 潘厚忠. 雷达发射技术[M]. 北京: 电子工业出版社, 2006.
|
| [2] |
强伯涵, 魏智. 现代雷达发射机的理论设计与实践[M]. 北京: 国防工业出版社, 1985.
|
| [3] |
东冲. 线型脉冲调制器理论基础和专用电路[M]. 北京: 国防工业出版社, 1978.
|


