环境中的氚主要来自核反应堆燃料的三裂变以及核材料的中子活化。84% ~ 97%的氚以氚化水形式释出,2% ~ 3%以氚化水蒸气形式释放,0.6% ~ 8%以氚气形式释放[1]。核电站工作人员易暴露在氚污染环境中,虽然氚的外照射危害不大,但是氚水和氚水蒸气容易通过皮肤或呼吸道进入工作人员体内,所致内照射严重危害工人的健康[2-3]。尿氚活度浓度是工作人员受氚内照射污染严重程度的重要指标[4],液闪测量法是尿氚分析的常用方法[5-7],但是现有尿氚分析的国家标准方法制订于上世纪90年代[8],结果均未涉及不确定度,这使尿氚分析缺乏对系统误差、偶然误差和技术水平的综合判断,无法表达分析结果接近真值的程度。虽然国内外也有少数文献对水中氚检测的不确定度评估进行了探讨[9-11],但是很少涉及尿氚分析不确定的报道。本文根据本实验室尿氚分析结果[1],以秦山核电站工作人员尿样中氚的活度浓度为例,进一步开展了不确定度评价,使尿氚分析结果得到了完整、科学的表达,该不确定度评估过程能够为相关国家标准的修订提供参考。
1 尿氚的分析过程 1.1 仪器和试剂液体闪烁计数仪(Perkin Elemer TRI-CARB 3170 TR/SL BASE,美国); 分析天平(Mettler Toledo PL602-S); 圆底烧瓶(500 mL),低钾玻璃瓶(20 mL)和聚乙烯瓶(20 mL); 过硫酸钾(≥99.5%,ACROS)。闪烁液(ULTIMA GOLDTM LLT,PerkinElmer); 本底水为市售电导率小于4 μs/cm桶装蒸馏水; 活度浓度为150 Bq/mL的标准氚水(不确定度2.4%,中国计量院)。
1.2 样品制备 1.2.1 待测样品制备取50 mL尿样于250 mL蒸馏瓶中,加入10 g过硫酸钾,加热。当样液开始起泡沫时,控制温度保持近沸,氧化回流20 min。接着升温蒸馏,蒸馏液流出3 ~ 5 mL后,用聚乙烯瓶收集余下蒸馏液备用。取8 mL蒸馏液和12 mL闪烁液,放入20 mL样品计数瓶中,旋紧瓶盖,振荡混合均匀后避光保存备用。
1.2.2 本底样品制备将本底水按1.2.1步骤进行蒸馏,取8 mL蒸馏液和12 mL闪烁液,放入到20 mL样品计数瓶中,旋紧瓶盖,振荡混合均匀后避光保存备用。
1.2.3 标准样品制备取8 mL氚标准水溶液和12 mL闪烁液,放入到20 mL样品计数瓶中,旋紧瓶盖,振荡混合均匀后避光保存备用。
2 尿氚结果分析待测样品来自秦山核电站4名工作人员的尿液[1]。样品经前处理、加闪烁液、避光放置数天后在液闪上的计数率如表 1所示。待测样品计数、本底样品计数、标准氚水计数率如下表 1所示。
|
|
表 1 待测样品、本底样品、标准样品的计数率、活度浓度和标准偏差 |
根据标准样品的测量值,液闪对氚的探测效率为:

|
(1) |
式中: E是探测效率; nd为标准样品计数率; nb为本底计数率; D为校准后的标准活度浓度。
代入表 1中相应数值得液闪的探测效率为:

|
样品活度浓度的计算公式[8]为:
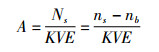
|
(2) |
式中: A为样品的活度浓度; ns为样品计数率; nb为本底计数率; Ns为样品净计数率; K为单位换算系数; V是测量所用样品蒸馏液体积; E为探测效率。
代入各样品测量数据,即得到1 ~ 4号样品的活度浓度,如表 1所示。
3 不确定度评价从尿氚活度浓度的计算公式(2),即不确定度数学模型,可以看出影响不确定度的主要参数有ns、nb、V和E,因此,尿氚不确定度的来源包括样品β测量不确定度、取样体积不确定度和探测效率不确定度。不确定度来源的因果关系见图 1。

|
图 1 不确定度来源的因果关系 |
由于不确定度数学模型中各参数之间相互独立,尿氚活度浓度的合成相对不确定度和各相对不确定度分量之间的关系可以表达为[12]:

|
(3) |
下面将逐一介绍各不确定分量的计算。
3.1 β测量不确定度urel(Ns)β测量不确定度即为样品净计数率的相对误差,计算公式为:

|
(4) |
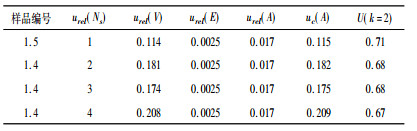
代入数据,得1 ~ 4号样品净计数的相对不确定度分别为0.114、0.181、0.174、0.208。
3.2 体积不确定度urel (V)测量时样品瓶中加了8 mL样品蒸馏液,操作时用5 mL的移液器量取了两个4 mL。该移液器的校准不准确度为± 0.012 mL,校准不精密度为± 0.003 mL。按均匀分布换算,准确度标准偏差为0.012/
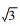

|
所以,1 ~ 4号样品体积相对不确定度均为0.0025。
3.3 探测效率不确定度urel(E)探测效率实验中移取了1 mL标准氚水参与效率的评估,结合公式1可知,仪器的探测效率不确定度由标准氚水的净计数统计误差、标准氚水的校准不确定度、1 mL移液器的体积不确定度组成,另外还包括探测效率的不稳定性不确定度。
3.3.1 标准氚水的β测量不确定度u31根据公式(4),标准氚水的β测量不确定度为:
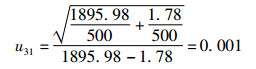
|
经中国计量院校准,标准氚水的校准不确定度为2.4%,按均匀分布计算,该标准氚水的相对不确定度为:
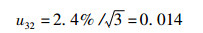
|
探测效率实验中移取了1 mL标准氚水,操作时使用了1 mL的移液器。该移液器的校准不准确度为± 0.006 mL,校准不精密度为± 0.002 mL。按均匀分布换算,准确度标准偏差为0.006/
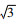
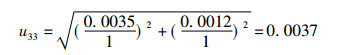
|
由于仪器的不稳定,同一标准氚水在不同时间在同一液闪仪中测得的净计数不尽相同,得到的探测效率也有一定的差别,表 2给出了6次测量仪器的探测效率。
|
|
表 2 6次测量仪器的探测效率 |
因此,探测效率的平均值为,其不稳定性的相对不确定度为:
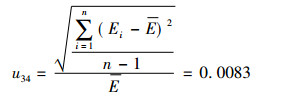
|
综上,探测效率合成不确定度为:

|
根据各不确定分量和公式(3),可以合成尿氚活度的相对不确定度。例如,1号样品的合成相对不确定度为:

|
同理可以得到urel (A2)、urel (A3)、urel (A4)的值。标准不确定度uc(A) = A·urel(A),当扩展因子k取2时,扩展不确定U可以根据U = k·uc (A)算出。修约后计算结果详见表 3。
|
|
表 3 样品的相对不确定度分量、合成不确定度和扩展不确定度 |
由上述各不确定度分量可以看出,尿氚活度浓度总不确定度主要来源于β计数的统计误差,从1 ~ 4号样品分析,样品计数率越大,β统计误差不确定度越小。探测效率不确定度和体积不确定度对总不确定的贡献较小,当样品计数率接近本底时,二者对不确定度的贡献可以忽略。
由不确定度评估结果可知,4个样品尿氚的相对不确定度分别为11.5%、18.2%、17.5%和20.9%。综合1 -4号样品尿氚的分析,当扩展因子k取2时,1 ~ 4号样品的测量结果表达为(6.2 ± 1.5) Bq/L、(3.8 ± 1.4) Bq/L、(3.9 ±1.4) Bq/L、(3.2 ±1.4) Bq/L。分析结果±不确定度,才是尿氚测量结果科学、完整的表达。
| [1] |
Shen Bao Ming, Ji Yan Qin, Tian Qing, et al. Determination of Total Tritium in Urine from Residents Living in the Vicinity of Nuclear Power Plants in Qinshan, China[J]. Int. Journal of Environmental Research and Public Health, 2015, 12: 888-894. DOI:10.3390/ijerph120100888 |
| [2] |
马加一, 徐小三, 杨小勇. 氚内照射的检测和评价方法[J]. 江苏预防医学, 2013, 24(1): 38-39. DOI:10.3969/j.issn.1006-9070.2013.01.015 |
| [3] |
韩佩珍, 张景源. 24例非职业照射者尿中氚浓度[J]. 中华放射医学与防护杂志, 1981, 1(6): 43-44. |
| [4] |
赵秋芬, 刘岩. 人尿氚的半减期及内照射剂量估算[J]. 中华放射医学与防护杂志, 1994, 14(6): 410-411. |
| [5] |
苏锋, 花威, 郑传城, 等. 尿中氚含量的两种测定方法及比较[J]. 中国辐射卫生, 2009, 18(3): 280-281. |
| [6] |
王兰新, 张太明, 阮光林, 等. 尿中氚水和总氚的分析测定[J]. 核化学与放射化学, 2003, 25(4): 249-252. DOI:10.3969/j.issn.0253-9950.2003.04.012 |
| [7] |
张彩虹, 问清华, 陈克非, 等. 用直接液闪法测定尿氚浓度[J]. 辐射防护, 1999, 19(6): 444-448. |
| [8] |
中华人民共和国标准. EJ /T 1047-1997尿中氚的分析方法[S].北京: 核工业标准化研究所, 1997.
|
| [9] |
张向阳, 陈宗宇, 刘福亮, 等. 水中氚放射性活度分析的不确定度评定[J]. 核电子学与探测技术, 2010, 10: 1318-1322. DOI:10.3969/j.issn.0258-0934.2010.10.011 |
| [10] |
Gröning M, Rozanski K. Uncertainty assessment of environmentaltritium measurements in water[J]. Accred Qual Assur, 2003, 8: 359-366. DOI:10.1007/s00769-003-0631-y |
| [11] |
IAEA. Quantifying uncertainty innuclear analytical measurements [R]. Vienna: International Atomic Energy Agency, 2004: 195 - 218.
|
| [12] |
JCGM Evaluation of measurement data-Guide to the expression of uncertainty in measurement[S]. Joint Committee for Guides in Metrology, 2008.
|