依照GB6566-2001《建筑材料放射性核素限量》, 放射性核素钾-40做为建材中一个重要指标, 其测量方法主要采用γ能谱法, 但由于能谱仪价格昂贵, 而且日常维护成本高, 许多基层实验室还是采用化学法。由于在分析建材的放射性时, 前处理比一般化学分析复杂, 处理样品时, 试剂用量大, 操作步骤多, 故带来的不确定因素也较多^[1]。本法主要采用KCl标准系列, FE-883B火焰光度计回归标准曲线, 计算钾含量。根据1 g天然钾中钾-40的放射性强度为28.1 Bq, 可以计算样品中的放射性钾的活度。本法主要通过采用鱼骨图法分析建材中钾测量的不确定度, 分析计算公式中的有关参数, 在分析建材中钾时, 主要受到测量仪器、标准物、样品取样体积极及称重等不确定度因素的影响。

1 实验材料^[2] 1.1 仪器与试剂

FE-883B火焰光度计(中国广州分析测试中心), 氯化钾标准(国家标准物质研究中心), 高氯酸, 氢氟酸, 盐酸。

1.2 仪器操作条件

采用空心阴极灯, 液化石油气-空气等低温火焰(约1900℃), 仪器的雾化器、提升量、燃烧器位置、火焰根据具体操作调节。狭缝、灯电流由厂家调好。

1.3 标准系列配制

准确称取0.9535 g经105℃烘干的氯化钾(基准试剂)液于500.0ml容量瓶中, 用纯水定容到刻度, 此液浓度为1.00 mg/mL的标准使用液。用0.5 ml的移液管分别吸取0.00, 0.10, 0.20, 0.30, 0.40, 0.50 ml标准使用液(1.00 mg/ml)于100.0 ml容量瓶中, 用0.1 mol/L的HCl定容到刻度, 此标准系列的浓度系列为(0.0, 1.0, 2.0, 3.0, 4.0, 5.0 μg/ml)。

1.4 样品处理与测定

准确称取0.2000 g已经研磨的建材样品于聚四氟已烯坩埚内, 加水湿润, 再加入2 ml高氯酸, 10 ml氢氟酸, 置沙浴中在电炉上缓慢加热, 使样品分解, 继续加热蒸干并冒白烟。加入10 ml 1:1HCl, 温热使残渣溶解, 转移到100ml容量瓶中, 定容到刻度。使用FE-883B火焰光度计, 先测出标准系列的火焰光度, 绘制出火焰光度与浓度关系的标准曲线。然后测量样品溶液的火焰光度, 在校准曲线上可计算样品溶液中钾的浓度。

2 试验方法 2.1 数学模型

依据分光光度计中检出限计算公式建立数学模型标曲线回归方程:Y=a+bX

式中, Y-吸光度值(A); X-浓度值(μg/ml); a -截距; b-斜率。

钾含量C(μg/g)为:

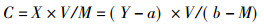
(1)

式中, V-定容体积(ml); M-样品质量(g)。

合成不确定度根据式(1)和不确定度传播定律^[3]可得到被测量C的合成不确定度U_c(C):

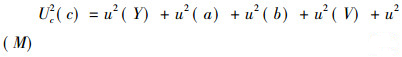
(2)

式中, U_c(C)-样品中钾含量测定的合成不确定度; u(Y)-火焰光度值Y的标准不确定度; u(a)-截距a的标准不确定度; u(b)-斜率b的标准不确定度; u(V)-定容体积V的标准不确定度; u(M)-样品质量M的标准不确定度。

2.2 不确定度计算与分析 2.2.1 火焰光度Y的标准不确定度u(Y)

火焰光度Y的标准不确定度u(Y)由吸光度Y的标准差S_y/x和所使用钾标准溶液的不可靠性对Y产生的不确定度u(Y₂)两者组成, 即:

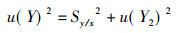
(3)

2.2.1.1 吸光度Y的标准差S_y/x

用火焰光度仪测得的标准系列吸光度如表 1所示。

由上表采用最小二乘法线性回归求得r= 0.9995, a=-2.4, b=6.2, 则回归曲线方程为

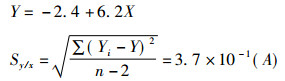
(4)

2.2.1.2 使用钾标准使用液的不可靠性对Y产生的不确定度u(Y₂), =0.5×u(Y₂)

(5)

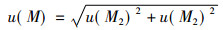
(6)

u(M)为称量标准引起的不确定度, u(v₁) u(v₂)分别为500 ml A级容量瓶的相对标准不确定度和0.5 ml A级移液管的不确定度。u(M₁)为称取氯化钾标准的天平的不确定度, u(M₂)为天平重复称样误差引起的不确定度, 计算所使用的钾的不可靠性对吸光度Y所产生的不确定度u(Y₂), =0.5x u(Y₂), 0.5为标准曲线钾含量的最大取样体积(ml)。

2.2.1.3 称量不确定度

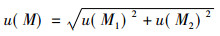
(7)

因为标准是用减量法称量, 所以:u(M₁)=u_天平/km_器皿, u(M₂)=u_天平/k(m_s1+m_器皿)由天平检定证书查得:u_天平=0.3 mg, K=2, 实验中, m_器皿=23687.5 mg, m_s1=953.5 mg故u(M)=3.5×10^-6g。

2.2.1.4 500.0 ml A级容量瓶的相对不确定度^[4]

500.0ml A级容量瓶的标准不确定度包括允许误差u (V_A)、充液重复性误差u(V_B)和温度变化产生误差u(V_C), 即:

(8)

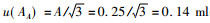
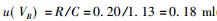
式中: (B类不确定度, 500.0 ml A级容量瓶允许误差查书为A=± 0.25 ml)。

(A类不确定度。用极差法计算, 充液两次, 其极差R=0.20ml)。

(A类不确定度, 设温度变化±3℃, 水的膨胀系数在20℃时a=2.1×10^-4/℃)。

由式(8)可以算得500.0 ml容量瓶的标准不确定度u(V)=0.22 ml。则其相对标准不确定度u(v₁)/500=4.4×10^-4。

2.2.1.5 0.5 ml A级移液管的相对不确定度^[4]

0.5 ml移液管的移液不确定度U₁为0.0007 ml, 扩展系数K=2, 则移液不确定度为U_A=U₁/(2 × 0.5)=7×10^-4, 20℃温度校准, 实验室的温度在± 3℃变化, 受膨胀系数作用影响可引起液体体积变化, 水的体积膨胀系数为水的膨胀系数在20℃时=2.1×10^-4/℃, , 所以, u²(v₂)=u²(v_A)+u²(v_B)u(v₂)=7.0×10^-4。

根据式(5)u(Y₂)=0.5×5.7×10^-4=2.85×10^-4。

根据式(3) 。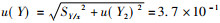

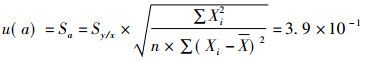
2.2.2 截距a的不确定度u(a)(即a的标准差S_a)

(9)

2.2.3 斜率b的不确定度u(b)(即b的标准差S_b)

(10)

2.2.4 定容体积V的标准不确定度u(V)

100.0 mlA级容量瓶的标准不确定度包括允许误差u(V_A)、充液重复性误差u(V_B)和温度变化产生误差u(V_C), 即:

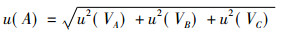
(11)

式中: 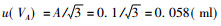(B类不确定度, 100.0 ml A级容量瓶允许误差查书为A= ±0.10ml)。

u(V_B)=R/C=0.10/0.113=0.088(ml)(A类不确定度。用极差法计算, 充液两次, 其极差R=0.10 ml)。

(ml)(A类不确定度, 设温度变化± 3℃, 水的膨胀系数在20℃时a=2.1×10^-4/℃)。

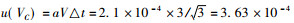
由式(16)可以算得100.0 ml容量瓶的相对标准不确定度u(V)=0.12。

2.2.5 样品质量M的标准不确定度u(M)

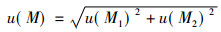
(12)

因为样品源是用减量法称量所得所以:u(M₁)= u_天平/km_器皿, (M₂)=u_天平/k(m_s1+m_器皿)由天平检定证书查得:u_天平=0.3 mg, K=2, 实验中, m_器皿=23 687.5mg, m_s1=200 mg故u(M)=1×10^-5。

3 实验结果 3.1 合成不确定度Uc(C)

有关各量代入式(2)得:

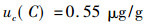
(13)

扩展不确定度

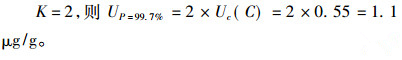
(14)

4 讨论

不同参数的不确定度比较见表 2。

实验过程中影响样品测量的不确定因素很多, 对总不确定度的贡献各有不同, 由上表看出, 最大的不确定度分量是直线回归曲线Y及截距a、斜率b引入的, 由于火焰光度计测量装置测量不确定度的原理是由雾化器将试样喷入火焰, 激发发光, 经分光后由检测器测量发射强度, 后者与试样中待测元素含量成正比。主要受以下几方面影响:①火焰温度:温度过低灵敏度下降, 温度太高则碱金属电离严重, 影响测量的线性关系。影响火焰温度的因素有燃气种类、燃气与助燃气比例。试样溶液抽吸量过大时会使火焰温度下降。②气体压力:测定时气体压力需保持恒定。③喷雾器:喷雾器不清洁, 易造成试液雾化不良, 测定时一定要求试液清亮, 并随时用水或乙醇清洗喷雾器。④液面高度:液面高度变化, 会引起激发后的元素浓度有变化, 测定时需保持试验高度一致。由于多因素影响, 测量结果的不确定度也相对较大。由标准溶液、样品溶液配制引起的不确定度分量, 主要表现在定容体积V的标准不确定度中, 对不确定度也有所影响。样品的称量不确定度可以基本忽略。