2. 中国安科院尘毒危害预防与控制技术实验室
X、γ射线与物质相互作用,其能量损失一般有光电效应、康普顿散射、电子对效应、瑞利散射、光核反应等过程[1]。X、γ射线进入物质后,主要经上述的各种作用过程被吸收和散射,其相互作用总截面为
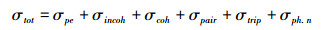
|
(1) |
物质对X、γ射线线性衰减系数可以表述为[2]
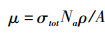
|
(2) |
Na为阿佛加德罗常数,ρ为物质质量密度,A为物质的原子量。
入射X、γ射线能量为80 ~ 1000 keV范围内,主要发生光电效应和康普顿散射,和占很小一部分比例的瑞利散射[2-4],一般可以将(2)式简化为[4],
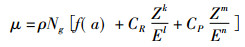
|
(3) |
式中CR、CP分别为瑞利散射和光电效应常数,Ng为物质质量电子密度,ρ为物质质量密度,Z为原子序数,E是光子的能量,单位是keV。康普顿散射的相互作用截面一般用Klein-Nishina函数表述[5]

|
(4) |
有人在诊断X射线能量范围内(80 keV-120 keV),通过对低原子序数物质的实验精确测量[6],测得式(3)相关参数为,瑞利散射和光电效应常数CR = 1.25 × 10-24,CP = 9.8 × 10-24,k = 2.0,L = 1.9,m = 3.8,n = 3.2。在此条件下,式(4)可以精确的简化为
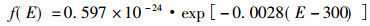
|
(5) |
本研究选用NIST提供的入射能量为80 keV ~ 1000 keV的X、γ射线与1 ~92号元素相互作用的线性衰减系数[6-7],对公式(3)的相关参数进行修正。修正方法为,利用氢元素与80 keV ~ 1000 keV X、γ射线相互作用时,主要考虑康普顿散射的影响[4],对康普顿散射随能量递增的相关参数进行修正。随后,分别选用80 ~ 1000 keV的不同能量值入射X、γ射线,对光电效应相关参数随能量和物质原子序数递增进行修正。
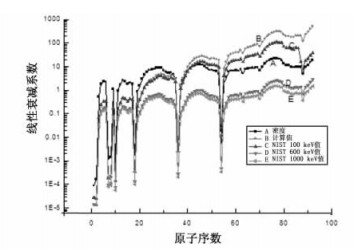
2 分析和结果选用100 keV入射X、γ射线,利用公式(3)计算1 ~ 92号元素的线性衰减系数,其计算结果详见图 1的B曲线。图 1中的A、C、D、E曲线分别为NIST的参考数据库提供的1 ~ 92号元素的质量密度和100 keV、600 keV、1000 keV入射能量的线性衰减系数。由图 1分析可知,由公式(3)计算值(曲线B),与NIST提供的值(曲线C、D、E)以几乎相同的趋势变化,在低原子序数部分,B、C两条曲线几乎重叠,在高原子序数部分出现较大的分离。说明此计算公式主体是正确的,但其相关参数要随原子序数和入射X、γ射线能量的递增进行修正。
|
图 1 不同能量入射X、γ射线与1-92号元素作用线性衰减系数变化曲线 |
一般认为康普顿效应为光子与自由电子(外层电子的结合能远小于光子能量)发生散射,光子的部分能量转移给电子(康普顿电子),而散射光子改变其能量和方向。入射能量为80 ~ 1000 keV的X、γ射线与氢元素相互作用,其光电效应和瑞利散射的截面远低于康普顿散射截面,完全可以忽略光电效应和瑞利散射的影响,只考虑康普顿散射的影响[3]。
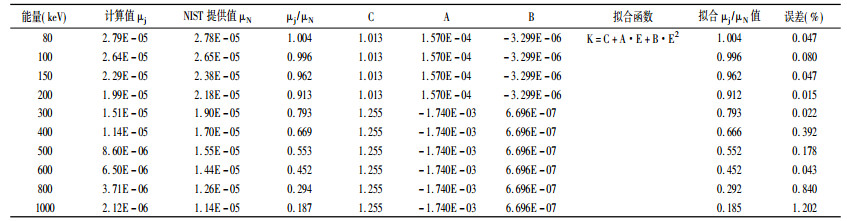
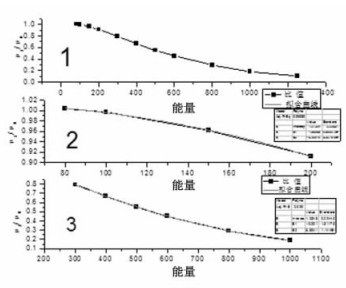
利用(3)计算80 ~ 1000 keV X、γ射线与氢元素相互作用的线性衰减系数,具体计算结果见表 1的μj,NIST提供值为μN,将μj /μN,具体比值见表 1,将μj /μN值作图,见图 2的1曲线。由1曲线分析可知,μj /μN值在300 keV附近出现转折,在此之前和之后的曲线变化趋势分别一致。取80 ~ 300 keV和300 ~ 1000 keV两段分别作图,见图 2的2、3曲线,利用二次函数分别拟合两条曲线,具体拟合函数为K = C + A* E + B* E2,各参数见表 1。由以上分析可知,在X、γ射线80 ~ 1000 keV能量范围内,康普顿散射的计算公式应修正为:
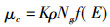
|
(6) |
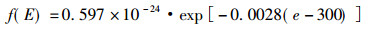
|
(7) |
|
|
表 1 氢元素随入射X、γ射线能量递增的康普顿散射系数修正情况 |
|
图 2 氢元素的康普顿散射能量变化曲线 |
式中ρ为物质的密度,Ng为质量电子密度。康普顿散射的修正系数K为80 keV-300 keV和300 keV-1000 keV两段分别取值,详见表 1。
2.2 光电效应参数修正 2.2.1 公式(3)相关参数m的修正X、γ射线与物质相互作用,其光电效应主要决定于物质的原子序数Z和入射X、γ射线的能量E[1, 5]。将公式(7)代入公式(3)中,参数n取定值3.2,以NIST提供的数据作为参考,选择最佳的与原子序数相关的m值。
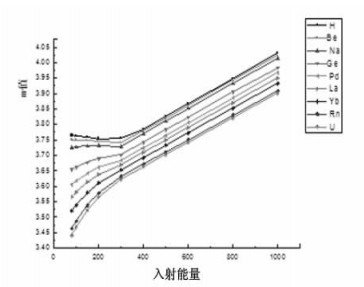
随机选取九种元素随能量递增的m值作图,见图 3。由图 3分析可知,随着能量的递增,各元素的各能量点m值随能量的递增成线性关系,在300 keV附近出现转折。在300 ~ 1000 keV范围内,各能量点参数m值随原子序数的递增变化趋势几乎相同; 在80 ~ 300 keV范围内,各能量点参数m值随原子序数的递增变化趋势不完全相同。
|
图 3 几种元素的参数m随入射光子能量变化曲线 |
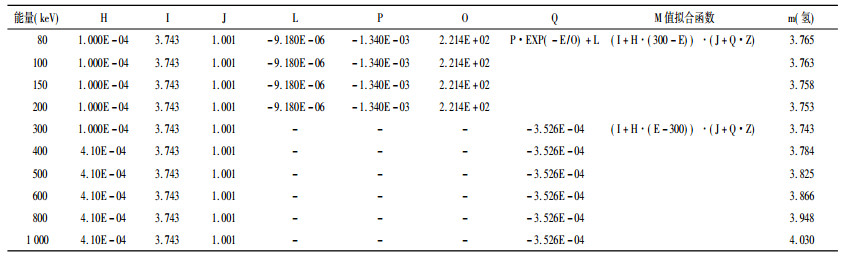
选择80 keV ~ 1000 keV范围内各能量点氢元素的参数m值作图,见图 4的1曲线。分别选择80 ~ 300 keV和300 ~ 1000 keV两个能量范围的m值作图,见图 4的2、3曲线。分别对2、3两曲线线性拟合,拟合函数及相关参数见表 2,在80 ~ 300 keV范围内,m = I + H·(300-E),在300 ~ 1000 keV范围内,m = I + H·(E-300),I和H须分段选择,见表 2。

|
图 4 氢元素的光电效应m值随能量变化曲线和分段拟合曲线 |
|
|
表 2 1 ~ 92号元素参数m随能量和原子序数递增的修正情况 |
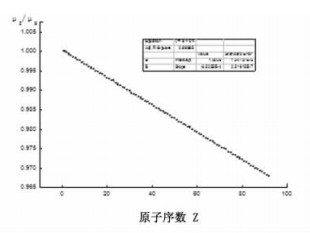
对参数m随原子序数递增的修正也需分段研究。选择600 keV能量点1 ~ 92号元素的各个m值,将各元素的m值与氢元素的m值比较,比值为mz/mH,随原子序数的递增,将各元素的mz/mH作图,用线性拟合,见图 5。拟合函数和相关参数见表 2,此能量点m值随原子序数递增的修正系数H = J + K·Z。由图 3分析,300 ~ 1000 keV范围内,各能量点的m值随原子序数递增的变化趋势相同,可以将600 keV能量点的m值随原子序数递增的修正系数(H = J + K·Z)直接应用于300 ~ 1000 keV能量范围。
|
图 5 600 keV能量点m值随原子序数递增变化曲线 |
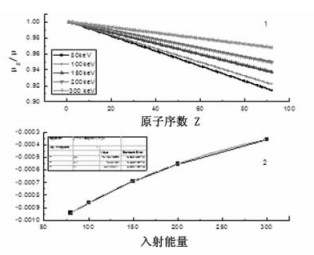
对80 ~ 300 keV范围内的各能量点分别进行修正,具体各能量点随原子序数递增的修正值见图 6的1曲线,由此曲线分析可知,各能量点的m值随原子序数的递增都几乎分别成直线关系,但各直线的变化趋势各不相同。由此分析可知,各能量点的m值随原子序数递增的修正直线的斜率与能量具有相关性。用直线拟合各能量点的m值与原子序数递增的变化曲线,取各能量点拟合直线的斜率作图,见图 6的2曲线,用指数函数拟合,拟合的函数和相关参数见表 2,斜率修正系数Q = P·EXP(-E /O) + L,E为入射X、γ射线的能量,参数P、O、L值详见表 2。
|
图 6 80 ~ 300 kev内各能量点m随原子序数递增变化曲线和系数Q的修正曲线 |
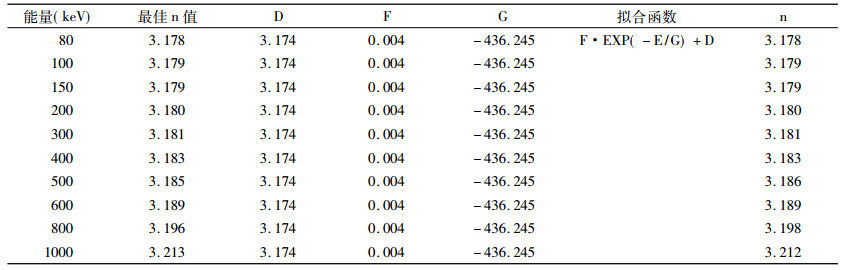
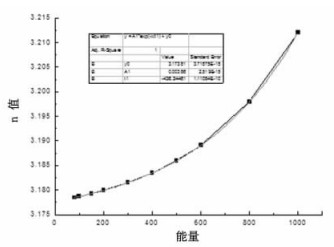
将上文所修正的各个参数代入公式(3),以NIST提供的相应值作为参考,选取各能量点各元素所对应的最佳n值。对所有的n值分析发现,在某一能量点,n值随原子序数的递增几乎为一定值,不同的能量点的n值各不相同,将各个能量点的最佳n值作图,见图 7。用指数拟合,拟合函数及相关参数见表 3,n值的拟合函数为F* EXP(- E /G) + D,E为入射X、γ射线的能量,参数F、G、D的值详见表 3。
|
图 7 参数n随能量变化曲线 |
|
|
表 3 各能量点参数n的能量修正 |
通过上文研究和分析,一定能量(80 ~ 1000 keV)的入射X、γ射线与物质相互作用,其能量的衰减主要决定于康普顿散射和光电效应。随着射线能量和原子序数的递增,公式(3)应对其相关参数修正为如下:
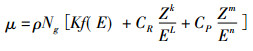
|
(9) |
式中的Z为原子序数; E是光子的能量,单位是KeV; f(E)是取决于光子能量的康普顿散射函数,f (E) = 0.597 × 10-24·exp[-0.0028(E-300)];
CR、= 1.25 × 10-24,CP = 9.8 × 10-24分别是与瑞利散射和光电吸收有的常数; Ng是每克物质中的电子质量密度; 式中各参数(K、m、n)的修正情况详见表 4; 瑞利散射各相关参数未作修正,k = 2.0,L = 1.9。
|
|
表 4 X、γ射线与物质相互作用的计算公式相关参数修正 |
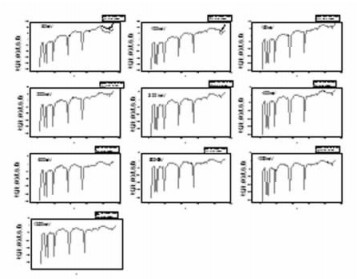
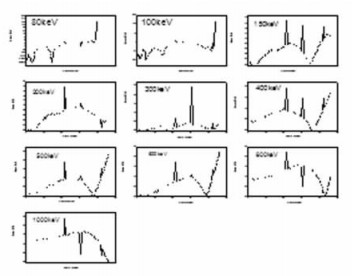
利用公式(9)计算各能量点1 ~ 92号元素的线性衰减系数μJ,选择NIST提供的相应数据μN,见图 8。由图 8可见,150 ~ 1000 keV的所有研究点能量的计算衰减系数值μJ和NIST提供的相应数据μN,随原子序数变化的曲线几乎重叠。80 keV和100 keV两个能量值,在低原子序数部分(分别为79和87号以下) μj和μN几乎重叠,但在高原子序数部分出现了较大的分离。将公式(9)计算值与NIST提供的相应值的偏差(%),随着原子序数递增作图,见图 9。由图 9分析可知,80 ~ 1000 keV的所有元素的计算值与NIST提供的相应值的偏差几乎都在2%以内(除43、61、84号元素)。能量为100 keV时,87 ~ 92号元素的偏差明显增加,最大偏差达277.4 %,能量为80keV时,79 ~ 92号元素的偏差明显增加,最大偏差达328.5%。
|
图 8 各能量点的公式(9)计算值与NIST提供的相应值曲线 |
|
图 9 各能量点公式(9)计算值与NIST相应提供值比较的偏差(%)曲线 |
各个能量值,43、61、84号元素的计算值与NIST提供的相应值都出现了明显的偏离,可能这几种物质与X、γ射线相互作用有特殊的表现,也可能NIST提供的这几个元素的相应值出现了较大的偏差。
能量为100 keV时,87 ~ 92号元素的偏差明显增加,能量为80 keV时,79 ~ 92号元素的偏差明显增加,其原因可能是由于没有考虑“吸收限”的修正。100 keV以上各种元素的线性衰减系数“吸收限”的影响规律基本相同,但100 keV以下随入射X、γ射线能量的递增,各元素线性衰减系数受“吸收限”的影响不一致,需要根据能量和原子序数的递增考虑“吸收限”对计算公式的修正[7]。由于本研究涉及的能量范围内,“吸收限”的影响仅在80 keV ~ 100 keV内高原子序数部分表现,所以本研究仅提出“吸收限”的影响不对其进行修正。
由于80 keV ~ 1000 keV能量范围X、γ射线与物质相互作用主要考虑光电效应和康普顿散射,瑞利散射的影响很小,对其参数不做修正。为了保持系统的完整性,本文直接利用公式(3)中提到的瑞利散射的相关参数。
| [1] |
Hubbell JH. Review and history of photon cross section calculations[J]. Phys Med Biol, 2006, 51: 245-262. DOI:10.1088/0031-9155/51/13/R15 |
| [2] |
Seltzer SM. Calculation of Photon Mass Energy-Transfer and Mass Energy-Absorption Coefficients[J]. Rad Res, 1993, 136: 147-170. DOI:10.2307/3578607 |
| [3] |
Seltzer SM, Hubbell JH. Tables and Graphs of Photon Mass Attenuation Coefficient and Mass Energy-Absorption Coefficients for Photon Energies 1 keV to 20 MeV for Elements Z = 1 to 92 and Some Dosimetric Materials. Appendix to invited plenary lecture by Hubbell JH"45 Years (1950-1995) with X-Ray Interactions and Applications"presented at the 51st National Meeting of the Japanese Society of Radiological Technology[P]. Nagoya, 1995: 14-16.
|
| [4] |
Storm E, Israel HI. Photon Cross Sections from 1 keV to 100 MeV for Elements Z = 1 to Z = 100[J]. Nucl Data Tables A, 1970, 7: 565-681. DOI:10.1016/S0092-640X(70)80017-1 |
| [5] |
CHEN Min-cong, LI Hong-mei, CHEN Zi-yu, et al. An examination of mass thickness measurements with X-ray sources[J]. Applied Radiation and Isotopes, 2008, 66: 1387-1391. DOI:10.1016/j.apradiso.2008.04.012 |
| [6] |
高上凯. 医学成像系统[M]. 北京: 清华大学出版社, 2000: 16-17.
|
| [7] |
Johns HE, Cunningham JR. The Physics of Radiology[J]. Med Phys, 1984, 11(5): 731-732. |