2. 军事医学科学院放射与辐射医学研究所
2. Institute of Radiation Medicine, Academy of Military Medical Sciences
氡及其子体是诱发肺癌的第二位致肺癌的病因。据世界各国的统计资料, 人类肺癌的10%左右归因于氡及其子体的吸入照射。氡是世界卫生组织(WHO)公布的19种环境致癌物之一[1]。国际癌症机构(IARC)也将氡及其子体列为一类致癌因素[2]。在我国, 估计约有15%的肺癌是由氡暴露引起的, 每年因氡暴露所致肺癌死亡可达10万人左右。
依据多家国际学术权威机构发布的资料, 1996年以来在国内发布的有关放射性肿瘤判断的3份标准[3-5]均将氡致肺癌列为可以估算其辐射病因概率的放射性肿瘤之一。2013年启动的对现行的GBZ 97- 2009的修订方案仍然如此。
超额相对危险(ERR)是氡致肺癌病因判断中的一个重要参数。为此, 笔者曾于2012年发表一文[6]系统地介绍了1984-2003年间国际上与氡致肺癌ERR相关的一些资料, 尤其是美国国立卫生研究院(NIH) 2003年的一份报告(NIH 03-5387)[7]。根据修订GBZ 97-2009工作组的总体要求, 本文就应用NIH 03 -5387中氡致肺癌部分的背景资料作一介绍。
1 NIH 03-5387模型简介在NIH 03-5387报告中, ERR是氡暴露量(wlm)、诊断时年龄(a)、最后一次暴露后经历时间(t)的函数[7]:
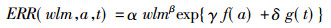
|
(1) |
式中, α、β、γ、δ是未知参数, 可以通过实际观测数据估计得到; f(a)和g(t)分别为:
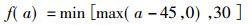
|
(2) |
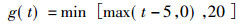
|
(3) |
由式(1)可以看出, ERR依赖于a(岁)和t(年数), 不同的a或者t, 相应的ERR是不相同的。对于单位暴露量, 也就是1个工作水平月, ERR可被表示为:
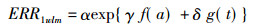
|
(4) |
在以往的其他模型中, ERR1wlm被设定为常数, 或者是几个相互独立的因子之积, 只有一个单一的点估计值。而在NIH 03-5387模型中, 为了说明不同来源的不确定性, 假定ERR1wlm服从对数正态分布。在NIN 03-5387表Ⅳ.D.10中, 给出了a≤45、a=63、a≥75, t≤5、t=15、t≥25时, 从0.0025~0.9975分位点的ERR1wlm。具体计算时, 任意暴露量wlm的ERR等于wlm0.82与ERR1wlm之积, 即ERR=wlm0.82 × ERR1wlm, 这里的0.82实际上就是式(1)中参数β的取值。
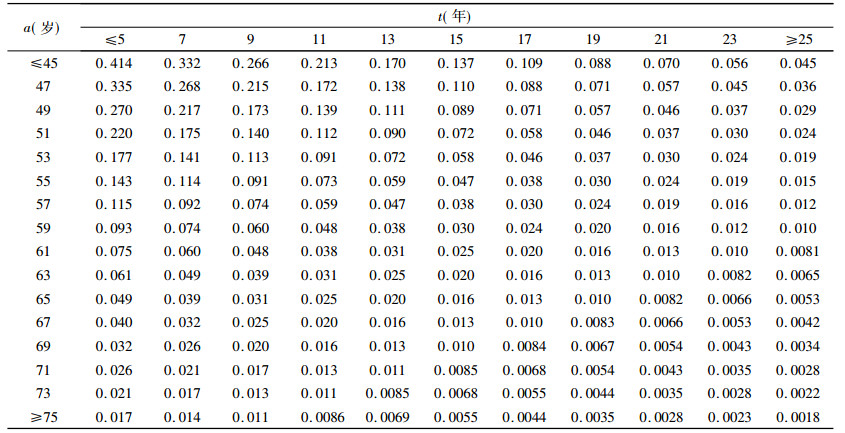
2 不同情况下ERR1wlm的计算NIN 03-5387[7]表Ⅳ.D.10中仅给出了有限的a和t所对应的ERR1wlm, 为了满足实际应用的需要, 还需给出逐年的依赖于a和t的ERR1wlm值。在笔者2012年文[6]中, 采用了对数线性内插法, 计算了a在45~75岁之间, t在5~25年之间, 逐年的吸烟者与未吸烟者的0.50和0.99分位点的ERR1wlm。除此之外, 还给出了不同情况下未吸烟者与吸烟者、0.95与0.50分位点ERR1wlm的比值。
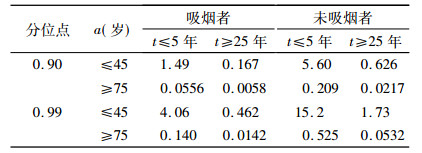
NIN 03-5387表Ⅳ.D.10给出了多个分位点的ERR1wlm, 但是仍有一些在病因判断上重要分位点对应的ERR1wlm未给出, 例如0.90与0.99分位点。在本文的计算中, 根据已有的分位点的数据, 采用三次样条插值法(cubic spline interpolation)得到了0.90与0.99分位点的ERR1wlm[8], 见表 1, 其他重要的分位点数据可按照相同的方法计算。
|
|
表 1 a≤45或a≥75, t≤5或t≥25时0.90与0.99分位点的ERR1wlm |
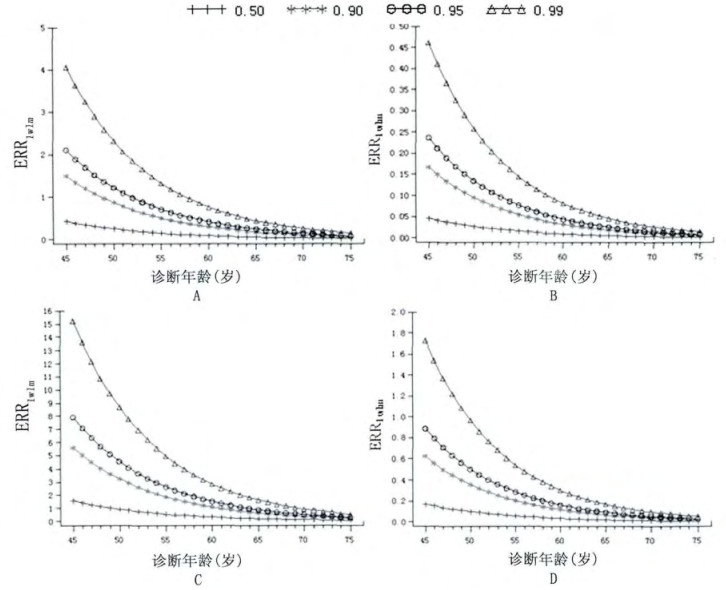
综合使用三次样条插值法和对数线性内插法, 便可得到任意分位点上所有a和t对应的ERR1wlm值, 其中t=5或t=25时, 吸烟者与未吸烟者各诊断年龄的0.50、0.90、0.95、0.99分位点的ERR1wlm见图 1。
|
图 1 不同诊断年龄时0.50、0.90、0.95、0.99分位点的ERR1wlm 注:A吸烟者, t=5;B吸烟者, t=25;C未吸烟者, t=5;D未吸烟者, t=25 |
由于ERR1wlm被假定为服从对数正态分布, 该分布的位置与形状会随着其参数(均数、标准差)取值的变化而变化, 呈现出正偏态分布或大体上的对称分布[9]。按照修订GBZ 97-2009工作组的方案, 取0.50分位点的ERR1wlm而计算得的病因概率(PC)作为判定是否为放射性肿瘤的依据。限于篇幅, 仅在表 2中仅给出吸烟者0.50分位点的部分ERR1wlm值。
|
|
表 2 吸烟者0.50分位点的ERR1wlm |
在NIH 03-5387模型中, 对潜伏期的校正采用S形函数, 其表达式为[10-11]:
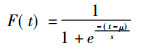
|
(5) |
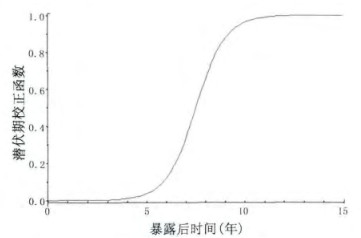
式中, t为自变量, 也就是暴露后经历时间; 对于实体癌而言, μ的取值为7.5, 它等于函数拐点处自变量t的取值, 此时函数值为0.5;在t=4年和11年时, 函数取值分别为0.01和0.99, 由此可算得S的取值为0.76168。可绘得该函数图形为:
|
图 2 氡致肺癌潜伏期函数曲线 |
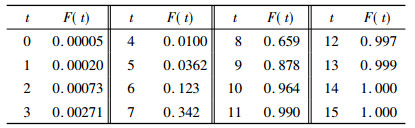
t=0~15年间各段时间的校正系数F(t)列于表 3。此处, t=0是指暴露当年。
|
|
表 3 氡致肺癌潜伏期校正系数 |
在考虑潜伏期校正的基础上, 特定wlm、a和t所对应的ERR可由下式算得:
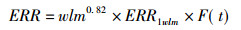
|
(6) |
式中, ERR1wlm和F(t)可分别由表 2和表 3查得。
3.2 吸烟校正在放射性肺癌的病因判断中, 要考虑辐射致癌与吸烟的相互作用, 根据吸烟情况对ERR进行校正和调整。对于一般的肺癌(除氡致肺癌以外), 吸烟情况被分为三种类别:①从未吸烟者; ②曾经吸烟者; ③目前吸烟者。其中目前吸烟者又进一步被划分为四个等级:(1) < 10支/d; (2)10~20支/d; (3)21~40支/d; (4)> 40支/d。不同的吸烟类别分别采用不同的校正系数对ERR进行调整[4]。在对GBZ 97-2002的修订中, 对于氡致肺癌, 吸烟情况分为吸烟者与未吸烟者两类, 其中未吸烟者的ERR是吸烟者的3.8倍[6, 10]。因此, 将表 2中的数据乘以校正系数3.8, 就能够得到未吸烟者的ERR1wlm, 进而可以算得未吸烟者的ERR, 其表达式如下:
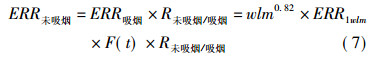
|
(7) |
式中,R未吸烟/吸烟代表吸烟校正系数3.8。
3.3 多次照射和多年照射时ERR的计算当某一职业暴露者经历过多次照射并且所有照射发生在同一年时, 可累计多次照射的暴露量计算得最终的ERR。当某一职业暴露者多次照射发生在不同年份, 需要逐年计算每年的ERR, 然后将所有年份的ERR进行累加, 作为最终的ERR。
4 应用举例根据上文中的讨论, 可以将NIN 03-5387模型[7]用于氡职业暴露者病因概率的计算, 以下将GBZ 97-2009[5]附录E例3作为举例计算。
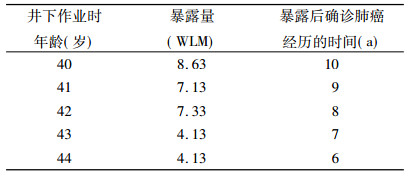
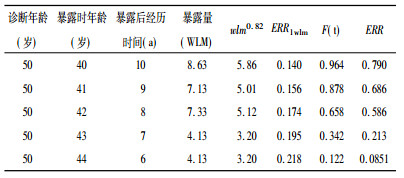
例:男性, 40~44岁间从事铀矿井下作业5年, 历年暴露量(包括井下γ照射折算的暴露量)见表 4, 50岁时被诊断患肺癌, 该例吸烟情况为10~20支/d。
|
|
表 4 某患肺癌者铀矿井下作业5年氡暴露量 |
(1) 根据GBZ 97-2009附录B的计算方法, 算得的ERR和PC分别为:
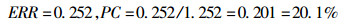
|
(2) 根据本文中的计算方法, 应用NIN 03-5387模型, 逐年计算ERR然后累加:第一步, 根据表 2, 可查得诊断年龄(a=50)、暴露后经历时间(t=6~10)的有吸烟史的ERR1wlm; 第二步, 根据式(6), 结合表 3中的潜伏期校正系数, 可计算得到各年的ERR; 第三步, 将各年ERR合计, 得到总的ERR, 计算病因概率PC。
上述过程计算结果列于表 5。由此表, 合计的ERR为2.36, 相应的PC为70.2%。
|
|
表 5 表 4举例计算的ERR和PC |
将以上信息录入美国国立癌症研究所(NCI)的交互式放射流行病学程序(IREP)[12]所在的网页, 对本文计算结果进行验证, 该程序计算的PC值为71.4%, 两者吻合佳。
因此, 本文上述内容已写入GBZ 97-2002修订版本的核心内容。
5 讨论NIH 03-5387模型拥有一系列优点, 包括方法体系完整, 数据可利用性强, 发表年份近等, 它的最大特点在于, 通过假定ERR服从特定的概率分布来说明不同来源的不确定性。在IREP中, 除了对数正态分布以外, 使用者还可以选择正态分布、三角分布、对数三角分布、均匀分布、对数均匀分布作为不确定性的分布类型[12], 而在本文中, 仅选择对数正态分布进行研究和探讨。此外, 对于暴露量, 也可以假定其服从上述概率分布或者是常数, 本文中的计算将暴露量设定为常数。对于不同分布类型的研究和比较, 将是我们下一步要做的工作。
需要指出的是, NIH 03-5387模型本身也存在一些不足和局限性, 例如, 氡致肺癌的ERR是仅仅根据男性的数据估计得到的, 它被直接应用于女性, 实际上女性的ERR可能高于男性; 肿瘤的基线风险会随着时间改变, 如果不考虑这种改变, ERR可能会被低估或高估; 潜伏期校正函数的确定带有一定的主观性[12]。尽管如此, 这些不足并不妨碍NIH 03-5387模型在实际应用中的合理性。目前来讲, 它仍然是最科学和最先进的方法之一。
| [1] |
International Programme on Chemical Safety, Environmental Health Critreia 211. Health Effects of Interactions between Tobecoo Use and Exposure to Other Agents[M]. Genewa: World Health Organization (WHO), 1999: 57-59.
|
| [2] |
International Agency for Research on Cancer. IARC Monographs on Evaluation of Carcinogenic Risk to Humans:Fiberes and Radon[M]. Lyon: IARC, 1988.
|
| [3] |
中华人民共和国卫生部.GB 16386-1996放射性肿瘤判断标准及处理原则[S].北京: 中国标准出版社, 1996.
|
| [4] |
中华人民共和国卫生部.GBZ 97-2002放射性肿瘤诊断标准[S].北京: 中国标准出版社, 2002.
|
| [5] |
中华人民共和国卫生部.GBZ 97-2009放射性肿瘤病因判断标准[S].北京: 中国标准出版社, 2009.
|
| [6] |
叶常青, 柳伟伟, 胡良平, 等. 对氡致肺癌病因判断若干问题的探讨[J]. 中华放射医学与防护杂志, 2012, 32(3): 318-322. DOI:10.3760/cma.j.issn.0254-5098.2012.03.025 |
| [7] |
National Institutes of Health.Report of the NCI-CDC Working Group to Revise the 1985 NIH Radioepidemiologcal Tables[R].NIH Publication No.03-5387.Washington DC: US Department of Health and Human Services/National Institutes of Health/National Cancer Institute, 2003.
|
| [8] |
邢丽. 三次样条插值端点约束条件的构造与MATLAB实现[J]. 上海第二工业大学学报, 2012, 29(4): 319-323. DOI:10.3969/j.issn.1001-4543.2012.04.013 |
| [9] |
方开泰, 许建伦. 统计分布[M]. 北京: 科学出版社, 1987: 9.
|
| [10] |
David C.Kocher, A.Iulian Apostoaei, Russell W.Henshaw, et al. Interactive Radioepidemiological Program (IREP):A Web-based Tool for Estimating Probability of Causation/Assigned Share of Radiogenic Cancers[J]. Health Physics, 2008, 95(1): 119-147. DOI:10.1097/01.HP.0000291191.49583.f7 |
| [11] |
de Gonzalez Amy Berrington, Apostoaei A Iulian, Veiga Lene H S, et al. RadRAT:A Radiation Risk Assessment Tool for Lifetime Cancer Risk Projection[J]. J Radiol Prot, 2012, 32: 205-222. DOI:10.1088/0952-4746/32/3/205 |
| [12] |
National Cancer Institute.The Interactive RadioEpidemiological Program (IREP)[Z].https://www.irep.nci.nih.gov/irep,2011,12.
|