2. 四川大学华西公共卫生学院;
3. 成都市疾病预防控制中心
2. West China School of Public Health, Sichuan University;
3. Chengdu Center for Disease Control and Prevention
四川省是核技术应用大省, 大多数核设施建于20世纪60年代, 设备老化、技术落后, 部分设施周边人口稠密、交通不便, 一旦发生核事故, 医学应急人力资源的有效调配将对核应急救援的效率和成败起着关键作用。因此, 有效合理配置四川省医疗卫生技术人员资源以利于发生核事故时有效调配医疗卫生技术人员, 保证核应急救援工作的顺利开展。医疗卫生资源指医疗卫生系统所拥有和使用的人、财、物、技术和信息等各种要素的总和, 是卫生服务活动中生产和再生产的物质基础。而卫生技术人员是一个国家或地区医疗卫生系统的重要组成部分, 世界卫生组织报告指出卫生技术人员包括医师、护士、药剂人员、检验人员、影像人员以及其他具有高等教育程度的技术人员[1], 对卫生技术人员的分析及预测可有利于卫生人力资源的有效合理配置, 也可促进整体医疗事业的发展。本研究通过收集四川省医疗卫生系统1995-2013年卫生技术人员数, 采用ARIMA模型对四川省1995-2013医疗卫生技术人员数进行分析并对2014-2020年的卫生技术人员需求量进行预测, 从而为四川省核应急医疗卫生人力资源的有效合理调配提供参考依据。
1 资料与方法 1.1 资料来源四川省医疗卫生系统1995-2013年卫生技术人员数来源于四川省卫生统计年鉴(2012)、四川卫生年鉴(2013)、四川省统计局统计公报, 数据真实可靠。
1.2 方法 1.2.1 ARIMA模型的基本原理ARIMA模型, 即差分自回归移动平均模型(Autoregressive Integrated Moving Average Model, 简称ARIMA)是Box-Jenkins方法中重要的一种预测模型, 适用于处理非平稳时间序列, 其基本思想是将时间序列视为一组依赖于时间(t)的随机变量, 它综合考虑了序列的趋势变化、周期变化及随机干扰, 并借助模型参数进行了量化表达, 用相应模型描述出来, 即可用过去和现在的观察值来预测未来值。ARIMA模型简记为ARIMA (p, d, q), 其中p为自回归项, q为移动平均项数, d为时间序列成为平稳序列所需要的差分次数[2-3]。
1.2.2 ARIMA模型的构建采用Eviews 3.1统计软件构建ARIMA模型并进行参数估计; 采用SPSS 18.0统计软件对2014-2020年四川省医疗卫生技术人员数进行预测。ARIMA模型的构建分为以下四步[3-4]: ①数据的平稳性处理:对原始数据平稳性检验一般采用ADF单位根检验以及序列图进行辅助观察, 对序列的平稳性进行检验。②模型的识别和定阶:序列平稳后, 通过观察ACF和PACF图对目标序列进行模型初步的识别和定阶。③参数估计及模型检验:在初步模型识别的基础上, 计算模型参数, 并进行显著性检验和残差的白噪声检验, 若残差为白噪声序列, 表示所建立的模型适合用于预测, 拟合优度好。④预测:根据所建立的ARIMA模型对将来某个时段的卫生技术人员数及可信区间进行预测。
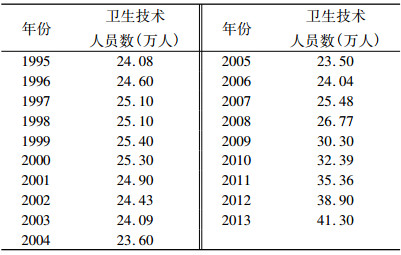
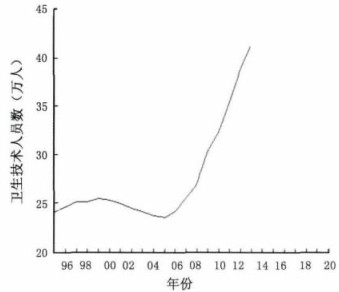
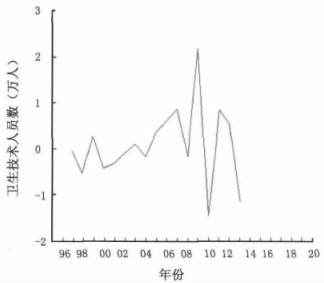
2 结果 2.1 数据平稳化处理及模型识别依据四川省1995 -2013年医疗卫生技术人员资料(表 1)作时序图。从四川省医疗卫生技术人员数序列图(图 1)可知, 1995-2013年四川省卫生技术人员数有较明显的上升趋势, 序列可能不平稳; 同时对原始序列作单位根检验发现单位根检验统计量t为-1.0772, 而在5%的显著性水平下单位根检验统计量t为-1.9658, 上述统计量大于5%显著性水平下的临界值, 说明原始序列存在单位根, 为非平稳序列, 暂不能用ARIMA模型直接建模。对原序列进行差分转换, 经过分析检验可知原序列在二阶差分后趋于平稳, 即d=2 (图 2)。
|
|
表 1 四川省1995-2013年医疗卫生技术人员数基本情况 |
|
图 1 四川省医疗卫生技术人员数时序图 |
|
图 2 医疗卫生技术人员二阶差分时序图 |
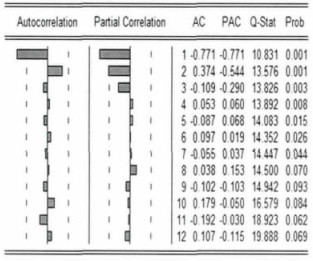
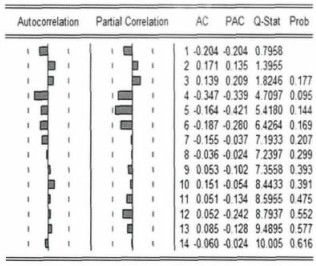
根据二阶差分后的自相关函数ACF图和偏相关函数PACF图(图 3), 可知差分后平稳序列的偏相关函数和自相关函数均是拖尾的, 因此序列适合ARIMA (p, d, q)模型。经过由低阶到高阶的尝试, 对ARIMA模型的参数进行估计, 选出最优的3个参数为d=2, p=1, q=1。此时, 对平稳序列作单位根检验发现统计量t为-8.7726, 而在5%的显著性水平下单位根检验统计量t为-3.8288, 上述统计量小于5%显著性水平下的临界值, 拒绝原假设, 说明序列不存在单位根; 再由图 4、图 5可知也说明序列为白噪声序列, 提取信息充分, 可以建立ARIMA (1, 2, 1)模型。
|
图 3 二阶差分后的自相关和偏相关图 |
|
图 4 残差项序列自相关和偏相关图 |
|
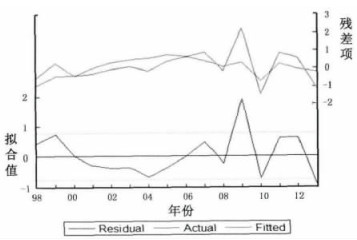
图 5 拟合值及残差图 |
对残差项作单位根检验发现统计量t为-8.1022, 而在5%的显著性水平下单位根检验统计量t为-3.8730, 上述统计量小于5%显著性水平下的临界值, 拒绝原假设, 模型残差经过白噪声检验。同时, 模型检验得到拟合统计量R2=0.9699, 可认为拟合的模型是较优的。
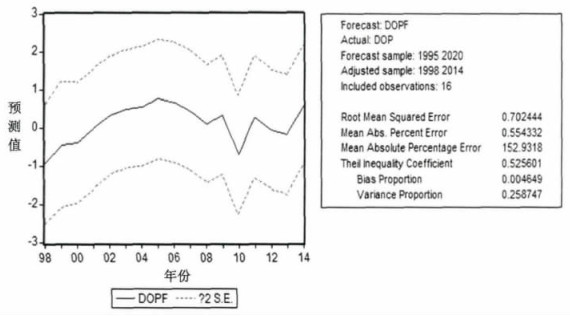
由图 6可知, Static预测方式显示的预测值波动较大, Theil不相等系数为0.5256, 表示模型预测能力较好; 方差比例较小(0.2587), 说明较好的模拟了实际序列的波动。综合来说, 模型的预测效果较理想, 可以采用ARIMA (1, 2, 1)模型进行预测。
|
图 6 Static预测方式结果 |
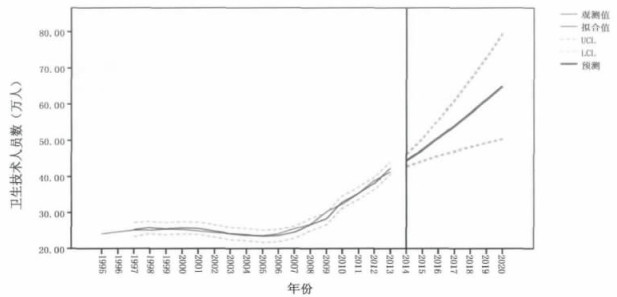
从图 7可以看出, 四川省1995- 2013年医疗卫生技术人员实际人数与ARIMA模型预测人数相差不大, 拟合效果较好, 预测结果可信, 可以进行下一步预测分析。
|
图 7 四川省1995~2013年医疗卫生技术人员实际值与预测值 |
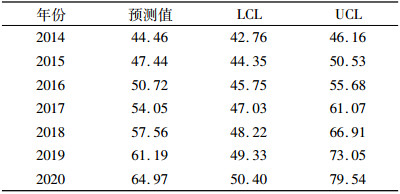
从2014-2020年四川省医疗卫生技术人员预测值来看, 四川省的医疗卫生技术人员呈平稳的上升趋势, 2014年医疗卫生技术人员预测值为44.46万人, 到2020年将增至64.97万人(表 2)。
|
|
表 2 四川省2014~2020年医疗卫生技术人员预测值(万人) |
四川省是人口大省及核技术应用大省, 医疗卫生资源需求量大; 再加上医疗卫生人力资源的有效调配将对核应急救援工作起着关键作用, 因此适度增加医疗卫生技术人员是有必要的。而研究发现, 四川省各级医疗卫生机构的卫生技术人员结构不合理[5], 护理等部分技术人员出现严重的缺口; 同时卫生技术人员质量不高、分布不合理。这些将导致医疗卫生人力资源的利用率低, 并会阻碍到整个医疗事业的发展及核应急医学人力资源的调配工作。对于卫生技术人员的总量增长来说, 并不是越多越好, 而是应当控制发展, 以达到供需平衡。因此, 为科学合理的规划医疗卫生技术人员资源, 本研究采用ARIMA (1, 2, 1)的时间序列分析方法对四川省医疗卫生技术人员进行分析预测。通过对ARIMA (1, 2, 1)模型残差项作单位根检验、自相关函数图及偏相关函数图、预测效果检验等, 结果显示ARIMA模型适用于卫生技术人员的预测, 且精度较高、结果可信。
本研究结合分析预测结果以及四川省医疗卫生人力资源的实际情况, 对未来医疗卫生机构针对卫生技术人员的培养及发展提出以下举措:
首先, 应注意加大对卫生技术人员的培养与引进力度。从ARIMA (1, 2, 1)模型的预测值可以得出, 2013年到2020年四川省医疗卫生技术人员的需求数量将会有23.67万人的缺口, 如何合理培养与引进卫生技术人员, 保证供需平衡, 是目前医疗卫生机构发展卫生事业的重中之重。因此, 一方面, 政府应适当增加对医疗卫生机构、高等医学院校等培养卫生技术人员的费用, 完善公益性财政补偿机制, 支持医疗机构、医学院校等对相关技术人员的培养及引进。另一方面, 医疗机构自身应注重卫生技术人员的结构化管理, 重视均衡发展, 提高各专业技术人员的业务水平。
其次, 培养全科医学人才, 开展多层次、多渠道、全方位的继续教育形式:四川省医疗卫生机构在引进专业技术人员的同时不仅仅要考虑数量上的充足, 同时也要看重人员的专业素质。政府应加大对全科医学人才的培养, 保证医疗卫生技术人员在专业上有全面的发展, 同时也可缩减部分不必要的人力资源。此外, 四川省医疗卫生机构应注重对各层次卫生技术人员的继续再教育, 可以组织卫生技术人员自学、临床病例讨论、外出进修、参加学术会议等形式增加相关人员学习交流的机会。同时也可以采取资源共享的方式促进人与人、机构与机构、上级与下级机构之间的沟通学习, 比如上一级医疗机构通过派遣高能力的卫生技术人员到下一级医疗机构进行业务指导; 而下一级医疗机构通过组织相关卫生技术人员到上一级医疗机构进行学习交流; 以这样的方式既可以增强卫生技术人员之间的学习交流机会、提高医疗卫生技术人员的业务水平, 同时也可以整合部分医疗卫生人力资源, 从而达到资源共享。
同时, 医疗卫生机构可建立针对卫生技术人员的激励机制:医疗卫生机构引进卫生技术人员后如何避免人才流失也是目前医疗事业单位考虑的重要问题。Katrina等人[6]对尼泊尔农村地区的全科医师(卫生技术人员范畴)的定性研究发现, 影响其继续留任的重要因素包括经济激励和非经济激励两大方面:职业发展(晋升机会)、获得认可、经济激励、工作条件、子女教育、继续医学教育等。因此, 四川省医疗卫生机构在培养或引进卫生技术人员的同时也要建立完善的激励机制, 从而留住人才并有效合理的规划卫生技术人力资源。
| [1] |
Anand S, 范玉华, 张俊华, 等. 中国卫生人力资源:数量, 质量和分布[J]. 21世纪中国与全球健康, 2008, 10(2): 260-269. |
| [2] |
博克斯. 时间序列分析-预测与控制[M]. 北京: 中国统计出版社, 1997: 101-149.
|
| [3] |
余华丽, 常晓松, 赵莹, 等. 利用ARIMA模型对2007~2011年四川口岸出境人员中HBsAg阳性疫情分析和预测[J]. 中国国境卫生检疫杂志, 2013, 36(1): 1-4. |
| [4] |
王燕. 应用时间序列分析[M]. 北京: 中国人民大学出版社, 2008.
|
| [5] |
冯超, 李建, 林发忠, 等. 四川省医疗机构卫生人力资源现状分析[J]. 现代预防医学, 2009, 36(8): 1 474-1 476. |
| [6] |
Katrina B, Brace H, Bhusan N. Retention of general practitioners in rural Nepal:A qualitative study[J]. Aust.J.Rural Health, 2008, 16: 201-206. DOI:10.1111/ajr.2008.16.issue-4 |