随着社会进步与经济的快速发展, 城市规模的不断扩大, 电力需求快速增长, 输变电项目迅猛增加, 但电网的快速发展, 各种变电设备、变电站以及输电线路必不可少的会经过居民区, 由于在输变电工程电磁环境影响方面缺乏有效的知识普及和正确的引导, 导致由输变电工程电磁环境所引发的纠纷问题越来越突出, 居民过度维权造成电网建设受阻, 不仅影响了国民经济的发展, 更严重影响了城市居民用电的保障[1]。
输电线路是电力系统的重要组成部分, 研究输电线路周围电磁场的分布, 了解输电线路不同相序布局下空间电磁环境的区别, 对认识输变电系统的环境影响, 指导输变电工程的电磁环境评估具有重要的意义。本文选取某220 kV典型同塔双回输电线路为例进行分析。
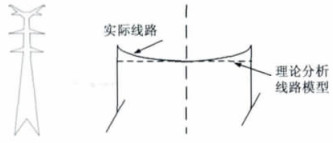
1 输电线路电磁场的计算与评估标准高压输电线路的输送距离比较长, 为简化计算, 可忽略端部效应和弧垂, 将线路视为无限长直平行导线。取实际线路弧垂最低点为导线的离地高度, 高压架空输电线可以近似看成平行于地面的多根圆柱导体。不同相的输电线带有不同的对地电压。线路电流可认为三相对称正弦稳态电流, 忽略避雷线的影响等。研究地面附近电场的分布情况时, 避雷线(即架空地线)对电磁场分布的影响很小, 为了简化计算模型, 所建立的计算模型都可以忽略避雷线的影响。由于大地的磁导率与空气相差很小, 因此将大地和空气作为同一种介质对待, 取磁导率为真空磁导率。综上所述, 实际输电线路可简化为图 1所示的理论计算模型。
|
图 1 实际和理论计算架空线路图 |
采用等效电荷法对输电线路工频电场强度和磁感应强度的分布建立数学模型, 等效电荷法以静电场的镜像法为基础, 是"国际大电网会议36.01工作组推荐的方法。
1.1 电场强度计算空间任意一点的电场强度可根据叠加原理计算得出, 在(x, y)点的电场强度分量Ex和Ey可表示为:
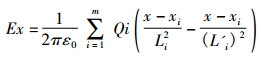
|
(1) |
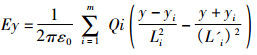
|
(2) |
式中:xi、yi——导线i的坐标(i=1、2、… m); m——导线数目; ε0——空气的介电常数; Li——各导线间的距离; L'i——各导线与其镜象导线间的距离。
1.2 磁场强度计算磁场的精确计算需要考虑的因素比较复杂, 需要考虑杆塔形状、大地的不良导电反应等, 一般情况下为了简化分析, 根据叠加理论可以直接计算出三相对称电流在空间某一点的磁感应强度值, 设三相对称电流为IA, IB, IC, 则空间H点的磁感应强度为:
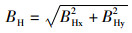
|
(3) |
其中BHx和BHy为H点的磁感应强度的水平和垂直分量, 具体可按式(4)、(5)来计算:

|
(4) |
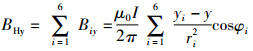
|
(5) |
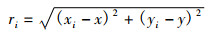
|
(6) |
其中, xi, yi为导线的横坐标和纵坐标, x, y为空间H点的横坐标, r为H点距离导线的距离。
1.3 评估标准对于超高压送变电设施的工频电场、磁场强度限制目前尚无国家标准。一般以《500 kV超高压送变电工程电磁辐射环境影响评价技术规范》(HJ/T 24-1998)(下称《规范》)中的规定进行评估, 即以4 kV/m作为居民区工频电场评价标准, 0.1 mT作为磁感应强度的评价标准。此外, 《规范》规定送电线路的测量是以档距中央导线弧垂最大处线路走廊中心为原点, 沿垂直于线路方向进行, 测点间距为5 m, 顺序测至边相导线地面投影点外50 m处止。分别测量离地1.5 m处电场强度垂直分量、磁场强度垂直分量和水平分量"[2]。
2 理论计算与分析根据《国家电网公司输变电工程典型设计》可知, 220 kV双回架空输电线路直线塔呼高一般为33~ 45 m, 本文中选用典型直线塔2E2-SZ3, 塔型结构参数:呼高33 m, 上层两线路间距10.0 m, 中层间距12.0 m, 下层间距11.0 m, 上层与中层垂直间隔6.8 m, 中层与下层垂直间距6.4 m。导线型号为LGJ- 400/35钢芯铝绞线, 双分裂, 导线直径26.82 mm, 最大负荷电流460 A。
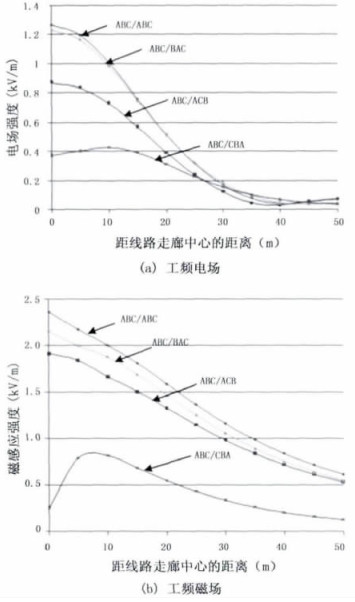
考虑弧垂, 导线架设对地高度一般为18~27 m之间。通过上述等效电荷法, 计算导线对地高度为25 m时, 四种相序(ABC/ABC、ABC/BAC、ABC/ACB、ABC/CBA)排列方式下垂直线路方向为0~50 m, 地面1.5 m处的工频电磁场。结果如图 2所示。
|
图 2 四种相序排列方式下工频电磁场理论计算结果 |
比较图 2所示的四种输电线路不同相序排列方式的计算结果可知, 距线路走廊中心投影两侧20 m区域内, 按ABC/ABC及ABC/BAC相序排列, 距地面1.5 m处的工频电场明显较大, 按ABC/CBA相序排列的工频电场强度最小; 同时还可以发现在线路走廊中心投影两侧30 m以外, 工频电场已经很小, 远低于限值, 且具有较小的波动范围。图 2(b)给出了不同相序排列方式下的工频磁场的分析结果, 从图 2(b)可知四种相序排列方式下的工频磁感应强度都远小于限值且相差不大, 因此, 工频电磁场对周围环境影响, 主要需重点关注工频电场的限值问题, 下面主要通过电磁仿真软件研究线路下方工频电场的分布情况及其对人体的影响。
3 仿真分析电磁场的求解采用有限元法进行求解计算, 其基本思想是把连续的求解域划分为有限个网格单元, 在每个单元内选取一些合适的点作为求解函数的插值点, 将微分方程(组)改写成由各变量或其导数的节点值与所选的插值函数组成的线性方程(组), 求解线性方程(组)获得近似解来代替求解域内的真值[3, 4]。
3.1 双回输电线路工频电场分析关于理论计算模型做一下假设:大地的电势设为0 V, 一回相序保持ABC顺序不变, 改变另一回相序可得到的如图 3所示的仿真结果。图 3所示的工频电场分布图种, 四条工频电场等值线由外往里分别为1 kV/m、2 kV/m、3 kV/m、4 kV/m, 而中间白色区域为工频电场强度大于10 kV/m。

|
图 3 四种相序排列方式下工频电场分布图 |
从图 3所示的结果中可以看出:①工频电场强度E≥4 kV/m的区域集中在对地高度25 m以上, 即净空高度满足≥8 m时, 线路下方的工频电磁场即可满足标准限值要求; ②当采用ABC/CBA相序排列, 距离地面高度≤14.7 m时, 线路走廊中心两侧50 m区域内的工频电场强度E≤1 kV/m; 当采用ABC/ACB相序排列, 距离地面高度≤7.4 m时, 线路走廊中心两侧50 m区域内的工频电场强度E ≤1 kV/m; 而采用ABC/ABC、ABC/BAC两种相序排列, 线路走廊中心两侧50 m范围内存在工频电场强度E≥1 kV/m的区域; ③一般在高压线路下, 人员可达的区域在距离地面2 m的范围内, 通过对比分析四种不同相序排列方式下空间工频电场仿真结果可知, 当同塔双回输电线路采用ABC/ABC和ABC/BAC的相序排列时, 人员活动区域的电场强度明显大于采用ABC/CBA相序排列时的电场强度。
3.2 输电线路下人体内外的电场分布按照人体的轮廓形状建立人体和输电线路仿真模型, 经验可知人体的相对介电常数分布不均且和频率关系密切, 50 Hz下人体内活组织的相对介电常数范围是105~2 × 106[5]。本文假定人体由均匀介质构成, 其电导率为0.1 S/m, 相对介电常数为106。下面选取线路下方电场强度较大的ABC/ABC和电场强度最小的ABC/ CBA两种排列方式, 仿真分析位于线下的人体周围电场分布情况, 如图 4所示。

|
图 4 人体周围电场分布图 |
由图 4可知, ①在整个空间的电场分布中, 人体对电场分布存在小范围的畸变, 电场强度强的部位只要集中在人的头部、肩部、手指等部位; ②头顶是突出部位且离导线最近, 在ABC/ABC相序下畸变后最大达8.5 kV/m, 肩部达5.68 kV/m, 手指达3.34 kV/m; 在ABC/CBA相序下畸变后最大达2.85 kV/m, 肩部达1.9 kV/m, 手指达0.36 kV/m。③人体虽不是理想导体但电阻很小, 所以人体内部大部分场强也很小, 是10-6数量级, 在0.89 × 10-6V/m左右。
4 结论分析结果表明, 本文所述的220 kV输电线路四种相序排列方式中, 线路下方人员可达的区域按ABC/ABC、ABC/BAC相序排列的同塔双回线路产生的工频电磁场较大, ABC/ACB次之, ABC/CBA最小。在工频电场中, 人体头部、肩部、手指等表明凹凸部位的电场强度因畸变明显增大, 体内的电场强度和稳态感应电流很小。
| [1] |
许杨, 张小青, 杨大晟. 高压输电线路工频电磁环境[J]. 电力学报, 2007, 22(1): 9-14. DOI:10.3969/j.issn.1005-6548.2007.01.003 |
| [2] |
国家环保总局. HJ/T 24-1998 500 kV超高压送变电工程电磁辐射环境影响评价技术规范[S]. 南京: 凤凰出版社, 1998. http://www.csres.com/detail/136203.html
|
| [3] |
William B.J.Zimmerman. COMSOL Multiphysics有限元法多物理场建模与分析[M]. 北京: 人民交通出版社, 2007.
|
| [4] |
邹澎, 王芳. 高压输电线附近工频电场的数学模型[J]. 中国电力, 1994(6): 20-23. |
| [5] |
Han Yunan, Lv Yinghua. Compute extremely low-frequency electromagnetic field exposure by 3-D impedance method[J]. The Journal of China Universities of Posts and Telecommunications, 2007, 14(3): 113-116. DOI:10.1016/S1005-8885(07)60160-5 |


