目前安全检查用X射线管、医用X射线管及工业无损检测用X射线管基本都采用定向辐射X射线管,该管由阴极、阳极及真空密封外壳组成。作为X射线成像装置的核心部件,定向辐射X射线管参数及结构变化直接影响产生的X射线光谱,从而影响到整个设备的性能指标。
因定向辐射X射线管产生的X射线是从低能到高能的连续谱,目前从实验上测试受很多条件的限制,所以通常通过理论计算进行分析,其中Monte Carlo方法被认为是最精确的一种方法[1, 2]。MCNP是一个大型多功能的Monte Carlo计算软件,由美国Los Alamos实验室研制,可模拟中子-光子-电子在任何材料中的耦合输运问题,光子和电子的能量范围在1 keV - 1 000 MeV,适用面宽,已经很好地用于辐射剂量计算、物理实验模拟、辐射屏蔽防护以及核仪器设计等许多方面[3, 4]。
本研究的目的是应用MCNP软件模拟,计算不同管电压和不同靶角的X射线管在无过滤和有过滤情况下的X射线出射效率和能谱分布,分析靶角和管电压对出射效率、X射线能谱、X射线平均能量的影响规律,希望对定向辐射X射线管的研发和实际应用提供一定的参考。
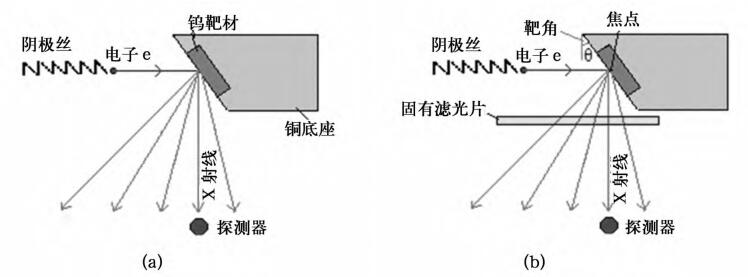
1 方法计算模型如图 1,从阴极发射的电子在电场作用下轰击靶面,与钨靶发生轫致辐射产生X射线,如图 1所示X射线从靶面反射到周围环境中。本文模拟分析了图 1(a)和图 1(b)两种结构,计算时保持接收X射线的探测器与靶面焦点距离不变,对每种结构分别计算管电压为30 kV、60 kV、90 kV、120 kV、160 kV时,不同靶角的X射线出射效率和出射能谱。同时在电压为160 kV时,考察过滤片的厚度改变对最佳靶角的影响,并分析了X射线的空间强度分布及能谱差异。
|
图 1 计算模型 |
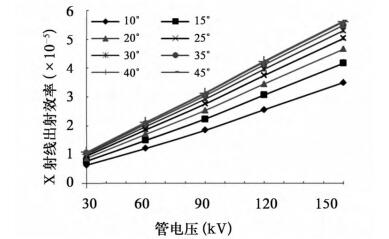
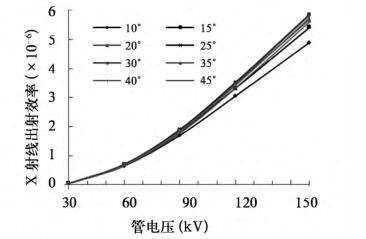
图 2和图 3分别是无过滤片和有过滤片时X射线出射效率随管电压的变化曲线。从图中可看出,对同一靶角,X射线出射效率随管电压增大而增大,无过滤片时随管电压线性增加,有过滤片时随管电压指数增加。这是因为物质对X射线的衰减过程遵循Beer-Lambert定律[5],如公式(1)所示:
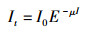
|
1) |
|
图 2 无过滤片时X射线出射效率随管电压的变化 |
|
图 3 有过滤片时X射线出射效率随管电压的变化 |
式中,It与I0分别是X射线的出射和入射强度; μ是线性衰减系数。μ的大小与X射线的能量和射线穿过的物质属性有关,X射线能量越小,μ值越大,所以在图 3中经过相同的过滤片,管电压越低,X射线被衰减掉的越多,故出射效率越低。
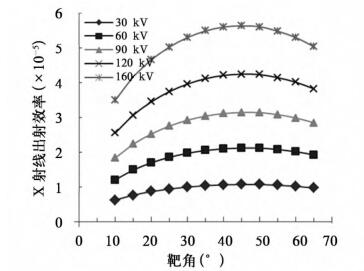
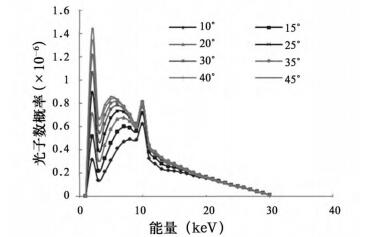
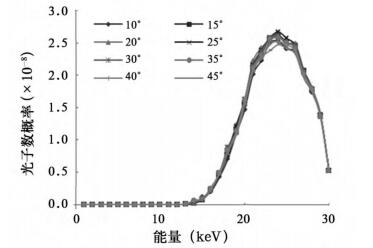
2.2 X射线出射效率随靶角的变化图 4和图 5分别是无过滤片和有过滤片时X射线出射效率随靶角的变化曲线。从图中可看出,对同一管电压,X射线出射效率随靶角增加先增大后减小,存在一个最佳靶角。表 1列出了几个管电压在无过滤片和有过滤片时的最佳靶角值。从表中可看出,在无过滤片时,最佳靶角均为46°; 在有过滤片时,最佳靶角随管电压的增大而增大。图 6和图 7是管电压为30 kV时过滤前后的X射线谱,从图 6可看出,随靶角的增大,低能X射线增加幅度比较大,分析认为:靶角越大,靶对X射线的自吸收越小,所以低能X射线就越丰富; 但随着靶角的进一步增大,有效焦斑越大,X射线出射效率(单位面积的X射线)就越小,所以在无过滤时,靶角在46°附近二者达到平衡。从图 7可看出,过滤后不同靶角的能谱基本趋于一致,且管电压越小,过滤后不同靶角的差别越小。
|
图 4 无过滤片时X射线出射效率随靶角的变化 |
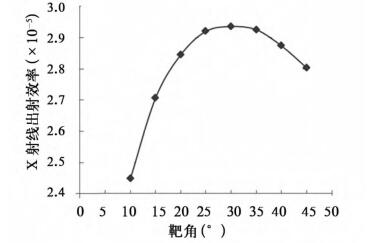
|
图 5 160kV有过滤片时X射线出射效率随靶角的变化 |
|
图 6 无过滤片时30 kV X射线管的能谱 |
|
图 7 有过滤片时30 kV X射线管的能谱 |
|
|
表 1 不同管电压下的最佳靶角 |
对同一管电压,不同的过滤片厚度会影响到最佳靶角。如表 2是管电压为160 kV时,与不同厚度过滤片对应的最佳靶角。从表中可看出,随着过滤片增厚,最佳靶角逐渐减小,但随着过滤片增厚最佳靶角的变化幅度减小。
|
|
表 2 160 kV射线管在不同厚度过滤片的最佳靶角 |
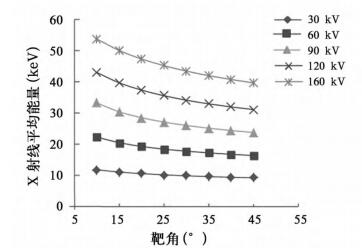
图 8和图 9是几个管电压在无过滤片和有过滤片时平均能量随靶角的变化。从两个图中可看出,平均能量均随靶角的增大而减小,随管电压的增大而增大,这是因为靶角越大,低能X射线越丰富,所以平均能量越小; 管电压越高,产生的高能X射线越多,所以平均能量越高。对比图 8和图 9可看出,有过滤片时在每个靶角的平均能量比无过滤片时小,这是因为经过过滤片后低能X射线被衰减(如图 7),即X射线被硬化。
|
图 8 无过滤片时X射线平均能量随靶角的变化 |

|
图 9 有过滤片时X射线平均能量随靶角的变化 |
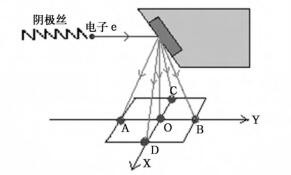
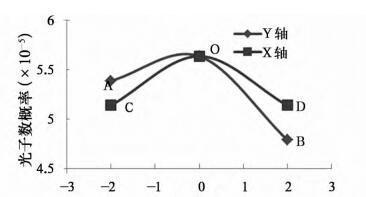
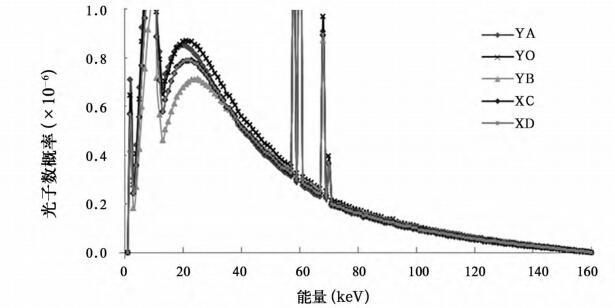
X射线在空间的强度分布对实际应用很重要,本文对30°靶角,160 kV射线管的X射线空间强度分布进行了分析。如图 10所示,分别计算了30°靶角内X轴方向和Y轴方向的A、B、C、D、O五个点的X射线强度及能谱,其中A、B、C、D点与中心O点的距离相等。从图 11的强度分布曲线可看出,X射线在X轴的强度分布是中心对称的,在Y轴的强度分布不对称,且越靠近靶面的位置强度越低。另外由于O点与焦点的距离比其他四个点小,所以O点的强度最大。这与文献[1]中提到的X射线管在轴向方向具有足跟效应相符。从图 12能谱分布可看出,A点和B点的能谱分布在40 keV以下差别比较大,C点和D点的能谱分布完全重合。为此在实际中大部分采用径向方向X射线,即X轴方向。
|
图 10 30° /160 kV X射线管强度分布计算模型 |
|
图 11 30°/160 kV X射线管无过滤片的X射线强度分布 |
|
图 12 30° /160 kV X射线管在图 10中几个位置的X射线能谱分布 |
本文应用MCNP-4C,对影响定向辐射X射线管的参数特性进行了模拟分析,计算结果表明,X射线出射效率、能谱分布和强度分布受靶角和管电压影响。X射线出射效率随管电压的增大而增大,随靶角的增大先增大后减小,存在一个最佳靶角。在无过滤片时,最佳靶角在46°附近; 有过滤片时,最佳靶角随管电压的增大而增大。对同一管电压,最佳靶角随过滤片增厚而减小; 平均能量随管电压的增大而增大,随靶角的增大而减小,无过滤片时的减小幅度比有过滤片大; X射线强度分布在轴向不对称(即图 10中Y轴方向),具有足跟效应,在径向对称(即图 10中X轴方向)。
| [1] |
杨福家. 应用核物理[M]. 长沙: 湖南教育出版社, 1994: 131-140.
|
| [2] |
Lovet X, Sorbier L, Campos CS, et al. Monte Carlo simulation of x-ray spectra generated by kilo-electron-volt electrons[J]. Appl Phys, 2003, 93: 3 844-3 851. DOI:10.1063/1.1545154 |
| [3] |
Briesmeister JF, et.al.MCNP-A General Monte Carlo N- Particle Transport Code[R]. Version 4B.1997.
|
| [4] |
许淑艳. 蒙特卡罗方法在实验核物理中的应用[M]. 北京: 原子能出版社, 1996: 20-45.
|
| [5] |
Ingle J D J, Crouch S R. Spectrochemical Analysis[M]. New Jersey: Prentice Hall, 1988.
|




