2. 中国核电工程有限公司河北分公司, 河北 石家庄 050011
在体源(即大体积放射源)的屏蔽计算中, 如果对着接受体的源面积的长、宽都不超过源与接受体间的距离时, 则可把体源近似为点源进行计算; 而当上述条件不具备时, 源介质的自吸收因素就是必须考虑的一个问题, 可以有以下两种处理方法。
1 模拟源计算方法体源计算中, 当源厚度大于平均自由程并采用点源近似计算时, 应采用一个模拟源, 其体积等于平均自由程乘以源在接受体所在平面的投影面积, 该平面垂直于接受体到源心的连线。以中放废液贮罐屏蔽计算为例, 给定条件如下:
贮罐外形尺寸为直径3 800 mm高5 000 mm, 贮罐中心与屏蔽层外表面的距离为3 m。参考源项为: 137Cs——1 × 109Bq/L; 60Co——1 × 108Bq/L。照射量率常数为:ГCs=6.312 × 10-19C·kg·m2·Bq-1·s-1; ГCo=2.503 × 10-18C·kg·m2·Bq-1·s-1[3]。源介质近似为水, 则在水中的线性减弱系数为:μCs=8.957 m -1; μCo=6.413 m-1。管理限值取Hlh=100 μSv/h, 设屏蔽介质为混凝土。
1.1 137Cs(0.662 MeV)由μCs=8.957 m-1知, 平均自由程λ=0.1116 m, 考虑源的自吸收之后, 令R为圆柱体半径, H为圆柱体高度, 则模拟源的体积为V=λ ·2R· H=2.1204 m3, 故近似源的活度为ACs= 2.1204 × 1012Bq。衰减倍数为:
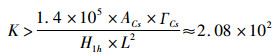
|
查表:当K=2 × 102时, 屏蔽层厚度d=49.3 cm; 当K=5 × 102时, d=55.8 cm[1]。因此49.3 cm < d < 55.8 cm。
1.2 60Co(1.25 MeV)由μCs=6.413 m-1知, 平均自由程λ=0.1559 m, 考虑源的自吸收之后, 模拟源的体积为V=2.963 m3, 近似源的活度为ACs=2.963 × 1011Bq。衰减倍数为:K≈1.154 × 102; 查表:当K= 1 × 102时, d=55.6 cm; 当K=2 × 102时, d=62.2 cm [1]。因此55.6 cm < d < 62.2 cm。
综上所述, 屏蔽层厚度可选取保守值为d=60 cm。
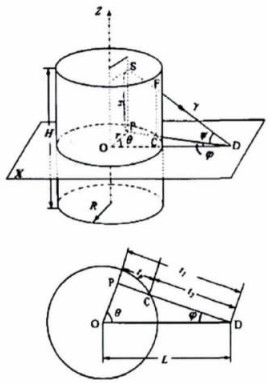
2 自吸收因子修正方法[2, 4]假定一均匀分布的圆柱型体源, 源半径为R, 源厚度即高度为H, 源介质中射线的线性减弱系数为μ, 以圆柱体中心为坐标原点, 采用圆柱坐标(如图 1所示), 考虑空间一点S(r, θ, Z), 到测量点距离为SD, 与圆柱表面交点为F, 则t=SF为射线在源介质中的自吸收距离。SD与平面夹角为ψ, 吸收距离在平面上的投影为PC, 记为tp, P点的极坐标为P(r, θ), 令PD与极轴交角为φ, 源中心点与测量点距离OD=L, 有:
|
图 1 体源模型 |
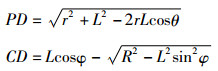
|
因此吸收距离在平面的投影为:PC=PD-CD
吸收距离t=PC·secψ
因此自吸收因子为:
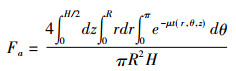
|
(1) |
由于上述积分难以计算, 故考虑在远场(L >> R, L >> H)和样品足够大(μR >> 1)条件下近似计算, 并将上式在直角坐标系内表示, 则上式变为:
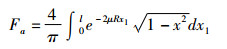
|
(2) |
在式(2)中, 如果μR >> 1, 则e-μR < < 1, 当x1→1时, 积分内的函数讯速趋于零, 则有:
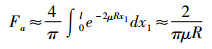
|
(3) |
该吸收因子是在满足远场条件(L >> R)和样品足够大(μR >> 1)的条件下近似得出的, 前文给定条件不满足远场条件, 但是满足样品足够大(μR >> 1)的条件, 将相关数据代入, 有如下计算结果。
2.1 137Cs(0.662 MeV)由式(3)知, 总吸收因子为:Fa≈0.0374;近似源活度为ACs=1.87 × 1012 Bq。衰减倍数为:K≈1.83 × 102。查表:当K=1 × 102时, d=44.3 cm; 当K=2 × 102时, d=49.3 cm[1]。因此44.3 cm < d < 49.3 cm。
2.2 60Co(1.25MeV)由式(3)知, 总吸收因子为: Fa≈0.05225;近似源活度为ACs=2.61 × 1011 Bq。衰减倍数为:K≈1.02 × 102。查表:当K=1 × 102时, d =55.6 cm; 当K=2 × 102时, d=62.2cm[1]。因此55.6 cm < d < 62.2 cm。
综上所述, 屏蔽层厚度可选取保守值为d=60 cm。
通过与MCNP程序计算结果进行比较, 证明由两种模拟源计算方法得到的计算结果偏大, 为保守估计。注意到两种方法的计算结果基本相同, 令单位源活度为ξ, 两种方法得到的模拟源活度为ACs1和ACs2, 则由前文知:ACs1=ξ·λ·2R·H; ACs2=2ξ·πR2·H ·(πμR)-1=ξ·H·2R·λ; 可见ACs1=ACs2, 故两种方法所得计算结果相同, 在本质上是一种方法, 同时也证明了所得到的自吸收因子公式的正确性。
| [1] |
朗J. T.著, 杨云鸿译.核燃料后处理工程[M].北京: 原子能出版社. 1980: 44-45.
|
| [2] |
吴晨彦, 田东风, 黄永义, 等. γ射线空间分布与双屏蔽圆柱形核裂变材料的几何信息[J]. 复旦学报(自然科学版), 2006, 45(4): 464-468. DOI:10.3969/j.issn.0427-7104.2006.04.009 |
| [3] |
方杰. 辐射防护导论[M]. 北京: 原子能出版社, 1991: 75-85.
|
| [4] |
陆向东.放射性核材料的特征谱分析与自吸收修正的研究[Z].中国工程物理研究院硕士学位论文, 2002: 62 -63. http://cdmd.cnki.com.cn/Article/CDMD-82818-2002114361.htm
|


