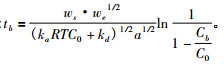在核化生突发事件的防护中, 活性炭防护面具是防护呼吸道中毒的必备物理防护器材。因此, 防护面具的研究引起国内外防护科研机构的重视。核化生防护研究从改和守两个方面展开。从防护角度, 尽可能延长防护时间, 从进攻的角度, 研究毒剂穿透防护面具的时间尽可能短。但均涉及到防护时间的实验检测和模型预测问题, 均涉及到活性炭防护面具防护时间方程。

防毒时间方程的研究是防化研究的重要领域, 是核化生防护的重要基础理论。国内外对各种改性活性碳和防毒时间模型进行了长期深入的研究和探索。建立理论上完备实践上精确实用的防毒时间方程是核化生防护的重要基础理论工作。本研究在分析文献防毒时间方程的基础上, 提出一个理论上更合理的关于核化生气溶胶粒子的新型防毒时间方程, 并进行了理论分析。

1 现有防毒时间方程及理论分析

文献中, 从经验和理论分析入手, 分别建立不同精度的防护时间方程^{[1, 2]}, 不仅能对实验数据进行回归处理, 而且有些方程能进行半经验的计算预测。比较成功防毒时间方程:

修正Wheeler equation:

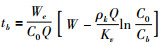
Nelson equation:

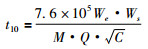
klotz. Equation:

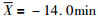
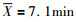
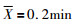
但防护时间的计算预测数值与实验数值均存在不同程度的正偏差, 如上述三种方程对112种有机物的计算预测, klotz. equationδ , Wheeler equationδ, Nelson equationδ 出现这种现象不是偶然的, 可能是由于防护时间方程简化推导过程中, 忽略了某些重要因素所致, 或对于某些因素的计算方次不合理所致, 文献解释了可能是用小分子实验测定的吸附速度常数去计算较大分子所致, 这也是可能的原因。

实验表明, 防护时间大小取决于活性炭重量、活性炭的吸附容量、洗脱速度常数、气体流量、出口、入口浓度等因素。活性炭吸附容量越大, 防护时间越长, 入口、出口浓度越大, 温度愈低, 防护时间愈短。吸附速率常数愈大, 防护时间愈长, 这点显然事实不合理。根据实验事实, 修正Wheelerequation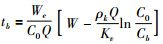中Kv与事实不一致。Wheelerequation在计算防护时间时假定了Kv是个常数, 对计算预测结果, 影响未能反映出来。不同方程分别根据一定的实验事实, 利用一定的模型假设推导出来的, 某个因素的作用是完全不同的。例如:入口浓度Co在Wheeler equation和klotz.Equation中和Nelson equation中与其入口浓度Co的中作用因子是不同的。判断哪个更合理, 需要从理论上重新认识, 并从实验上进一步验证。

2 核化生气溶胶粒子在活性炭表面上的吸附模型

核化生气溶胶粒子, 常温下蒸汽压较低, 在空气中浓度较小。在活性炭表面上的吸附基本上是单分子层的, 可以近似达到饱和吸附, 可以忽略活性炭表面上核化生气溶胶粒子间的作用。活性炭表面的均匀程度是较好的, 可近似地认为表面是均匀的。核化生气溶胶粒子在活性炭表面上的吸附是由吸附和洗脱两个同时进行的过程组成的。核化生气溶胶粒子在活性炭表面上的吸附符合Langmuir吸附模型。

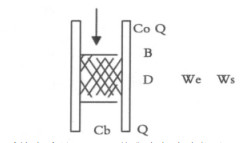
3 活性炭防护面具防护模型、防护时间方程

活性炭防护面具是个开放体系, 呼吸器官相当于一个泵, 按一定的流量呼吸一定量空气, 同时, 也又呼出一定流量的二氧化碳, 为了简化模型, 忽略人的呼吸器官对呼出的二氧化碳的影响, 假定只按照一定的流量呼吸进入和呼出活性炭防护面具。这样, 提出活性炭防护时间模型如图 1所示:

浓度为Co的毒剂以流量Q通过一定厚度的活性炭后, 经活性炭的吸附, 其出口浓度变为C_b, 显然, 开始C_b近似为零, 随后C_b逐渐地增大, 最后达到了饱和吸附C_b=C₀。

核化生气溶胶粒子浓度和分压很低, 认为核化生气溶胶粒子蒸汽符合理想气体定律, P_v=nRTt, P=cRT, 故恒温时, 可用浓度C代替压力P。设在温度为T和C₀条件下, 活性炭最大吸附容量为a_m, 假定活性炭表面单分子吸附满位, a为未达到饱和吸附前核化生气溶胶粒子在活性炭上的吸附量, t₀为出口浓度C_b≠0时的时间, 计时从核化生气溶胶粒子到达活性炭前言B开始, 出口浓度C_b为时间t的函数, 设为C(t), 时间t时,

表面覆盖度

(1)

毒剂在活性炭表面吸附模型符合Langmuiro吸附模型, k_a---吸附速率常数, k_d---脱附速率常数, 则有:

(2)

把(1)式和P₀=C₀RT代入(2)式, 整理得到:

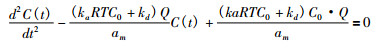
(3)

只要解出(3)式中二阶常微分方程, 即可得到C(t)函数解析表达式, 显然缺少初始条件, 从上面的活性炭防护时间模型过程分析, 不难得到

(4)

(5)

把上面(3)(4)(5)联立求解, 即可得到活性炭防护模型的数学表达式:

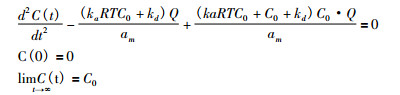
求解微分方程, 即得到C(t)函数表达式:

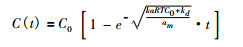
(6)

将(6)式进行变换, 得到上述活性炭防护模型的防护时间方程:

(7)

将活性炭重量为1g换算为Wsg, c(t)→t_b

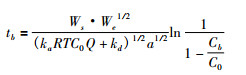
(8)

(8) 式就是从新模型得到的活性炭新型防护时间方程。

4 活性炭新型防护时间方程讨论^[3-5] 4.1 新型防护时间方程式理论分析

(1) 防护时间随活性炭重量, 吸附容量增大而增大, 随吸附速度常数k_a, 脱附速度常数k_d, 入口浓度C₀和出口浓度比值C₀/C_b, 流量Q, 温度T的增大而减少, 这些与经验事实是完全一致的。

(2) 脱附过程对防护时间的影响, 得出了脱附速度常数增大, 防护时间变短的结论, 而Wheeler、klotz、Nelsonequation都忽略了脱附过程的影响, 因而计算预测结果往往偏高, 可能与此有关, 它与吸附速度常数是相似的。

(3) 只要测定出吸附容量和洗脱速度常数k_a和k_d就可以估算活性炭的防护时间, 与Wheelerequation是一致的。

(4) 若k_d < < k_aRTC₀, 即脱附过程可以忽略的情况下, (8)式简化为

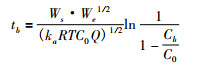
(9)

4.2 (9)式和Wheeler、klotz、Nelsonequation比较

(1) W_S与t_b成线性影响这点, 上述三个经典方程是一致的。

(2) 浓度C₀与Nelsonequation是一致的, Nelsonequation计算结果优于Wheeler和klotzequation, 可能与入口浓度C₀因次有关, 或许C₀^1/2更为合理。

(3) 流量Q, 经典三方程均为反比例关系, 而本方程则与其流量平方根成正比, 这点与浓度C₀的影响相比较是可以理解的。增加入口浓度和加大流量效果是一致的。原则上因次应该一致, Nelsonequation是不一致的, Wheeler和klotzequation是一致的。

(4) 吸附容量W_e的影响, 上述经典三方程均为正比例关系, 新型方程则为平方根正比例关系, 防护时间为吸附容量的凸函数是肯定的, 若从吸附过程的非均匀性看, 其防护时间与吸附容量非线性增加更合理。

4.3 新型防毒时间方程评价

通过理论分析, 脱附过程可以忽略的情况下, 建立的新型防毒时间方程可简化为经典的Wheeler、klotz、Nelsonequation, 经典方程是经过实践检验和应用的, 只是有些正负偏差。新型防护时间方程式理论分析, 有关影响因素浓度C₀、流量Q、吸附容量W_e、洗脱速度常数k_a和k_d理论上更合理。新型防毒时间方程是一个理论上更合理的防毒时间方程, 可望在核化生防护实践中得到广泛的应用。