中子照射事故中, 人体受照剂量的测量方法是核科学中一个重要的研究课题。笔者介绍了国内外临界事故中人体受中子照射的剂量估算方法, 重点阐述了24Na活度的测量方法。由于研究人员对辐射类型、中子源能谱、辐射入射角、人与辐射源之间屏蔽物的厚度、受照期间人体在辐射场中的取向及人体与辐射源的相对距离等影响受照剂量的因素认识不同, 修正因子的取值差异较大, 使得估算结果和实际结果相差超过50%。文章对这些因素作了描述。
测量血钠活度估算中子照射人体剂量的流程包括:第一, 测量人体中24Na的比活度, 既可以是血液样品中24Na的血样比活度, 也可以是全身24Na的人体比活度; 第二, 由比活度或活度转换为全身剂量; 第三, 对影响估算结果的因素赋予相应的权重因子, 对估算结果进行校正。这些步骤的每一步都有其不确定性, 并会导致估算结果产生误差。
1 24Na比活度的测量方法24Na的放射性比活度不能直接测量, 通过公式(1)、(2)计算得到。由此看出, 24Na比活度的测量的关键就是24Na放射性活度的测量。

|
(1) |

|
(2) |
24Na的放射性活度测量可以分为整体测量和(血液)样品测量。大体上看, 样品测量的精度高于整体测量, 而且一般整体测量的设备都比较大。
1.1.1 整体测量即使用全身计数器测量全身放射性活度。整体测量更灵敏(通常为样品测量的数百倍)但需要使用特殊设备, 并要求人体皮肤和衣服没有污染(W.G.Cross等人[4], 1985年)。该测量方法因探头与被测人体之间的位置关系不同而有2种测量几何条件。
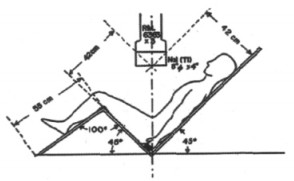
一种是W.B.C.测量系统(丸山隆司等人[1], 1966年), 用于对人体模型和成人的全身24Na放射性进行测量。该测量方法的测量几何条件如图 1。使用W.B.C.测量系统测量24Na的最低活度为14.8Bq。
|
图 1 标准椅的测量几何条件 |
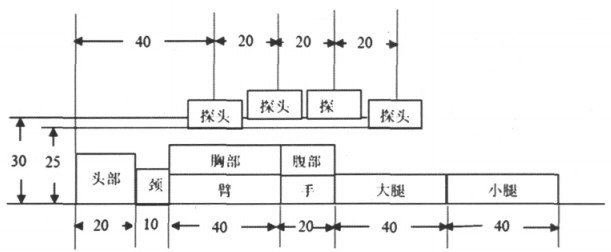
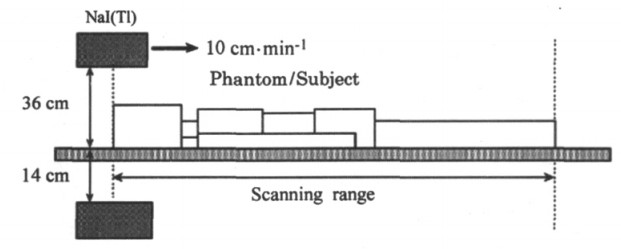
另一种是将探头水平排列的测量方法。其中一个测量全身24Na放射性时体模与探头的位置(李焕铁等人[2]1975年)如图 2。这与另一个全身计数器(T.Ishikawa[6], 2003年)的测量几何条件(如图 3)极其相似, 但相互之间略有区别。图 2中是由4个探测头组成的探头组, 用于测量计数效率和本底, 以及全身24Na放射性测量下限。而图 3中是两个探头, 上下各有一个, 以10cm/min的速度移动扫描。
|
图 2 全身24Na测量人体模型相对探头的位置单位:cm |
|
图 3 全身计数测量几何条件 |
整体测量方法的关键还在于探测器的效率刻度。W.B.C.的校正是使用了三位口服了24Na溶液的成人和相同浓度的模型作了比较。其他实验中, 均是使用体模进行效率刻度。相比较而言, W.B.C.的校正方法测量获得的数值更接近实际值。
1.1.2 样品测量样品测量包括全血测量和血浆测量, 即通过探测器测量血液样品的放射性活度。有研究表明:测量个体血浆中的感生24Na比全血中的24Na更精确(R.H.Mole等人[3], 1984年)。在条件允许的情况下, 可以用离心全血(包括血浆、血小板、白细胞和红细胞)的方法得到血浆。
离体全血测量的具体步骤总结如下:①取样。从受照个体抽取20mL血液放入采样瓶中(Y.Feng等人[7], 1993年)。可加1 mg肝磷脂锂(或其它无钠抗凝剂)到样品中防止凝结(W. G.Cross等人[4], 1985年)。②处理。放置4.5h, 去除短寿命核素(38Cl和49Ca)干扰(李焕铁等人[2], 1975年)。③将装有血液样本的采样瓶放入计数器中计数, 计数时间一般取10~60min (取决于需要的最低可测活度)。④读取读数, 并记录。这里得出的读数只是血液中24Na的相对活度, 而要除以探测效率后才能得到24Na的绝对活度。
1.2 23Na的含量与整体测量和样品测量相对应, 23Na的含量分为全身23Na的含量和血液样品中的23Na的含量。
1.2.1 全身23Na的含量这是采用全身测量方法中一个存在广泛争议的步骤, 在计算比活度时人体内23Na的含量在各参考文献中不一致。根据国际辐射防护委员会参考人的资料[12], 人体23Na含量为1.4g/(kg体重)。其他一些参考文献报告了不同的钠含量。SEKIGUCHI报告说的钠含量是0.92~1.61g/ (kg体重)(T.Ishikawa[6], 2003年)。
1.2.2 血液样品中的23Na的含量23Na在血液中的浓度平均值为1.92mg/mL (W.G.Cross等人[4], 1985年)。而有文献表明(王继先等人[10], 1998年)中国参考人血液中23Na的浓度为(2.211±0.333) mg/mL, 与1.92mg/mL相差3%。由于1975年作为ICRP第23号出版物发布的文件中定义的参考人为生活在平均气温10~20℃的西欧和北美的高加索人, 年龄在20 ~30岁, 体重70 kg, 身高170 cm的男性。这是针对西欧和北美核设施和核企业工作的放射性工作人员定义的, 代表的是西欧和北美的白种人成年男性。这与中国参考人男性身高170 cm, 体重60 kg, 女性身高158 cm, 体重52kg本身就存在差异, 所以血液中的23Na的平均浓度存在差异也属正常。
体内元素也受到其它几个因素的影响。首先, 元素在性别之间是存在差异的, 一般都是男性高于女性(王继先等人[10], 1998年)。其次, 体内元素含量的年龄差异近年来已引起重视, ICRP第56号(1990)、第67号(1994)、第69号(1995)、第71号(1996)以及第72号(1996)出版物相继提出了公众成员摄入放射性核素所致剂量的年龄依赖关系。日本学者(M. Yukawa)对以上两点都有类似的报道。对造成环境污染的有害元素来说, 一般情况下体内蓄积量也随着年龄的增长而相应增加。人骨中Pb含量随年龄的增长而增高的事例已经有报道证实(O'conner[9], 1980年)。23Na元素会不会也有这样的影响?这是需要进一步考虑的问题之一。
1.3 24Na比活度的计算利用公式(1)和(2)计算出全身24Na的比活度和血液24Na的比活度。如果24Na的放射性活度的测量和23Na的含量没有争议的话, 就能顺利获得24Na的比活度了。
2 由24Na的比活度转换为剂量的方法 2.1 由人体全身24Na的比活度转换为剂量首先使用衰变常数(15h物理半衰期和10h的生理半衰期)估算24Na在照射结束时的放射性。其次, 根据国际辐射防护委员会参考人的资料。人体内钠的总量=1.4g23Na/(kg体重)×体重。根据公式(1)计算出24Na的比活度。最后, 利用公式中子剂量=24Na的比活度×0.066(mGy)(T.Ishikawa[6], 2003年)估算出中子剂量。在整个计算过程中, 由于比活度和剂量转换系数的不确定性, 最终剂量值的误差最大可达到50%。
2.2 由人体血液24Na的比活度转换为剂量最简单直接的方法是找出人体血液中24Na的比活度与中子剂量的转换因子, 依照2.1中的公式直接算出。在如何利用24Na活度上, 各方法之间略有区别。
2.2.1 24Na的比活度与中子剂量的转换因子日本原子能研究所的研究人员(F.Takahashi等人[5], 2003年)给出了一些数据。包括不同大小的模型从24Na的活度到全身剂量的转换因子和在不同照射几何条件下从24Na的比活度转换为全身中子剂量的转换系数。这种方法简单、直接, 但前期准备工作量大, 需要提前准备各种照射条件下24Na的比活度与中子剂量的转换因子。
2.2.2 24Na的活度与中子剂量的转换因子在这种方法中引进了中子谱平均剂量——注量转换因子的概念(罗素明[13], 1997年):
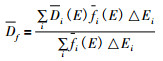
|
(3) |
式中:Di(E)为中子能量从E到E+△E的能量间隔吸收剂量-注量的平均转换因子; fi (E)为能量从E到E+△E的平均谱因子; △Ei为能量间隔。
根据典型裂变中子谱求得Df, 在实验条件下是已知受照热中子积分通量φ, 则受照总剂量D为D=Dfφ。血液绝对活度A0可测。则剂量与活度的转换因子计算公式为:

|
(4) |
其中, Ao为样品的放射性活度; F为样品的转换因子。
用同样的方法, 可以求出镭-铍源、镅-铍源和锎-252源的F值。
在事故情况下, 只要测出血液绝对活度Ao值, 根据公式
(2) 算出总剂量值。使用该方法的前提条件是要建立F值和热中子积分通量的对应关系。
2.2.3 24Na活度与32P的活度比与中子剂量的转换因子该方法(E.S.da Fonseca等人[12], 1996年)中引入了转换因子Fconv与32P和24Na的比活度的概念。利用线性插值调节。给出了调节方程:
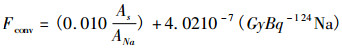
|
(5) |
这里, 转换因子Fconv的获取依赖于24Na和32P的活度。
主要的优点是:以前中子谱的资料不需要知道, 测量方法不需要运用模型, 不需要使用任何剂量仪表, γ射线不会影响结果。缺点是:毛发中32P的活度也需要测量。
3 对中子剂量估算产生重要影响的因素及其校正因子 3.1 测量血液中24Na放射性活度时选用的光峰24Na在衰变时发射出两种能量的γ光子, 一个能量是1.368MeV, 另一个能量是2.754MeV。有文献(Y.Feng等人[7], 1993年)表明1.368MeV的光峰用来计数24Na活度比2.754MeV的光峰效率更高。但在低活度条件下, 40K1.46MeV的峰总在人体内存在, 干扰24Na的1.368MeV的峰, 因此计数24Na的2.754MeV能量的峰有更好的统计结果(W.G.Cross等人[4], 1985年)。
就目前的应用来看, 选用1.368MeV的峰比较有优势。原因有以下三点:①2.754MeV的γ射线的能量在已知同位素源中是最高的, 且在该能量附近没有可供利用的标准放射源用于能量刻度。只能通过曲线拟合的方法外推, 其误差较大; ② 1.368MeV的绝对强度100%高于2.754MeV的绝对强度99.85%;③在高活度情况下, 1.368MeV峰的探测效率高于2.754MeV的峰。
3.2 24Na的衰变校正人体24Na活度衰变校正包括物理衰变校正和新陈代谢衰变校正(或生理衰变校正)。当照射超过1小时时, 还需要对照射过程作衰变校正。
3.2.1 物理衰变校正对于38Cl、49Ca和40K进行校正, 对于38Cl来说, 4h后还剩6.25%;对于49Ca来说, 35min后就剩余6.25%;对于40K来说, 4h后还剩79%, 但其活度低, 计数的影响很小。全血中可能还存在56M (0.85MeV的小峰)以及微量的长半衰期β放射性成分存在, 而血清中没有。但这些对24Na的放射性测量没有多少影响。
按照放射性核素的衰变规律, 我们可以通过下列公式算出照射产生的24Na活度, 则
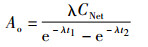
|
(6) |
式中:λ为24Na的物理衰变常数。取值为7.7×10-4 min-1; CNet为净计数; t1为中子源照射结束后到计数开始时的时间间隔; t2为中子源照射结束后到计数结束时的时间间隔;
3.2.2 新陈代谢衰变校正如果照后几天全身计数和血液采样未进行, 还需要对24Na的排泄进行修正。在仍关心感生24Na活度时(1周), 这种衰减基本上按照10.7d的生理半排期指数减弱(W.G.Cross等人[4], 1985年)。美国橡树岭实验室的技术手册[7]中给出了半排期为12d的校正因子表达式。
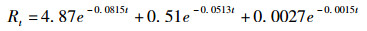
|
(7) |
式中:Rt为是在样本采集时初始仍在体内的份额, t是事故发生后的天数。
3.2.3 照射过程的衰变校正照射时间超过1 h时的校正因子为
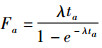
|
(8) |
式中:Fa为衰变校正因子, λ为的24Na衰变常数, 7.7×10-4 min-1, t a为照射时间(min)。
经过三次校正后, 24Na的比活度的计算公式为:
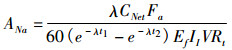
|
(9) |
式中:ANa为在血样中浓度(Bq/mL); CNet为在1.368MeV能峰上的净计数, λ为24Na的衰变常数; 7.7×10-4 min-1, t1为从照射结束到计数开始经过的时间(min); t2为从照射结束到计数结束经过的时间(min); Ef为在1.368MeV处的探测效率, II为1.368MeV的γ射线强度, 100%;V为血样总体积(mL); Rt为新陈代谢校正因子; Fα为照射衰变校正因子。
3.3 在辐射场中人体与辐射源的相对距离美国加利福尼亚大学的Hankins研究认为(DALE.E.Hankins[13], 1980年), 血钠的比活度随着人体与辐射源相对距离的增加而增加。但这种增加是由于散射和低能中子引起的。也就是说人体与辐射源的相对距离的增加而引起的血钠比活度的增加不是单一原因引起的, 多种原因应该综合考虑。
3.4 临界装置和人之间的屏蔽层美国橡树岭实验室12028技术手册[7]中的剂量转换系数表格中对屏蔽层的种类和厚度作了比较齐全的比较。同一屏蔽物, 厚度越厚, 产生的剂量越小。
3.5 中子的地面散射和墙壁散射地面和墙壁的反射对24Na活度与剂量的比值有很大的影响, 因为散射中子能量低, 对剂量贡献小, 对活度贡献大(W.G.Cross等人[4], 1985年)。如果人体23Na反应达到饱和, 那对剂量的估算没有太大的影响, 如果人体受照剂量本身就很小, 且照射时间短, 人体内的24Na的活度与剂量之间的比值就会受到较大的影响。1981年, 克洛斯实施了一个实验, 使用一个裂变中子源在3 m远处照射模型来观察散射效应。结论是中子地面散射是正面直接入射的中子产生的放射性的1.43倍(Y.Feng等人[7], 1993年)。如果对这种混合辐射场的换算系数进行评估, 则必须要对相关能谱的单能粒子换算系数进行适当的平均(ICRP Publications 74[14])。
3.6 人体的尺寸一种结论认为, 小的表面积与体积的比值补偿了大的俘获几率, 对人体活度变化没有显著贡献(Y.Feng等人[7], 1993年)。另一种结论认为, 不同尺寸模型对于相同能量贡献的入射中子来说, 从24Na的比活度到剂量的转换差别小于15%(F.Takahashi等人[5], 2003年)。
3.7 俘获概率个体内的中子俘获概率在当前的计算技术中不是必需的, 因为感生24Na的比活度能够从单位质量23Na的(n, γ)反应率中得出(F.Takahashi等人[5], 2003年)。对于用模型获得的俘获概率, 直径和模型壁对其有影响(W.G.Cross等人[5], 1985年)。
3.8 人体在辐射场中的取向用蒙特卡洛方法计算的结果显示正向照射比侧面照射的俘获几率约高20%。如果在事故中被从侧面照射, 测量的血液放射性在使用活度-剂量转换时需要乘以一个2的因子来估算总的受照中子剂量(Y.Feng等人[7], 1993年)。但从国际放射防护委员会第74号出版物[16]中的附表A41可以看出, 单能中子能量小于100MeV时, 前向照射有效剂量是右侧照射有效剂量的1.23~3.85倍; 单能中子能量大于100MeV时, 右侧照射有效剂量是前向照射有效剂量的1.00~1.22倍。
4 对中子剂量估算方法的前景展望在现有技术的基础上, 利用现有的转换系数, 对各类中子源特性参数进行统计, 建立完整的中子谱库, 将成为提高中子剂量估算速度和精度的关键。
在深入研究快速估算中子剂量技术的同时, 早日实现硬件的便携及其与软件的无缝结合, 成为当前反恐卫勤救援中应急处置大规模公共突发核事故事件的迫切需求。在面临核恐怖事件或中子临界事故时, 中子剂量估算方法必定能为医学应急响应提供剂量学数据, 为正确决策提供科学依据。
| [1] |
丸山隆司, 饭沼武. 事故時における被爆線量の推定[J]. 日本医学放射学会杂志, 26(11): 139-146. |
| [2] |
李焕铁, 朱天成, 谢云瑞, 等. 从人体钠活化测量估算中子剂量[M]. 北京: 原子能出版社, 1975: 60-73.
|
| [3] |
R.H.Mole.. Sodium in man and the assessment of radiation dose after criticality accidents Phys[J]. Med Biol, 1984, 29(11): 1307-1327. DOI:10.1088/0031-9155/29/11/001 |
| [4] |
W.G.Cross, H.Ing.. Activation in the human body[J]. Radiation Protection Dosimetry,, 1985, 10(1-4): 265-276. DOI:10.1093/rpd/10.1-4.265 |
| [5] |
F.Takahashi, A.Endo, and Y. Yamaguchi, et al.Dose assessment from activated sodium within a body in criticality accidents[J]. Radiat Protection Dosimetry, 2003, 106: 197-206. DOI:10.1093/oxfordjournals.rpd.a006350 |
| [6] |
T. Ishikawa, Measurement of the radio nuclide 24Na produced by neutron exposure to the body[J]. Journal of Japan Radiological Society of Medicine, 2004, 26(11): 175-178. |
| [7] |
Y. Feng, K. S. Brown, W. H. Casson, et al. Determination of Neutron Dose from Criticality Accidents with Bioassays for Sodium-24 in Blood and Phosphorus-32 in Hair[Z]. ORNL TM-12028, 1993.
|
| [8] |
Wang Jixian, Chen Rusong, Zhu Hongda, et al. Data of Anatomical Physiological and Metabolic Characteristics for Chinee Reference Man[P]. The First Edition. Beijing: Atomic Energy Press, 1998: 1-6, 177-195.
|
| [9] |
O'connor B H. Level temperal trends of trace element concentrations in vertebral bone[J]. Achives of Environmental Health, 1980, 35(1): 21. |
| [10] |
ICRP. Report of the task group on Reference Man[P]. ICRP Publication 23. Oxford: Pergamon Presss, 1975.
|
| [11] |
罗素明. 测量人体血液中估算中子事故剂量[J]. 中华放射医学与防护杂志, 1997, 117(5): 338-340. |
| [12] |
E.S.da Fonseca, C.L.P.Mauricio. Estimate of the Absorbed Dose Received by Individuals Irradiated with Neutrons[J]. Radiation Protection Dosimetry, 1996, 67(2): 147-149. DOI:10.1093/oxfordjournals.rpd.a031808 |
| [13] |
DALE.E.Hankins. Dosimetry of criticality accidents using activations of the blood and hair[J]. Health Phys, 1980(38): 529-541. |
| [14] |
国际放射防护委员会第74号出版物. 外照射放射防护中使用的换算系数[P]. 北京: 原子能出版社, 1998: 67-96, 242-275.
|




