2. 东华理工大学放射性地质与勘探重点学科实验室, 江西 南昌 330013;
3. 东华理工大学核工程技术学院, 江西 抚州 344000
氡(222Rn)是一种无色、无味的放射性气体, 广泛存在于人们的日常生活环境中。对于生活在室内的人员来说, 空气中的氡约有56%左右来源于建筑物底层土壤。虽然随着水泥等材料生产能力的上升, 使得现代建筑中氡的主要贡献源发生变化, 但建筑物底层土壤还是室内空气中氡的第二大源泉[1, 2]。对于室外空气中氡, 土壤所析出的氡是主要来源。据国内外资料显示, 地面壤氡析出率是表征空气中氡的最佳参数(即能很好地描述氡的地质潜势), 该参数不仅考虑了岩性、构造等地质因素, 而且将土壤、岩石中的氡对空气中氡的影响及氡在岩石、土壤中的动态运移也考虑在内了, 所以研究壤氡析出率就显得尤为重要了。
目前对于土壤氡析出率的测量方法很多, 常用的有两种—活性炭吸附法和积累法。虽然前者取样简单, 但须经吸湿度修正、停留时间修正, 测量工作繁琐。一般野外测量多选前者, 但由于需采用累积腔室, 而扣在地面上的累积腔室中的氡浓度会受到两方面的影响:倘若密封性不够, 将导致腔室内、外的氡由于浓度差形成扩散; 累积一定时间后, 当腔室内氡浓度大于壤氡浓度时, 累积停止(积累腔下土壤中氡从腔室密封区外析出), 甚至形成反扩散。这就是氡析出率测量中长期困扰测量工作者的两大难题—泄漏与反扩散。之后有人[3]提出流气贯穿法, 在一定程度上解决了反扩散所带来的影响。但由于装置较复杂、对测氡仪灵敏度要求较高, 不适宜野外测量。下面介绍几种区域壤氡析出率快速预测方法。
1 扩散模型法222Rn是由226Ra衰变产生的一种气载放射性产物, 而镭在所有的陆地物质中都存在。在226Ra衰变过程中, 氡借助反冲作用从材料的固体基质中释放出来。进入有空隙空间的氡原子则靠扩散及经该空间的对流作用被输运, 直到它们衰变或被释放到大气中[4, 5]。根据气体对流与扩散的理论, 可得出氡在陆地运移理论公式。由于地面的氡析出率实质上等于土壤向大气运移的氡通量, 那么地面氡析出率理论公式为:
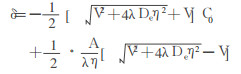
|
(1) |
式中, δ:为壤氡析出率; C0:地面处大气中氡浓度; V:氡在土壤中的对流速度; λ:氡的衰变常数; D e:氡在土壤中的有效扩散系数; η:土壤有效孔隙度; A:单位体积土壤中产生的活动氡。
但由于氡在土壤中的对流速度需要实地分析测量, 准确分析困难。近年来多采用一维扩散模型来预测壤氡析出率[6-8], 其理论公式为
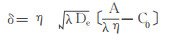
|
(2) |
式中, 各符号意义同上。由于空气中氡浓度对预测结果影响很小, 且增加预测时间, 故一般省略不计。则上式化简为
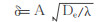
|
(3) |
Rogers和Nielson[9]对不同的土壤温度、含水饱和度下氡的有效扩散系数实验中拟合得出氡扩散系数随土壤的温度T、含水饱和度S变化的经验公式为
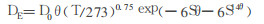
|
(4) |
式中, D0=1.1×10-5 m2/s为氡在自由空气中的扩散系数; θ=(93.947-32.995×p)/100为土壤总的孔隙度[10]; p为土壤容重。
对于土壤含水饱和度S, 可按下式计算[7]

|
(5) |
式中, ω为土壤质量含水率; α为水的密度, 通常取1000 kg/m3; 其他符号同上。
从上面分析可以得出, 只要知道取样点(或待分析点)单位体积土壤中产生的活动氡量A、土壤容重p、土壤温度T、土壤质量含水率ω就可以预测出该点的壤氡析出率。在这些参数中, 唯一难确定的只有A, 其他参数均可通过一定技术手段测量得出。下面根据单位体积土壤中产生的活动氡量A的预测方法不同分类讨论。
1.1 226Ra法由于226Ra是222Rn的母体, 通过对待调查区域土壤布点采样, 通过实验室γ能谱分析[11]或对地γ能谱分析[12]得出各点土壤中所含226Ra的比活度CRa。根据射气系数的概念, 便可得出单位体积土壤中产生的活动氡量A的计算公式为
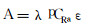
|
(6) |
式中, CRa:土壤中226Ra的比活度; ε:土壤射气系数, 其他符号意义同前。
土壤射气系数ε与土壤的颗粒大小、含水饱和度(水在土壤空隙中所占的体积百分比)及温度相关[13]。根据实测数据回归拟合得出土壤在温度为T、含水饱和度为S时的射气系数ε的经验公式[6, 13]为
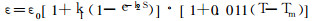
|
(7) |
式中, ε0:为温度为Tm经烤干水分的土壤的射气系数; 其它未知系数见表 1。
|
|
表 1 氡析出率与土壤含水量、温度回归系数[13] |
该模型应用相当广泛, ZHou[13]通过该模型对韩国及日本十个样品进行预测, 虽然对单个样品预测值与实测值相对误差最大达到24.6%, 但其平均值相对误差为10.09%;孙凯男[7]应用此模型对北京地区壤氡析出率进行预测, 得到北京地区壤氡析出率为16.7mBq·m-2·s-1, 与对该地区实测值17mBq· m-2·s-1相比, 相对误差约1.8%, 说明此方案合理可行。
1.2 238U法通过测量土壤中238U的含量(取样深度一般为80~100cm[8]), 并在一定的经放大的采样网络上对所采样品进行铀镭平衡系数分析, 得出土壤样品中镭含量, 进而转化为单位体积土壤中产生的活动氡量A, 其理论计算公式为
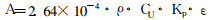
|
(8) |
式中, ρ:土壤密度; Cu:土壤中铀含量; Kp:土壤的铀镭平衡系数; ε:土壤射气系数。
刘庆成等[8]应用该模型对北京地区进行壤氡析出率预测, 发现测量值与预测值相对误差仅为4.4%, 证明该方法可行。
式(8)反映了壤氡析出率与其对应的地质背景中铀的分布与含量水平有密切关系。这为利用我国目前已有的380万km2的航空放射性测量资料和近600万km2的区域地球化学资料中的铀含量数据进行区域壤氡析出率快速预测奠定了基础。本课题组通过航空γ能谱资料分析, 对新疆某沙漠地区进行壤氡析出率预测, 但由于缺乏相应的地球化学资料, 采用砂质土壤同一计算参数, 得出预测值比实测值略高, 相对误差为10.03%[14]。
2 陆地γ剂量率法各点陆地γ剂量率空间变化源于土壤中放射性核素迁移, 实验证明至少有约60%左右是源于土壤氡的空间变化[15]。这说明壤氡析出率在一定程度上与待测点陆地γ剂量率存在一定关系。
经调查发现, 虽然单一点上土壤中所含238U衰变系列对该点陆地γ剂量率贡献不一(12%~90%), 但是对某一地区而言却是比较稳定的(如西班牙为27%, 意大利西北部为29%, 瑞士的塞浦路斯为30%[15])。从上述快速预测方法可以看出, 除226Ra/238U含量外, 其他参数均采用区域平均值或相同土壤质地样品测量数据的典型值, 也就是说土壤氡析出率与该点土壤中238U的含量成正比。而区域土壤中238U衰变系列对该点陆地γ剂量率贡献稳定, 那么就可以通过陆地γ剂量率来预测区域壤氡析出率。
但目前各国所拥有的γ剂量率测量数据是离地高度1m处的空间γ剂量率, 该数据是探测器的内在本底(在没有辐射存在的区域γ剂量率探测器的测量值[16])、陆地天然放射性(238U、232Th系列以及40K)、人工放射性(主要是137Cs, 来源于人类核试验以及1986年的切尔诺贝利事故)以及宇宙γ射线的贡献之和, 这也是为什么在UNSCEAR2000年报告中显示[4]:在假定各国土壤核素浓度的测点均满足离地面1m高处空气吸收剂量率转换模型计算条件下, 由核素浓度计算和直接测量所得的国家平均值差别超过30%时。所以在根据陆地γ剂量率来预测区域壤氡析出率时, 由于不同厂家所产生的γ剂量率仪的内在本底不同, 甚至是同一厂家所生产的同一款仪器的内在本地均不相同, 各监测点土壤所含人工放射性核素的量、宇宙γ射线强度也不相同, 所以必须先从所测γ剂量率中扣除探测器的内在本底、人工放射性以及宇宙γ射线的贡献, 从而得到该点的陆地γ剂量率。而且在雨天或地面受冰雪覆盖时, γ剂量率的测量值比真实值小10%左右[16]; 不同季节, 不同时间段, 大气压强不同, 宇宙γ射线的贡献也不近相同; 测量一次γ剂量率, 不同类型仪器, 不同工作者所采用的测量时间间隔也不相同, 这些因素均必须经过修正。
由于位于地下900m以上深度的岩盐矿井内宇宙μ介子浓度与地面相比低5倍[17], 岩石的天然放射性像222Rn的浓度很低。根据欧洲某地下放射性检定及光谱分析实验室测量结果显示, 这些岩盐矿井中周围的剂量〔H*(10)〕当量率远低于1nSv/h, 该值足够低, 近似认为是没有辐射存在的地区, 可用于估计探测器的内在本底。
宇宙放射性与大气压互为函数关系[18]。探测点海拔越高, 大气压越低, 宇宙射线的贡献越大。由于气压的变化, 不同时刻同一点的宇宙射线的贡献也并不相同, 气压波动可能导致±3nSv/h的γ剂量率变化。通过航空测量方法, 在某一湖面上, 进行γ剂量率随高度变化不同的实验, 根据实验数据规律, 可消除因测量点海拔高度不同对γ剂量率测量结果所带来的影响。
137Cs的半衰期很长(30.2a)且稳定性很强, 导致现今为止土壤中均存在。残留的137Cs来自于核试验的远多于切尔诺贝利事故, 估计范围约为1~4kBq/m2[4]。由于137Cs迁移至土壤中, 受到源位与地表间土壤衰减的影响, 导致地表γ剂量率测量值降低。但是, 在大部分土壤中, 137Cs的垂直迁移率很低, 约0.1~0.2cm/a。而137Cs自身衰变比上述原因对地表γ剂量率测量值影响更大。通过137Cs在土壤中深度不同, Bossew等人[19]经测量得出适用于沉积10年或更长的137Cs的γ剂量转换系数1nSv·h-1/(kBq·m-2)。这样就能修正并消除人工放射性核素的贡献份额。
T.Szegvary等人[15]通过对欧洲部分地区(瑞士、德国、苏格兰)已知测点的陆地γ剂量率与壤氡析出率测量值分析得出一拟合度为0.66的壤氡析出率预测公式
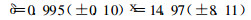
|
(9) |
式中, δ:为壤氡析出率, Bq·m-2·h-1; x:待预测点陆地γ剂量率, nSv·h-1。
根据该公式, 分别对芬兰南部、芬兰北部以及匈牙利进行壤氡析出率预测(结果见表 2), 预测结果与实测值符合的非常好, 说明该方法可行。
|
|
表 2 陆地γ剂量率模型预测壤氡析出率(Bq·m-2·h-1)[16] |
综上所述, 由于对区域壤氡析出率定点测量效率低下, 且随着土壤核素迁移, 各点壤氡析出率不断变化, 必须借助一定技术手段进行区域壤氡析出率快速预测。
现行的区域壤氡析出率快速预测方法很多, 且预测值与实测值的偏差均低于10.1%。不同地区可根据已有数据资料选择不同模型进行壤氡析出率快速预测, 以圈定高氡区, 指导除氡降氡和建筑物的选址, 以达到减少因氡及其子体影响引发肺癌几率的目的。
对于我国目前已拥有380万km2的航空放射性测量资料, 通过航空γ能谱数据, 推测区域238U含量, 结合各区域地球化学参数, 预测壤氡析出率, 以圈定高氡区, 显得尤为方便、快捷, 且准确性很高。
| [1] |
Michel van der Pal, geboren te Hoom.Radon transport autoclaved aerated concrete[R].Eindhoven University of Technology, Eindhoven, Netherlands, 2004.
|
| [2] |
de Jong P., van Dijk W., vander Graaf E.R., de Groot T.J.H.. National survey on the natural radioactivity and 222Rn exhalation rate of building materials in the Netherlands[J]. Health Physics, 2006, 91(3): 200-210. DOI:10.1097/01.HP.0000205238.17466.1c |
| [3] |
潘自强. 电离辐射环境监测与评价[M]. 北京: 原子能出版社, 2007.
|
| [4] |
UNSCEAR.Sources and Effects of Ionizing Radiation, Volume1[R].Sources United Nations, New York, 2000.
|
| [5] |
刘庆成.环境氡理论与应用研究[Z].北京: 北京科技大学.[博士后论文], 1998.
|
| [6] |
Goto Masayoshi, Jun Moriizumi, Hiromi Yamazawa, et al. Estimation of global radon exhalation rate distribution[J]. American Institute of Physics, 2008, 1034(1): 169-172. |
| [7] |
Sun Kainan, Guo Qiuju, Zhou Weihai. Feasibility for mapping radon exhalation rate from soil in china[J]. Journal of Nuclear Science and Technology, 2004, 41(1): 86-90. |
| [8] |
刘庆成, 吴信民, 刘玉娟, 等. 北京市城区的氡地质潜势规律研究[J]. 核技术, 2009, 32(1): 55-60. DOI:10.3321/j.issn:0253-3219.2009.01.013 |
| [9] |
Rogers V C, Nielson K K. Multiphase radon generation and transport in porousmaterials[J]. Health Phys., 1991, 60: 807-815. DOI:10.1097/00004032-199106000-00006 |
| [10] |
中国科学院南京土壤研究所土壤物理研究室. 土壤性质物理测定法[M]. 北京: 科学出版社, 1978.
|
| [11] |
Verdoya M, Chiozzi P, De, Felice P, et al. Natural gammaray spectrometry as a tool for radiation dose and radon hazard modelling[J]. Applied Radiation and Isotopes, 2009, 67(5): 964-968. DOI:10.1016/j.apradiso.2009.01.066 |
| [12] |
付锦. 用γ能谱测量确定铀尾矿氡析出率的可行性[J]. 铀矿地质, 2003, 19(3): 167-173. DOI:10.3969/j.issn.1000-0658.2003.03.007 |
| [13] |
Zhou weihai, Iida Takao, Furukawa Masahide. Modeling Radon Flux Density Fromthe Earth's Surface[J]. Journal of Nuclear Science and Technology, 2006, 43(4): 479-482. DOI:10.1080/18811248.2006.9711127 |
| [14] |
刘艳阳, 刘庆成, 张志勇, 等. 利用航空γ能谱资料快速预测环境氡浓度[J]. 资源调查与环境, 2007, 28(1): 68-73. DOI:10.3969/j.issn.1671-4814.2007.01.011 |
| [15] |
Szegvary T, Leuenberger MC, Conen F. Predicting terrestrial 222Rn flux using gamma dose as aproxy[J]. Atmospheric Chemistry and Physics, 2007, 7: 2789-2795. DOI:10.5194/acp-7-2789-2007 |
| [16] |
Stöhlker U, Bleher M, Szegvary T, et al. Inter-caliberation of gamma dose rate detectorson the European scale[J]. Radiop rotection, 2009, 44(5): 777-784. DOI:10.1051/radiopro/20095140 |
| [17] |
Szegvary T, Conen F, Stöhlker U, et al. Mapping terrestrial γ-dose rate in Europe based on routine monitoring data[J]. Radiation Measurements, 2007, 42(9): 1561-1572. DOI:10.1016/j.radmeas.2007.09.002 |
| [18] |
Wissmann F, Rupp A, Stöhlker U. Characterization of dose rate instruments for environmental radiation monitoring[J]. Zeitschrift Kerntechnik, 2007, 4: 193-198. |
| [19] |
Bossew P, Ditto M, Falkner T, et al. Contamination of Austrian soil with Caesium-137[J]. Environmental Radioactivity, 2001, 55: 187-194. DOI:10.1016/S0265-931X(00)00192-2 |



 ,
, 
