在人员对核部件进行操作时, 受到的辐射种类往往不只一种, 在操作某种核部件时, 最主要的危害来自中子和光子, 为保护操作人员, 一般用手套箱对其进行辐射防护, 由于对中子屏蔽效果最佳的材料和屏蔽光子最佳的材料并不相同, 为使操作人员受辐射伤害最小, 需对室壁的两种屏蔽材料的厚度进行优化, 以达到对两种辐射的最佳屏蔽效果。

1 优化原理

手套箱外壁的厚度为h, 屏蔽由2种材料组成, 它们对光子的衰减系数为f₁(x)、f₂(x), 对中子的衰减系数为g₁(x)、g₂(x), 其中x为该材料的厚度。设无屏蔽材料时人体组织材料对光子与中子的吸收剂量分别为H_γ与H_n, 有屏蔽材料时人体组织材料对光子与中子的吸收剂量分别为G_γ与G_n, 则有如下关系式:

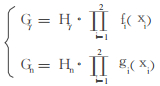
(1)

其中x_i为该材料的厚度。

总剂量为G=G_γ+G_n, 欲使总剂量最小, 则可以由如下约束方程式来计算x_i的值:

(2)

式中h_max为屏蔽材料的最大总厚度。

2 最优化计算 2.1 屏蔽材料的选择

利用MCNP程序^[1]通过如下几何模型来评价不同材料对中子的吸收效果, 其中核材料为内径15cm, 外径16cm, 强度为1Bq的⁶⁰Co球壳, 直径为1cm的水球球心距球壳球心距离为30cm, 通过比较相同厚度(1cm)的不同材料屏蔽后水球的沉积能量来评价何种材料对中子有最佳的吸收效果, 计算结果如表 1。

表 2是高能X射线在不同物质中衰减一半所需要的厚度, 由于X射线的辐射特性与γ射线类似, 可说明对光子具有最好的衰减作用是钨, 其次是铅, 综合考虑成本的问题, 选用铅作为最佳屏蔽材料。通过分析, 选用聚乙烯和铅作为构成手套箱室壁的两种材料。

2.2 最优组合厚度计算

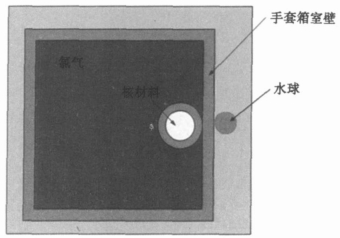
计算两种屏蔽材料对两种辐射屏蔽效果的MCNP计算原理图如图 1所示, 手套箱的室壁厚度为27cm, 用直径为1cm的水球作为人体等效组织, 源材料是一个中心在(0, 0, 0)的均匀分布的Pu球壳, 内径为15 cm, 外径为16 cm的, 密度为16.54gcm^-3。

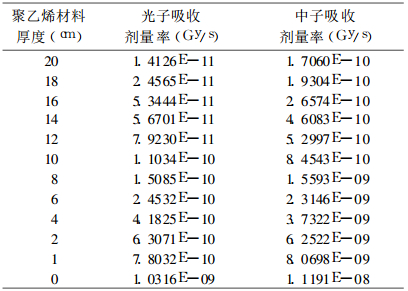
表 3是计算屏蔽材料为不同厚度聚乙烯时, MCNP计算所得人体等效组织的中子与光子吸收剂量率。

通过MATLAB^[2]对数据进行拟合, 得到中子吸收剂量率随聚乙烯厚度变化拟合函数:

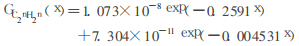
(3)

光子吸收剂量率随聚乙烯厚度变化拟合函数为:

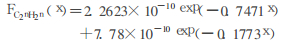
(4)

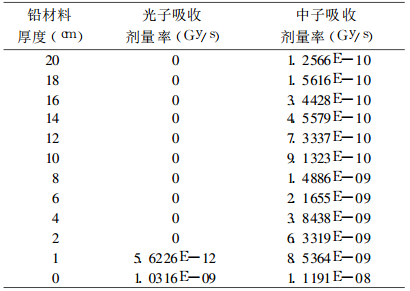
表 4是计算屏蔽材料为不同厚度铅时, MCNP计算所得人体等效组织的中子与光子吸收剂量率。

通过MATLAB对数据进行拟合, 中子吸收剂量率随铅厚度变化拟合函数为:

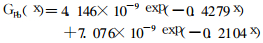
(5)

光子吸收剂量率随铅厚度变化函数为:

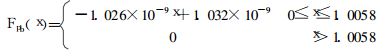
(6)

根据(2)式, 得到优化方程:

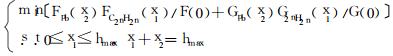
(7)

式中, F(0)、G(0)分别为无屏蔽时光子与中子吸收剂量率; x₁为聚乙烯的厚度, x₂为铅的厚度。

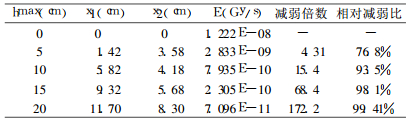
通过优化方程得到最优厚度见表 5, 表中h_max表示室壁总厚度, x₁表示聚乙烯的最优厚度, x₂表示铅的最优厚度, E表示优化后的总吸收剂量率。

3 结论

通过MCNP模拟和MATLAB拟合数据, 对手套箱屏蔽材料进行了优化, 根据计算结果, 可确定手套箱室壁在四种不同厚度下最优的屏蔽方案。