全身计数器是工作人员体内放射性核素种类和活度的测量系统, 是内照射剂量测量与评价的重要设备之一。大多数的全身计数器采用大尺寸的NaI (Tl)探测器, 在探测137Cs的661.66keVγ射线时, 因为探测器的最佳能量分辨率大约为7%, 214Bi 609.3keVγ射线影响其测量, 不利体内137Cs的测量及γ谱分析, 尤其是体内137Cs的活度较低时, 所得137Cs全能峰小, 与214Bi 609.3keV的全能峰形成重峰, 必须进行重峰分析, 否则结果的可信度较差。对于重峰分析方面, 文献[1]只简单介绍了非线性最小二乘非迭代法, 主要顾虑的是当时计算机速度不能满足大量数据反复迭代的需求。但随着计算机技术的发展, 其速度已不再是数据迭代处理的瓶颈, 而且包含非线性曲线拟合方法的应用程序有许多[2, 3], 例如Matlab软件在数据处理中已得到广泛应用, 但其在全身计数器NaIγ谱中的应用, 国内文献[1]主要关注单能全能峰拟合函数选择方面的研究, 在重峰分析方面, 国内报导较少。笔者采用不同活度的137Cs放射性点源, 在全身计数器上获取γ谱, 利用基于Matlab的非线性曲线拟合方法进行重峰分析, 给出214Bi、137Cs的609.3 keV、661.66keV全能峰计数率, 同时弥补系统自身配置的Ma-estro谱分析软件不能进行重峰分析的不足。
1 材料与方法 1.1 实验器材① 由一块截面为10.2cm×10.2cm(4英吋× 4英吋)、长40.6cm(16英吋)的NaI (Tl)探测器、铅屏蔽室、Trump8k多道分析器、Maestro谱采集与分析软件、高低压电源、测量床、计算机等构成的全身计数器测量系统[4]。②含137Cs、60Co核素的标准放射性点源1个。③自制已知活度的137Cs放射性点源9个。
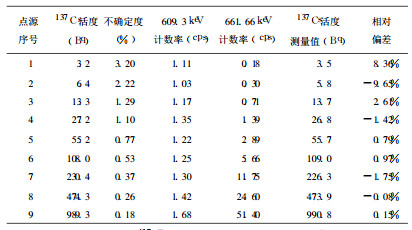
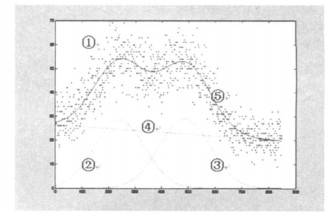
1.2 测量方法与原理将全身计数器的工作参数调整至最佳工作状态, 系统预热1h后, 将137Cs、60Co标准放射性点源放置在NaI (Tl)探测器上方20cm处一固定位置, 进行能量和效率刻度。移走标准放射性点源, 分别将9个自制已知活度的137Cs点源放在同一位置, 采集γ谱5 000s。将每个点源的γ谱中能量范围在552.8keV~ 735.8keV间的感兴趣区域的数据提取出来, 用Matlab软件进行处理[2]。其中4号点源的谱数据显示如下图 1中散点图①所示。
|
图 1 4号自制137Cs放射源的γ谱中感兴趣区域显示与处理结果图 |
进行重峰分析时, 最简单的方法的是:全能峰采用纯高斯函数表示, 基线采用线性函数表示[1]。在Matlab程序中定义下列函数式, 对原始谱数据①进行非线性曲线拟合[3]。拟合曲线图见图 1所示, 其中曲线②、③为两个全能峰, 直线④为基线, 曲线⑤是拟合后的谱图。

|
(1) |
式中, F为拟合的计数; x(1)为曲线②的峰高; xdata为道址; x(2)为曲线③的峰高; x(3)是直线④的斜率; x(4)是直线④的截矩; x(5)为曲线②的中心道址; x(6)为曲线②、③的峰宽度参数; x(7)为曲线③的中心道址。
由式(2)计算曲线②的总计数率n。

|
(2) |
式中, t为谱采集时间, 5 000s。将上式中的x(1)替换成x(2), 可计算出曲线③的总计数率n′。
用标准放射性点源进行效率刻度, 得出探测器对137Cs点源的探测效率ε, 由式(3)计算活度的测量值。
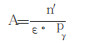
|
(3) |
式中, A是测量分析得出的自制137Cs点源的活度, (Bq); pγ为137Cs的661.66keVγ射线发射几率, 85.1%。
2 结果与分析表 1给出了自制9个137Cs点源的活度, 分析得出的214Bi、137Cs609.3keV、661.66keV全能峰计数率, 由计数率计算得出的137Cs活度测量值以及测量值与已知活度间的相对偏差。
|
|
表 1 137Cs放射性点源的测量分析结果 |
由表 1可见, 当137Cs点源的活度低于13.3Bq时, 分析得出的测量值与已知活度的相对偏差较大, 其绝对值达到10%左右。主要原因是放射性点源的活度较低, 活度不确定度较大, 其次是全能峰的计数率较低, 计数的统计涨落较大。当活度高于27.2Bq时, 相对偏差较小, 其绝对值小于2%, 测量值与已知活度的一致性较好。
3 讨论从图 1的谱图可见, 不进行重峰分析时, 很难选择感兴趣的区域。从表 1可知, 若选择包含214Bi的609.3keV全能峰, 则分析得出137Cs661.66keV全能峰的计数率会偏高1 ~ 2cps。经过重峰分析后, 137Cs活度测量值与已知活度的一致性较好, 表明基于Matlab的非线性曲线拟合重峰分析方法可靠。
在函数式(1)中, 对相邻的两个高斯峰进行重峰分析时, 其峰宽度参数选取了同一值, 并且该值可以用标准放射性点源进行测量得出, 条件是测量系统的工作状态必须一直保持稳定, 即不存在严重的道漂问题。
利用基于Matlab的非线性曲线拟合方法, 对部分工作人员的全身计数器NaIγ谱中感兴趣区域进行重峰分析, 得出了137Cs的全能峰计数率, 结果如下表 2所示。实际应用表明, 该方法是一种简便、快捷、可靠的重峰分析方法之一。
|
|
表 2 工作人员测量谱分析结果 |
| [1] |
庞巨丰. γ能谱数据分析[M]. 西安: 陕西科学技术出版社, 1992: 646-660.
|
| [2] |
清源计算机工作室. MATLAB高级应用-图形及影像处理[M]. 北京: 机械工业出版社, 2000: 5-15.
|
| [3] |
蒲俊, 吉家祥, 伊良忠. MATLAB6.0数学手册[M]. 上海: 浦东电子出版社, 2002: 195-196.
|
| [4] |
成智威, 王勇, 郭梅, 等. 全身计数器的一种简易刻度方法[J]. 中华放射医学与防护杂志, 2008, 4(2): 190-192. DOI:10.3760/cma.j.issn.0254-5098.2008.02.031 |