由于源自吸收效应的影响, HPGeγ谱仪测量效率不仅是γ射线能量的函数, 也是样品密度的函数。采用固定介质密度刻度的效率曲线函数只适合于装样密度等于或接近于该标准源密度的样品分析, 每测量一种密度的样品都必须用相应密度的标准源进行刻度, 或者运用函数的内插外推方法计算^[1]。设法找出对不同能量不同样品密度样品测量效率修正的解析函数, 可以求得在实验刻度范围内任一源密度及γ能量的全吸收峰探测效率。

1 基本原理

考虑探测效率的自吸收校正因子, 引入公式:

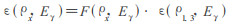
(1)

式中, F(ρ_x, E_γ)为自吸收校正因子, ε(ρ_1.3, E_γ)是固定介质密度(1.3g /cm³)标准源的效率刻度函数, ε(ρ_x, E_γ)为是密度为ρ_x的效率刻度函数。只要我们求出F (ρ_x, E_γ), 则对一个任意密度的混合体源, 其不同能量处的探测效率都可以求得。

2 γ谱仪的性能

实验所用的HPGe探测器的主要性能如下。

2.1 分辨率和相对效率

轴向距离探测器顶端25cm, 对能量为1 332.5 keV的γ射线的分辨率为1.86 keV, 全能峰相对效率48.4%;

2.2 积分非线性

用放射源²⁴¹Am, ¹⁵²Eu, ¹³⁷Cs, ⁶⁰Co的59.4 keV, 121.78 keV, 661.66 keV和1 332.5keV的γ射线全能峰检测系统的非线性, 结果是0.01% ~ 0.28 %;

2.3 系统稳定性

当将⁶⁰Co的1 332.5keV的γ射线全能峰置于6 408道时(全谱为8 192道), 测定的谱仪系统24h谱峰峰位位移为±1.5道。

2.4 系统积分本底

当系统工作在单晶谱仪状态时, 在20keV ~ 2 000keV能区内的积分本底为90.7cpm。

3 标准源设计方案

本次实验使用了3个系列的标准源。

3.1 单核素标准源

²⁴¹Am、²¹⁰Pb、¹⁰⁹Cd、¹¹³Sn— ^113mIn、⁵⁷Co、¹³⁷Cs、⁵⁴Mn、⁶⁰Co、²²Na、¹⁵²Eu、⁵⁶Co和¹³³Ba, 密度均为1.3g /cm³。

3.2 混合标准源

含²⁴¹Am、¹⁰⁹Cd、¹⁵²Eu、¹³⁷Cs、⁵⁴Mn和⁶⁰Co共6种核素, 密度分别为0.3、0.6、0.8、1.0、1.3、1.6、1.8和2.0g/cm³。

3.3 高活度单介质密度混合标准源

含²⁴¹Am、¹¹³Sn— ^113mIn、¹³⁷Cs、⁶⁰Co、⁵⁶Co、¹⁵²Eu、⁵⁴Mn和²¹⁰Pb共8种核素, 密度为1.3g/cm³。

4 固定源密度的效率刻度

为了克服近源距测量的符合相加相应, 采用远近效率比较法刻度HPGe谱仪的端面效率, 分别在近距离和远距离测量介质密度为1.3g /cm³的标准源, 选用¹³⁷Cs、¹¹³Sn、¹⁰⁹Cd三个核素的661.66 keV、391.69 keV、255.06 keV、88.03 keV的四个能量点作远近位效率比曲线拟合, 做出一条ε(近) /ε(远) ~ E(γ)关系曲线, 以此为纽带通过远端拟合函数得到端面效率拟合函数。近源距测量即端面状态测量时, 被分析样品直接放在一个紧贴主探测器端面的有机玻璃样品架上, 待测标准源与探测器的距离为1mm; 远距离测量状态时, 待测标准源与探测器的距离为30cm。探测效率曲线拟合采用的函数形式^[2]为

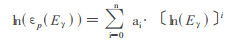
(2)

式中:ε_p为峰面积效率; E_γ为γ射线能量(keV); a_i为第i个待定参数; n值由实验确定。在46.5 keV ~ 3253 keV的整个能量区间内, 探测效率的分段函数的表达式为:

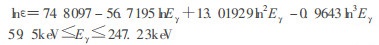
(3)

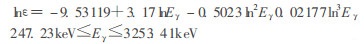
(4)

由式(3)、(4)可求得端面状态无符合相加效应时不同能量(射线的全吸收峰探测效率。

5 固定能量下的自吸收校正函数

为求出F(ρ_x, E_γ), 先只考虑固定能量的γ射线由于吸收物质密度变化引起自吸收校正因子的变化, 选取拟合函数的形式:

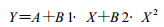
(5)

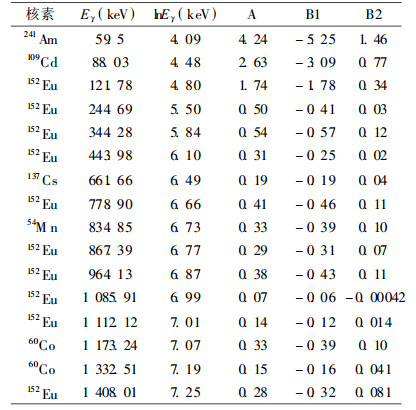
式中, Y表示效率比对数lmF(ρ_x, E_γ); X表示样品源密度(x; A、B1、B2为拟合系数。表 1是各固定能量对应的效率比随密度变化的系数A、B1、B2。

利用表 1给出的各固定能量下γ射线的标准源自吸收校正函数在不同密度下的相应参数值, 再借助于函数值的内插外推方法, 可以算出上述表中未列的其它一些能量γ射线的自吸收校正系数, 这种作法既繁琐又不方便, 利用最小二乘法可以寻求一个对于不同能量的普遍校正函数。

6 不同密度不同能量吸收修正函数

分别研究表 1中A、B1、B2与ln(E_γ)的数据点, 可以发现:从能量起始点59.5keV开始, A、B1、B2的值要么上升, 要么下降, 到一定能量以后, A、B1、B2的值的变化趋缓, 用指数函数来拟合比较合理。为此, 选用Boltzmann方程形式对表 1中系数A, B1, B2与能量关系进行拟合,

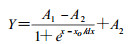
(6)

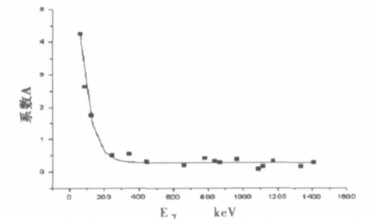
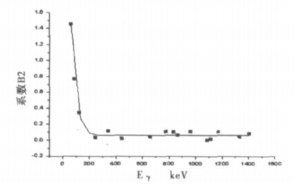
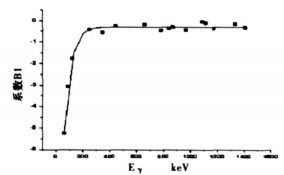
其中, Y =A, B1, B2;A₁、A₂、x₀及dx分别是待定系数。图 1 ~ 图 3分别是系数A、B1、B2的拟合曲线。

将系数A, B1, B2代入公式(5)中, 得到具体的拟合函数的形式(7)。利用该式可以求得在实验刻度范围内任一源密度及γ能量的全能峰探测效率的修正系数。

(7)

7 实验验证和结论

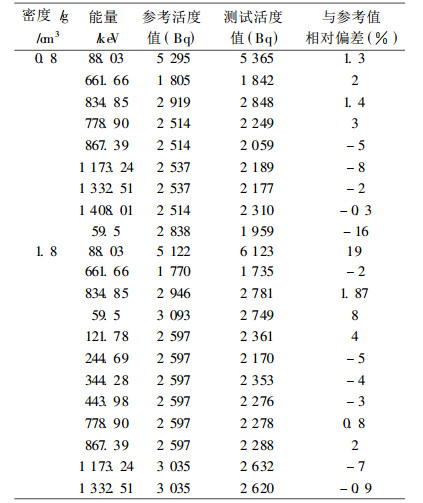
测量了由国家计量院制备的混合体源测试样品, 对(3)、(4)和(7)式进行验证(结果见表 2)。可以看出:应用密度效率修正函数(5), 对于混合源中的单γ发射的核素¹³⁷Cs, ⁵⁴Mn等分析结果与参考值在2倍标准差范围内, 彼此符合得好, 核素¹⁰⁹Cd的分析偏差较大。对于多γ发射的核素来说, 在给定的2倍标准差的不确定度范围内, 绝大部分最大相对偏差不大于5%, 可以完全满足环境样品的低水平放射性测量应用。

选择Boltzmann方程形式拟合函数能忠实地反映实验的数据, 利用给出的修正函数可以求得在实验刻度范围内任一源密度及γ能量的全能峰探测效率, 省去了每测量一种密度的样品都必须制备相应密度的刻度源的繁琐操作。