2. 南方医科大学生物医学工程学院
近年来, 调强放射治疗(intensity modulated radiotherapy, IMRT)技术取得了长足进步, 国外已形成了IMRT治疗计划系统开发及临床应用的研究热潮[1, 2]。相对而言, 国内尚处于起步阶段[3, 4], 基本还没有自主知识产权的IM RT计划系统。我们在对国内外同类软件进行深入研究的基础上, 以第一军医大学开发的JX-100型X刀系统为前期平台, 初步完成了基于遗传算法的IMRT治疗计划系统的设计与开发。
1 材料与方法 1.1 系统开发环境硬件系统采用PC机, 基本配置为:P4 2. 4GHz 512M 80GB; 操作系统采用Windows XP视窗环境, 软件开发平台采用基于Framework2.0框架的Visual C #.Net2005。
1.2 IMRT计划系统模块根据IMRT计划系统设计流程, 系统包含了计划存取、窗宽与窗位调整、感兴趣区域轮廓勾画、射野等中心确定、射野参数选择、处方剂量给定、目标函数定义、优化参数设定、剂量计算、逆向计划优化、优化结果评估、计划输出等模块。
1.3 系统主要功能实现 1.3.1 窗宽、窗位调整窗宽是指需要显示图像的范围, 窗位也称窗中心, 表征显示区域的中心位置。所谓调窗处理就是根据预知的窗宽和窗位值, 获得需要显示的窗口大小和中心位置, 从而将窗口内的值转换成显示时的最亮和最暗范围内的值, 高于窗口灰度范围的部分置为最亮, 低于窗口灰度范围的部分置为最暗。为提高精度, 采用半精度法对窗口范围内的图像数据进行调整, 公式为: 
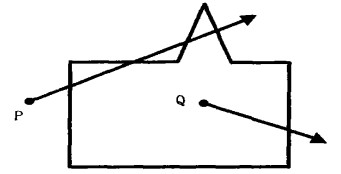
轮廓是由一系列点及相邻点之间的连线构成的, 勾画过程中只要获取了这些点的坐标, 就可以对轮廓进行显示、存储、读取、修改和删除等操作, 为此我们创建了一个链表来保存这些有序的点, 将每次鼠标点击或移动响应的当前坐标加入到链表末端作为下一个点。为判断某点是否在某个勾画的器官内, 定义了一个ContourRegion类来表示一个闭合轮廓线构成的不规则区域, 并为上述类定义了IsVisible()方法, 该方法通过奇偶规则来判断一点是否在区域内:从位置P到对象坐标范围以外的远点画一条射线, 并统计沿该射线与各边交点的数目, 如与这条射线相交的多边形边数为奇数, 则P为区域内部点, 否则为外部点。另外为得到精确的边数, 必须确认所画的直线不与任何多边形顶点相交, 图 1示例了根据奇偶规则对区域外点P和区域内点Q的判断。
|
图 1 奇偶规则对内外点的判断 |
系统提供了手工轮廓勾画基本工具, 包括勾画部位选择、CT图像选取、画线、撤销、删除等功能。勾画部位包括身体外轮廓、计划靶区、危险器官及辅助器官。勾画目的在于剂量计算中求得体内任意点到各轮廓线与射线交点间的距离, 这些距离的计算精度直接影响了形成剂量分布的准确性, 因此, 勾画时每个身体外轮廓一般不少于20个适当选择的点, 以使折线形状尽量与解剖结构的轮廓一致。勾画完成后要进行肿瘤中心的标定, 目的是确定照射时的等中心。
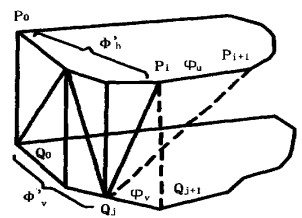
1.3.3 轮廓线的三维重建由上节勾画的一系列二维轮廓线来重建三维形体, 可以归结到由相邻两层的轮廓线重建三维形体的问题上。实现两条轮廓线的三维模型重建就是要用一系列相互连接的三角面片将上下两条轮廓线连接起来, 连接两条轮廓线的众多三角面片来构成相互连接的三维表面, 同时相互之间不能在三角面片内部相交。采用相邻轮廓同步前进法来确定所需要的三角面片:为描述同步准则(图 2), 假设上轮廓线点列为P0, P1 …Pm-1, 下轮廓线点列为Q0, Q1 …Qn-1, 若三角面片已经从起始点连接到Pi和Qj, 上轮廓线中已经完成连接的折线段P0 …Pj的长度为Φ′h, 下轮廓线中已经完成连接的折线段Q0 …Qj的长度为Φv, 线段PiPi+1的长度为φh, 线段QjQj+1的长度为φv, 则下一步选取的三角面片可为ΔPiPi+1Qj或ΔPiQjQj+1。如果|Φ′h+φh-Φ′v| < 1Φ′v+φv-Φ′h|则选取ΔPi Pi+1 Qj, 即沿上轮廓前进一步, 否则选取ΔPiQjQi+1。若上、下轮廓线各有m和n个点, 则用m+n步即可实现相邻两轮廓线之间的三角连接。
|
图 2 同步前进法 |
剂量计算是IMRT治疗计划系统的核心, 剂量计算方法必须给出准确计算结果的同时花费较少的时间, 由于三维卷积模型可以通过快速傅立叶变换实现, 从而大大提高计算速度, 因此我们通过快速傅立叶变换建立了基于笔射束的三维光子卷积剂量计算模型, 其公式为D(x, y, d)=∫∫(x′, y′, d)·k(x-x′, y-y′, d)dx′dy′, 式中ϕ=MUi·CFi· Wij·ROFij·TMRij(P)·ISFij(P)为光通分布, k为卷积核, 其参数具体含义及实现过程已在我们的前期研究成果中做了详细介绍[5]。
1.3.5 逆向计划优化采用遗传算法对IMRT笔射束权重进行优化, 首先对每个笔射束权重采用四位二进制进行编码, 确定初始群体规模, 用随机函数生成初始种群, 并对初始种群进行解码, 然后构建适应度函数(基于剂量的目标函数), 根据个体解码值计算其适应度, 采用最优保存策略, 执行轮盘赌选择、二进制单点交叉和单位置替代变异, 最后根据设定的收敛中止条件, 算法收敛于适应度值最优的个体, 就是要优化的问题的解[6-7]。
1.3.6 计划评估手段等剂量线与三维包络面:二维等剂量线是在某平面内具有某个相同百分深度剂量的点的连线, 能较准确地给出靶区内剂量分布的均匀性、高剂量照射区分布与靶区的适合度以及靶周边和邻近重要器官的剂量变化梯度等情况。等剂量线绘制采用邻域搜索法获得, 并以链码形式存储, 通过处理后将等剂量曲线叠加在断层图像或任意切面的图像上。
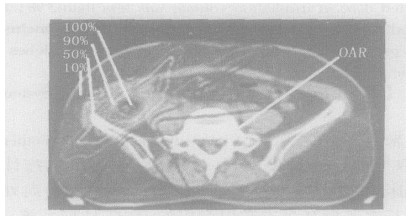
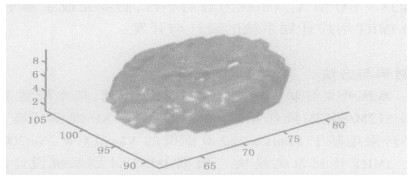
计划靶区的三维包络面可在三维方向上显示剂量分布与靶区的吻合情况, 通过与靶区的三维重建图像相比较, 可以用来评价计划的优劣。逆向计划优化完成后, 我们得到的是一个关于笔射束强度的三维矩阵, 通过将三维矩阵内笔射束强度小于95%和大于105 %计划靶区处方剂量的值赋为0, 然后对其余的值采用三角形贴面方法进行重建, 即可得到三维包络面。实验发现, 如果仅仅保留100 %等剂量点而将其他数据点赋值为0来进行三维包络面的重建, 往往得不到预期效果, 原因可能是100%等剂量点较少, 许多点都在100%等剂量点的附近。对一临床病例, 我们获取了10张连续的CT图片, 经过剂量计算和逆向计划优化后, 绘制的等剂量线和三维包络面如图 3、4。
|
图 3 等剂量线分布 |
|
图 4 三维包络面 |
剂量-体积直方图(Dose Volume-Histogram, DVH):其基本形式是某一剂量区间内出现的体积单元数即频率, 为了计算这个频率, 给出如下画法:首先将感兴趣区划分成体积矩阵, 图 5显示了二维方向上的剂量分布情况:每一个体积矩阵单元内的剂量数字标在相应的单元内。对所要计算DVH感兴趣区域, 一旦计划确定, 都有类似于图 5的矩阵单元分布, 统计每个组织结构内相应剂量区间内的矩阵单元数, 得到DVH图的纵坐标, 假设每个矩阵单元的体积为Vi, 就可以计算出位于相应剂量范围内受照射的总体积, 然后将纵轴上的频率或体积标为仅位于某一剂量水平以上的矩阵单元数或体积的相对数, 即可得到积分DVH。对上面给出的临床病例, 得到的积分DVH如图 6。

|
图 5 DVH计算矩阵图 |

|
图 6 剂量-体积直方图 |
为验证剂量计算结果的精确性, 我们在靶区等剂量线梯度变化较小处选定10个剂量计算点, 用人体放射等效仿真体模进行了绝对剂量验证, 用切片法[8]进行了相对剂量验证(验证计划系统计算的80%等剂量面积与实际照射的胶片测量的80 %等剂量面积按空间位置的面积重合率)。测试结果表明受照体积内任意一点剂量计算不精确度小于3%, 优化结果与测试结果的等剂量线分布面积重合率误差小于5%。
由于IMRT中要优化的参数很多, 因此设计一个计划的时间比较长, 上海拓能2003年引进的WiMRT逆向适形调强放疗系统采用了全散射卷积剂量计算模型, 在主频为XP1800+的双CPU、512MB内存服务器上, 设计一个计划的时间一般在20 min左右。本系统中, 我们建立了基于笔射束的快速傅立叶卷积剂量计算模型, 为提高卷积计算速度, 在计划靶区周围设置了一辅助器官, 从而将剂量计算的笔射束卷积核矩阵缩小到了128 ×128, 有效提高了计算速度, 在P4 2.4GHz 512M个人计算机上执行一个逆向计划, 大约需要40 min。
另外, 等剂量线、剂量-体积直方图等对计划的评估表明, 我们开发的逆向计划系统能够实现高剂量照射区和计划靶区在三维方向的高度适型, 初步达到了所要求的临床目标。目前本系统已获得国家软件著作权, 编号:软著登字第050252号, 软件登记号:2006SR02586。
3 讨论我们研究开发的IM RT治疗计划系统, 已经实现了感兴趣区域的勾画、窗宽与窗位调整、勾画轮廓的三维重建, 基于快速傅立叶卷积的剂量计算、基于遗传算法的笔射束权重优化以及优化结果的评估等功能, 主要完成了下列有意义的探索和尝试:首先通过设置辅助器官来减小卷积核的维数, 成功解决了快速傅立叶卷积剂量计算模型由于要花费大量的时间准备卷积而变得不适合临床应用的问题, 使计算速度大大提高; 其次对传统的基于剂量的目标函数进行了改进, 建立了靶区内剂量均匀性约束、辅助器官和危险器官的最高剂量约束以及组织重要因子约束, 使靶区内剂量均匀性及三维方向上高剂量区与靶区的适形度有了较大的提高; 最后我们用全局优化算法—遗传算法实现了笔射束权重的优化, 研究发现用遗传算法优化IMRT笔射束权重能够得到较高适形度的剂量分布, 而且能以极快的速度达到最优解的90%左右, 对大部分临床应用而言, 已经能够满足实际需求。
由于IMRT逆向计划系统的开发是一个相当复杂的系统工程, 涉及放射物理学、放射肿瘤学、影像医学、计算机图形学、计算机软件开发等多种学科, 我们目前仅仅完成了IMRT系统的大部分功能, 在后续研究中, 我们期望将现有的多种剂量计算及逆向计划优化方法集成的系统中, 并进一步提高计算精度和速度。
| [1] |
Gary A. Genetic and geometric optimization of three-dimensional radiation therapy treatment planning[J]. Med Phys, 1996, 23(3): 393-305. |
| [2] |
Cristian Cotrutz, Lei X. Segment -based dose optimization using a genetic algorithm[J]. Phys. Med.Biol, 2003, 48: 2987-2998. DOI:10.1088/0031-9155/48/18/303 |
| [3] |
Hou Q, Wang J, Chen Y, et al. Beam orientation optimization for IMRT by a hybrid method of the genetic algorithm and the simulated dynamics[J]. Med. Phys, 2003, 30(9): 2360-2367. DOI:10.1118/1.1601911 |
| [4] |
Li YJ, Yao Jonathan, Yao DZ. Automatic beam angle selection in IMRT planning using genetic algorithm[J]. Phys. Med. Biol, 2004, 49: 1915-1932. DOI:10.1088/0031-9155/49/10/007 |
| [5] |
陈超敏, 唐木涛, 周凌宏, 等. 调强放射治疗中剂量计算与参数优化研究[J]. 中华放射医学与防护杂志, 2006, 26(3): 53-55. |
| [6] |
唐木涛, 陈超敏, 周凌宏, 等. 遗传算法优化调强放射治疗射野权重初步研究[J]. 南方医科大学学报(原第一军医大学学报), 2006, 12(4): 456-458. |
| [7] |
唐木涛, 陈超敏, 周凌宏, 等. 遗传算法优化放射治疗计划射野权重的收敛性分析[J]. 医疗卫生装备, 2006, 27(1): 21-22. DOI:10.3969/j.issn.1003-8868.2006.01.010 |
| [8] |
陈超敏, 周凌宏, 唐木涛, 等. 静态调强放射治疗新方法研究[J]. 第一军医大学学报, 2005, 25(12): 1494-1497. DOI:10.3321/j.issn:1673-4254.2005.12.008 |


